Journal of Fluid Flow, Heat and Mass Transfer (JFFHMT)

ISSN: 2368-6111

1. Introduction

Radiative heat transfer in participating media, such as furnace gases, the atmosphere, and clouds, involves absorption, emission, and scattering phenomena [1]. Thermal radiation interacting with a medium leads to energy absorption, reducing transmitted energy, while scattering redirects radiation in multiple directions, causing out-scattering and in-scattering. Scattering can be isotropic or anisotropic, influenced by factors like temperature, composition, and spectral properties. In high-temperature environments like furnaces, combustion byproducts such as carbon dioxide and water vapor significantly affect radiation absorption and scattering, with their properties being spectrally dependent and temperature-sensitive. Additionally, soot further complicates these radiation interactions.

Traditionally, radiative transfer equation (RTE) solvers adopt either physics-based (stochastic) or deterministic methods. Methods like Monte-Carlo [2] excel in parallel computing but face challenges with numerically handling optically thick media and integrating with other physics, such as fluid mechanics. Consequently, researchers often turn to numerical methods that account for the spectral properties of gas species and particulate matter, as well as their interactions within combustion chambers. Methods like this such as finite volume [3] and finite element [4] methods incur significant computational costs, rendering the overall process slow, cumbersome, and expensive. In addition, mesh-based methods (e.g discrete ordinates) are very sensitive to the computational dimension and suffer from the curse of dimensionality, given the high dimensionality of RTE. In order to address these challenges, there is a growing need for RTE models that require fewer computational resources and less time.

In recent computational trends, artificial neural networks (ANNs) are increasingly favoured over elaborate physical models due to their minimal computational requirements [5]. One promising approach involves substituting exhaustive RTE solutions with ANN prediction models in strongly scattering media. ANNs, however, often require large amounts of data and can struggle with generalization, resulting in higher computational costs and less accurate predictions. Recent breakthroughs like physics-informed neural networks (PINNs) show potential for problems governed by partial differential equations [6]. Unlike pure data-driven ANN, PINNs embed differential equations into the training process [7]. These mesh-free models select random discrete points in the computational region (or take data from simulations/experiments), making them less sensitive to dimensionality issues especially in RTE problems [8].

In this study, the one-dimensional radiative transfer equation (RTE) is solved using a Physics-Informed Neural Network (PINN) model. The physical principles of the RTE are integrated into the neural network framework, allowing for efficient handling of the complexities of radiative transfer. The solutions obtained from the PINN model are validated against previous studies, and results are presented in terms of radiation intensity and flux for various extinction coefficients. This work not only enhances the theoretical understanding of the RTE but also suggests a fast and efficient method for solving thermal radiative transfer problems in scattering media, demonstrating the significant potential of PINNs in this domain.

2. Mathematical modelling

2.1 Radiation transport equation (RTE), scattering phase function and boundary conditions

Generalized steady radiation transfer equation (RTE) for a system with participating medium can be written as follows [9].

(1)

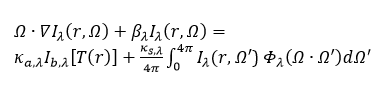
Here, I_λ (r,Ω) is specific intensity of radiation at position 𝑟 in direction Ω and wavelength 𝜆. β_λ is the extinction coefficient at wavelength 𝜆 which accounts for both absorption and scattering. κ_a,λ and κ_s,λ are absorption and scattering coefficients, respectively at wavelength 𝜆. I_b,λ [T(r)] is source term, typically representing the blackbody radiation intensity at temperature 𝑇(𝑟). Φ_λ (Ω∙Ω') is scattering phase function, which describes the angular distribution of scattered radiation. In the left side of Eq. (1), first term represents rate of change of specific radiation intensity due to spatial variation. Second term of LHS represents the extinction term due to absorption and scattering. In the right-hand side of Eq. (1), the first term represents the radiation emission by the medium which can be described by a blackbody at temperature T(r).

The most important term for radiation in scattering medium is the last term at right hand side. This term represents the scattering function that denotes radiation scattering from all directions. This term makes the equation [Eq. (1)] an integro-differential equation. For monochromatic radiation in one-dimensional geometry involving non-absorbing medium, the RTE can be expressed as follows:

(2)

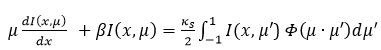
I(x, μ) is the intensity of radiation at position x and in the direction described by the angle cosine μ. μ ranges from -1 (radiation traveling in the opposite direction of the reference axis) to +1 (radiation traveling in the same direction as the reference axis). β is the absorption coefficient of the medium and κ_s is the scattering coefficient of the medium. Φ(𝜇×𝜇′) is the phase function, which describes the angular distribution of scattered radiation. In one-dimension, the scattering phase function can be written as follows.

(3)

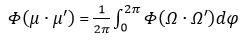
Here, Φ(Ω∙Ω′) is the full phase function depending on the solid angles Ω and Ω′. φ is the azimuthal angle, integrating over 2𝜋 to account for all possible scattering directions in the plane perpendicular to the initial direction. The scattering phase function can be expanded in terms of Legendre Polynomials as follows:

(4)

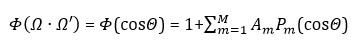
For this problem with one dimension,

(5)

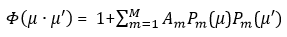
Here, 𝑃𝑚(𝜇) is Legendre Polynomials for the function defined on the interval [−1,1] and Am is the expansion coefficient.

The final form of RTE in terms of Legendre polynomial approximation can be written as follows,

(6)

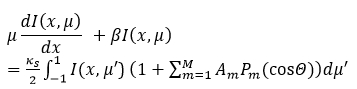
In order to solve Eq. (6), the following boundary conditions are applied.

Incoming radiation intensity: I(0,μ)=1 for μ ∈ (0,1]

Outgoing radiation intensity: I(1,μ)=1 for μ ∈ (-1,0]

2.2. Angular quadrature

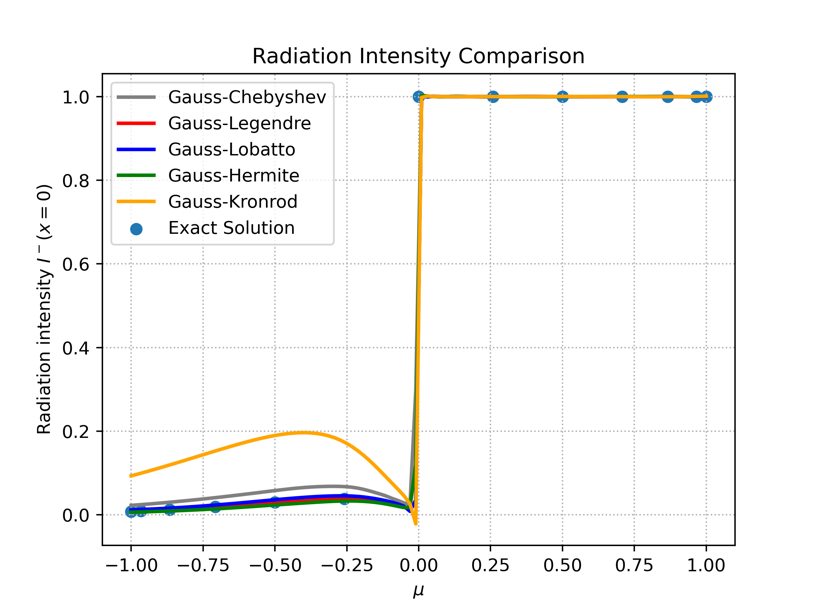
Angular discretization is a key factor that dictates the numerical solution accuracy of radiative heat transfer problems. The selection of a proper angular quadrature is often essential for an efficient solution. In methods like PINN, the computation is significantly affected by angular space quadrature. The solid angular space is two dimensional and described by the zenith angle θ and azimuthal angle φ. For the one-dimensional case, the radiative intensity is only a function of zenith angle θ due to axisymmetry. Five different methods are tested in this work. Gauss–Legendre, Gauss–Labotto, Gauss-Chebyshev, Gauss-Hermite and Gauss-Kronrod are explored based on corresponding quadrature points and weights for integrating over the interval [−1, 1]. These works are compared with an analytical solution scheme [10] as presented in Figure 1. For a quadrature size of 10, Gauss-Legendre method provided better results compared to other methods. Gauss-Legendre quadrature rule takes the following form

(7)

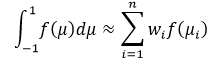
Here, n is the number of sample points used in the approximation; 𝑤𝑖 are the quadrature weights; μ_i are the roots of the i^th Legendre polynomial.

2.3. Training points

As is customary in supervised learning, we need to generate or obtain data to train the network. Generally, experimental or simulation data can be used for detailed PINN studies. In this work, low-discrepancy sequences are considered for training set pertaining to the simplicity of the domain. Interior and boundary collocation points are established with the 1D domain (0< x<1). These data will be the interior training points. These points are needed to be strategically placed to capture the behavior of the system accurately. Each point represents a specific instance in space and intensity.

(a)
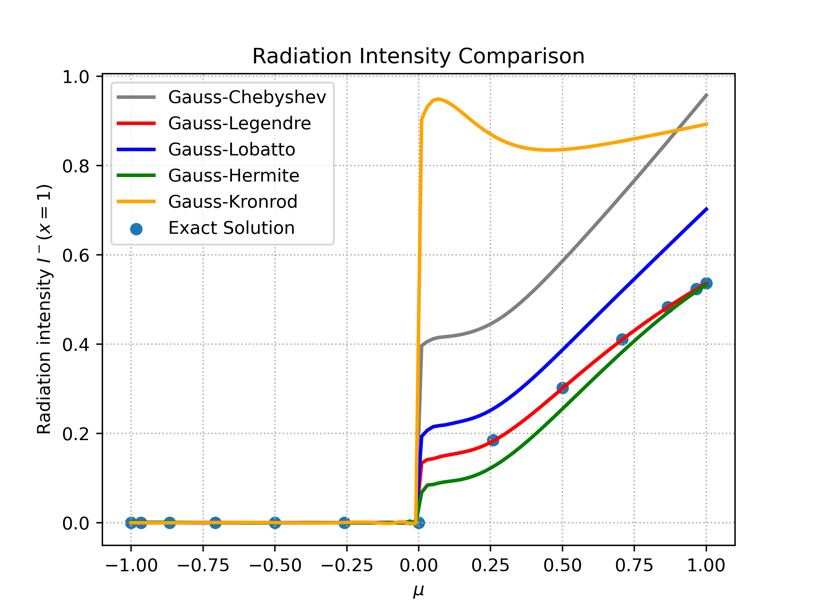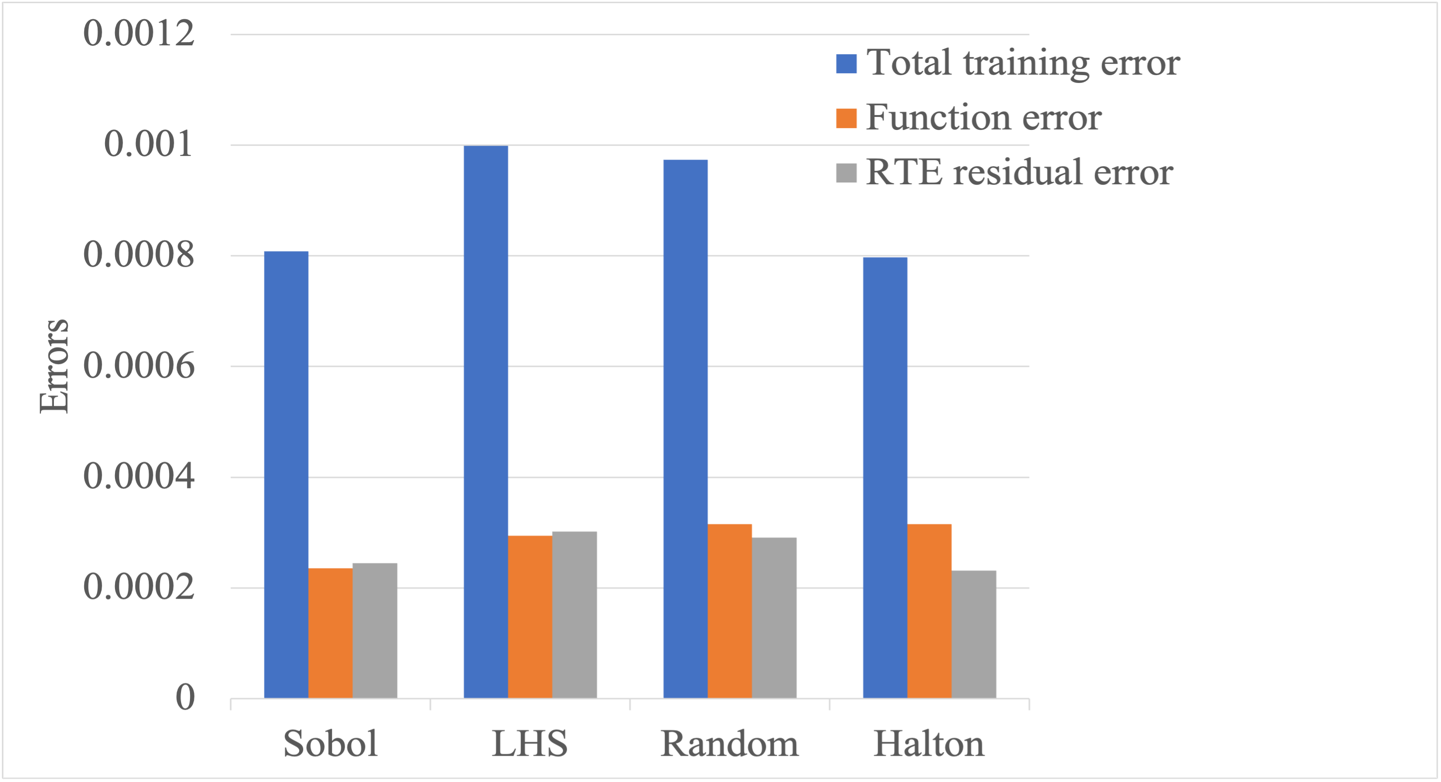
(b)

Different methods are explored to understand the effects on the radiation intensity in the 1D domain. Each sampling method offers a different approach to selecting points within the 1D domain. We focus on sequence sampling method, that involves generating points in a deterministic, ordered sequence. These points are systematically distributed within the domain, ensuring a more uniform coverage. In this work, Sobol, Latin Hypercube Sampling (LHS), random and Halton sequences are considered for tests and the results are shown in Figure 2. For subsequent calculations, Sobol sequence is used.

2.4. Physics informed neural networks (PINNs)

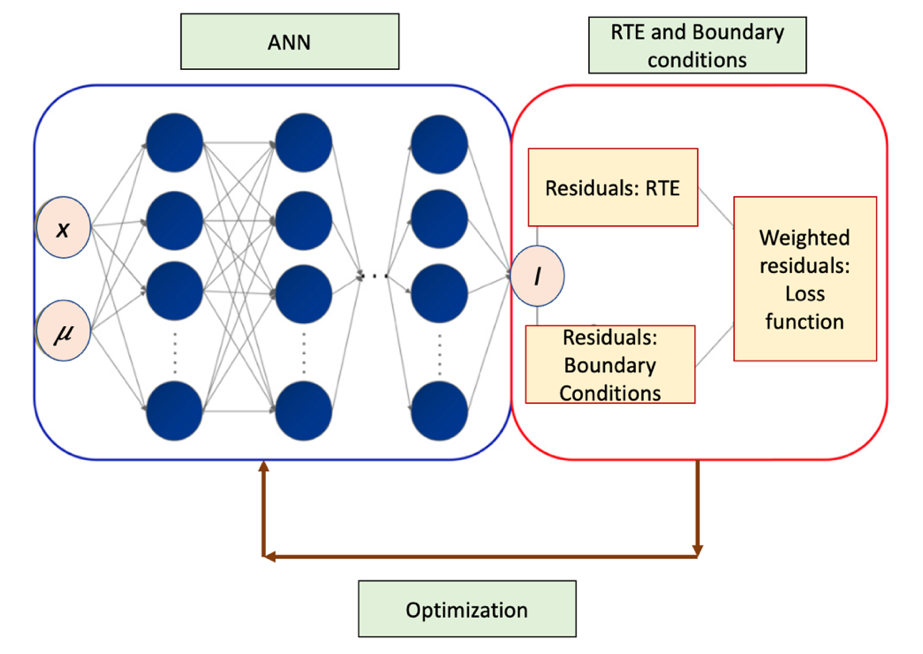
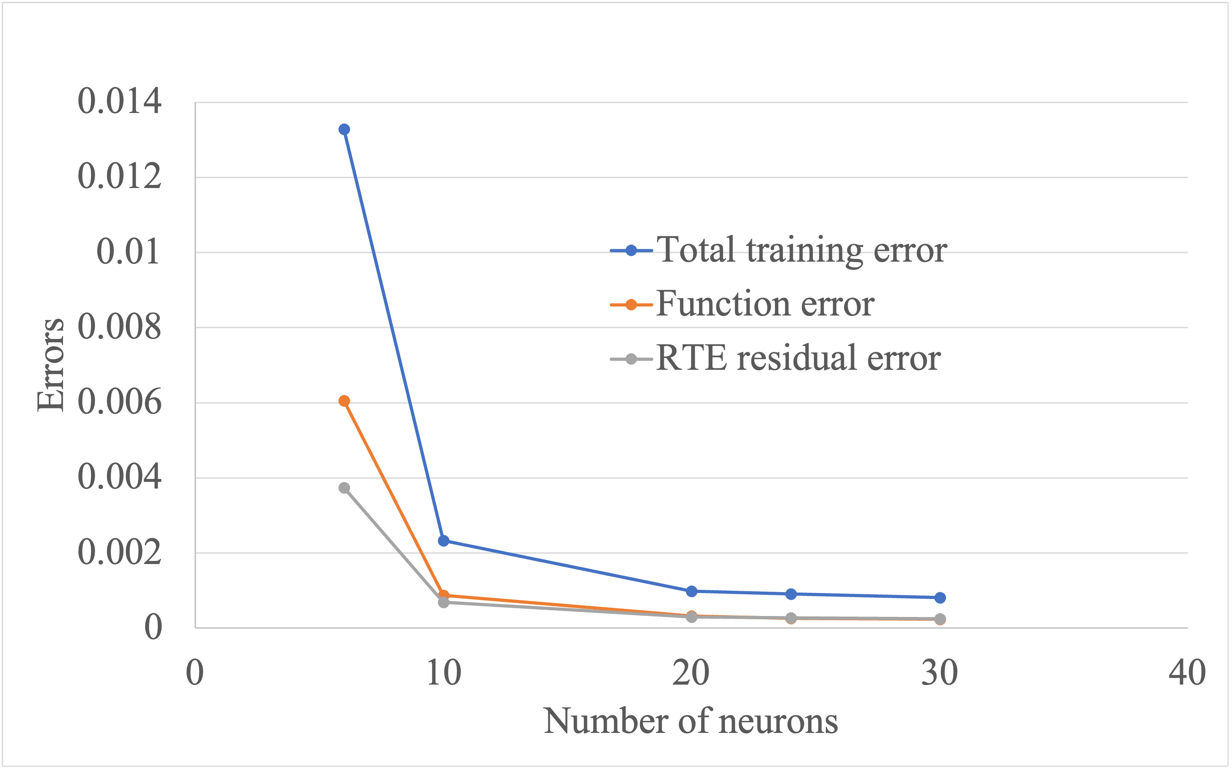
A deep feedforward neural network is used transforming inputs into outputs through multiple layers of neurons. Each layer consists of affine-linear maps and scalar non-linear activation functions. The network has an input layer, an output layer, and multiple hidden layers. In order to solve Eq. (2), the equation is approximated the DNN, which takes spatial (x) and angular (μ) variables as inputs. The outputs the approximated solution Ip , where p denotes the neural network parameters including the weights and biases of neural networks. Figure 3 illustrated the architecture of the PINN. The NN contains two input layers for x and μ. After detailed testing of network hyperparameters, 6 hidden layers with 24 neurons each are considered. Figure 4 shows the effect of hidden layers and neurons on different errors. The tanh activation function is used for all neurons in the hidden layers after comparing with other available activation functions.

The partial differential operator ∂/∂x is implemented by using automatic differentiation using PyTorch. The neural network parameters p are obtained by optimizing the loss function. Loss function includes residual of the RTE and boundary conditions, that makes the neural network dependent on physical governing equations.

(a)
(b)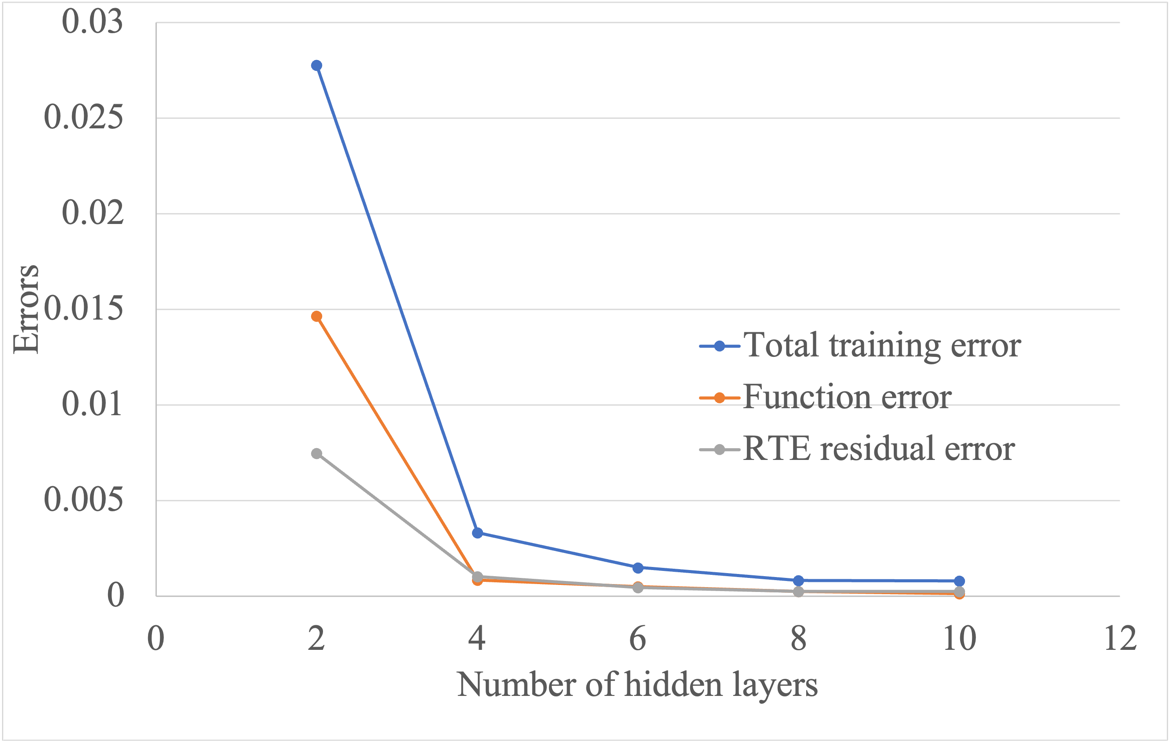

For interior collocation points, the residual is defined as follows:

(8)

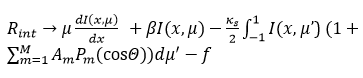
For the boundary conditions, the residuals are

R_bc1→I(1,μ)-1 and
R_bc2→I(0,μ)-0

(9)

The objective is to minimize these residuals simultaneously to determine the weights and biases. The network, RTE residual, boundary residuals, and loss functions are evaluated followed by an optimization algorithm (Adam) to obtain optimal network parameters. The network is trained iteratively, adjusting the weights and biases to minimize the loss function.

3. Benchmark and validation

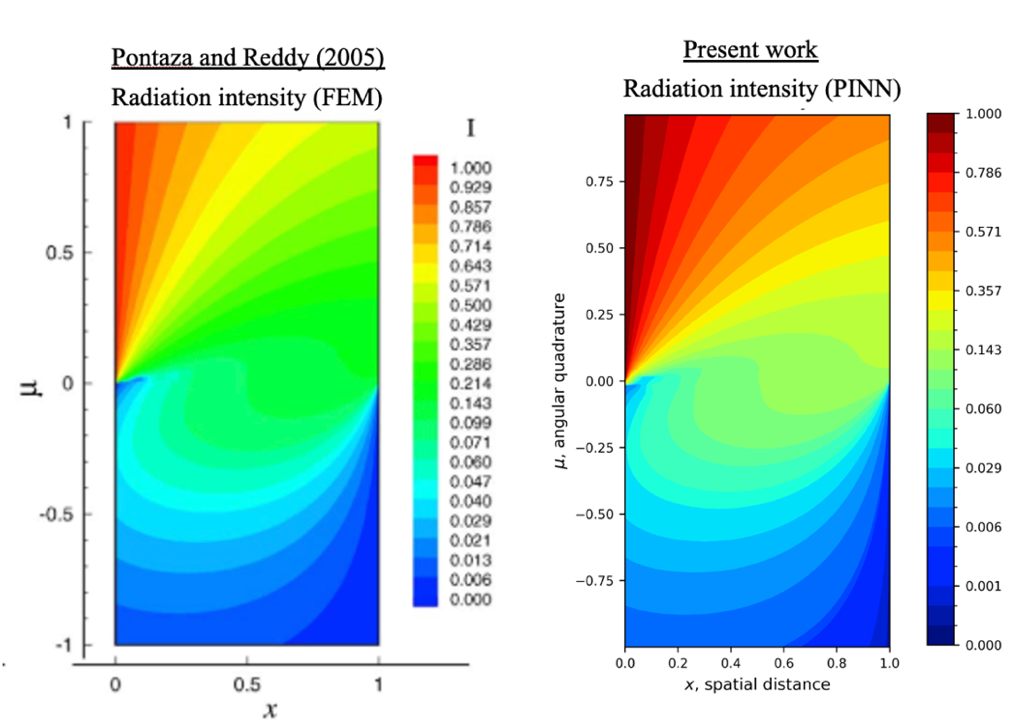
Results from this work are validated with earlier physics based numerical simulation works. Figure 5 shows the comparison of radiation intensity on spatial-angular (μ-x) plane with an earlier work by Pontaza and Reddy [11]. They have carried out 1D simulations for unit thickness using least square (LS) finite element method (FEM). The spatial-angular distributions of the radiation intensity for the current work involving a PINN and the earlier work involving FEM are in excellent agreement.

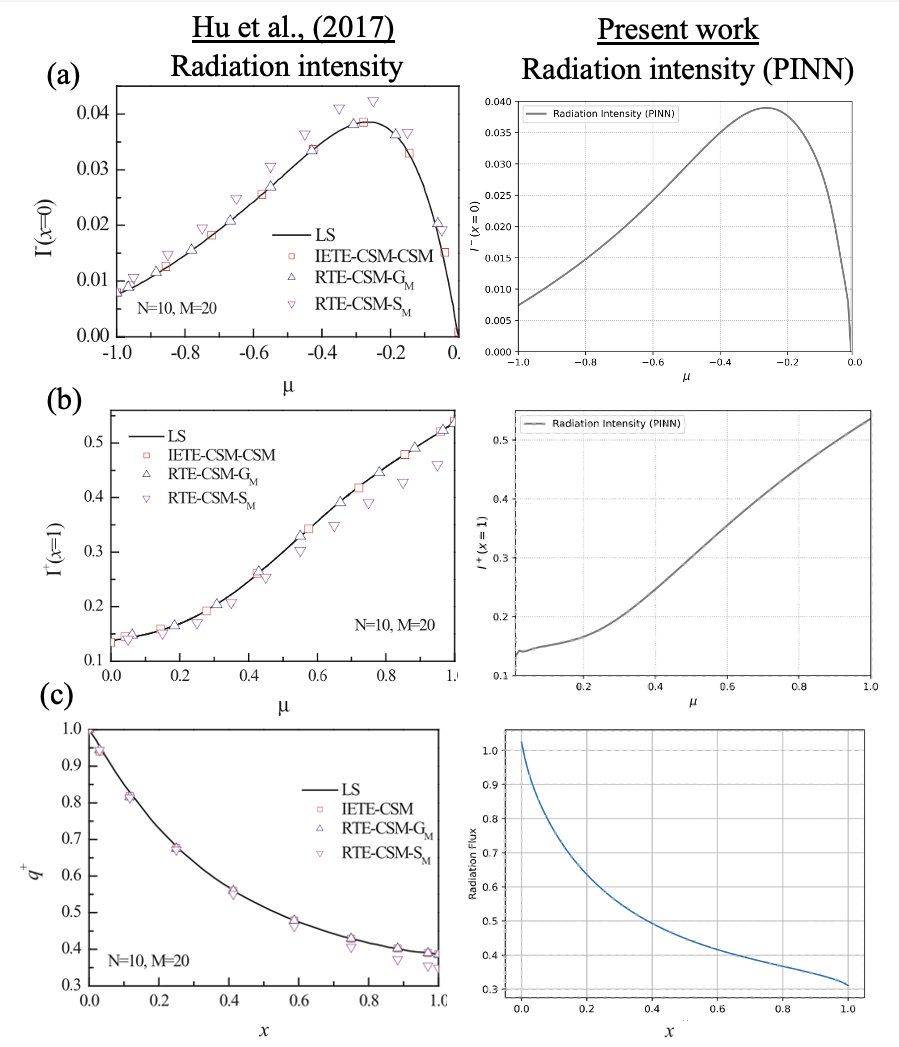
Further validation has been carried out with the detailed work done by Hu et al., [12]. Exit distributions of radiative intensity (I−) at x = 0 and (I+) at x = 1 are plotted in Figure 6 (a) and (b). The results based on different methods angular discretization are in good agreement with slight discrepancy. CSM denotes collocation spectral method. The radiation heat flux is also calculated and compared with the earlier work as seen from Figure 6(c).

4. Results and discussions

In the case of isotropic scattering, a linear space-dependent scattering coefficient, κ_s=x, and unit extinction coefficient, β=1, are considered. The corresponding results are presented earlier with the benchmark results for a unit extinction coefficient. In thermal radiation, the extinction coefficient represents the ability of a medium to absorb and scatter radiation as it passes through. It characterizes how much radiation is absorbed or scattered per unit distance travelled through the material. In combustion, the extinction coefficient represents how radiation interacts with combustion products like gases, soot, and particles. In transparent media like air or water, β tends to be relatively low, reflecting minimal interaction of radiation with the medium. However, in semi-transparent materials such as smoke or steam, β can increase substantially due to higher levels of absorption and scattering by suspended particles or molecules.

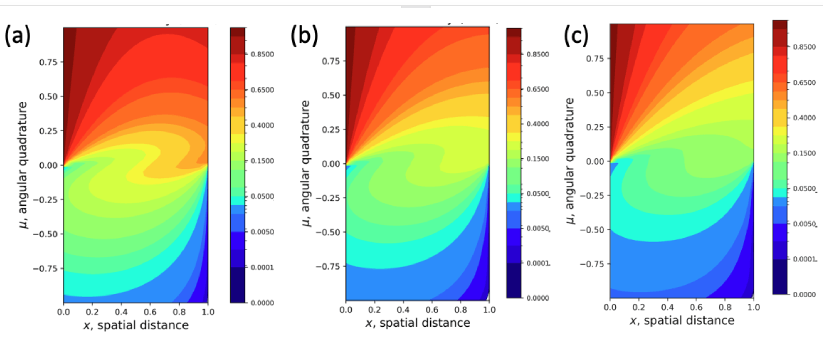
The extinction coefficient contributes to this attenuation by determining the rate at which radiation is absorbed along its path. The effect of the extinction coefficient on radiation intensity with μ at x=0 and x=1 is plotted but not shown to maintain brevity. At lower values of β, radiation intensity is highest as the absorption into the medium is minimal. On the other hand, at larger β values, radiation intensity is minimum as the medium absorbs significant amount of radiation. Common to all cases, radiation intensity decreases exponentially with distance as it passes through a medium due to absorption and scattering processes. A clearer representation with the evolution of radiation intensity on the x-μ plane is presented in Figure 7(a-c). A higher extinction coefficient indicates stronger absorption, resulting in a greater reduction in the intensity of radiation as it penetrates deeper into the medium. This is evident from the lower values of radiation intensity for larger β.

A high extinction coefficient means that the material strongly absorbs thermal radiation, resulting in lower radiation intensity. The material may heat up as it absorbs thermal radiation, leading to a higher temperature gradient across its thickness or volume. If the material cannot efficiently dissipate the absorbed heat, it may accumulate thermal energy, leading to further heating. On the other hand, a low extinction coefficient implies weaker absorption of thermal radiation by the material.

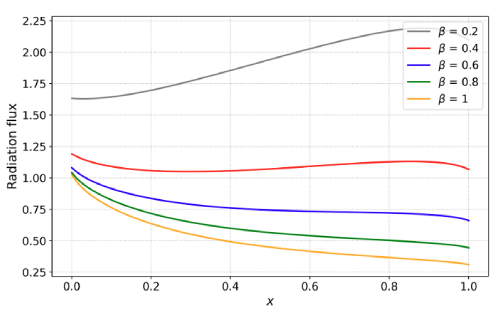
Thermal radiation emitted by a hot object can more readily pass through the material. With less absorption of thermal radiation, the temperature gradient across the material may be more uniform. This nature is clearly illustrated in terms of radiation flux for various β in Figure 8. In environments where thermal radiation plays a significant role, materials with low extinction coefficients may contribute to improved thermal comfort. However, for applications like furnace combustion, control and optimization of the extinction coefficient is necessary.

5. Conclusion

This study focuses on radiative heat transfer in participating media, applicable for various industrial and environmental applications. The solution of radiation transport equation (RTE) based on utilization of a Physics-Informed Neural Network (PINN) model is explored. Through benchmarking and validation against established numerical methods, PINN demonstrated the effectiveness and accuracy for the considered problems. Our future work is focused on 2D and 3D geometries with higher dimensional systems. Detailed investigation into angular quadrature rules and sampling methods are presented. For an isotropic medium, the significance of extinction coefficients on radiation intensity and flux is explained. Findings of this work is pivotal. This study provides a kick-start approach to tackle high dimensionality curse of RTE problems. The fast and reliable PINN based solution provides better theoretical understanding of radiative heat transfer in scattering media.

References