Journal of Fluid Flow, Heat and Mass Transfer (JFFHMT)

ISSN: 2368-6111

Non-Darcian Effects on Natural Convection in a Porous Square Cavity Heated Periodically On Both Sidewalls

Yazan Taamneh^1a, Reyad Omari ^b

^1a Department of Aeronautical Engineering, Jordan University of Science and Technology,
Irbid, Jordan
ymtaamneh@just.edu.jo
^bDepartment of Mathematics, Al-Balqa Applied University, Al-Huson University College,
Irbid, Jordan
reyad.omari@bau.edu.jo

Abstract - The influence of non-Darcian buoyancy on convection caused by buoyancy in a porous square chamber with sine wave boundary conditions on the two sidewalls is examined numerically. A sinusoidal temperature distribution is applied to the cavity's vertical sidewalls. The COMSOL Multiphysics software is utilized to solve the dimensionless governing equations for the porous cavity, which is formulated mathematically using the non-Darcian flow model under local thermal equilibrium. The flow inside the porous chamber is governed by an expanded Darcy model by Brinkman Forchheimer. The simulation results are presented in terms of the Darcy numbers (Da), porosity (ε), phase deviation (ϕ), amplitude ratio (a), Grashof (Gr), and Forchheimer's coefficient (Γ). The heat transfer rate was increased by the amplitude ratio, porosity, Grashof, and Darcy numbers. Moreover, heating both sides of the vertical cavity increases the rate of heat transfer more than heating just one.

Keywords: Porous square cavity, sinusoidal boundary condition, and Darcy flow

© Copyright 2024 Authors - This is an Open Access article published under the Creative Commons Attribution License terms Creative Commons Attribution License terms. Unrestricted use, distribution, and reproduction in any medium are permitted, provided the original work is properly cited.

Date Received: 2024-01-31
Date Revised: 2024-02-29
Date Accepted: 2024-04-23
Date Published: 2024-05-01

1. Introduction

The past few decades have witnessed a continuous interest in heat transfer and fluid flow in enclosures at various thermal boundary conditions due to numerous applications in engineering, such as the operation of solar collectors, the cooling of electronic equipment, hot- and chilled-water storage tanks, furnaces, ovens, and many more. The walls may experience an uneven temperature distribution because of shadowing, the cooling of electrical components, and the absorption of solar energy. Therefore, it is crucial to understand the thermal convection mechanism in an enclosure with a non-uniform temperature distribution.

Lakhal et al. [1] conducted a numerical analysis of transient natural convection heat transfer in a square cavity where the bottom wall was heated at varying temperature over time. According to their findings, they placed the heating element in the middle of the enclosure which showed a great improvement in heat transfer.

Thermal convection in a heated square cavity was studied numerically over time by Kwak and Hyun [2]. They discovered that when the Rayleigh number increases, the resonance phenomenon becomes more noticeable and the Nusselt number is amplified. They concluded that, in the resonant situation, the interior core is impacted significantly by the hot-wall temperature oscillation, and the temperature field there exhibits a periodic tilting of isotherms.

Abourida et al.'s [3] numerical investigation of the natural convection heat transfer in an air-filled square cavity was conducted under various combinations of thermal variable boundary conditions on the cavity's horizontal walls. They found that, for large Rayleigh numbers, periodic heating can be utilized to either significantly lower or slightly increase heat losses in comparison to the constant temperature condition.

Natural convection in a two-dimensional rectangular enclosure with adiabatic conditions on the bottom and sidewalls and a sinusoidal temperature profile on the upper wall was quantitatively studied by Sarris et al. [4]. It was discovered that conduction across the fluid layers dominates heat transfer as Rayleigh numbers increase, and that conduction decreases at very high Rayleigh numbers. Furthermore, it was discovered that when the Rayleigh number increased, the recirculation patterns moved away from one another and toward the matching upper wall corners.

Kalabin et al.'s numerical study [5] investigates the natural convective heat transfer in an inclined square enclosure. It demonstrated how the oscillation frequency and inclination angle depend on the time-averaged heat flux. For the two Grashof numbers under study, 2 ×10⁵ and 3 ×10⁵, it was discovered that the values of inclination angle 54^o and dimensionless frequency f= 20 π correspond to the greatest heat transmission.

The topic of porous cavities under varying temperatures or heat flow boundary conditions has drawn a lot of attention recently, in addition to natural convection in a non-porous cavity with uniform and non-uniform thermal boundaries. Many thermal engineering applications, including heat exchangers, solar collectors, geothermal reservoir water circulation, grain storage, chemical catalytic reactors, and electronics cooling, use porous medium applications [6-7].

Natural convection in a porous chamber with adiabatic vertical walls, hot bottom walls, and cool top walls was investigated in a computational work by Saeid et al. [8]. It was found that as the amplitude of the temperature variation or the length of the heat source increases, the average Nusselt number also increases.

Beckermann et al. [9] performed a numerical analysis of natural convection within a porous medium-filled enclosure. They established the significance of the non-Darcian effects and used the Brinkman-Forchheimer extended Darcy model. For three distinct Darcy number ranges, they offered correlations between Nusselt numbers.

Steady natural convection in a porous cavity with uniform heat generation for a variety of aspect ratios and Rayleigh numbers were quantitatively studied by Du and Bilgen [10]. Natural convection in a porous cavity with variable porosity was examined by Nithiarasu et al. [11]. They noticed that the properties related to heat transfer and flow structure are affected by porosity.

A porous enclosure with a linear temperature distribution on one side wall was studied by Kumar and Singh [12,13]. Later, they studied a porous enclosure with a linear temperature profile and one wavy side wall. For thermal stratification 0 ≤ S ≤1, it was discovered that the highest heat flux is achieved when the wave phase 210o ≤ ø ≤ 240o.

Hossain and Wilson [14] performed a numerical investigation of convective flow in a fluid-saturated porous media in a square enclosure with heat generation. Researchers found that when generation is increased, the enclosure's heated wall's proximity to the vortex and its thermal gradients are both reduced.

Krishna et al. [15] performed a numerical study of natural convection in a porous square cavity with internal heat generation using a generalized non-Darcy technique. They demonstrated how the anisotropic characteristics significantly affect heat transmission and flow dynamics.

The natural convection in a fluid-saturated porous annulus with discontinuous heating was explored statistically by Sankar et al. [16]. They discovered that the flow pattern and rate of heat transmission in the annular cavity are influenced by the heater's size and placement.

Singh et al. [17] investigated the non-Darcian influence on laminar natural convection flow in a vertical channel that is partially filled with a porous material. According to their observations, skin friction at the wall increases when the Darcy number increases, while it decreases when the Grashof number, kinematic viscosity ratio, or porosity increases.

Rahman et al. [18] investigated mixed convection using the finite element method in a rectangular cavity containing a heat-conducting horizontal circular cylinder. Varol et al. [19] conducted a numerical investigation into natural convection for a porous rectangular enclosure with a temperature profile that varies sinusoidally on the bottom wall. As the amplitude grows, so does the heat transmission, and as the aspect ratio increases, it reduces.

Sivasankaran et al. [20] numerically studied natural convection in a porous cavity with sinusoidal heating on both sidewalls. It was discovered that an increase in the amplitude ratio, porosity, and Darcy number resulted in a higher heat transfer rate.

Based on a careful examination of the literature, it appears that the majority of research has been focused on partially heated vertical porous enclosures using Darcy's law as well as fully linearly heated or cooled vertical porous enclosures.

The non-Darcian effect on the flow structure and the associated heat transfer for periodically heated porous enclosures, however, is not well understood. The primary aim of this study is to examine how inertia and viscous forces affect natural convection in a square cavity filled with saturated porous medium for sinusoidal temperature distribution on both side walls. This will be achieved by utilizing the Brinkman-Forchheimer-extended Darcy model. To the best of my knowledge, this problem has never been considered before, so the presented results are novel and unique.

2. Mathematical Analysis

An incompressible, laminar, steady-state natural convection flow inside a square cavity filled with a porous media is investigated. The vertical walls of the cavity on the right and left are subjected to distinct sinusoidal temperature distributions at different phase shifts and amplitude ratios. The horizontal walls at the top and bottom were left insulated.

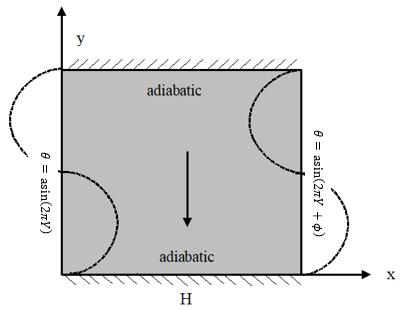
A two-dimensional square cavity of length H is schematically depicted in Figure 1. The two-dimensional flow can be represented in terms of the velocity components in the x and y directions, u and v, respectively.

In the present study, a Brinkman-Forchheimer modified Darcy’s model was used to model the porous medium. On the other hand, it is assumed that the porous medium is isotropic, homogenous, and in thermodynamic equilibrium with the fluid. The physical properties of the solid matrix and the fluid are assumed to be constant except for the buoyancy effects where the Bousinesq approximation is applied to account for the buoyancy force driving the convective motion of the fluid, as described by Ghani et al. [21]. Finally, viscous dissipation is neglected in the energy equation.

The temperature boundary condition subjected to the left and right all of the square cavity is defined as T(y)=T_c and T(y)=Asin(2πy/L+ϕ), respectively here A is the cavity's right wall's sinusoidal temperature amplitude. and ϕ is the phase deviation. Depending on the assumption mentioned above, the governing equations in the dimensionless form are given as:

Continuity:

(1)

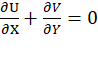
Momentum:

(2)

(3)

Energy:

(4)

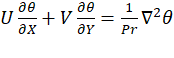
In the equations above, the dimensionless variables are defined as

(5)

The non-dimensional parameters that appeared in the above equation i.e. Grashof, Darcy, and, Prandtl number, are defined as.

(6)

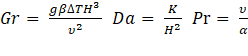
The no-slip condition is imposed for all velocities on the walls, and the dimensionless thermal boundary conditions are as follows.

(7)

(8)

(9)

(10)

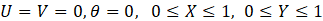
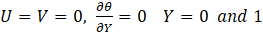
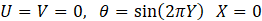
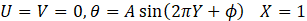
Streamlines are considered the most adequate tools to visualize the fluid flow structure inside a two-dimensional fluid flow, and consequently, the stream functions are defined as.

(11)

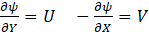
When dealing with heat flux, isotherms are well established as very useful tools to visualize two-dimensional convective heat transfer in an isotropic medium. Therefore, the local Nusselt number along the heated wall of the cavity is given as.

(12)

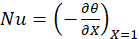
The averaged Nusselt number along the side walls is determined as follows.

(13)

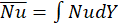
3. Numerical Analysis

The finite element method is used to discretize the governing equations. A central-difference discretization method with second-order accuracy is employed for the momentum equation. An implementation of the QUICK scheme is made to compute the convective terms' third-order value. To solve steady two-dimensional incompressible viscous flows, an implicit finite element approach is proposed. The coupling between the pressure and velocity fields is adopted by using the SIMPLE algorithm. When the nondimensional equations are discretized and integrated over each element, a system of non-linear algebraic equations is obtained. A high number of cells are clustered near the walls of the cavity to compensate for the high-velocity gradient in the boundary layer region of the viscous flow. The adequacy of the grid is verified by comparing the results of different grid sizes. A mesh refinement study was carried out to ensure grid-independent solutions.

The grid independence is performed for Gr = 10⁶, Da = 10⁵, ε = 0.5, and Pr = 1It was discovered that for grid sizes 100×100 and 150×150, the average Nusselt number is almost the same. The numerical solution of the momentum equation formed in a grid was found to be invariant up to 150 grids in the y-direction. Thus, all velocity profiles are obtained using this grid size. An equivalent refinement investigation of the energy equation was carried out. It was found that increasing the number of grids did not affect the results. The simulation terminates when the residuals for the continuity, momentum, and energy equations approach 10-⁶.

4. Results and discussions

In this study, the verification of computer code is crucial. Two test cases are run to verify that the code for the current study is accurate. Firstly, the current computational code is validated by comparing its output with the results of previous studies on natural convection in a porous square cavity [22]. This can be seen in Table 1.

Table 1. Comparison of average Nusselt number for square cavity with Pr = 1.0, Fc = 0.0, Da = 10-2

Nu
	ε = 0.4		ε = 0.9
Ra	Nithiarasu et al. [12]	Present	Nithiarasu et al. [12]	Present
103	1.010	1.008	1.023	1.018
104	1.408	1.40	1.64	1.67
105	2.983	3.16	3.91	4.08
5*105	4.99	5.22	6.70	6.86

First, table 1 shows that the present results are in good agreement with those obtained by Nithiarasu et al. [12] while slight differences appear in the height of Ra. However, it should be noted that much coarser meshes were used in Ref. [12]. Secondly, the present code's output is compared to Deng and Chang [23] finding of natural convection in a non-porous cavity with sinusoidal temperature fluctuation on both walls. The same geometrical and physical parameters are used for the numerical computations, and the outcomes are obtained. The streamlines and isotherms in Figure 2 are compared to the findings of Deng and Chang [23] and demonstrate a strong degree of agreement. These findings give confidence in the current code's accuracy for studying the subject under consideration.

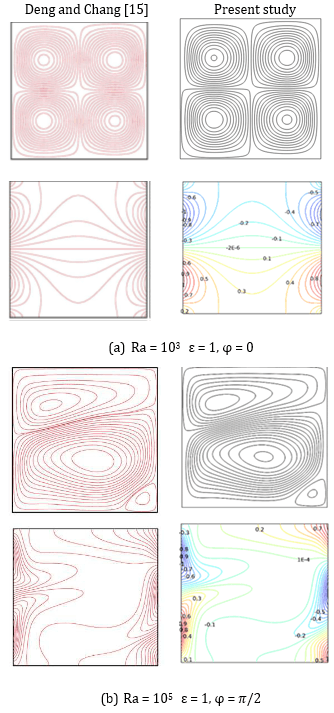
This article demonstrates the impact of sinusoidal boundary conditions on fluid flow and heat transfer using numerical simulations of natural convection in a square porous cavity. Sinusoidal temperature boundary conditions are maintained for the vertical walls on the right and left. The Grashof numbers taken into consideration in this study fall between 10³ and 10⁷. The Darcy number was between 10^-1 and 10^-5. In the current simulation, the angle that is taken into consideration has a phase deviation of ϕ = 0, π/4, π/2, 3π/2 and π. The amplitude ratios that are chosen are a = 0.25, 0.5, 0.75, 1. The Prandtl number, Pr = 1, is kept constant, and the porosity parameter, 0.2 and 0.5, are assumed. The streamlines within the porous cavity are shown in Fig. 3 for two Darcy numbers and different phase deviations.

To simulate the limiting case of viscous flow and Darcy, the values of 10^-5 and 10^-1 were chosen as the Darcy numbers. At low Darcy number i.e. 10^-5, the Brinkmann model reduces to Darcy law. This in turn slows down the convective motion because of the increase of the bulk friction drag induced by the solid matrix.  Nevertheless, as the Darcy number rises from 10^-5 to 10^-1, the influence of viscous forces will become more significant, leading to a progressive decrease in the boundary friction resistance. Fluid circulation is thus greatly enhanced inside the porous cavity.; For Da = 10^-5, ε = 0.5, and ϕ = 0, the flow pattern is made up of two comparable cells inside the porous cavity. The centers of rotation of the flow pattern are located near the right wall of the cavity. It is interesting to note that the cell's structure exhibits a different flow pattern when the Darcy number increases to 10^-1. In this case, the core region of the two vortices shifted slightly to the left of the cavity, and the flow circulation near the left cavity was found to be weak. Moreover, when increasing the phase deviation, the flow pattern changed significantly. Increasing the value of phase deviation up to ϕ = π /4, two major cells occupy the cavity, and a very small cell appears near the right-top corner. Further increasing ϕ to π/2, two similar cells at the right-top and bottom edges are formed and finally, disappear at ϕ = π. It was observed the same effect on the flow structure for Da = 10^-1 and ε = 0.5.

The isotherms for different phase deviations, porosity, and Darcy numbers for a fixed amplitude ratio value are shown in Figure 4. The right and left walls of the cavity contain the isotherms for every value of ϕ. All across the cavity, the isotherms are distributed. According to the isotherms, there is nearly equal heat transfer along each of the sidewalls at amplitude ratio a = 1. When comparing the isotherms for Da = 10^-5 and 10^-1, it can be noted that the convection is stronger for Da = 10^-1 due to the denser thermal boundary layer throughout the right sidewall's heating area. On the other hand, when two temperature distributions vary sinusoidally, both sidewalls are active, which improves heat transfer. It can be noted that when the Darcy number rises from 10^-5 to 10^-1, the heat transmission method may switch from conduction to convection.

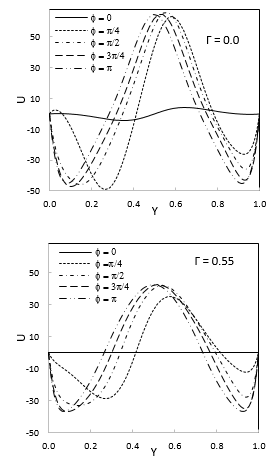
The mid-width profiles are displayed in Figure 5 for a range of Forchheimer and phase deviation values. It is evident from the bi-directional velocity profiles that the cavity's multicellular flow patterns. In comparison to other values of ϕ, the fluid velocity at the cavity's mid-width/ is lower for ϕ = 0. In heat transfer applications, the rate of heat transmission along the heated or cooled surfaces is crucial. For both velocity profiles, the velocity peak values rise as phase deviation grows. It is evident that for Forchheimer number 0.55, the horizontal velocity profile's magnitude is smaller.

For the left and right vertical walls, Figure 6 shows the local Nusselt number for various phase deviations and Forchheimer number. The right sidewall is primarily affected by the phase deviation variation in heat transfer, while the left sidewall is not greatly impacted. The heat transfer is enhanced slightly along the wall when Forchheimer number 0.55.

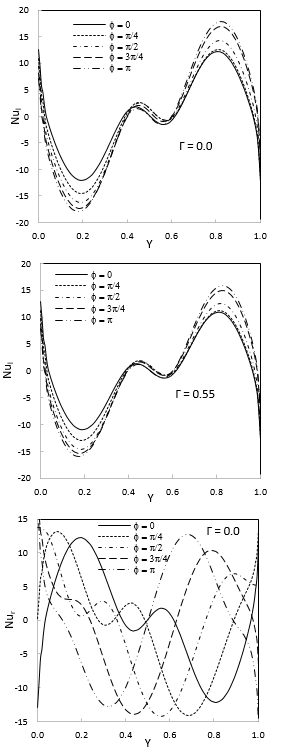
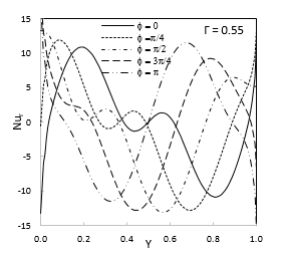
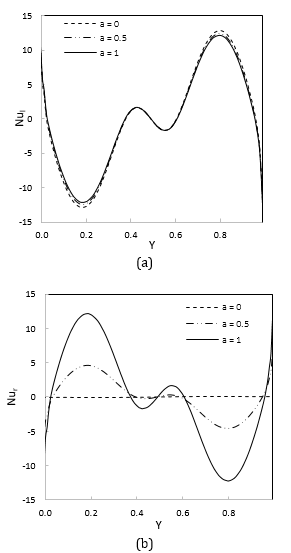
Figure 7 shows the local Nusselt number for the left and right vertical walls at varying amplitude ratios. The local Nusselt number curves make it evident how the boundary temperature affects the rate of heat transfer. Since the right wall remains at a = 0, there is no heat transfer along that wall. Increasing the amplitude ratio for a given value of the other parameters results in an increase in the heat transfer rate along the wall.

One can realize the impact of the overall heat transfer across the cavity by plotting the average Nusselt number against the Darcy and Grashof numbers. Figure 8 displays the average Nusselt number for various phase deviation values. As the Grashoff and Darcy numbers for a given phase deviation increase, the heat transfer rate also increases. With the phase deviation, no detectable tendency is observed. At ϕ = 3π/4, a greater rate of heat transmission is noted for all values of the Grashof number. The rate of heat transfer increases at ϕ = π for all values of the Grashof number when Da ≤ 10-3. Figure 8 shows the average Nusselt number for various amplitude ratios in terms of Darcy and Grashof numbers at ϕ = 0 and ε = 0.5. As the amplitude ratio increases from 0 to 1, it can be observed that the rate of heat transfer increases. Consequently, the right sidewall's sine wave temperature distribution enhances heat transfer profitably.

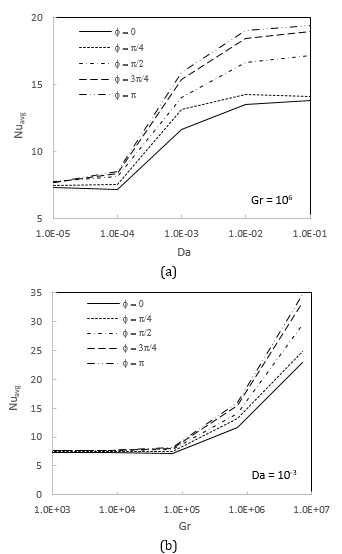
For different amplitude ratios, Figure 9 displays the average Nusselt number versus Darcy and Grashof numbers at ϕ = 0 and ε = 0.5. As the amplitude ratio rises from 0 to 1, the rate of heat transfer increases. This means that, in contrast to the situation of a uniform wall temperature, the nonuniform sinusoidal temperature distribution on the sidewall enhances heat transfer. Additionally, it is noted that the Darcy and Grashof numbers correlate with an increase in the average Nusselt number.

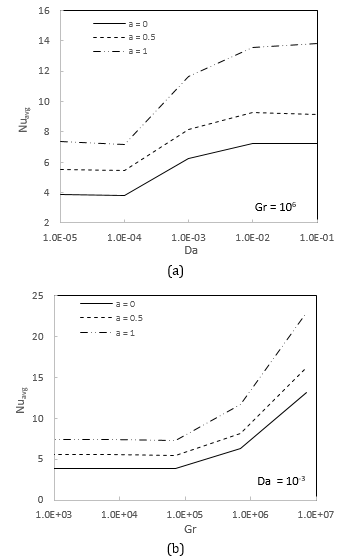
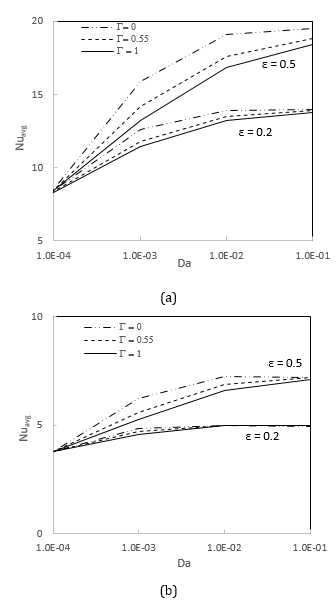
Figure 10 shows the average Nusselt number for two porosity values, as well as the amplitude ratio for various Forchheimer numbers. The rate of heat transfer rises as porosity increases for a given phase deviation and amplitude ratio. In other words, for all values of the Forchheimer numbers, a heat transfer rate is observed unchanged for Da ≤10^-4 and Da ≥10^-1, indicating that the heat transfer rate remains constant regardless of the Forchheimer numbers within this range. Furthermore, an enhancement in the rate of heat transfer is observed with an increase in the amplitude ratio.

5. Conclusion

In this investigation, we conducted a numerical analysis of the phenomenon of steady laminar buoyancy-induced convection within a porous square chamber, where the vertical side walls were subjected to a variable sinusoidal temperature distribution. The primary focus of this study was to explore the influence of key parameters, including the amplitude ratio (a), porosity (ε), Grashof (Gr), Darcy numbers (Da), and phase deviation (ϕ). Our findings indicate a notable enhancement in heat transfer as the amplitude ratio rises from 0.25 to 1. Importantly, the application of a sinusoidal temperature distribution on the left side wall emerges as a profitable strategy for augmenting heat transfer within the cavity. Additionally, we observed that the phase deviation of the sine wave distribution on the left wall exerts a discernible impact on heat transfer within the cavity. It was also found that the phase deviation of the sinusoidal temperature distribution on the left wall affects the heat transfer inside the cavity. Moreover, it was found that the average Nusselt number increases with the porosity and Darcy and Grashof numbers.

Nomenclature

References