Volume 8 - Year 2021 - Pages 244-253
DOI: 10.11159/jffhmt.2021.026

View PDF (Full-text)
Linked References

Analytical Solution of Steady State Heat Transfer In Two Orthotropic Cylinders

Mohammed Nikchi, Hamid Hamza, Khalid Zniber, Jawad Lahjomri and Abdelaziz Oubarra

Laboratory of Mechanics, Faculty of Science Aïn Chock, University Hassan II,
Casablanca 20100, Morocco
mohammed.nikchi-etu@etu.univh2c.ma

Abstract - This paper investigates an analytical solution of 2D steady-state heat conduction in two orthotropic cylinders. The whole lateral surface is subjected to a flux density while the end sections are maintained at prescribed temperatures. The resolution of the problem is carried out analytically by the variable separation technique, taking into account the boundary conditions and the continuity of temperatures and flux at the interface between the two mediums.

The solution expressed in terms of Bessel function showed that ratio of the main thermal conductivities for each medium and the ratio of the radial thermal conductivities of the two mediums have a significant effect on the thermal level in the two mediums as well as on the appearance of the isotherms.

Keywords: Two orthotropic mediums, cylinder geometry, variable separation method, Bessel function, main thermal conductivities, isotherms, axial and radial temperature profiles.

© Copyright 2021 Authors - This is an Open Access article published under the Creative Commons Attribution License terms Creative Commons Attribution License terms. Unrestricted use, distribution, and reproduction in any medium are permitted, provided the original work is properly cited.

Date Received: 2021-09-28
Date Accepted: 2021-10-08
Date Published: 2021-11-05

1. Introduction

Orthotropic multilayer is characteristic of orthotropic materials consisting of several layers. The interest shown in these materials is explained by the very fact that they combine physical, mechanical and thermal properties of various substances. These indicated materials are used in the aerospace [1-3] and heat exchangers [4-5],

The orthotropic materials were investigated in many studies by the analysis of the orthotropic heat conduction equation. F. de Monte [6] present the transient heat conduction problems in one-dimensional multi-layer solids solved by conventional techniques supported Vodicka's approach. Haji-Sheikh et al [7,8] studied the steady thermal behavior of a two-slab 3D body, by the resolution of the steady-state multidirectional heat equation using technique of separate variables. They showed that steady-state solution of a temperature field in a multi-layer body is an invaluable tool for analyzing heat spreaders in electronic cooling applications. This includes heat spreaders with orthotropic or isotropic layers. M. Norouzi et al [9] studies a particular analytical solution for steady conductive heat transfer in multilayer spherical fiber reinforced composite laminates. The orthotropic temperature distribution of laminate is obtained under linear boundary conditions. To get the precise solution, the separation of variables method is employed, and therefore the set of equations associated with the coefficient of Fourier–Legendre series of temperature distribution is solved using the recursive Thomas algorithm.

The notion of layer cylinder is also widely used in investigating the thermal properties of composite materials. Heat transfer in a multilayer cylinder is a problem of significant engineering interest [10,11]. The use of a combination of materials with varying thermal and mechanical properties often helps provide desired performance characteristics for engineering structures. For example, nuclear fuel rods in a nuclear reactor [12], compressed hydrogen storage [13], superconducting cables [14], piezoelectric transducers [15] and civil engineering structures [16].

Several studies have been made in the case of heat transfer in a multilayer cylindrical composite, among others M.H. Kayhani et al [17] who present an analytical solution for warmth conduction in a cylindrical multilayer composite laminate during which the fiber direction may vary between layers. The analytical solution is suitable for various conditions. Ali Keifari Kheibari et al [18] present an analytical solution for the distribution of non-axisymmetric temperature during a long multi-layer cylinder, using the separation of variables method. They studied the effect of fiber angle on the temperature distribution in radial and circumferential directions. H.M. Wang and C.B. Liu [19] Obtained an analytical solution for two-dimensional transient heat conduction during a fiber-reinforced multilayer cylindrical. Separation of variables method is used to develop the transient temperature fields. The presented analytical solution contains trigonometric series and Bessel series, within the polar coordinates, the solving procedure is performed directly in time domain and investigated the effect of the fibers’ angle on the transient heat conduction behaviors.

In the same context of multilayers, the present paper investigated analytically heat conduction in two orthotropic cylinders according longitudinal and radial directions (r , z). The main innovation of the present study is the derivation of the most general analytical solution based on general boundary conditions, which are based on Dirichlet and Newman boundary conditions. For this purpose, we use the variable separation technique, taking into account the boundary conditions and the continuity of the temperatures and flux at the interface between the two mediums. This resolution in dimensionless form, expressed in terms of the Bessel functions, made it possible to apprehend the effect of the study parameters, namely the ratio of the main thermal conductivities for each medium as well as the ratio of the radial thermal conductivities of the two mediums.

2. Problem Formulation and Mathematical Modelling

The study concerns two orthotropic medium in coaxial cylindrical geometry of length L (Figure 1). One of the medium symbolized by A occupies the interior cylinder of radius a , while the second medium B is confined in the annular space limited by the rays a and b . The left and right ends of the two cylinder (z=0 and z= L) are maintained at the same constant temperatures (T0), while the lateral surface (r=b) is subjected to an imposed flux density.

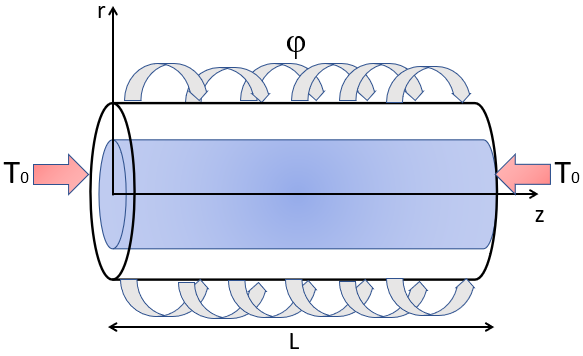
Figure 1. Three-dimensional representation of the two orthotropic cylinders.

Based on the previous assumptions, the equations of the heat diffusion for the two orthotropic mediums are written as:

(1)

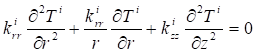
The above equation is applicable respectively for the two orthotropic mediums (i = A and B ). and are the main thermal conductivities along the r , z axes.

The governing differential equations for the temperature distribution are associated to the boundary and interfaces equations:

           
(2)

           
(3)

           
(4)

           
(5)

           
(6)

           
(7)

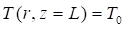
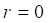
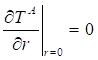
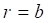
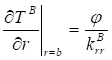
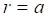
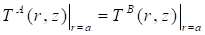
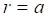
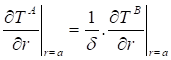
Where, .

The above equations (1)-(7) can be cast in dimensionless form (9)-(15) by incorporating the dimensionless parameters (8):

(8)

Where, .

(9)

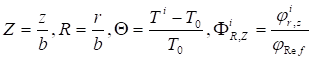
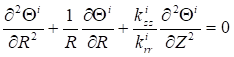
Where, the main thermal conductivities ratio is supposed the same for the two mediums in the study of this problem. It will be expressed simply by .

:           
(10)

:           
(11)

:           
(12)

:           
(13)

:           
(14)

:           
(15)

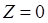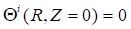
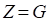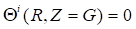
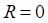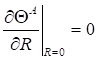
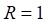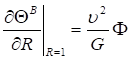
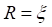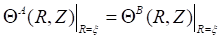
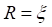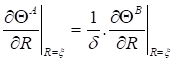
Where, .

Solving the above equations system provides access to the temperature profile in the two mediums according to the Z and R directions cylindrical coordinates.

3. Analytical Solution

The resolution of the problem is carried out analytically by the variable separation technique, taking into account the boundary conditions and the continuity of the temperatures and flux at the interface between the two mediums.

The first step is the use of the boundary conditions (equations 10-13), leading to an intermediate solution of the dimensionless temperatures of medium A and B in the following forms:

(16)

(17)

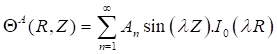
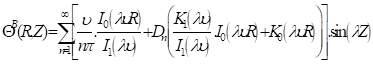
Where, and

I0 , I1: Are Bessel functions of the first kind respectively of order 0 and 1.

K0 , K1: Bessel functions of the second kind respectively of order 0 and 1.

The problem constants An and Dn are determined by the condition of continuity of the temperature and the flux at the interface (equations 14 and 15). This makes it possible to establish the final expressions of dimensionless temperatures of medium A and B in the following forms:

(18)

(19)

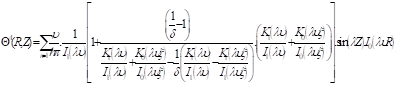
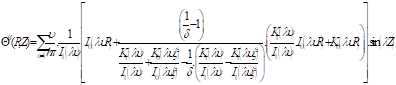
The temperatures within each medium defined by equations 18 and 19 are determined according to an iterative calculation, by comparing the successive all inside temperatures difference between two serial order n and n+1 with a criterion of convergence , according to :

(20)

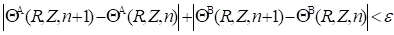
4. Problem Data

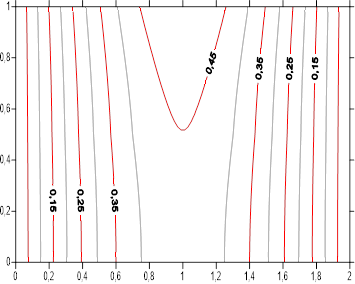
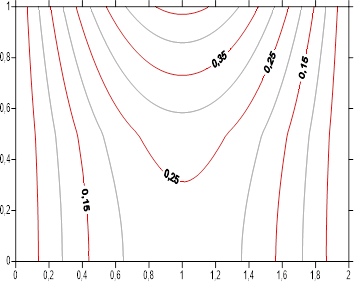
The study is conducted for two orthotropic mediums in cylindrical geometry supposed of a form factor G=2 , submitted to a sinusoidal flux () on the lateral surface. The mediums are characterized by main thermal conductivities according the axial and radial direction. The effect of these parameters is represented by the values of radial thermal conductivities ratio of the two mediums, , taking values equal to 0.5, 1, 2 and by the ratio between axial and radial conductivity equal to 0.25, 1, 4. The orthotropic mediums have a symmetrical configuration in term of axial boundary conditions . Interface location between the mediums is taking equal to .

5. Results and Discussion

Figures [2-10] show the steady state radial and axial temperature within the two mediums for the various values of the study parameters. For each figure, we have simultaneously the domains associated to the A and B mediums separated by the interface characterized by . .

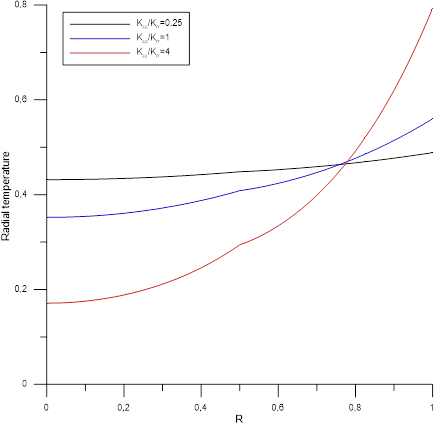
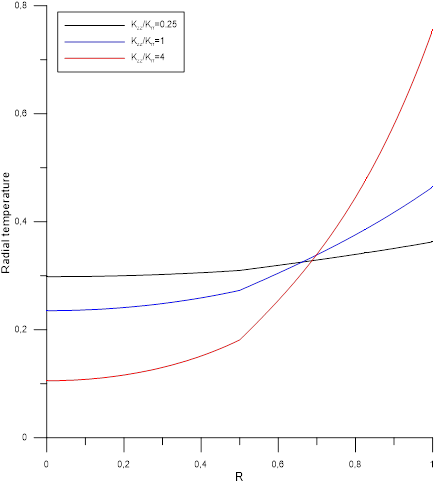
Figures [2-4] present the radial temperature profile in the two mediums middle according to a given value of radial thermal conductivities ratio associated to various values of the main thermal conductivities . Thus, for a fixed value of , the radial temperature profile increases from the center to the outer lateral surface cylinder. Increase of main thermal conductivities ratio reduces thermal level in medium A and increase that in medium B . In addition, we notice that for a given value of main thermal conductivities ratio , the increase of leads to the same conclusions with an overall reduction in the thermal level. Overall, it appears that medium B is more sensitive to the effect of . In addition, we notice a particular radius corresponding to inversion of the medium B temperature with respect to . This particular radius decreases by increasing .

Figure 2. Middle radial temperature for
Figure 3. Middle radial temperature for
Figure 4. Middle radial temperature for

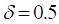
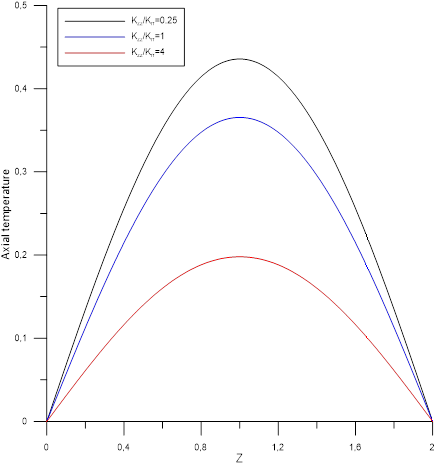
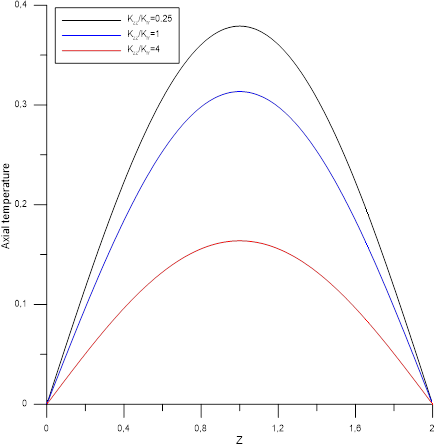
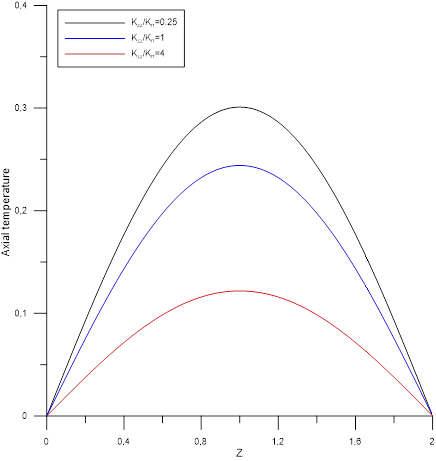
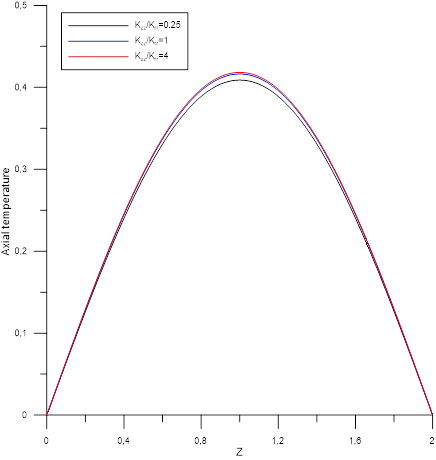
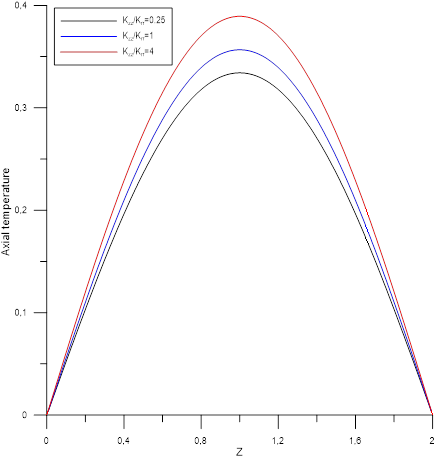
Figures [5-10] shows the axial temperature profile at mid-height of the two mediums respectively and according to the study parameters. Taking into account the sections boundary conditions , the axial profiles temperature for the two medium are symmetrical and depend on the values of the ratio of the main thermal conductivities and the ratio of the radial thermal conductivities . These parameters have the same effect on the internal medium A. Their increases reduce its thermal level. However, the effect of and consequently of axial conduction with respect to radial conduction is most noticeable. With regard to medium , the impact is less significant compared to internal medium. The effect of the ratio only becomes appreciable at high axial conductivity.

Figure 5. Axial temperature at mid-height of medium A for
Figure 6. Axial temperature at mid-height of medium A for
Figure 7. Axial temperature at mid-height of medium for A for
Figure 8. Axial temperature at mid-height of medium B for
Figure 9. Axial temperature at mid-height of medium B for
Figure 10. Axial temperature at mid-height of medium B for

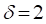
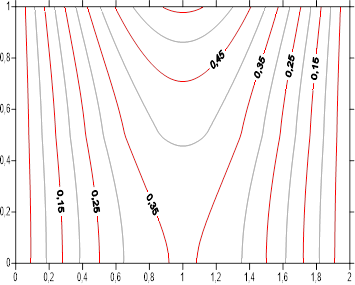
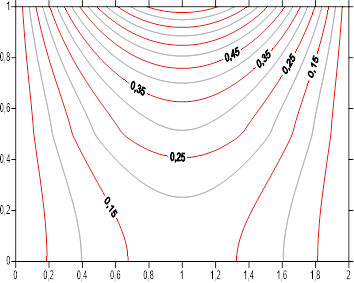
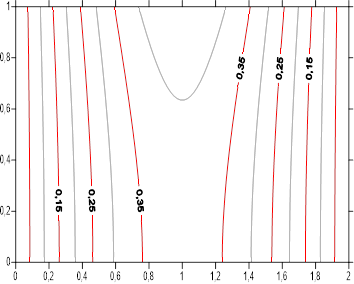
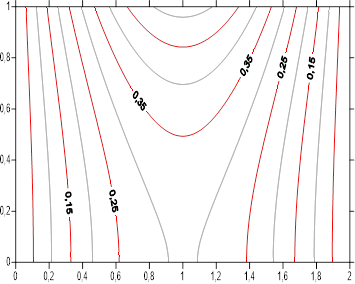
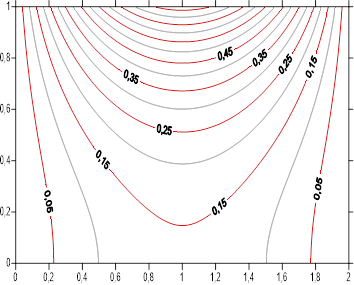
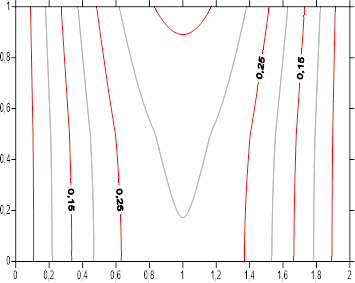
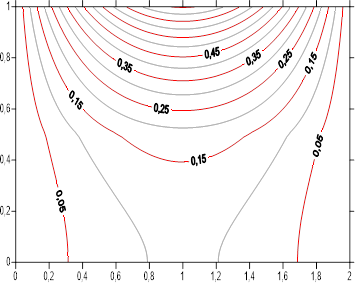
The Figures [11-19] summarize the axial and radial temperature profiles by the steady state isotherms within the two mediums according to study parameters. For each figure, we have simultaneously the domains associated to the and mediums separated by the interface characterized by . For all the figures we note isothermal symmetry according to boundary conditions. Isotherms thermal levels are higher in the middle of lateral surface, subjected to a sinusoidal density flux. Two intermediates cases are present (the mediums became isotropic), and (The mediums have the same radial conductivities). For simultaneously and , the two mediums are reduced to a single one. Apart from these intermediates configurations, isothermal profile has two aspects. For low value of corresponding to weak mediums axial conductivities, isotherms are parallel to cylinder sections except in the center, where the shape of the isotherms translates the heat sinusoidal flux applied to the outer surface. The increase of radial conductivities ratio , that is to say increasing radial conductivity of medium A , reduce thermal level of temperature inside the two medium and make the isothermal profiles less tight. For high medium axial conductivities , thermal level of the isotherms is higher than before. The isotherms are practically circular inside medium B and penetrate advantage inside the second medium A , while being more and more spaced. Effect of radial conductivities ratio is not changed.

Figure 11. Isotherms for and
Figure 12. Isotherms for and
Figure 13. Isotherms for and
Figure 14. Isotherms for and
Figure 15. Isotherms for and
Figure 16. Isotherms for and
Figure 17. Isotherms for and
Figure 18. Isotherms for and
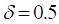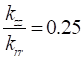
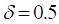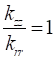
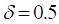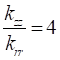
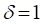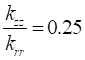
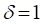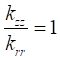
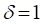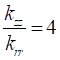
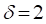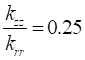
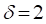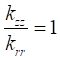
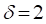Figure 19. Isotherms for and

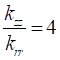
6. Conclusion

The work carried out relates to the analytical determination of the temperature field in two-dimensional steady-state orthotropic mediums. The cylindrical geometry is such that the lateral surface is subjected to a flux density while the sections are isothermal. The results show that ratio of the main thermal conductivities for each medium and the ratio of the radial thermal conductivities of the two mediums affect considerably the isotherms profiles as well the mediums thermal level. Low temperature values correspond to an axial thermal conductivity greater than that of the radial one, or to a radial internal medium conductivity higher than that of the external medium.


References

[1] W. Krenkel, F. Berndt, C/C–SiC composites for space applications and advanced friction systems, Mater. Sci. Eng., A 412 (2005) 177-181. View Article

[2] J. Jedidi, F. Jacquemin, A. Vautrin, Design of accelerated hygrothermal cycles on polymer matrix composites in the case of a supersonic aircraft, Compos. Struct. 68 (2005) 429-437. View Article

[3] C.J. von Klemperer, D. Maharaj, Composite electromagnetic interference shielding materials for aerospace applications, Compos. Struct. 91 (2009) 467-472. View Article

[4] Y. Xia, A.M. Jacobi, An exact solution to steady heat conduction in a two dimensional slab on a one-dimensional fin: Application to frosted heat exchangers, Int. J. Heat Mass Transfer 47 (2004) 3317-3326. View Article

[5] X. Fang, Z. Zhang, Z. Chen, Study on preparation of montmorillonite-based composite phase change materials and their applications in thermal storage building materials, Energy Convers. Manage. 49 (2008) 718-723. View Article

[6] F. deMonte, «An analytic approach to the unsteady heat conduction processes in one-dimensional composite media», International Journal of Heat and Mass Transfer, p. 11, 2002. View Article

[7] A.Haji-Sheikh, J.V. Beck, D. Agonafer, Steady-state heat conduction in multi-layer bodies, Int. J. Heat Mass Transfer 46(2003) 2363-2379. View Article

[8] A. Haji-Sheikh, J.V. Beck, D. Agonafer, Temperature solution in multidimensional multi-layer bodies, Int. J. Heat Mass Transfer 45 (2002) 1865-1877. View Article

[9] M. Norouzi, «A general exact solution for heat conduction in multilayer spherical composite laminates», Composite Structures, p. 8, 2013. View Article

[10] D.W. Hahn, M.N. ¨Ozis¸ik, Heat Conduction, 3rd. Ed., John Wiley & Sons, 2012. View Article

[11] S. Kakaç, Y. Yener, Heat Conduction, 2nd. Ed., Hemisphere Press, 1985.

[12] H. French, Heat Transfer and Fluid Flow in Nuclear Systems, ’ first ed., Pergamon Press, 1981.

[13] S. Manahan, Environmental Chemistry, ninth ed., CRC Press, 2010.

[14] S. Olsen, C. Traeholt, A. Kuhle, O. Tonnesen, M. Daumling, J. Oestergaard, Loss and inductance investigations in a 4-layer superconducting prototype cable conductor, IEEE Trans. Appl. Supercond. 9 (1999) 833–836. View Article

[15] J. Wang, L. Qin, W. Li, W. Song, Parametric analysis and optimization of radially layered cylindrical piezoceramic/epoxy composite transducers, Micromachines 9 (2018), 585:1-16. View Article

[16] M. Cavalcante, S. Marques, M.-J. Pindera, Transient thermomechanical analysis of a layered cylinder by the parametric finite-volume theory, J. Therm. Stresses 32 (2008) 112–134. View Article

[17] H. Kayhani, M. Norouzi, A. Amiri Delouei, Int. J. of Thermal Sciences 52 (2012) 73-82. View Article

[18] A. K. Kheibari, M. Jafari, et M. B. Nazari, «Propagation of heat wave in composite cylinder using Cattaneo- Vernotte theory», International Journal of Heat and Mass Transfer, vol. 160, p. 120208, oct. 2020, doi: 10.1016/j.ijheatmasstransfer. 2020.120208. View Article

19] H. M. Wang et C. B. Liu, «Analytical solution of two-dimensional transient heat conduction in fiber-reinforced cylindrical composites», International Journal of Thermal Sciences, vol. 69, p. 43‑52, juill. 2013, doi: 10.1016/j.ijthermalsci. 2013.02.001. View Article