Volume 3 - Year 2016 - Pages 17-24
DOI: 10.11159/jffhmt.2016.003
Unsteady Stagnation-point Flow of a Second-grade Fluid
Fotini Labropulu1, Daiming Li2
1Luther College/University of Regina
Regina, SK, Canada S4S 0A2
fotini.labropulu@uregina.ca
2Department of Chemical and Petroleum Engineering, University of Calgary
2500 University Dr. NW, Calgary, Alberta, Canada T2N 1N4
Abstract - The unsteady two-dimensional
stagnation point flow of second-grade fluid impinging on an infinite plate is
examined and solutions are obtained. It is assumed that the infinite plate at ![]() is oscillating with velocity
is oscillating with velocity ![]() , the fluid occupies the entire upper half plane
, the fluid occupies the entire upper half plane ![]() and it impinges obliquely on the
plate. The governing partial differential equations are reduced to a system of
ordinary differential equations by assuming a form of the streamfunction a
priori. The resulting equations are, then, solved numerically using a shooting
method for various values of the Weissenberg number,
and it impinges obliquely on the
plate. The governing partial differential equations are reduced to a system of
ordinary differential equations by assuming a form of the streamfunction a
priori. The resulting equations are, then, solved numerically using a shooting
method for various values of the Weissenberg number, ![]() . It is observed that the effect of
the Weissenberg number is to decrease the velocity near the wall as it
increases. Furthermore, analytical solutions are obtained for small and large
values of frequency.
. It is observed that the effect of
the Weissenberg number is to decrease the velocity near the wall as it
increases. Furthermore, analytical solutions are obtained for small and large
values of frequency.
Keywords: Unsteady, Stagnation-point, Oscillating plate, Non-Newtonian fluid
© Copyright 2016 Authors - This is an Open Access article published under the Creative Commons Attribution License terms Creative Commons Attribution License terms. Unrestricted use, distribution, and reproduction in any medium are permitted, provided the original work is properly cited.
Date Received: 2015-09-04
Date Accepted: 2016-01-26
Date Published: 2016-03-17
Nomenclature
|
|
1st and 2nd Rivlin Ericksen tensors |
|
|
similarity variables |
|
|
constant |
|
|
fluid pressure |
|
|
Cauchy Stress Tensor |
|
|
velocity vector |
|
|
velocity
components along |
|
|
constant |
|
|
Weissenberg number |
|
Greek Symbols |
|
|
|
viscoelastic parameters of the fluid |
|
|
frequency |
|
|
constant |
|
|
constant |
|
|
non-dimensional varable |
|
|
fluid viscosity |
|
|
kinematic viscosity |
|
|
Shear stress component |
|
|
non-dimensional variable |
|
|
streamfunction |
|
|
frequency |
1. Introduction
In the past, the fluid flow near a stagnation point has been investigated extensively. Hiemenz [1] derived an exact solution of the steady flow of a Newtonian fluid impinging orthogonally on an infinite flat plate. Stuart [2], Tamada [3] and Dorrepaal [4] independently investigated the solutions of a stagnation point flow when the fluid impinges obliquely on the plate. Beard and Walters [5] used boundary-layer equations to study two-dimensional flow near a stagnation point of a viscoelastic fluid. Dorrepaal et al [6] investigated the behaviour of a viscoelastic fluid impinging on a flat rigid wall at an arbitrary angle of incidence. Labropulu et al [7] studied the oblique flow of a viscoelastic fluid impinging on a porous wall with suction or blowing.
Unsteady stagnation point flow of a Newtonian fluid has also been studied extensively. Rott [8] and Glauert [9] studied the stagnation point flow of a Newtonian fluid when the plate performs harmonic oscillations in its own plane. Srivastava [10] investigated the same problem for a non-Newtonian second grade fluid using the Karman-Pohlhausen method [11] to solve the resulting equations. Labropulu et al [12] used series methods to solve the unsteady stagnation point flow of a Walters' B' fluid impinging on an oscillating flat plate. Matunobu [13, 14] and Kawaguti and Hamano [15] examined the fundamental character of the unsteady flow near a stagnation point for a Newtonian fluid. Takemitsu and Matunobu [16] studied the oblique stagnation point flow for a Newtonian fluid and obtained the general features of a periodic stagnation point flow. The case when the stagnation point fluctuates along a solid boundary is especially interesting from the biomechanical point of view. This is because the wall shear stress experienced by blood vessels may be thought to be increased by pulsating blood flow near the mean position of fluctuating stagnation point [15, 17] and lead to vascular diseases [18].
In
this work, the unsteady stagnation point flow of a viscoelastic second-grade
fluid is examined and solutions are obtained. We assume that the infinite plate
at ![]() is oscillating with velocity
is oscillating with velocity ![]() , the fluid occupies the entire
upper half plane
, the fluid occupies the entire
upper half plane ![]() and the fluid impinges obliquely on
the plate. The governing partial differential equations are reduced to a system
of ordinary differential equations by assuming a form of the streamfunction a
priori. The resulting equations are, then, solved numerically using a shooting
method for various values of the Weissenberg number,
and the fluid impinges obliquely on
the plate. The governing partial differential equations are reduced to a system
of ordinary differential equations by assuming a form of the streamfunction a
priori. The resulting equations are, then, solved numerically using a shooting
method for various values of the Weissenberg number, ![]() . It is observed that the effect of
the Weissenberg number is to decrease the velocity near the wall as it
increases. Furthermore, analytical solutions are obtained for small and large
values of frequency.
. It is observed that the effect of
the Weissenberg number is to decrease the velocity near the wall as it
increases. Furthermore, analytical solutions are obtained for small and large
values of frequency.
2. Flow Equations
The flow of a viscous incompressible non-Newtonian second-grade fluid, neglecting thermal effects and body forces, is governed by
when the
constitutive equation for the Cauchy stress tensor ![]() which
describes second-grade fluid given by Rivlin and Ericksen [19] is
which
describes second-grade fluid given by Rivlin and Ericksen [19] is
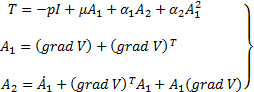
Here ![]() is the velocity vector field,
is the velocity vector field, ![]() the fluid pressure function,
the fluid pressure function, ![]() the constant fluid density,
the constant fluid density, ![]() the
constant coefficient of viscosity and
the
constant coefficient of viscosity and ![]() the normal stress moduli. Dunn and
Fosdick [20] and Dunn and Rajagopal [21] have shown that if the second-grade
fluid described by (3) is to undergo motions which are compatible with
Clausius-Duhem inequality [22] and the assumption that the free energy density
of the fluid be locally at rest, then the material constants must satisfy the
following restrictions:
the normal stress moduli. Dunn and
Fosdick [20] and Dunn and Rajagopal [21] have shown that if the second-grade
fluid described by (3) is to undergo motions which are compatible with
Clausius-Duhem inequality [22] and the assumption that the free energy density
of the fluid be locally at rest, then the material constants must satisfy the
following restrictions:
Considering the flow to be plane, we take ![]() and
and ![]() so that the flow equations (1) to
(3) take the form
so that the flow equations (1) to
(3) take the form
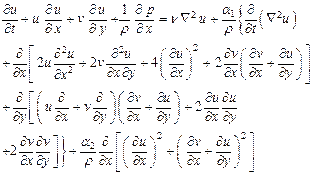
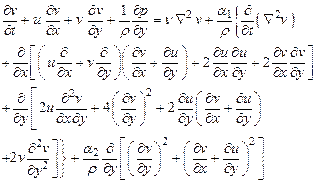
where ![]() is the kinematic viscosity.
is the kinematic viscosity.
Continuity
equation (5) implies the existence of a streamfunction ![]() such
that
such
that
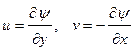
Substitution of (8) in
equations (6) and (7) and elimination of pressure from the resulting equations
using ![]() yields
yields
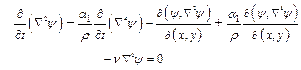
Having obtained a solution of equation (9), the velocity components are given by (8) and the pressure can be found by integrating equations (6) and (7).
The shear stress component ![]() of the Cauchy stress
of the Cauchy stress ![]() is given by
is given by
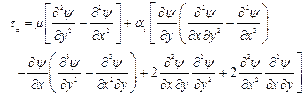
3. Solutions in the Fixed Frame of Reference
Following Takemitsu and Matunobu [16], we assume that
We assume that the infinite plate at ![]() is oscillating with velocity
is oscillating with velocity ![]() and that the fluid occupies the entire upper
half plane
and that the fluid occupies the entire upper
half plane ![]() Furthermore, we assume the streamfunction far
from the wall is given by
Furthermore, we assume the streamfunction far
from the wall is given by ![]() (see Stewart [2]). Thus, the boundary
conditions are given by
(see Stewart [2]). Thus, the boundary
conditions are given by
where ![]() is a
non-dimensional constant characterizing the obliqueness of oncoming flow. It is
assumed that only the real part of a complex quantity has its physical meaning.
is a
non-dimensional constant characterizing the obliqueness of oncoming flow. It is
assumed that only the real part of a complex quantity has its physical meaning.
Substitution of equation (11) in (9) yields
and
Integrating equations (13) and (14) once with
respect to ![]() using the conditions
at infinity, we have
using the conditions
at infinity, we have
and
Using the non-dimensional variables
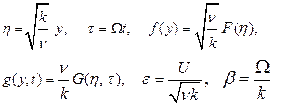
in equations (15) and (16), and boundary conditions (12a) and (12b), we obtain
and
where ![]() is the Weissenberg number.
is the Weissenberg number.
System (18 a-b) has been solved numerically by Garg and Rajagopal [23] and Ariel [24, 25]. Following Bellman and Kalaba [26] and Garg and Rajagopal [23], the quasi-linearized form of equation (18a) is
where the subscript ![]() and
and ![]() represents the
represents the ![]() and
and ![]() approximation to the solution. Since the above
equation is non-homogeneous, the solution at any approximation level can be
written as
approximation to the solution. Since the above
equation is non-homogeneous, the solution at any approximation level can be
written as ![]() . Further, the homogeneous solution,
. Further, the homogeneous solution, ![]() , is a linear combination of two linearly independent
solutions – namely
, is a linear combination of two linearly independent
solutions – namely ![]() and
and ![]() . The details of this technique are well
described by Garg and Rajagopal [23].
. The details of this technique are well
described by Garg and Rajagopal [23].
Using
the quasi-linearization technique described by Garg and Rajagopal [23], we find
that ![]() when
when ![]() . This value is in good agreement
with the value obtained by Takemitsu and Matunobu [16]. Numerical values of
. This value is in good agreement
with the value obtained by Takemitsu and Matunobu [16]. Numerical values of ![]() for different values of
for different values of ![]() are shown in Table 1. These values
are in good agreement with the values obtained by Garg and Rajagopal [23] and
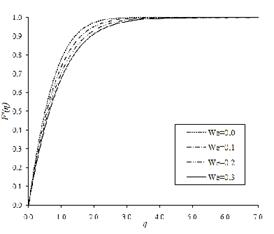
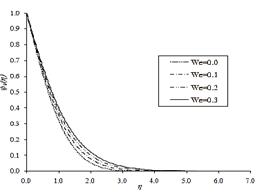
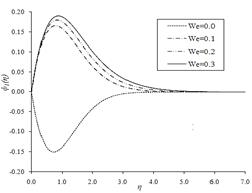
Ariel [24]. Figure 1 shows the profiles of
are shown in Table 1. These values
are in good agreement with the values obtained by Garg and Rajagopal [23] and
Ariel [24]. Figure 1 shows the profiles of ![]() for various values of
for various values of ![]() . We observed that as the elasticity
of the fluid increases, the velocity near the wall decreases.
. We observed that as the elasticity
of the fluid increases, the velocity near the wall decreases.
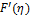 for various values of
for various values of 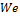 .
. Letting ![]() , then system (19) gives
, then system (19) gives
and
Letting ![]() , then system (21 a-b) gives
, then system (21 a-b) gives
System
(23 a-b) is solved numerically using a shooting method and it is found that for ![]() ,
, ![]() Since
Since ![]() , then for
, then for ![]() ,
, ![]() which is in good agreement with the value
obtained by Takemitsu and Matunobu [16]. Numerical values of
which is in good agreement with the value
obtained by Takemitsu and Matunobu [16]. Numerical values of ![]() for different values of
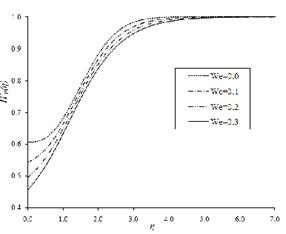
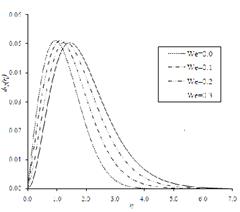
for different values of ![]() are shown in Table 1. Figure 2 depicts the
profiles of
are shown in Table 1. Figure 2 depicts the
profiles of ![]() for various values of
for various values of ![]()
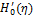 for various values of
for various values of 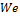 .
.Table 1.
Numerical values of ![]()
![]() and
and ![]() for different values of
for different values of ![]() .
.
| 0.0 | 23259 | 0.60777 | -0.81107 | -0.49348 | 0.09471 |
| 0.1 | 1.13425 | 0.54392 | -0.76774 | 0.50612 | 0.06023 |
| 0.2 | 1.05818 | 0.49546 | -0.73291 | 0.51309 | 0.02785 |
| 0.3 | 0.99689 | 0.45677 | -0.70364 | 0.51685 | -0.00204 |
| 0.4 | 0.94588 | 0.42465 | -0.67826 | 0.51881 | -0.02953 |
| 0.5 | 0.90248 | 0.39774 | -0.65619 | 0.51922 | -0.05474 |
| 1.0 | 0.75276 | 0.30691 | -0.57522 | 0.51155 | -0.15428 |
| 2.0 | 0.59677 | 0.21662 | -0.48170 | 0.48461 | -0.27270 |
| 5.0 | 0.41288 | 0.12046 | -0.35721 | 0.41638 | -0.39192 |
| 8.0 | 0.33533 | 0.08503 | -0.29916 | 0.37114 | -0.40062 |
| 10 | 0.30283 | 0.07127 | -0.27371 | 0.34885 | -0.38807 |
| 20 | 0.21857 | 0.03978 | -0.20475 | 0.28684 | -0.37758 |
| 50 | 0.14008 | 0.01735 | -0.13476 | 0.19505 | 0.16073 |
| 100 | 0.09951 | 0.00897 | -0.09591 | 0.14291 | 0.33255 |
| 200 | 0.07053 | 0.00453 | -0.06490 | 0.08305 | 1.48595 |
| 500 | 0.04469 | 0.00180 | -0.02550 | -0.04243 | 3.12615 |
Letting ![]() , then system (22 a-b) becomes
, then system (22 a-b) becomes
The only parameter in equation (24a) is the frequency ![]() . Two series
solutions valid for small and large
. Two series
solutions valid for small and large ![]() respectively
will be obtained. For small values of the frequency
respectively
will be obtained. For small values of the frequency![]() , we assume that
, we assume that
where the numerical values for ![]() and
and ![]() are given in Table 1 for different values of
are given in Table 1 for different values of ![]() .
.
For large values of the frequency ![]() , we let
, we let
![]() and
and
and it was found that
where ![]() and the numerical values of
and the numerical values of ![]() are given in Table 1 for different values of
are given in Table 1 for different values of ![]() . Figures 3-5 depict the variations of
. Figures 3-5 depict the variations of ![]() ,
, ![]() and
and ![]() for various values of
for various values of ![]() .
.
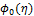 for various values of
for various values of 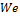 .
.
 for various values of
for various values of  .
.
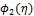 for various values of
for various values of 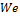 .
.4. Solutions in the Moving Frame of Reference
We assume that the Cartesian coordinates ![]() are moving with the plate, the
are moving with the plate, the ![]() -axis is
along the plate and the
-axis is
along the plate and the ![]() -axis is
normal to the plate. In this case, following Takemitsu and Matunobu [16], we
assume that the streamfunction is given by
-axis is
normal to the plate. In this case, following Takemitsu and Matunobu [16], we
assume that the streamfunction is given by
and the boundary conditions are given by
We note that the flow is
oscillating with velocity ![]() at infinity. Using equation (28) in (9),
equating different powers of
at infinity. Using equation (28) in (9),
equating different powers of ![]() to zero and
integrating once with respect to
to zero and
integrating once with respect to ![]() using the
conditions at infinity, we obtain
using the
conditions at infinity, we obtain
and
Non-dimensionalizing using
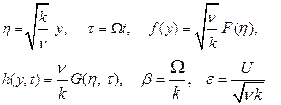
we obtain
and
System
(33 a-b) has been solved numerically in section 3. Letting ![]() , system (34 a-b) gives
, system (34 a-b) gives
and
Numerical solutions of system (35 a-b) have been obtained in section 3. It can easily be shown that the function
is a solution
of system (36 a-b) since it satisfies both the equation and the boundary
conditions. In equation (37), the functions ![]() and
and ![]() have been found in section 3.
have been found in section 3.
4. Discussion and Conclusions
The unsteady second grade
stagnation-point flow impinging obliquely on an oscillatory flat plate is
studied. Numerical results for this flow are found for various values of the
Weissenberg number ![]() . Figure 1 shows the variations of
. Figure 1 shows the variations of ![]() for various values of
for various values of ![]() . The effect of the Weissenberg number,
. The effect of the Weissenberg number, ![]() , is to decrease the velocity
, is to decrease the velocity ![]() near the wall as it increases. Figure 2 depicts
the variations of
near the wall as it increases. Figure 2 depicts
the variations of ![]() for various values of
for various values of ![]() and shows that
and shows that ![]() decreases near the wall as
decreases near the wall as ![]() is increasing. The variations
of
is increasing. The variations
of ![]() with various values of
with various values of ![]() are shown in Figure 3. From this
figure we observed that
are shown in Figure 3. From this
figure we observed that ![]() is decreasing as
is decreasing as ![]() is incresing. Figure 4 shows the
variations of
is incresing. Figure 4 shows the
variations of ![]() for various values of
for various values of ![]() and Figure 5 depicts the variations
of
and Figure 5 depicts the variations
of ![]() for various values of
for various values of ![]() . From Table 1,
. From Table 1, ![]() is decreasing as
is decreasing as ![]() is increasing.
is increasing.
References
[1] K. Hiemenz, "Die Grenzschicht an einem in den gleichformigen Flussigkeitsstrom eingetauchten geraden Kreiszylinder," Dingler's Polytech., vol. 326, pp. 321, 1911. View Article
[2] J. T. Stuart, "The viscous flow near a stagnation point when the external flow has uniform vorticity," J. Aerospace Sci., vol. 26, pp. 124, 1959. View Article
[3] K. J. Tamada, "Two-dimensional stagnation point flow impinging obliquely on a plane wall," J. Phys. Soc. Japan, vol. 46, pp. 310, 1979. View Article
[4] J. M. Dorrepaal, "An Exact solution of the Navier-Stokes equation which describes non-orthogonal stagnation-point flow in two dimensions," J. Fluid Mech., vol. 163, pp. 141, 1986. View Article
[5] B. W. Beard and K. Walters, "Elastico-viscous boundary layer flows," in Proceedings of Camb. Phil. Soc., 1964.
[6] J. M. Dorrepaal, O. P. Chandna and F. Labropulu, "The flow of a visco-elastic fluid near a point of re-attachment," ZAMP, vol. 43, pp. 708, 1992. View Article
[7] F. Labropulu, J. M. Dorrepaal and O. P. Chandna, "Viscoelastic fluid flow impinging on a wall with suction or blowing," Mech. Res. Comm., vol. 20, no. 2, pp. 143, 1993. View Article
[8] N. Rott, "Unsteady viscous flow in the vicinity of a stagnation point," Quart. of Appl. Math, vol. 13, pp. 444, 1956. View Article
[9] M. B. Glauert, "The laminar boundary layer on oscillating plates and cylinders," J. Fluid Mech., vol. 1, pp. 97, 1956. View Article
[10] A. C. Srivastava, "Unsteady flow of a second-order fluid near a stagnation point," J. Fluid Mech., vol. 24, no. Part 1, pp. 33, 1966. View Article
[11] C. H. Yih, Fluid Mechanics, New York: West River Press, 1977.
[12] F. Labropulu, X. Xu and M. Chinichian, "Unsteady Stagnation Point Flow of a non-Newtonian Second-Grade Fluid," Int. J. Math. & Math. Sci., vol. 2003, no. 50, pp. 3797-3807, 2003. View Article
[13] Y. Matunobu, "Structure of pulsatile Hiemenz flow and temporal variation of wall shear stress near the stagnation point. I," J. Phys. Soc. Japan, vol. 42, pp. 2041, 1977. View Article
[14] Y. Matunobu, "Structure of pulsatile Hiemenz flow and temporal variation of wall shear stress near the stagnation point. II," J. Phys. Soc. Japan, vol. 43, pp. 326, 1977. View Article
[15] M. Kawaguti and K. Hamano, "Two-dimensional model of pulsatile flow through constricted artery," in Xth Intern. Congr. Angiology, 1976.
[16] N. Takemitsu and Y. Matunobu, "Unsteady stagnation-point flow impinging oqliquely on an oscillating flat plate," J. Phys. Soc. Japan, vol. 47, no. 4, pp. 1347, 1979. View Article
[17] Y. Matunobu and M. Arakawa, "Model experiment on the post-stenotic dilatation in blood vessels," Biorhelogy, vol. 11, pp. 427, 1974. View Article
[18] B. Gessner, "Hemodynamic theories of atherogenesis," Circulation Research, vol. 33, pp. 259, 1973. View Article
[19] R. S. Rivlin and J. L. Ericksen, "Stress-deformation relations for isotropic materials," J. Rat. Mech. Anal., vol. 4, pp. 323, 1955. View Article
[20] J. E. Dunn and R. L. Fosdick, "Thermodynamics, stability and boundedness of fluids of complexity 2 and fluids of second grade," Arch. Rational Mech. Anal., vol. 56, pp. 191, 1974. View Article
[21] J. E. Dunn and K. R. Rajagopal, "Fluids of differential type:critical review and thermodynamic analysis," Int. J. Eng. Sci., vol. 33, pp. 689, 1995. View Article
[22] C. Truesdell, "The Mechanical foundations of elasticity and fluid dynamics," Journal of Rational Mechanics and Analysis, vol. 1, pp. 125, 1952. View Article
[23] V. K. Garg and K. R. Rajagopal, "Stagnation point flow of a non-Newtonain fluid," Mech. Res. Comm., vol. 17, no. 6, pp. 415, 1990.
[24] P. D. Ariel, "A hybrid method for computing the flow of viscoelastic fluids," Int. J. Num. Meth. in Fluids, vol. 14, pp. 323, 1992. View Article
[25] P. D. Ariel, "On extra boundary condition in the stagnation point flow of a second grade fluid," Int. J. Engng. Sci, vol. 40, pp. 145, 2002. View Article
[26] R. E. Bellman and R. E. Kalaba, in Quasilinearization and Non-Linear Boundary Value Problems, New York, Elsevier, 1965. View Article

