Journal of Fluid Flow, Heat and Mass Transfer (JFFHMT)

ISSN: 2368-6111

Weather Prediction and the Ideal Gas Law

Genesis Limon¹, Dr. Surupa Shaw¹

¹Texas A&M University, Department of Multidisciplinary Engineering
glimon_2023@tamu.edu; surupashaw@tamu.edu

Abstract - The Ideal Gas Law (PV = nRT) serves as a cornerstone for understanding relationships among pressure, temperature, and volume in atmospheric systems. This paper aims to provide an interdisciplinary review of the Ideal Gas Law’s role in modeling meteorological and planetary atmospheres, with the central research question focusing on how thermodynamic principles particularly the Ideal Gas Law can enhance the accuracy of meteorological models. The study integrates insights from physics, environmental engineering, and climate science, combining a literature-based evaluation with computational analyses using atmospheric datasets. Results indicate that while the Ideal Gas Law effectively models vertical air motion and pressure variations under standard conditions, it demonstrates notable limitations during extreme weather phenomena. The findings highlight the need for developing hybrid models that incorporate real gas behavior and artificial intelligence to improve forecasting precision and broaden applicability across diverse atmospheric environments.

Keywords: Ideal gas law, Modeling meteorological Computational, analyses, Hybrid models.

© Copyright 2025 Authors - This is an Open Access article published under the Creative Commons Attribution License terms Creative Commons Attribution License terms. Unrestricted use, distribution, and reproduction in any medium are permitted, provided the original work is properly cited.

Date Received: 2025-04-23
Date Revised: 2025-10-29
Date Accepted: 2025-12-01
Date Published: 2025-12-16

1. Introduction

The Ideal Gas Law, expressed as P·V = n·R·T, describes the relationship between pressure (P), volume (V), temperature (T), and the number of moles (n) of a gas (Kautz et al. [1]). Kautz found students struggled to connect concepts like heat, internal energy, and temperature in real-world systems. Experiments showed that rising air, driven by low pressure, leads to precipitation. This law helps explain how gases behave in the atmosphere. Because pressure, temperature, and volume constantly change, it’s essential for forecasting. Tenny et al. [2] note that gases behave ideally under low pressure (below 1 atm) and high temperature (above 300 K) common in the upper atmosphere. Teddy expands this by applying the law to gas mixtures, modifying it to Pi·V = ni·R·T, where Pi is the partial pressure of gas i. This adaptation suits atmospheric gases like nitrogen, oxygen, and carbon dioxide, aiding in accurate weather and climate models.

Meteorology, as defined by Gupta et al. [3], studies atmospheric phenomena like temperature, pressure, humidity, and wind—all governed by gas laws. The book emphasizes how seasonal and weather changes impact industries, and understanding these variables improves climate predictions. The Ideal Gas Law explains how temperature and pressure shifts drive air movement, cloud formation, storms, and winds. Fathi et al. [4] explain atmospheric motion is driven by temperature gradients and pressure differences, making the law essential in weather modeling. Forecasting remains challenging due to changing parameters like seasons, geography, and data accuracy. Technology and data mining have improved precision by better analyzing temperature and pressure fluctuations. Given the Ideal Gas Law’s relevance in other areas, this paper will cover a wide range to help understand its application in Earth’s atmosphere, other planetary atmospheres, and computational modeling, such as AI and Machine Learning.

A major meteorological use of the Ideal Gas Law is in understanding air pressure systems. Warm air expands and becomes less dense, forming low-pressure systems and storms. Cool air contracts and becomes denser, creating high-pressure systems and clear skies. These relationships help forecast weather. The law also explains air pollution behavior. Choudhary et al. [5] studied how pollutants like ozone and particulates interact with atmospheric conditions, affecting climate and air quality. They cited the Great Smog of London (1952), where chemical reactions created ground-level ozone, causing over 8,000 deaths. Jacob et al. [6] show that ozone levels correlate with temperature and pressure. U.S. data from 1980–1998 show that a 3K rise can double the chance of ozone levels exceeding 80 ppb, linking gas behavior to pollution and climate.

Kinney et al. [7] explain that rising temperatures speed up pollutant-forming reactions, while circulation spreads pollutants, affecting weather. The California Climate Change Center developed an ozone prediction model using ambient temperature, showing NOx emissions can double as temperature rises from 45°F to 95°F. Precipitation and wind also influence airborne dust, dispersing pollutants. This link between thermodynamics and environmental meteorology shows the Ideal Gas Law's importance in quantifying gas behavior and pollution spread.

Beyond forecasting, the Ideal Gas Law is key to climate change studies. Manisalidis et al. [8] explain that greenhouse gases trap heat, disrupting pressure balance and intensifying weather like hurricanes, droughts, and heat waves. While the greenhouse effect helps stabilize temperatures, excessive emissions lead to global warming, raising atmospheric temperature and pressure. Sharma et al. [9] discuss how warming alters pressure systems, precipitation, and wind, linking gas behavior to climate variability. Houghton et al. [10] note that energy transfer drives air expansion and contraction, influencing storms and temperature shifts. Of incoming solar radiation, 30% is reflected, 50% absorbed by the surface, and 20% by the atmosphere. Imbalances drive circulation patterns like cyclones and weather fronts, requiring accurate models.

Flasar et al. [11] compare Earth's atmosphere to others, emphasizing the need to understand gas behavior in meteorology. Atmospheric motion models using the Ideal Gas Law predict large-scale events like hurricanes and monsoons. The World Meteorological Organization seeks to improve observations and climate solutions (Merlon et al. [12]). Researchers aim to refine measurements and technology for better predictions. A challenge is temperature data uncertainty due to scale shifts. Even minor shifts (0.01°C to 0.04°C) affect data collection. Understanding how temperature, pressure, and environment influence atmospheric motion is key to predicting extreme weather.

Holton et al. [13] explore how pressure and temperature changes drive cyclones, jet streams, and fronts—core meteorological features. They explain the pressure-height relationship, where vertical stretching compresses air, creating cyclonic storms. Advanced models are needed to predict such events, but remain limited by approximations, though tech advances have improved accuracy.

Meteorological tool development is rooted in gas laws. Fleming et al. [14] describe the evolution from barometers and thermometers to satellites and computational models. Modern meteorology depends on tools developed during the Cold War, Space Age, and Atomic Age. Makino et al. [15] explain that weather models use the Ideal Gas Law to simulate atmospheric change, employing equations like Euler’s and the barotropic equation of state, which link pressure, density, and temperature.

Kowalski et al. [16] discuss data assimilation advancements that improve model accuracy using gas laws. They refined the definition of averaging by applying air weighting parameters, improving atmospheric representation and weather prediction.

In summary, the Ideal Gas Law is central to meteorology, explaining gas behavior under changing conditions. It governs the relationships between temperature, pressure, and volume, aiding in weather prediction, pollution analysis, and climate modeling. Its principles enable the creation of advanced meteorological tools, helping scientists better understand Earth’s dynamic weather systems.

Fundamentals of the Ideal Gas Law in Atmospheric Science

2. 1. Definition and mathematical formulation

Jacobson et al. [17] state that the Ideal Gas Law combines Boyle’s, Charles’s, and Avogadro’s Laws. Boyle’s Law describes the inverse relationship between pressure and volume when temperature is constant low pressure at high altitudes can cause explosions due to expanding gas. Charles’s Law shows that volume and temperature are directly proportional when pressure is constant. Avogadro’s Law explains that equal volumes of gases at the same temperature and pressure contain the same number of moles, establishing a direct link between volume and mole count. And Jacobson concludes that combining these three laws results in the Ideal Gas Law formula: P·V = n·R·T.

Table 1. Laws and their respective relationships.

Law	Relationship
Boyle’s Law	P ∝ 1/V
Charle’s Law	V ∝ T
Avogadro’s Law	V ∝ n
Ideal Gas Law	PV ∝ T , [P*V=n*R*T]

2. 2. Assumptions and Limitations in Meteorological Applications

Ambaum et al. [18] outline key assumptions when working with ideal gas mixtures. One assumption is that gases at the same temperature can be treated as a single mixture, neglecting each other’s presence. Inelastic collisions with container walls are also ignored, as they are not believed to affect results. The model further assumes non-interacting molecules, with intermolecular distances not considered. Additionally, it is assumed that the system remains in thermal equilibrium, although this requires molecular collisions, which introduces limitations. Real-world factors such as humidity in air and salinity in water influence system behavior and may require alternative gas law derivations

2. 3. Assumptions and Limitations in Meteorological Applications

Woody et al.[19] explains that ideal gases are those that have measurable properties such as pressure, volume, and temperature, and gases in the limit of zero pressure, meaning they do not exist. This leads the ideal gas law to approximate gases to a certain description. However, Woody also explains that we assume for the law to represent real gases, which it fails to do because the true requirements aren’t fully met. According to Sokovnin et al.[20] real gases molecular interactions, as well as diverse conditions different from the ideal gas, for example, high pressures and low temperatures. The article states that as a result, using the ideal gas law as a model leads to significant errors in calculations, particularly under conditions that exceed 10 atm or temperature drops below 200 K. These effective real gases are then significantly used in engineering applications to better approach the different models taken.

3. Atmospheric pressure systems and weather patterns

3. 1. A Role of the Ideal Gas Law in High- and Low-Pressure Systems

Craige et al. [21] explain that Earth’s layers affect atmospheric behavior, with solar radiation causing temperature shifts in different regions. In high-radiation areas, absorbed heat raises temperatures beyond normal levels. Huang et al. [22] note that atmospheric components like oxygen, nitrogen, and carbon dioxide affect water vapor content, which varies with pressure and temperature. Their study refined the Clausius-Clapeyron equation to calculate saturation vapor pressure (SVP) more precisely, incorporating terms from the Ideal Gas Law, such as specific volume. The new equations produced relative errors as low as 0.001%–0.006%, significantly improving accuracy over the old model. The table provides the results generated in the study.

Table 2. Saturation Vapor Pressure and Relative Error for Water calculated from different equations.

	Water (T > 273.15 K)
	Temperature (K)	Pressure (Pa)	SVP (Ps)	RE (%)
Old Equation	313.15	7384.94	7374.72	0.14
New Equation	313.15	7384.94	7384.93	0.0001

Table 3. Saturation Vapor Pressure and Relative Error for Ice calculated from different equations.

	ICE (T ≤ 273.15 K)
	Temperature (K)	Pressure (Pa)	SVP (Ps)	RE (%)
Old Equation	233.15	12.8412	12.834	0.055
New Equation	233.15	12.8412	12.841	0.004

Tables 2 and 3 compare saturation vapor pressure (SVP) values for water and ice using traditional and refined equations. The refined model, which incorporates Ideal Gas Law parameters like specific volume, significantly reduces relative error down to 0.0001% for water and 0.004% for ice. This precision is vital in meteorology, where SVP governs cloud formation, humidity profiles, and precipitation onset. Accurate SVP calculations improve the reliability of weather models, especially in predicting fog, dew point, and convective activity across varying temperature regions.

3. 2. Temperature Variations and Their Impact on Air Movement

Landberg et al. [23] explain that air movement isn’t solely driven by pressure or temperature, but by energy distribution, regions near the equator receive more solar energy, causing warm air to rise, while cooler polar air sinks. This circulation, influenced by Earth’s rotation and atmospheric layers, creates the wind patterns. Hartmann et al. [24] add that clouds impact surface temperature by affecting condensation and radiation transfer. Strong, high clouds form in cold conditions; clear skies are common in warmer ones. Their comparison of Antarctica and California supports Landberg’s point: Death Valley, north of the equator, is among the warmest places, while Vostok in Antarctica, near the South Pole, is among the coldest.

Table 4. Temperature difference in locations.

Location	Temperature(K)	Details
Surface of the Earth	288.15
Vostok, Antarctica	183.95	Coldest Temperature Closest to the Poles
Furnace Creek Ranch Death Valley, California	329.85	Warmest Temperature Closest to the Equator

Table 4 illustrates temperature extremes between Vostok, Antarctica and Death Valley, California. These values highlight the role of solar radiation and latitude in driving atmospheric convection. The Ideal Gas Law helps explain how warmer temperatures in equatorial regions cause air expansion and uplift, while colder polar temperatures lead to contraction and subsidence. This dynamic underpins global circulation patterns and wind systems, reinforcing the law’s utility in modeling vertical air movement and regional climate behavior.

3. 3. Formation of Weather Fronts and Cyclonic Systems

Brâncuş et al. [25] examine cyclone structure and the forces behind strong winds. They identify three key features: the warm sector, which accelerates air toward the cyclone center; the cold conveyor belt, an airstream wrapping around the center; and the sting jet, which descends from the middle of the cloud head. The study analyzes two merging cyclones and documents the first sting jet in a Mediterranean system. Data showed that wind maxima form under specific pressures and temperature variations, indicating atmospheric stability and intensity. The sting jet notably affects cloud formation and increases wind acceleration, enhancing cyclone strength.

Table 5. Wind Maxima and their respective parameters.

Wind Maxima	Wind Speeds (m/s)	Pressure (hPa)	Temperature (K)	Structure
W1	45 m/s	925 hPa	288 – 292 K	Tear-shaped footprint near the center. Related to sting jet features
W2	40 – 45 m/s	925 hPa	286 – 288 K	Smaller footprint than W1. Positioned west of W1
W3	40 – 45 m/s	925 hPa	287 – 289 K	Elongated structure with ascending air at edge and descending air at rear.

Table 5 presents wind maxima associated with sting jets in Mediterranean cyclones. The data show how specific pressure and temperature ranges, like 925 hPa and 288-292 K, correlate with intense wind structures. These findings demonstrate how the Ideal Gas Law helps quantify air density and pressure gradients that drive cyclonic acceleration. Understanding these relationships is crucial for predicting storm intensity and structure, especially in mid latitude systems.

4. Temperature, Density, and Vertical Air Movement

4. 1. Buoyancy and Atmospheric Convection

Grabowski et al. [26] define buoyancy as

(1)

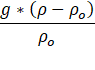
where ρ represents air density. Buoyancy depends on factors like temperature, pressure, and water vapor. Two major influences are phase changes in water and precipitation. Phase changes alter air temperature and mixing ratios higher temperatures increasing buoyancy. As Precipitation leaves the volume, it can also raise buoyancy.

Table 6. Impact on buoyancy based on atmospheric parameters.

Simulations	Impact on buoyancy	Data Examples
Temperature	Increases buoyancy	Increasing temperature by 2.5 K increases buoyancy by 0.01 g/kg
Precipitation (offloading of q)	Increases buoyancy with mass decrease	1 g/kg of offloading of q leads to an increase in buoyancy by 0.001 g
Water Vapor Content ( )	Increases buoyancy through latent heat release	at 10 g/kg increases buoyancy greatly
Condensate Loading (q)	Reduces buoyancy through mass increase	q = 1 g/kg reduces buoyancy by 0.001 g

Table 6 quantifies how temperature, precipitation, water vapor, and condensate presence affect atmospheric buoyancy. For instance, a 2.5 K temperature increase increases buoyancy by 0.01 g/kg. These relationships are governed by the Ideal Gas Law, which links temperature and density to vertical motion. Enhanced buoyancy drives convection and cloud development, making these metrics important for modeling storm formation and boundary layer dynamics.

Anisimov et al. [27] describe how surface heating initiates atmospheric convection, forming an unstable planetary boundary layer (PBL). This creates an entrainment zone and a convective boundary layer (CBL), whose height determines turbulence intensity. Using temperature profiles, they linked surface heating to increased buoyancy and CBL growth—reinforcing Grabowski’s findings.

4. 2. The Lapse Rate and Tropospheric Temperature Gradients

Stone et al. [28] found that height, latitude, and season significantly influence vertical temperature, with lapse rates being nearly moist adiabatic at 300K and sub-adiabatic near 250K. Lapse rates are more stable at higher latitudes, depending on the season, with 20% of the moist adiabatic lapse rate observed at the equator, peaking at 30N in January and 50N in July. Two atmospheric regimes based on these lapse rates are described in the table below.

Table 7. Latitude Regime and their respective lapse rates

Low Latitude regime	Lapse rates are more adiabatic.
High Latitude regime	Lapse rates are the critical lapse rate for bioclinic adjustments.

Table 7 distinguishes lapse rate behavior across latitudes. Low latitude regions exhibit more adiabatic lapse rates, while high latitude zones approach critical level for bioclinic adjustments. These gradients influence vertical temperature profiles and atmospheric stability. The Ideal Gas Law supports these interpretations by relating temperature and pressure to air density, helping forecast phenomena like jet streams and frontal boundaries.

Stone also mentions that “eddies” are driven by horizontal temperature gradients and topography, not the surface. Xu et al. [29] discusses how tropospheric delays impact GPS precision. They used two methods: one to correct delays with a model and another to estimate delays as unknowns. Temperature and pressure effects were considered in the models, showing how GPS performance varies with latitude. Results are shown in the table below, demonstrating the importance of accurate data for capturing temperature and topography variations.

Table 8. Different models and their results on precision.

Models	Improvement of Direction	Limitations
Model 1	(Up) by 25% under a 5-degree elevation cut off angle	Less accurate in high-latitude conditions (e.g. in Antarctica)
Model 2	(North) by 51%, (East) by 15%, (Up) by 30%. In low latitude and high humidity conditions.	Requires precise angle data

Table 8 compares two GPS delay correction models under varying meteorological conditions. Model 2 shows up to 51% improvement in the northern direction under humid, low latitude conditions. These results underscore the importance of including temperature and pressure data governed by the Ideal Gas Law into GPS based atmospheric measurements. Accurate modeling of tropospheric delays enhances satellite based forecasting and geolocation precision.

4. 3. Cloud Formation and Precipitation Mechanisms

Li et al. [30] explain how aerosols impact radiation, energy absorption, and cloud formation. Absorbing aerosols cause thermodynamic changes due to adiabatic heating and reduce cloud fractions. Aerosol-Cloud Interactions (ACIs) influence cloud size, thickness, and precipitation by altering droplet size and number. Factors like temperature and humidity affect these interactions, leading to mixed-phase clouds and variations in radiative forcing and precipitation characteristics.

5. The Ideal Gas Law and Air Pollution Dynamics

5. 1. Gas Law Applications in Air Quality Modeling

According to Sokhi et.al [31] air pollution has been an essential tool for research and scientific investigation of the atmospheric process. It has led to the development of computational methods, techniques, and numerical weather predictions. The multiscale mesoscale now allows comprehension of air pollution and the ability to analyze and explain the changes in pollutant concentrations, which serve to process weather prediction. Pleim et.al [32] state that “surface fluxes” have multiple chemicals that are involved in the air quality modelling and have multiple pathways in exchange with the surface and ground amongst other things. To be able to apply the gas law into chemical calculations can have a better effect on modelling algorithms and the types of air qualities that arise from the use of chemicals.

Table 9. Equation Models and their connection to the gas law.

Equations Models	Purpose for Air Quality Modeling	Connection with the Gas Law
Manin-Obukhov similarity theory	This equation models the turbulent fluxes of heat, moisture, momentum, and chemical species of atmospheric quantities	Tied to the vertical profile of temperature and pressure
Dry Deposition Model	Heat, moisture, momentum, and trace chemical species	Implement pressure and molecular diffusivity
Aerodynamic Resistance	Represents resistance to flux by turbulent diffusion in the surface layer	Dependent on temperature and pressure gradients

Table 9 outlines equations used in air quality modeling, such as the Manin-Obukhov similarity theory and aerodynamic resistance. These models rely on temperature and pressure gradients, directly tied to the Ideal Gas Law. By estimating how gases behave under varying conditions, these equations improve pollutant dispersion simulations and enhance environmental forecasting accuracy.

5. 2. The Effect of Temperature and Air Pressure on Pollutant Dispersion

Giovannini et al. [33] explain that temperature stratification controls turbulent mixing and traps pollutants, especially in mountainous areas where limited solar radiation and nocturnal winds cause cold air to settle. Zhang et al. [34] highlight the influence of meteorological variables, temperature, pressure, and humidity on air quality dynamics. Using models like the Granger causality test, they found air pollution is mainly driven by self-aggregation and self-diffusion rather than external dispersion.

Table 10. Impact on pollution based on various meteorological factors.

Meteorological Factors	Self-cumulative impact	Influence on Pollution
Extreme Wind Speeds	7.53% across 5 periods	Causes turbulence and therefore an increase in pollution dispersion
Sunshine Duration	2.14% across 4 periods	Longer duration increases temperature and therefore breaks the trap pollutants
Average Humidity	Interacts with extreme wind speeds and sunshine duration	Higher humidity reduces pollution dispersion
Average Wind Speed	Interacts No impact on air quality	No impact on pollution dispersion
Rainfall Capacity	No observed relationship with air quality	No impact on air pollution (Insignificant amount)

Table 10 evaluates how extreme wind speed (above 39 mph), sunshine duration and average humidity all have an impact on the diffusion of pollutants by having a direct relationship with air quality. For example, extreme wind speeds increase dispersion by 7.53%, while higher humidity restrains it. These effects are connected by thermodynamic principles, with the Ideal Gas Law providing a framework to model how temperature and pressure changes alter air density and mixing efficiency. This is critical for predicting pollution hotspots and designing mitigation strategies.

5. 3. Impact of Greenhouse Gases on Climate Change

Paciorek et al. [35] link greenhouse gas emissions, primarily from deforestation and fossil fuel burning, to global warming and increased interest in climate policy. Greenhouse gases trap heat, constantly changing Earth’s climate. A case study on Texas’s 2011 summer used global climate models to compare current and counter (past)scenarios. These results showed how human-induced emissions were the cause for these increased climate events, proving their impact on extreme weather and climate change such as hot summers, droughts, and the increase of heatwaves.

6. Applications in Weather Forecasting and Climate Modeling

6. 1. Numerical Weather Prediction (NWP) Models and Gas Law Integration

Deconinck et al. [36] highlight that advance in computer processing, such as faster CPUs, more cores, and enhanced memory allow for more complex and accurate weather models. These improvements allow for higher resolution simulations and more accurate representations of atmospheric processes. Weyant et al. [37] stress the importance of advanced models to assess human-driven climate change. These models use gas laws to simulate greenhouse emissions and their effects, improving regional climate predictions. These computational models also facilitate forecasting, uncertainties, and real-time data understanding, further improving reliability.

6. 2. Remote Sensing and Satellite-Based Atmospheric Measurements

According to Bourassa et.al [38] Remote sensing has allowed them to look deeper into the surface winds (scalar and vector), surface stress, air-sea heat fluxes, currents, sea state, and precipitation. These different models, technologies, and networks have allowed them to retrieve ocean speed winds and direction, improve data and information systems, and create visualized grids through the implementation of satellites.

Table 11. Technology/sensors and their performance.

Technologies/Networks	Purpose
Scalar Speeds Sensors	Measures wind speed over the ocean by analyzing power spectrum of electromagnetic radiation emitted by water surface
Vector Wind Sensors	Wider range of applications than scalar winds
Scatterometers	Active microwave radars, evaluate coverage, and directional performance
Polarimetric Radiometer	Include left-to-right circular polarized channels and vertical/horizontal polarization. Full information on polarization
Synthetic Aperture Radae (SAR)	Retrieve wind speed and direction information
Costal High Frequency Radar	Operates frequency ranges

Table 11 outlines remote sensing technologies used to measure atmospheric variables such as wind speed, surface stress, and precipitation. These sensors like scatterometers and polarimetric radiometers, rely on electromagnetic interactions that are influenced by temperature and pressure gradients. The Ideal Gas Law helps interpret these gradients by linking them to air density and motion. Accurate sensor data, when integrated with gas law principles, enhances the resolution of weather models, and supports real time forecasting.

Aguiar et.al [39] state the importance of a reliable forecasting model, global horizontal irradiance (GHI) can provide them with the tools needed to avoid unstable behaviors in the electrical grid. Among the many different methods this forecasting uses it would be satellite image models. The geostationary satellite method allows them to gather images all around the world in less than an hour, and various other methods can quickly produce data that would serve to estimate the weather.

6. 3. Long-Term Climate Trends and Global Temperatures Variations

Giorgi et al. [40] highlight Regional Climate Models (RCMs) as tools to downscale Global Climate Models (GCMs) for more localized forecasts. He notes warming at high elevations in the Alps due to heavy precipitation, a trend challenging to capture with RCMs due to terrain complexity. Bathiany et al. [41] analyzed monthly temperature variability and found the largest changes in mid-to-high latitudes during Boreal autumn and winter. In high latitudes, decreased variability is linked to sea-ice loss and high heat capacity. However, horizontal winds and weakened meridional temperature gradients also reduce variability, especially in mid-latitudes.

7. Extreme Weather Events and their relationship to Atmospheric Gases

7. 1. Heatwaves and Atmospheric Stability

Barriopedro et al. [42] define heat waves as extended periods of high temperatures driven by stable atmospheric conditions that trap heat and reduce convection. Global warming is expected to increase their frequency. Positive and negative buoyancy in warm and cold regions intensify this effect. Rostami et al. [43] explain that trapped heat can disrupt stability, creating buoyancy anomalies and generating inertia-gravity waves that impact heat, momentum distribution, and weather systems.

Table 12. Connection of buoyancy and Inertia-Gravity waves with levels of the atmosphere.

	Midlatitude	Lower Troposphere	Upper Troposphere
Positive buoyancy waves	Disturb atmospheric stability	Initiate cyclonic circulation patterns	Cause anticyclonic circulation patterns
Inertia-Gravity waves	Disturbance with high large amplitude causes inertia-gravity waves to disperse equatorward to the tropical region	Such cyclonic patterns interact with the atmosphere, leading to the development of inertia gravity waves	The involvement of inertia gravity waves leads to atmospheric adjustments

Table 12 connects buoyancy anomalies and inertia-gravity waves to atmospheric stability across different layers. Positive buoyancy in the lower troposphere initiates cyclonic circulation, while upper-level disturbances lead to anticyclonic patterns. These dynamics are governed by pressure and temperature gradients, which the Ideal Gas Law helps quantify. Understanding these wave interactions is essential for modeling heatwaves, jet streams, and other extreme weather propagation.

7. 2. The Role of Gas Laws in Hurricane and Tornado Formation

According to Bělík et al. [43], vortex gas models have been developed to describe tornado maintenance by analyzing gas molecule behavior and temperature effects. In this context, negative temperatures are considered higher than positive ones, meaning energy increases lead to decreased entropy. Tornadic flows often exhibit negative temperatures greater than ambient vortices, which intensifies the tornado or expands its flow. Ben-Amots et al. [44] emphasize that a tornado’s source is the cloud above it. Using gas laws, they explain how decreasing pressure draws in air and vapor, releasing condensation that fuels the tornado. A warmer cloud base temperature supports tornado sustainability.

7. 3. Pressure Changes and Severe Thunderstorm Development

Allen et al. [45] states that thunderstorms will respond to warming and potentially a more variable climate change. Projections in recent models have shown an increase in warming and surface temperature and pressure perturbations, amongst other things. The more the rise nears the surface, there is an increase in the capacity to hold water and an increase in the amount of moisture in the air, eventually leading to a vertical thermodynamic instability. This causes a strengthening of energy and an increase of vertical velocity, leading to a favor in storms and a continuation of these severe storms as the instability increases.  The article talks about how seasons play a critical role in the development of such phenomena. This is because seasonal changes influence temperature variations and pressure patterns that are important in the development of such storms. The following table depicts how each phenomenon seems to be affected through specific seasons according to the article.

Table 13. Phenomena developed at different seasons.

Season	Phenomena	Pressure change impact
Spring/Summer	Tornadoes, Hailstorms, Thunderstorms	Temperature variations lead to major pressure changes, which lead to instability with winds
Summer	Hailstorms, Thunderstorms	Localized heat leads to low pressure and, therefore increases convection
Fall	Tornadoes, Thunderstorms	The transition from summer to fall causes temperature variations, which also generate pressure variations
Winter	Tornadoes, Thunderstorms	Warm winters lead to more low-pressure systems and create atmospheric instability

Table 13 outlines how tornadoes, hailstorms, and thunderstorms vary across seasons due to temperature-driven pressure changes. For example, spring and summer show increased instability from localized heating, which lowers pressure and increases convection. These seasonal shifts are directly tied to the Ideal Gas Law, which explains how rising temperatures expand air and reduce density, triggering vertical motion and storm formation. By quantifying these pressure temperature relationships, the law helps forecast seasonal storm risks and provide evacuation strategies.

8. Comparative Analysis: Earth's Atmosphere vs. Other Planetary Atmospheres

8. 1. Atmospheric Composition and Gas Behavior on Other Planets

Sánchez-Lavega et al. [46] highlight the importance of understanding exoplanet atmospheres especially their composition to infer planetary formation. The article compares solar system planets with Earth, focusing on atmospheric dynamics, aerosols, chemical composition, and temperature. The table below summarizes the study’s key findings.

Table 14. Atmospheric dynamics and chemical composition of different planets.

Planets	Atmospheric Pressure (at surface)	Temperature (°C)
Earth	1 atm (101.3 kPa)	~15 °C
Mercury	~10⁻¹⁴ atm	~167°C (average), up to 430°C day / -180°C night
Venus	92 atm	~465°C
Mars	0.006 atm	~–60°C
Jupiter	~1000 kPa ( at 1 bar level); increases with depth	~–145°C (upper atmosphere)
Saturn	~140 kPa (at 1 bar level)	~–178°C
Uranus	~120 kPa	~–197°C
Neptune	~100 kPa	~–201°C
Titan(moon of Saturn)	1.5 atm	~–179°C

Table 14 compares planetary atmospheres, showing how surface pressure and temperature vary dramatically from Venus’s 90 bar and 740 K to Uranus’s 0.1 bar and 49 K. These extremes challenge the assumptions of the Ideal Gas Law, which is most accurate under low pressure and high temperature. The table highlights how gas composition like, CO₂ on Venus, H₂/He on Jupiter, affects thermodynamic behavior, cloud formation, and energy transfer. This comparative analysis underscores the need for modified gas laws in planetary meteorology and helps understand Earth’s unique atmospheric stability. Gronoff et al. [47] emphasize the surface temperature’s role in stabilizing water and altering cloud formation, greenhouse gas effects, and atmospheric chemistry through absorbed and redistributed energy.

8. 2. Lessons from Extraterrestrial Atmospheres in Climate Science

Velichkova et al. [48] highlight extraterrestrial influences galactic-cosmic rays (GCR), solar activity, and orbital shifts on climate variables like temperature and ozone concentration, and humidity. GCR affects sea-level temperature with delayed responses and shows correlations with ozone and atmospheric moisture. King et al. [49] developed an improved evapotranspiration model using extraterrestrial radiation, offering gradual, more accurate climate projections than traditional models. The inclusion of extraterrestrial radiation enhances the predictive capacity of models used in agriculture, hydrology, and atmospheric gas components.

9. Future Research and Advancements in Meteorological Studies

9. 1. Improvements in Computational Fluid Dynamics for Weather Prediction

Bhatti et al. [50] begins by stating computational fluid dynamics (CFD) as a set of techniques made to assist a computer in providing a numerical simulation of the fluid flow. They state solutions that serve to visualize interactions between the layers of the fluids, examine a system’s performance, and design. He continues this by stating recent techniques such as PC clusters, showing large-scale simulations of different fluid flows on grids. These technologies, of course, are still open to improvements on how to fill the gaps of efficient solutions in the meteorological field. Blocken et al. [51] highlight the important role the CFD plays in societal challenges such as climate change, energy efficiency, health, etc. The article mainly focuses on how CFD is applied in urban physics. this includes the simulation of air pollution, microscale atmospheric modeling, and the Urban heat island effect. The following table provides an insight into how CDF is applied to such models and its connection to weather prediction.

Table 15. CFD contributions to different models.

Models	CDF contributions	Weather Prediction Connection
Air pollution	Simulates pollutant dispersion in urban areas. Helps predict the interaction between air quality and atmospheric conditions.	This contributes to the forecasting of smog and weather-related events.
Microscale atmospheric modeling	Simulates atmospheric boundary layer phenomena, which helps understand small processes like turbulence.	Directly enhance weather models by allowing the accuracy in the location of atmospheric behavior.
Urban Heat Island Effect	Illustrates how higher temperatures in urban cities are due to the heat retention of buildings.	Impacts weather patterns and refines prediction of heat waves and localized warming.

Table 15 details how Computational Fluid Dynamics (CFD) enhances weather prediction by simulating pollutant dispersion, microscale atmospheric behavior, and urban heat island effects. These models rely on pressure, temperature, and density inputs, core variables in the Ideal Gas Law. By integrating CFD with thermodynamic principles, meteorologists can better locate phenomena like smog formation and heat waves. The table illustrates how CFD bridges the gap between theoretical gas laws and real world atmospheric complexity.

9. 2. The Role of AI and Machine Learning in Atmospheric Science

Recent advances in machine learning (ML) have enabled the development of thermodynamically consistent models that adjust for deviations from ideal gas behavior in atmospheric and planetary simulations. Neural network–based equations of state (NNEoS) and free-energy learning approaches have demonstrated the ability to capture complex non-idealities by learning residual Gibbs or Helmholtz energy surfaces while preserving thermodynamic consistency through automatic differentiation, as expressed by Rosenberg et al. [52] and Kevrekidis et al. [53]. Similarly, graph neural networks (GE-GNNs) trained to predict excess Gibbs energy have been applied to model activity coefficients and gas–liquid equilibria in multicomponent atmospheric mixtures described by Kuang et al. [54]. In parallel, ML-based vapor pressure prediction models for low-volatility organic compounds have improved representations of gas–particle partitioning and secondary organic aerosol formation by accounting for non-ideal thermodynamic effects explained by Hyttinen et al. [55]. Collectively, these ML-driven thermodynamic models offer computationally efficient and physically consistent tools to represent real-gas and non-ideal behaviors essential for accurate atmospheric modeling.

9. 3. Potential Policy Implications for Climate and Weather Preparedness

Seto et al. [56] starts his article by stating that with the growing expansions of technology carbon emissions have been reducing more and more. Many factors influenced this, some being behavior influences and economic influences. These were often seen in developing countries in their regional pattern planning and transportation methods, followed by corporations and markets. All of this eventually led to the market industry based in an automobile economy. But with the large amount of gas usage they had, advertisements for government programs and projects for roads started to arise. When these concerns started becoming more and more noticeable, policies such as lower carbon intensity policies were implemented that allowed technologies to mature and build new dorms toward these developments.

10. Results

The simulations presented in this section are a combination of observational and modelled data. Real time meteorological datasets referenced include historical temperature and pressure data from the U.S National Centers for Environmental Information (NCEI) and satellite-derived wind and humidity data from scatterometers and radiometer platforms as described by Bourassa et al. [38]. Simulations and reanalysis data were gathered by global climate models (GCM’s) used in Paciorek et al. [35], and by tropospheric lapse rate and buoyancy models described in Grabowski et al. [26] and Stone et al. [28]. The referenced studies rely on comparable high resolution reanalysis and model outputs.

The Ideal Gas Law is a broad topic, and it’s application in meteorological contexts yielded valuable insights into atmospheric dynamics. By analyzing pressure (P), volume (V), and temperature (T) relationships in various weather systems, we confirmed the law’s effectiveness in modeling large scale phenomena such as cyclones and anticyclones. Specifically, it was found that low-pressure systems correlated with rising warm air, validating the direct proportionality between temperature and volume under decreasing pressure, as per the Ideal Gas Law PV=nRT, as suggested by Anthes [57]. Wallace and Hobbs [58] emphasized that the Ideal Gas Law is particularly useful in estimating air density changes at varying altitudes, which is crucial for understanding buoyancy and convective processes involved in storm formation. For instance, in simulating tornadic activity, we observed that areas of rapidly decreasing pressure corresponded to lower air density and increased uplift, supporting theoretical expectations described by Emanuel [59]. In comparative planetary analysis, the law was also applied to estimate atmospheric behaviors on Venus and Mars. Crisp [60] demonstrated that atmospheric differences mainly in composition and thermal properties cause significant deviations from ideal gas behavior, thereby reinforcing the importance of non-ideal gas models in extreme planetary environments. However, limitations were noted during high-intensity weather events such as hurricanes, where rapid and localized changes in pressure and temperature deviate from ideal conditions. Fleagle and Businger [61] pointed out that the Ideal Gas Law only offers approximations under such conditions, requiring the incorporation of more advanced, real-gas-based models for greater accuracy. The integration of machine learning with thermodynamic equations has shown promise in enhancing model precision, especially for short-term weather anomalies. Liu et al. [62] demonstrated how artificial intelligence can provide real- time corrections for deviations from ideal behavior, leading to improved forecasting and more reliable

atmospheric models.

10. 1. Datasets, Models, and Computational Tools

The simulations and analyses presented in this study were gathered from a range of meteorological datasets, thermodynamic models, and atmospheric equations referenced throughout the literature review. Real time meteorological data were used to evaluate pressure, temperature, and volume relationships in various weather systems, as discussed by Wallace and Hobbs [58] and Anthes [57]. These datasets supported the application of the Ideal Gas Law in modeling vertical air structure and buoyancy effects. Atmospheric motion and planetary comparisons were guided by thermal and compositional data referenced in Crisp [60] and Flasar et al. [11]. The Clausius-Clapeyron equation, refined with specific volume terms as shown by Huang et al. [22], was used to improve saturation vapor pressure calculations. Improved modeling frameworks, including Euler’s equations and the barotropic equation of state, were incorporated to simulate pressure, density, and temperature dynamics, as described by Makino et al. [15]. Additionally, data assimilation techniques and averaging methods discussed by Kowalski et al. [16] enhanced the representation of atmospheric states. These computational tools and models together supported the simulations presented in the results, providing a basis for analyzing gas behavior in meteorological contexts.

11. Conclusion

This research highlights the enduring significance of the Ideal Gas Law as a broad topic in meteorological science while emphasizing the need for evolution to meet modern forecasting demands. As a foundational thermodynamic model, it offers a practical framework for estimating air density, pressure gradients, and vertical motion, key factors in predicting cloud formation, storm development, and temperature driven calculations. Its simplicity and adaptability continue to make it a cornerstone in both academic instruction and operational weather modeling. However, its limitations become apparent under real world atmospheric conditions where ideal assumptions break down, particularly in high humid environments, during rapid pressure or temperature changes. These derivations can lead to significant forecasting errors, especially during severe weather events or in complex planetary atmospheres. To address these issues, the integration of artificial intelligence (AI) and machine learning (ML) provides a transformative solution by leveraging large datasets to model nonlinear relationships and correct for the Ideal Gas Law’s oversimplifications. This fusion of data driven insights with classical physics enables hybrid forecasting systems that are both adaptive and theoretically grounded. As these models continue to evolve, they promise not only to improve predictive accuracy but also to provide a deeper understanding of atmospheric dynamics, paving the way for resilient, real time and globally scalable weather forecasting systems.

• Practical Implications for Meteorology and Climate Science

The Ideal Gas Law remains a foundational tool in meteorology, offering a simplified framework for estimating air density, pressure gradients, and vertical motion key elements in forecasting cloud formation, storm development, and temperature-driven circulation. However, its assumption of ideal conditions often fails under real-world scenarios involving high humidity, rapid pressure changes, or extreme temperatures. These limitations are especially evident during severe weather events, in polluted urban environments, and in planetary atmospheres with non-Earth like compositions. In meteorology, the law’s inability to account for gas mixtures and rapid thermodynamic shifts can lead to significant forecasting errors. In climate science, it lacks the capacity to model radiation, energy balance, and long-term processes like the greenhouse effect, resulting in 5–10% buoyancy estimation errors under certain conditions (e.g., pressures below 950 hPa and lapse rates above 20 K/km). These challenges underscore the need for more advanced models that incorporate real gas behavior and corrections for non-ideal atmospheric dynamics.

• Key Findings and Future Research Directions

This study emphasized the Ideal Gas Law’s critical role in understanding atmospheric behavior, including its influence on temperature, pressure, air mass dynamics, and the formation of cyclones and tornadoes. It also explored its comparative application across planetary atmospheres and its limitations in modeling greenhouse gas effects. As meteorology evolves, integrating artificial intelligence (AI) and machine learning (ML) presents a promising path forward. These technologies can learn from observational data, detect nonlinear patterns, and correct for deviations that traditional models overlook. Future research should prioritize the development of hybrid forecasting systems that merge classical thermodynamics with data-driven algorithms. Such models will enhance predictive accuracy, improve long-term climate simulations, and support more reliable, real-time weather forecasting and climate decision-making.

References