Volume 12 - Year 2025 - Pages 417-422
DOI: 10.11159/jffhmt.2025.041
Unsteady MHD Flow of a Viscoelastic Fluid Through a Porous Medium Near an Oscillating Porous Plate
Madhumita Mahanta1, Ashis Paul2
1,2Department of Mathematics
Girijananda Chowdhury University
Hathkhowapara, Azara, Guwahati-781 017, Assam, India
madhumita_maths@gcuniversity.ac.in
Abstract - The unsteady flow of an incompressible, electrically conducting viscoelastic fluid governed by the second-order fluid model has been investigated in the presence of an oscillating infinite porous plate. The analysis is conducted under the influence of a uniform transverse magnetic field. The governing nonlinear differential equations that describe the flow dynamics are derived and solved. The effects of various physical parameters, particularly the viscoelastic parameter are examined in detail. The results are presented through graphical representations of the velocity profiles, highlighting how the viscoelasticity influences the flow behaviour in presence of the various parameters involved in the solution.
Keywords: MHD, Incompressible, Oscillatory flow, Porous medium, Viscoelastic fluid
Keywords: Force, Mass, Numerical models.
© Copyright 2025 Authors - This is an Open Access article published under the Creative Commons Attribution License terms Creative Commons Attribution License terms. Unrestricted use, distribution, and reproduction in any medium are permitted, provided the original work is properly cited.
Date Received: 2025-09-18
Date Revised: 2025-10-10
Date Accepted: 2025-10-25
Date Published: 2025-12-03
1. Introduction
The study of fluid flow through porous media has attracted considerable attention in recent years, particularly within the field of geophysical fluid dynamics. One notable geophysical application is the extraction of crude oil from the pore spaces of reservoir rocks, highlighting the practical relevance of this research. Understanding flow through permeable media is increasingly critical in modern science due to its natural occurrence and its role in diverse fields such as petroleum engineering and physiological systems. In recent decades, interest in fluid transport within porous structures has surged, driven by its vital applications in natural systems and industries like oil recovery and biomedical sciences. Fluid dynamics in porous media represents a key area of inquiry in contemporary research, fuelled by its significance in earth sciences and emerging technologies related to energy and health.
Flows through permeable media are widespread in nature, making their study essential in various scientific and engineering fields. Such flows play a crucial role in petroleum engineering for analyzing oil, gas, and water movement in reservoirs, as well as in chemical engineering for processes like filtration and water purification. They are also significant in studying groundwater resources and riverbed leakage. Although permeable media are inherently non-homogeneous, they can be approximated as homogeneous fluids with equivalent dynamic properties to simplify analysis. This allows complex flow problems to be modelled as the motion of a homogeneous fluid experiencing resistance.
The study of oscillatory flow through permeable media has drawn significant research interest because of its wide-ranging applications across science and technology. Unsteady flows are vital in chemical, mechanical, and aerospace engineering. Pande et al. [1] studied the unsteady hydromagnetic thermal boundary layer flow. In a subsequent study, Pande et al. [2] investigated the same unsteady hydromagnetic flow under the condition of no heat transfer. Furthermore, Pande et al. [3] analyzed the hydromagnetic flow in the vicinity of an oscillating porous limiting surface. Yamamoto and Iwamura [4] investigated the flow streaming into a porous and permeable medium with arbitrary but smooth wall surface. Choudhary [5] studied flow of a viscous incompressible fluid of small electrical conductivity near an infinite insulated porous flat plate oscillating harmonically in its own plane in the presence of a uniform transverse magnetic field. Raptis and Perdikis [6] studied the flow of a viscous incompressible fluid through a highly porous medium bounded by a vertical plane surface of constant temperature. Raptis [7] investigated the flow of an unsteady free convective flow of an electrically conducting fluid through a porous medium bounded by an infinite vertical and porous plate. Takhar et al. [8] examined asymmetric MHD flow past a semi-infinite moving plate, while Watanabe [9] analyzed the impact of uniform suction or injection on MHD boundary layer flow over a flat plate under a pressure gradient. Singh and Dikshit [10] focused on hydro magnetic flow past a continuously moving semi-infinite plate with strong suction. Lawrence and Rao [11] also studied MHD flow past a semi-infinite moving plate. Choudhury and Das [12] investigated non-Newtonian MHD boundary layer flow over a flat plate. Ahmed and Ahmed [13] addressed two-dimensional MHD oscillatory flow along an infinite vertical porous plate in a porous medium. Siddique and Mirza [14] explored MHD free convection of a viscoelastic fluid in a porous medium with variable permeability, heat source, and chemical reaction. Lastly, Kanaujia and Rajput [15] studied the combined effects of chemical reaction and Hall current on MHD flow through a permeable medium near an impulsively started vertical plate with constant wall temperature and mass diffusion. Verma and Singh [16] investigated magnetohydrodynamic (MHD) flow within a circular channel filled with a porous medium. Neelima et al. [17] studied flow of an incompressible viscous fluid in a permeable medium close to an infinite permeable oscillating plate in presence of a uniform transverse magnetic field. Raju et al. [18] investigated the unsteady and incompressible magnetohydrodynamic (MHD) free convection flow of a viscoelastic fluid near an infinite vertical oscillating porous plate. This investigation accounts for simultaneous heat and mass transfer processes within the flow system, which is subjected to rotational effects and influenced by a uniform transverse magnetic field. The unsteady magnetohydrodynamic (MHD) free convective oscillating flow of an optically thin incompressible viscous fluid embedded in two parallel porous walls under the influence of an externally applied transverse magnetic field with a chemical reaction has been studied by Anand Kumar et al. [19]. The study of electrically conducting fluid flows bounded by wavy walls is of significant interest due to its wide range of applications, including transpiration cooling in re-entry vehicles and rocket boosters, cross-hatching patterns on ablative surfaces, and film vaporization processes in combustion chambers. Abbas et al. [20] investigated heat transfer in oscillatory flow of a magnetized second order fluid through an asymmetric porous wavy channel, incorporating velocity slip and temperature jump conditions. Governed by a modified Darcy’s law, the flow behaviour suggests potential for enhanced thermal control, with applications in improving drug release rates and distribution.
This study examines the motion of an electrically conducting, incompressible second order fluid through a permeable medium near an infinite oscillating permeable flat plate, under the influence of a transverse magnetic field and a fixed reference frame relative to the fluid. The fluid governed by the constitutive equation [Coleman and Noll (1960)]
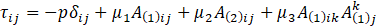
where μ1 is the shear-viscosity, μ2 is the coefficient of viscoelasticity, μ3 the coefficient of cross-viscosity and A(1)ij and A(2)ij are the Rivlin-Ericksen tensors defined as
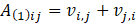
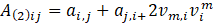
where μ2 is negative from thermodynamic consideration [Coleman and Markovitz (1964)].
2. Formulation
Let us consider the flow of an electrically conducting fluid through a porous medium of permeability k and unit porosity, bounded by a permeable plate. A uniform magnetic field H0 acts along the y-axis. For low magnetic Reynolds number Rσ, the induced magnetic field is negligible compared to the applied field. Due to the infinite extent of the plate and uniform suction, the flow depends only on y and time t, with constant fluid pressure p.
Let u and v denote the velocity components along the x and directions, respectively, relative to a permeable plate. If V represents the suction or injection velocity at the plate, the flow satisfies the following equations of continuity and momentum:
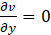
due to the suction condition at y = 0, leading to the result v = V everywhere.
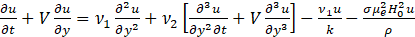
where σ is the electrical conductivity and μe the magnetic permeability, ρ the density, ν1 and ν2 are the coefficients of viscosity and elasticity respectively. The relevant boundary conditions are
u→0 for y→∞
3. Method of solution
Let us introduce the following non-dimensional variables and parameters
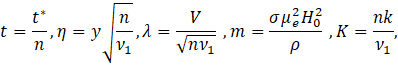
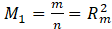
Using these and dropping *, we have from (2) and (3)
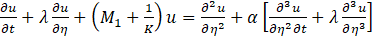
subject to boundary conditions
u→0 for η→∞
where λ is the suction parameter, M1 is the Hartmann number, Κ is the permeability coefficient of porous medium and α=(ν2 n)/ν1 is the viscoelastic parameter.
Let the solution be of the form
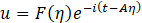
Substituting this into equation (4) and separating real and imaginary components, the following expressions are obtained
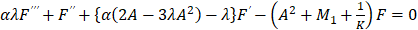
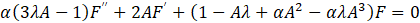
where dash denotes the derivatives with respect to η
Solving (6) and (7) together with (5), the solution for F(η) is obtained as
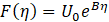
Where B is the constant of integration and
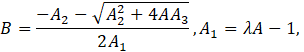
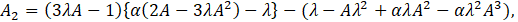
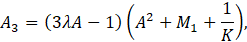
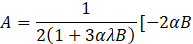
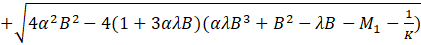
The expression for the velocity function is given by
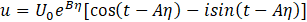
and the real and imaginary parts are
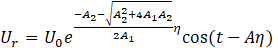
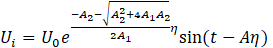
4. Results and Discussion
The purpose of the present study is to investigate the influence of viscoelastic properties on the behaviour of an unsteady magnetohydrodynamic (MHD) flow of a viscoelastic fluid through a porous medium in the vicinity of an oscillating porous plate. Specifically, the study aims to analyze how the interplay between magnetic fields, fluid elasticity, porosity and oscillatory boundary motion affects the velocity distribution. The study aims to highlight the impact of the viscoelastic parameter α on flow characteristics. The viscoelastic effects are represented by the non-dimensional parameter α, and results for Newtonian fluids can be retrieved by setting α=0. Notably, these results are consistent with those reported by Neelima et al (2022).
The suction parameter plays a vital role in controlling and stabilizing fluid flow. Its influence is particularly significant in engineering and geophysical applications, where suction is employed to stabilize the flow, reduce boundary layer thickness, and suppress instabilities induced by unsteadiness, viscoelasticity, and magnetic field interactions. By modulating the suction rate, it becomes possible to enhance flow control, improve heat and mass transfer characteristics, and mitigate adverse effects such as flow separation or oscillatory disturbances.
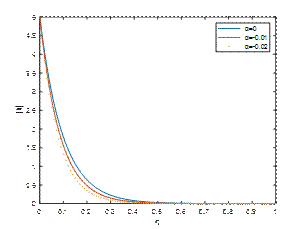
M1=2, Κ=2, t=𝜋/2and λ=1
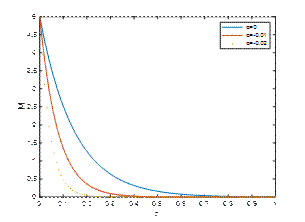
M1=2, Κ=2, 𝑡=𝜋/2and λ=5
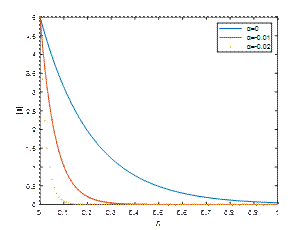
M1=2, Κ=2, 𝑡=𝜋/2and λ=10
Fig. 1, Fig. 2 and Fig. 3 reveal |𝑢| against η for M1=2, Κ=2, 𝑡=𝜋/2 and λ=1,5,10 respectively. It is observed that the velocity of the fluid is diminished with a rise in the absolute value of the viscoelastic parameter α. An increase in the suction parameter λ enhances the velocity profile in the Newtonian case due to the thinning of the boundary layer and improved momentum diffusion. However, in non-Newtonian fluids, particularly shear-thinning types, an increase in suction tends to suppress the velocity profile, as the nonlinear rheology counteracts the boundary layer thinning effect.
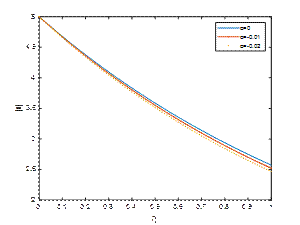
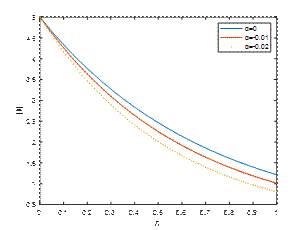
λ=5, Κ=2, 𝑡=𝜋/2and M1=10
λ=5, Κ=2, 𝑡=𝜋/2and M1=15
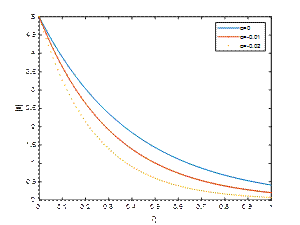
λ=5, Κ=2, 𝑡=𝜋/2and M1=20
The Hartmann number M1 is a dimensionless parameter that characterizes the influence of a transverse magnetic field on a conducting fluid. The magnetic field suppresses oscillations and fluctuations, acting as a stabilizing agent in unsteady viscoelastic flows. Fig. 4, Fig. 5 and Fig. 6 demonstrate |𝑢| against η for Κ=2, λ=5,𝑡=𝜋/2 and M_1=10,15,20 respectively. It is observed that the velocity of the fluid decreases with the rise in the absolute value of the viscoelastic parameter α. The velocity profile is observed to be diminished with the increase of the magnetic field parameter M1.
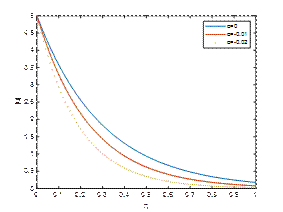
M1=2, λ=5, t=𝜋/2and Κ=0.2
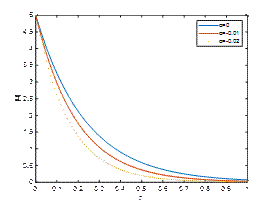
M1=2, λ=5, 𝑡=𝜋/2and Κ=0.7
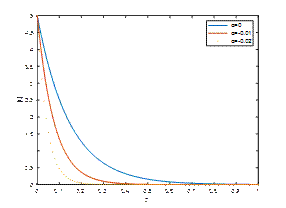
M1=2, λ=5, 𝑡=𝜋/2and Κ=2
The permeability coefficient of the porous medium is another key parameter in analyzing the behaviour of the flow. The porous medium resists the flow. A decrease in permeability enhances the drag within the medium, leading to a reduction in fluid velocity and suppression of oscillatory effects of the unsteady MHD flow near the oscillating porous plate. Fig. 7, Fig. 8 and Fig. 9 depict |𝑢| against η for M1=2, λ=5, 𝑡=𝜋/2 and Κ=0.2,0.7,2 respectively. The figures reveal that the velocity of the fluid is diminished with the increase of the absolute value of the viscoelastic parameter α. The decreasing trend in the velocity profile is observed with the increase of porous medium parameter Κ.
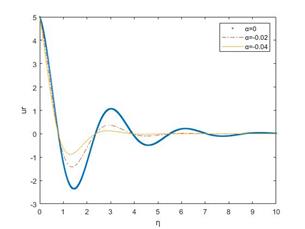
M1=2, K=2, A=6, λ =5, 𝑡=𝜋/2
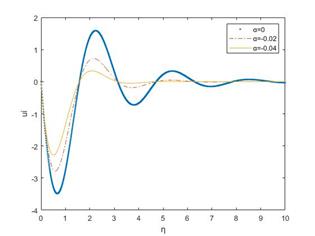
M1=2, K=2, A=6, λ =5, t=𝜋/2
As η increases, Fig 10 and Fig 11 show an oscillatory decay, i.e., the amplitude of oscillations decreases with increasing η, tending toward zero. In both the real and imaginary parts of the velocity profile, it is observed that they increase as the viscoelastic parameter α increases together with an oscillatory decay. The flow becomes less oscillatory and approaches zero more rapidly, possibly indicating viscous dissipation. Similar trends were observed for various values of the parameters involved in the solution, further validating the influence of the viscoelastic parameter α on the flow characteristics.
5. Conclusion
In the study (Neelima et al 2022), an attempt is made to investigate the motion of an electrically conducting, incompressible and viscous fluid through a porous medium near an infinite, oscillating, permeable flat plate under the influence of a transverse magnetic field and stationary with respect to the fluid. Results are computed introducing non-dimensional parameters. Understanding these effects is crucial for optimizing industrial processes such as polymer processing, oil recovery and biomedical applications, where such complex flow environments are common
The results of investigation may be summarized in the following conclusions:
- Velocity retardation occurs in both Newtonian and non-Newtonian fluid flows
- The velocity profile is observed to be diminished with the increase of the suction parameter, magnetic field parameter and the porous medium parameter
- Both the real and imaginary components of the velocity function exhibit oscillatory decay
References
[1] G. C. Pande, N. G. Kafousias and C. L. Goudas, Unsteady hydro magnetic thermal boundary layer flow, Astrophys. Space Science 45 (1976), 397-410. View Article
[2] G. C. Pande, N. G. Kafousias and C. L. Goudas, Unsteady hydromagnetic thermal boundary layer flow II, no heat transfer, Astrophys. Space Science 50 (1977), 141-152. View Article
[3] G. C. Pande, N. G. Kafousias, G. A. Georgantopoulos and C. L. Goudas, Hydromagnetic flow near an oscillating porous limiting surface, Astrophys. Space Science 51 (1977), 125-134. View Article
[4] K. Yamamoto and N. Iwamura, Flow with convective acceleration through a porous medium, J. Engg. Math. 10 (1976), 41-54. View Article
[5] R. C. Choudhary, Hydromagnetic flow near an oscillating porous flat plate, Indian Acad. Sci. A 86 (1977), 531-535. View Article
[6] A. Raptis and C. P. Perdikis, Oscillatory flow through a porous medium by the presence of free convective flow, International Journal of Engineering Science, 23 (1985), 51-55. View Article
[7] A. Raptis, Flow through porous medium in the presence of magnetic field, Int. J. Energy Res. 10 (1986), 97-100. View Article
[8] H. S. Takhar, A. A. Raptis and C. P. Perdikis, MHD asymmetric flow past a semi-infinite moving plate, Acta Mechanica 65(1-4) (1987), 287-290. View Article
[9] T. Watanabe, Effect of uniform suction or injection on a magneto-hydrodynamic boundary layer flow along a flat plate with pressure gradient, Acta Mechanica73 (1988), 33-44. View Article
[10] A. K. Singh and C. K. Dikshit, Hydromagnetic flow past a continuously moving semi-infinite plate at large suction, Astrophys. Space Sci. 148 (1988), 249-256. View Article
[11] P. S. Lawrence and B. N. Rao, Magneto hydrodynamic flow past a semi-infinite moving plate, Acta Mech. 117 (1996), 159-164. View Article
[12] R. Choudhury and A. Das, Magneto-hydrodynamic boundary layer flows of non-Newtonian fluid past a flat plate, Indian J. Pure Appl. Math. 31(11) (2000),1429-1441.
[13] S. Ahmed and N. Ahmed, Two dimensional MHD oscillatory flow along a uniformly moving infinite vertical porous plate bounded by porous medium, Indian J. Pure Appl. Math. 35(12) (2004), 1309-1319.
[14] Imran Siddique and Itrat Abbas Mirza, Magneto-hydrodynamic free convection flows of a viscoelastic fluid in porous medium with variable permeability heat source and chemical reaction, Results in Physics 7 (2017), 3928-3937. View Article
[15] Neetu Kanaujia and Uday Singh Rajput, Combined effect of hall current and chemical reaction on MHD flow through porous medium with heat generation past an impulsively started vertical plate with constant wall temperature and mass diffusion, Summer and Autumn 9(1) (2019), 121-132.
[16] Vineet Kumar Verma and Sanjeeva Kumar Sing, Magnetohydrodynamic flow in a circular channel filled with a porous medium, Journal of Porous Media18(9) (2015), 923-928. View Article
[17] A. Neelima and V. Omeshwar Reddy, Magnetohydrodynamic flowthrough a porous medium bounded by an oscillating porous plate, Advances and Applications in Fluid Mechanics 28 (2022), 27-40. View Article
[18] G. Raju, B. Hari Babu and L. Rama Mohan Reddy, MHD convective rotating flow of viscoelastic fluid past an infinite vertical oscillating porous plate with Hall effects, 52(3), (2022), 2139-2141 View Article
[19] S. Abhilash Anand Kumar, S Sreedhar and M Veera Krishna, Heat and mass transfer on unsteady MHD convective flow through porous medium between two vertical plates with chemical reaction, The Journal of Process Mechanical Engineering, 238 (4), (2023), 1665 - 1675 View Article
[20] Z. Abbas, Q. Izhar, M.Y. Rafiq and A. Ali, Thermally oscillatory flow inside an irregular channel through a porous medium with velocity and temperature slips, Case Studies in Thermal Engineering, 60, (2024), 104646 View Article

