Journal of Fluid Flow, Heat and Mass Transfer (JFFHMT)

ISSN: 2368-6111

Electrokinetic Regulation of the Transfer Process in the Hydraulic System in Microchannels

Fuad Veliyev¹, Elshan Aliyev², Aida Aslanova¹

¹Baku Higher Oil School
Yeni Salyan Highway 3rd km, Baku, Azerbaijan
²Azerbaijan State Oil and Industry University,
Azadlig ave., Baku Azerbaijan
fuad.valiyev@bhos.edu.az; aida.soltanova@bhos.edu.az

Abstract - Studies have been conducted on rheophysical phenomena that occur when a viscous fluid flows through variously opened microcracks. The role of electrokinetic factor in the manifestation of the nonlinear rheological effect in a water flow in a microchannel model – the transformation of a Newtonian fluid into a non-Newtonian one – is examined experimentally. The effect of the electrokinetic potential on the intensity of the mass transfer process in the liquid–microchannel system has been studied based on the plotting of pressure recovery curves (PRC). It is established that by reducing the electrokinetic potential of the system it is possible to significantly enhance mass transfer processes and improving filtration characteristics in microchannels.

Keywords: electrokinetic factor, micochannel, rheophysical phenomena, openness, pressure recovery curves.

© Copyright 2025 Authors - This is an Open Access article published under the Creative Commons Attribution License terms Creative Commons Attribution License terms. Unrestricted use, distribution, and reproduction in any medium are permitted, provided the original work is properly cited.

Date Received: 2025-06-16
Date Revised: 2025-07-02
Date Accepted: 2025-07-30
Date Published: 2025-xx-xx

1. Introduction

Microchannels are one of the most important elements for liquid transportation in microsystem technologies, and therefore, the study of the patterns of fluid movement in subcapillary pores and microcracks is of essential scientific and practical interest.

Microfluidic technologies are increasingly used for applications that require precise fluid control, such as water purification, biomedical diagnostics, and chemical reactions. For example, in microreactors and filtration devices, understanding the factors that control fluid flow and mass transfer can significantly enhance system performance by improving efficiency and reducing the chances of clogging or flow anomalies.

According to the results of a number of experimental studies, a viscous liquid during flow in low-permeability reservoirs exhibits an abnormal non-Newtonian character, accompanied by a violation of the linearity of the filtration process, and, accordingly, Darcy's law [1, 2]. It has been established that the flow of Newtonian liquids (water, light oil) in microcracks, at certain small values of their openness, becomes non-Newtonian, with the manifestation of an initial pressure gradient and flow locking [3].

At microscale levels, fluids such as water or oil often exhibit non-Newtonian behavior, where the flow characteristics deviate from traditional Newtonian fluid behavior (i.e., a linear relationship between shear stress and shear rate). Non-Newtonian characteristics become particularly apparent in microchannels with narrow dimensions, where electrostatic interactions between the fluid and the channel walls can alter the flow properties. This is mainly due to the formation of an electric double layer (EDL) at the fluid-solid interface, which impacts the apparent viscosity and flow behavior. In narrow channels, especially those with dimensions smaller than the EDL thickness (typically on the order of micrometers), electrokinetic effects become significant and can introduce additional resistance to fluid flow.

Recent studies have explored how these electrokinetic effects influence fluid dynamics in microfluidic systems. In [4], it is demonstrated that when the channel dimensions are comparable to the EDL thickness, electrokinetic forces lead to an increase in apparent viscosity and a transition from Newtonian to non-Newtonian behavior. This transition can significantly impact the efficiency of mass transfer processes, especially in filtration and mixing applications. [5] further investigated the electrokinetic effects in microchannels and found that, at certain conditions, electrostatic interactions contribute to the development of yield stress in the fluid, preventing it from flowing unless the stress exceeds a critical threshold.

However, to date, there is no consensus on the mechanism of these phenomena, although there are various approaches to explain the abnormal hydrodynamic behavior of liquids during flow in a poorly permeable porous medium and microcracks.

Two substances with varying permittivity in contact are known to be charged along the contact surface in accordance with the Koehn rule [6]. This rule states that an electric double layer (EDL) with a specific electrokinetic potential forms on the boundary surface when liquid-solid contact takes place. Considering the diffusion layer, the EDL's thickness can range from a few microns to several microns. The EDL's electric field has an impact on the flow's characteristics in the boundary zone. This effect is negligible for channels (pipes) with sufficiently wide transverse dimensions in relation to the flow. However, the situation changes significantly for small-diameter tubes and narrow slits where the transverse dimensions match those of EDL. In this case, the electrostatic field of the EDL becomes an additional element of hydraulic resistance.

Electrokinetic potential refers to the electrical potential that forms at the fluid-solid interface due to the movement of charged particles in the electric double layer. This potential can introduce additional resistance to fluid flow, particularly in microchannels. Reducing the electrokinetic potential in a fluid system has been identified as an effective strategy for enhancing flow characteristics and mass transfer efficiency [7].

One promising approach to reducing electrokinetic potential involves the use of antistatic additives, which can alter the electrical properties of the fluid and reduce the electrostatic interactions between the fluid and the channel walls. [8] investigated the use of surfactants and antistatic agents in microfluidic systems and found that they could significantly reduce the electrokinetic potential, thereby improving the fluid flow and enhancing mass transfer rates.

In [9], the role of the electrokinetic factor in the manifestation of nonlinear rheophysical effects in rectangular microchannels was considered. It was found that the hydraulic characteristics of the flow in thin channels significantly depend on the electric potential of the flow and by reducing it, the hydrodynamic parameters of the flow can be significantly improved.

This study aims to address this gap by investigating the effect of electrokinetic potential on the mass transfer process in microcracks, specifically focusing on the role of antistatic additives like ND-12 in reducing the electrokinetic potential and improving filtration characteristics. The study will explore the impact of reducing electrokinetic potential on pressure recovery curves (PRC), mass transfer intensity, and fluid flow behavior in microchannels with slit openness ranging from 10 µm to 25 µm. By examining these factors, the research seeks to understand the transition from Newtonian to non-Newtonian behavior in microcracks, with the goal of improving filtration and mass transfer efficiency in microfluidic systems.

The findings of this study will provide valuable insights for optimizing microfluidic device design, especially for applications where precise fluid control is required. Understanding how electrokinetic potential influences the flow and filtration characteristics in confined spaces like microcracks will contribute to the development of more efficient and reliable microfluidic technologies, with applications in fields such as water purification, biomedical diagnostics, and microreactor design.

2.Methodology

The experiments were carried out on a rectangular micro-crack model with a length of 30 cm and a width of 4 cm, which was formed by two parallel plates of smooth stainless steel with a thickness of 4 cm. Microcracks of a certain openness (h) were obtained by installing non-wettable gaskets of appropriate thickness between the plates.

The experiments were carried out atdifferentvalues of the slit openness in the range of 10÷25microns.Toensure the isothermicity of the process, the model was installedin a thermowell,which was connectedto an ultrathermostat. The pressure was measured by high-precision manometers installedat the inletandoutlet of the model (Figure 1).

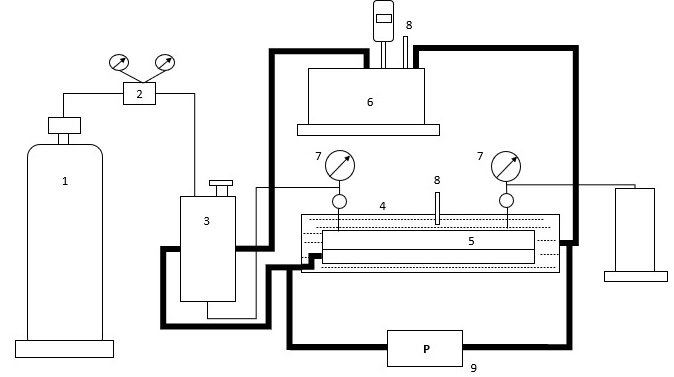
Figure 1. Experimental setup:

1-high pressure gas cylinder, 2-regulating conductor, 3-container, 4-thermo-bath, 5-microcrack model, 6-thermostat, 7-pressure gauge, 8 - thermometer, 9-potentiometer

To regulate the electrostatic potential of the flow, it was decided to use antistatic additives. ND-12 reagent was used as an antistatic agent, which is usually used as a demulsifier in oilfield conditions.

The ND-12 reagent has sufficient surface activity, dissolves well in water, is inert to metals, does not change its properties with changes in the conditions of the process (temperature, pressure), and is economically efficient. The physical properties of the ND-12 reagent are presented in Table 1.

Table 1. Physical properties of ND-12 reagnet

External appearance	Clear flowing liquid from light to light yellow
Density at 20℃ , kg/m3	910-980
Freezing temperature ℃	-50
Hydrogen indicator of the medium, pH	7-9
Kinematic viscosity, sSt	25-30
Solubility	Dissolved in water and oil

To build pressure recovery curves, the input of the microcrack model was adjusted to a pressure of 4*10⁵ Pa, and the output to a pressure of 10⁵ Pa. After stabilizing the flow in the model, the output of the model was closed and the pressure was recorded during recovery. During this time, the input pressure of the model was kept constant at 4*10⁵ Pa.

The process was repeated at four different openness of the slit of the model– 10 µm, 15 µm, 20 µm, and 25 µm – and pressure recovery curves were constructed.

Experimental results

At the beginning, to determine the optimal concentration of additives, measurements of the electrode potential were carried out using an electrostatic cell, which is a stainless steel cell filled with used water with a platinum electrode dipped into it. The second electrode was the body of the cell.

Drops of reagent were added to the water, and using a microvoltmeter, the values of the potential ∆ϕ were taken at various concentrations.

The Figure 2 shows the dependence of the electrode potential on the concentration of the antistatic reagent. As can be seen, this dependence is not monotonous and the minimum potential is achieved at very small addition of the reagent. The potential first falls as the concentration rises, but after reaching a minimum, it starts to rise to a maximum value and then essentially stays the same at greater additive concentrations.

It was found that the optimal concentration value at which the minimum potential is reached is approximately 0.0060% (60ppm).

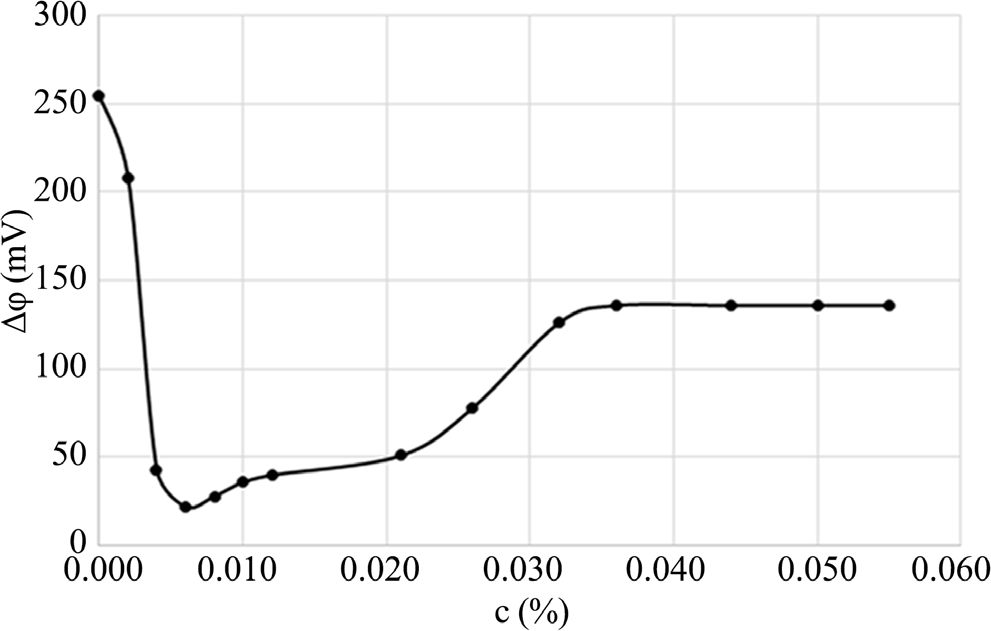
At this concentration, there is a multiple (more than 10-fold) decrease in potential. A further increase in concentration is accompanied by an increase in ∆ϕ, the value of which remains almost unchanged at concentrations greater than 0.032% (320ppm).

The effect of the electrokinetic potential on the intensity of the mass transfer process in the liquid–microchannel system has been studied based on the plotting of pressure recovery curves (PRC).  

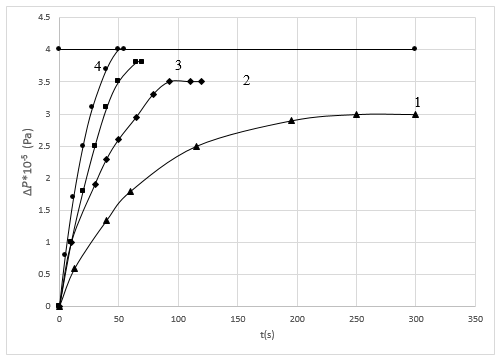
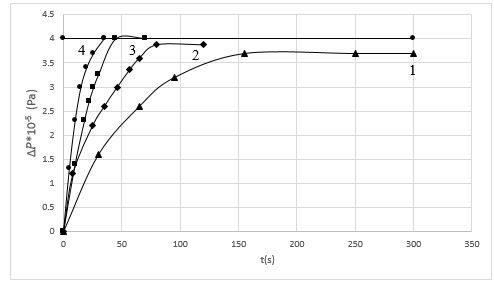
Figure 3 and 4, represent PRCs at four different openness for water in the absence and presence of the optimum concentration of the additive. From PRCs it is clear that during the flow of water through the microcrack model, starting from h_kr, the pressure recovery time and relaxation time increase with the decrease of openness h.

For comparison, for water without additives at an opennness of the slit of the model of 10 µm and water with additives of 60 ppm, at a temperature of 30^oC, the characteristic γ=γ(τ) curves are shown (Figure 5).

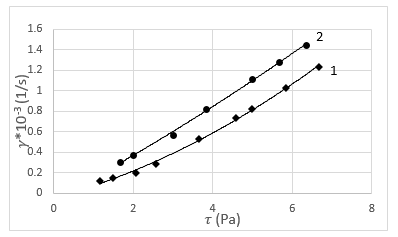
From the comparison, it can be seen that with a reduced electrical potential of the system, the pressure in the microchannel is set at a faster rate, which indicates an increase in the intensity of the mass transfer process in the system, and, accordingly, an improvement in the filtration characteristics of the microcrack.

With steady water movement, using a microvoltmeter connected to the input and output of the model, the stream potential Δφ in the model was determined, on its various openness (h - 10 µm, 15 µm, 20 µm and 25 µm). In Figure 6, the corresponding dependences Δφ=Δφ(h) for the flows of tap water and water with an antistatic additive (60 pm) are presented.

Figure 6. The dependence of the ∆φ on the value of the openness h: 1 – water with an additive of 60 ppm, 2 – water with an additive of 400 ppm, 3 – water without an additive

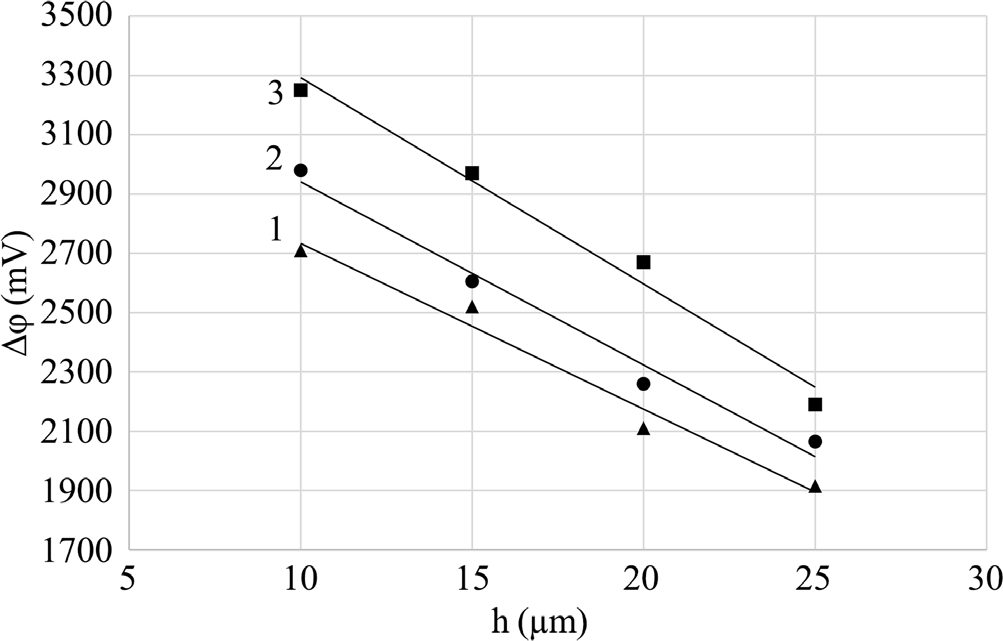
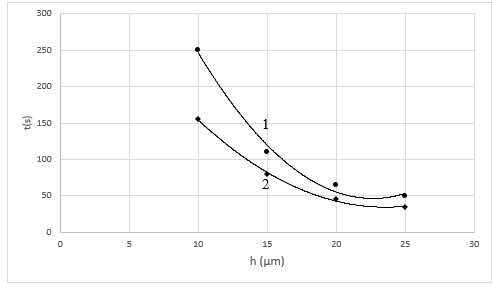
Figure 7 shows the dependences of the pressure recovery time in the microchannel on its openness τ=τ(h) in the absence and presence of an antistatic additive in water.

Figure 7. Dependence of pressure recovery time on the openness h: 1- water without antistatic additive, 2 –water with an antistatic additive of 0.006%.

4. Discussion

The article represents the results of experimental work of the study of the effect of reducing the electrokinetic potential of hydraulic systems on the intensity of transmission processes in the microcrack model. The effect of reducing the electrokinetic potential in water-microcrack system on the pressure recovery process was evaluated in detail.

Firstly, pressure recovery curves (PRC) were extracted in various openness of the silt of the microcrack model.

It is revealed that there is a critical value of the openness of the gap (h_cr) at which the non-Newtonian nature of the system is manifested and the pressure at the outlet of the model is set at a level below the input pressure, which indicates the appearance of a yield shear stress (τ₀) in the system.

It has been established that during the flow of water from the microcrack model, starting from the h_kr, as the openness of the slit decreases, the pressure increases during recovery. While the pressure at 25µm openness of the slit was 50 s during recovery, at 10µm openness it rose to 250 s (Figure 3).

At the same time, a complete restoration of pressure at the entry and exit points of the microchannel is recorded at the values of h h_kr. However, as h decreases, the difference in pressures at the entry and exit points is manifested, reaching a peak value at the smallest value of h in the considered range (h=10 µm). This process can be explained by the manifestation of electrokinetic factors, as well as the EDL effect at the openness below h_kr and its intensification as h decreases. Consequently, a Newtonian fluid makes a transition to a non-Newtonian fluid, and as h decreases, the non-Newtonian properties of the fluid flow become sharper.

An important result of the experiments is that reducing the potential of the system by an antistatic additive to water significantly increases the intensity of the pressure recovery process in the microcrack model. Thus, the recovery time of the pressure at h=10µm for water without additives was 250s, while with the effect of the optimal concentration of the additive, it is 150s. In the considered range, similar intensification in the pressure recovery process was recorded at other values of h (from the comparison of Figures 3 and 4).

Under the influence of the antistatic additive, a decrease in the difference in settled pressures manifested at the entry and exit points of the model was also recorded at values below h_kr. At the smallest value of openness (h=10µm) in the range under consideration, the difference in settled pressures during pressure recovery for water without additives was 1 atm, with the effect of the optimum amount of additive this value was 0.3 atm (from the comparison of Figure 3 and 4).

At the openness of the slit h=20µm, when restoring the pressure for water without additives, a pressure difference of 0.2 atm was obtained, due to the optimal amount of the additive, a complete restoration of the pressure was provided throughout the model, which is an indicator that the water has already regained its Newtonian liquid characters.

The recorded results are also consistent with the tendency of the flow potential to change under the influence of the antistatic additive. In the considered range, a decrease in the flow potential by up to 1.3 times was recorded due to the optimal concentration of the antistatic additive, which results in a decrease in pressure recovery time by up to 2 times in the corresponding openness (Figure 6).

These results are fully consistent with the final conceptual conclusions established on the role of the electrokinetic factor in this process, transforming water into a non-Newtonian liquid in microcrack of a certain size on the basis of γ=γ(τ) curves (Figure 5).

It is also clear from Figure 7 that, in a considered range of openness of the slit, pressure recovery time is significantly reduced with the presence of the optimal concentration of the antistatic additive and the effect is getting stronger towards the lowest value of the openness.

Consequently, it was found that reducing the electrokinetic potential of the fluid flow has a significant effect on the intensity of non-stationary processes. Thus, by reducing the electrokinetic potential of the hydraulic system, the rheophysical transmission process in the system intensifies, and as a result, the pressure recovery time in the hydraulic system is significantly reduced.

5. Conclusion

With an emphasis on the transition of a Newtonian fluid into a non-Newtonian fluid under varied operating conditions, this study investigates the effects of electrokinetic potential on the mass transfer processes and filtration properties in microchannels. Experimental results have shown that it is possible to significantly increase the intensity of mass transfer and pressure recovery processes by decreasing the electrokinetic potential. In microchannels, particularly at smaller openness of the slit, the application of antistatic additives, particularly ND-12, has demonstrated efficacy in reducing the electrokinetic potential, improving the filtering properties and speeding up the pressure recovery process.

Reducing the electrokinetic potential of the fluid flow with the addition of antistatic additives has a significant effect on the intensity of non-stationary processes. In the absence and presence of antistatic additives, from the comparative analysis of pressure recovery curves in microchannel of different sizes it is clear that with a decrease in the electrical potential, the rheophysical transmission process in the system intensifies and, as a result, the pressure relaxation time in the hydraulic system is significantly reduced.

It is revealed that in the absence of an antistatic additive in water h_cr = 25µm, whereas in the presence of an additive, h_cr decreases to 20 microns.

From the comparison of the curves, it is also revealed that residual pressure difference between inlet and outlet of the microchannel decreases significantly as a result of decrease of electrokinetic potential of the system.

As can be seen, a decrease in the electrical potential leads to a decrease in the pressure recovery time, and the effect increases with a decrease in h, reaching maximum expressiveness at a smallest h.

These findings have important ramifications for applications in microsystem technologies where effective filtration and fluid flow optimization are essential. In addition to improving mass transfer processes, reducing the electrokinetic potential also controls the fluid's transition from Newtonian to non-Newtonian behavior, improving performance in small spaces. This work emphasizes how electrokinetic regulation can be used to enhance the construction and functionality of microfluidic devices, especially in applications involving the manipulation and filtering of fluids on a tiny scale.

Several potential directions for future research may expand on these findings. First, a more detailed study on the long-term stability of antistatic additives under different flow conditions might be useful to improve the understanding of how reliable this technique is in practice. Also, the influence of various microchannel geometries (e.g. changes in aspect ratio and in surface roughness) on the electrokinetic behavior of the solution needed to be investigated for an optimized microchannel geometry for various applications. Lastly, using this approach in the context of application to the blood filtration, environmental monitoring or chemical processing, etc. could be a way to proof a scalability and usefulness for implementation in industry.

In summary, by adjusting the electrokinetic potential, the report offers a viable method for improving mass transfer and filtration properties in microchannels. Future advancements in the design of microfluidic devices are made possible by this technology, which has potential uses in a variety of scientific and industrial domains.

References