Journal of Fluid Flow, Heat and Mass Transfer (JFFHMT)

ISSN: 2368-6111

Coherent Dynamics of Liquid Jet Breakup in Annular Crossflow

Deepak Kumar¹, Abhijit Kushari¹

¹Department of Aerospace Engineering, India Institute of Technology Kanpur
Kalyanpur, Kanpur, Uttar Pradesh, India

Abstract - The primary breakup characteristics of a liquid jet injected radially into an annular air crossflow are experimentally investigated under atmospheric conditions at a fixed air Mach number of 0.12. The liquid injection velocity is varied from 1.417 m/s to 7.084 m/s through a 1 mm orifice, yielding liquid-to-air momentum flux ratios in the range of 1 to 25. High-speed imaging at 3000 frames per second is employed to capture the transient spray dynamics, and a dataset of 3000 images is analyzed using Proper Orthogonal Decomposition to extract coherent flow structures and quantify the energy content of dominant modes. The results indicate that at low 𝑞, the breakup process is governed by strong shear-layer instabilities, leading to early transition to turbulence. In contrast, higher q values exhibit a delayed onset of turbulence, dominated by persistent vortex roll-up and jet penetration. The POD energy spectra reveal that the first ten modes capture the most significant coherent structures, while temporal coefficients demonstrate a clear transition from crossflow-driven to self-excited turbulent breakup as liquid to air momentum flux ratio increases.

Keywords: POD, Jet in Cross-flow, High speed imaging, Primary breakup

© Copyright 2025 Authors - This is an Open Access article published under the Creative Commons Attribution License terms Creative Commons Attribution License terms. Unrestricted use, distribution, and reproduction in any medium are permitted, provided the original work is properly cited.

Date Received: 2025-02-24
Date Revised: 2025-05-26
Date Accepted: 2025-06-16
Date Published: 2025-07-04

1. Introduction

The primary breakup of a liquid jet in crossflow is a fundamental phenomenon encountered in a variety of applications, including air-breathing propulsion systems, liquid rocket engines, diesel and spark-ignition engines, and agricultural sprays. In gas turbines and internal combustion engines, fuel injection in the form of fine droplets plays a critical role in combustion efficiency, emission reduction, and overall performance. Atomization increases the surface area of the fuel, directly impacting evaporation rates, air-fuel mixing, and NOx emissions. A thorough understanding of liquid breakup mechanisms is therefore essential for optimizing spray formation, vaporization dynamics, and combustor performance. A central objective in modern combustion systems is to reduce NOx emissions by avoiding local hot spots and promoting homogeneous, lean premixed combustion. Achieving this goal requires precise control of fuel placement and droplet size distribution, which in turn depends on the underlying breakup mechanisms. In crossflow configurations, liquid jets exhibit complex interactions with the surrounding gas stream, influencing penetration, dispersion, and the development of coherent structures. These dynamics are also vital for validating high-fidelity Computational Fluid Dynamics models and enhancing predictive design tools for injectors.

Despite extensive research, several challenges persist in understanding primary breakup transitions, especially under varying momentum flux ratios. The application of advanced diagnostic techniques and data-driven analysis tools, such as Proper Orthogonal Decomposition, provides new avenues for uncovering dominant flow structures and turbulence-induced breakup mechanisms. This study investigates the breakup dynamics of a liquid jet in an annular crossflow using POD to identify the most energetic structures and their role in the transition from jet-like to crossflow-dominated breakup across varying conditions.

2. Related Work

Over Wu et al. [1] examined the penetration and surface breakup processes of liquid jets in crossflow, showing that the liquid column consistently fractured at a fixed streamwise location. They related the breakup behavior to drag coefficients and secondary droplet disintegration times. Complementing this, theoretical and experimental studies [2] analyzed axisymmetric wave-induced jet disintegration. Wu et al. [3] measured droplet size, velocity, and flux distributions, revealing a layered droplet profile and non-uniform mass distribution at high momentum flux ratios.

Building upon this, researchers have classified breakup regimes into bag, multimode, and shear breakup [3–5], drawing analogies to secondary droplet breakup behavior. Wu et al. [1] proposed a breakup map based on the Weber number and momentum flux ratio, noting a constant cross-stream breakup location but a streamwise dependence on momentum. Mazallon et al. [4] introduced the influence of the Ohnesorge number and refined the breakup regime classification. Sallam et al. [6] further identified regime transitions and characterized ligament formation and breakup time scales.

High-speed and supersonic crossflow conditions were explored by Kush and Schetz [7], who identified breakup regimes based on the momentum flux ratio (q). They observed that wave instabilities, droplet shedding, and ligament formation dominate at different q values. Ingebo [8] attributed the wave-induced breakup to capillary and acceleration waves. Momentum balance analysis by Schetz and Padhye [9] predicted penetration heights correlating with q, while Nejad and Schetz [10] demonstrated that surface tension minimally affects penetration but significantly influences breakup characteristics.

Advanced optical diagnostics have further refined our understanding. Chen et al. [11] used Mie scattering and PIV to capture jet trajectories and boundary layer interactions. Thomas and Schetz [12] analyzed size and flux distributions in supersonic sprays, while Sankarakrishnan and Sallam [13] described droplet formation mechanisms governed by Rayleigh-Taylor instabilities during bag breakup.

Beyond experimental observations, the use of signal processing techniques such as Proper Orthogonal Decomposition (POD) has gained prominence. Lumley [14] introduced POD to fluid mechanics for identifying coherent structures in turbulence. Sirovich [15] later formulated the snapshot POD method, which efficiently decomposes flow snapshots into orthogonal modes. Bernero and Fiedler [16] applied POD to PIV data to understand spray structures, and recent studies [17] have extended this approach to breakup analysis. For instance, Kumar et al. [18] studied the primary breakup behavior of a liquid jet in an annular passage under crossflow conditions, highlighting the influence of geometry and air-to-liquid momentum imbalance. Further research by the same group [19,20] examined the effects of swirling crossflow and elevated pressure on jet trajectory and droplet dynamics, revealing significant modifications in breakup modes and droplet size distribution. These studies provide a critical foundation for understanding the breakup mechanisms presented in the current work, particularly under moderate Weber number and varying momentum flux ratio conditions.

These developments underscore the importance of combining advanced diagnostics and modal decomposition tools to uncover the physics of jet breakup. The present study leverages POD to investigate the flow field of a liquid jet in annular crossflow, aiming to quantify coherent structures and link them to different breakup regimes as a function of momentum flux ratio.

3. Experimental setup and Methodology

The test section consists of a high-pressure chamber having a glass tube fixed at the centre which has an inner stainless-steel tube with 1 mm diameter orifice.  The water from the water supply system injected perpendicular to the free stream of air through 1 mm diameter orifice. The water supply system consists of a steel water tank filled with water. The water is pressurized from the air compressor. The air from the blower goes to settling chamber via flexible steel tube. Thereafter it goes to the main test section through an iron pipe. The air inlet velocity is measured using a pitot tube fixed above the swirl vane. The pitot tube is then connected to a micro manometer to display air velocity and record the measured velocity with the help of LabVIEW program. To measure the inlet temperature, a thermocouple is fixed in a steel pipe at some distance above from the swirl vane. One gage pressure sensor is connected to the upper lid of high-pressure chamber to measure and indicate the static pressure of pressure chamber and other is connected to the iron pipe to measure and indicate static pressure of flow. The water from the outlet of tank flow through turbine flow meter to measure volume flow rate of water. The required flow rate of water is controlled by controlling tab and flow regulator. The pressure inside the water tank is control by the pressure knob. A dial gauge is used to control and monitor the pressure of the tank. The air stream

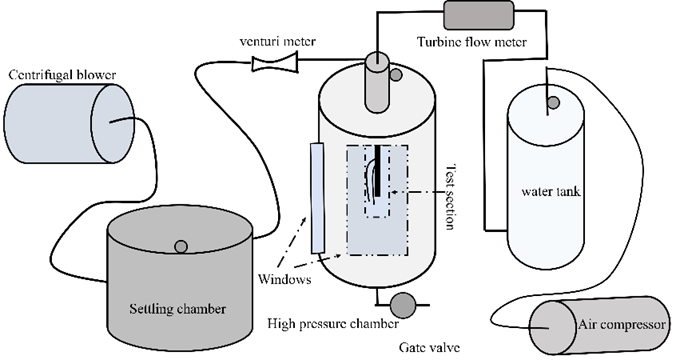
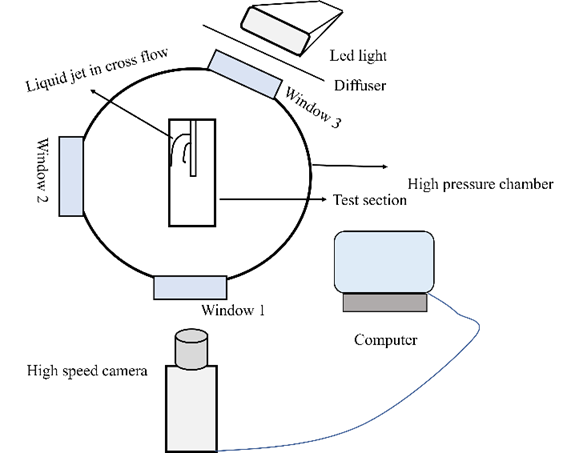
interacts with horizontally injected water jet. It bends and breaks jet into large number of ligaments and droplets of different sizes. The breakup phenomenon occurring in the test section is done by high-speed imaging. The high-speed imaging setup is illustrated in Figure 2. An LED light source equipped with a diffuser provides uniform illumination over the spray region. A Phantom V341 high-speed camera (4-megapixel resolution) is employed to capture the liquid jet in crossflow. Imaging was conducted using a back-scattering illumination technique at a frame rate of 3000 fps with an exposure time of 40 µs.

3.1. Test Conditions

All experiments were performed at room temperature using water as the working fluid. The liquid jet was horizontally injected through a 1 mm diameter orifice perpendicular to a vertical crossflow of air. The inlet air temperature was maintained at 303 K. The momentum flux ratio (q) was varied from 3 to 25, while the air inlet velocity was kept constant at U∞ =42 m/s, corresponding to a Mach number of 0.12. Under atmospheric conditions, the air density was ρ=1.16 kg/m³, resulting in an aerodynamic Weber number of 28 (based on jet diameter), and an air Reynolds number of 45,246 (based on a passage height of 17.5 mm). The corresponding air mass flow rate was m =0.1044 kg/s.

With constant air velocity, the water jet velocity was varied from 1.4 to 7.1 m/s as q increased, corresponding to a volumetric flow rate range of 65–336 mL/min. As a result, the liquid Reynolds number varied from approximately 1417 to 7074, and the liquid Weber number ranged from 28 to 698. The Ohnesorge number for water at room temperature is approximately 0.004, which is significantly less than 0.01, indicating that its influence on jet breakup is negligible

3.2. High Speed Imaging and Processing

The breakup of the liquid jet is primarily governed by aerodynamic forces, which induce surface instabilities that grow in amplitude and eventually lead to disintegration into ligaments and droplets. As a result, the penetration height, penetration length, and breakup location vary with time, even under the same momentum flux ratio. High-speed images were acquired at 3000 fps with an exposure time of 40 µs, capturing 3000 frames over one second. Each frame was processed using MATLAB, and an ensemble average over all images was used to determine mean penetration height, length, and breakup location. Here, the breakup location is defined as the point along the jet axis where the continuous liquid column transitions into ligaments and droplets, while the penetration height refers to the maximum transverse displacement of the jet prior to breakup. Image processing involved background subtraction to remove noise, followed by cropping to a consistent 240 × 240-pixel region to isolate the spray zone. These preprocessed images were then used for Proper Orthogonal Decomposition (POD) to extract dominant coherent structures associated with the primary breakup dynamics. Spray visualization was performed using a 4-megapixel Phantom V341 high-speed camera.

3.3. Proper orthogonal decomposition

The Proper Orthogonal Decomposition is a well-established mathematical technique widely used to identify coherent structures embedded within a flow. The snapshot-based approach to POD involves collecting an ensemble of snapshots from either experimental measurements or numerical simulations and using them to generate a set of basic functions that span the dataset. In this analysis, intensity snapshots of the spray are utilized. The first step is to compute the mean spray image, which represents the zeroth mode of POD. The subsequent analysis focuses on the fluctuating component of the spray intensity relative to this mean image.

Each snapshot is essentially a 2D matrix, where each cell corresponds to the intensity value of a specific pixel in the spray image. For a snapshot of m × n pixels, there are a total of mn intensity values. These intensity values, obtained from N snapshots, are then arranged into a matrix U, which serves as the input for the POD analysis.

(1)

(2)

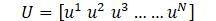
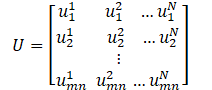
The auto-covarince matrix is then created as

(3)

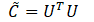
And the corresponding eigenvalue problem

(4)

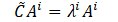
is solved. For convenience, the eigenvectors are ordered according to the magnitude of the eigenvectors

(5)

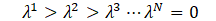
For convenience, the eigenvectors are normalized. The eigenvectors of (3) make up a

basis for the construction of POD modes ϕ^´,

(6)

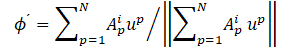
where A_p is the p^th component of the eigenvector corresponding to from (3) and the discrete 2-norm is defined as

(7)

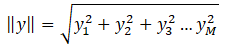
The eigenvectors are orthogonal and the eigenvalues are real and non-negative because of the self-adjoint and non-negative properties of the auto-covariance matrix.

Each snapshot can be expressed as a series of the POD modes with coefficients a; for each POD mode i. These POD coefficients are determined by projecting the fluctuating part of the spray onto the POD modes

(8)

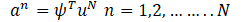
Where  has been introduced. The expansion of the fluctuating part of a snapshot n is

(9)

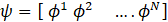
Fukunga showed that the total energy from the fluctuations in the snapshot that is associated with a given POD mode is proportional to the corresponding eigenvalue. Therefor the ordering of the eigenvalue and eigen value that the most important modes in terms of energy contribution are the first modes. This usually means that the first modes will be associated with large scale structure. If a flow has dominant flow structures. These are reflected in the first pod modes. Hence a given snapshot can often be reconstructed satisfactorily using only the few modes. The POD analysis presented in this study was performed using a dataset comprising 1000 image frames (N = 1000), each with spatial dimensions of 240 × 240 pixels (m = 240, n = 240).

4. Results and discussion

The high-speed image sequence illustrates the temporal evolution of a liquid jet injected perpendicularly into a crossflowing air stream, captured at 3000 frames per second. The flow condition corresponds to a liquid-to-air momentum flux ratio of 10 and a Weber number of 28, representing a regime where aerodynamic forces moderately dominate over surface tension. As shown in Figure 3, the high-speed image sequence captures the primary breakup of the liquid jet in crossflow. The jet undergoes significant deflection, surface wave development, and ligament formation, which subsequently leads to droplet pinch-off—indicating a transitional breakup regime between bag and multimode modes. Under such conditions, the jet undergoes significant deflection and distortion due to the high momentum of the crossflowing gas relative to the liquid phase. In the early frames (1–2 ms), the liquid jet is seen to bend downstream immediately upon exiting the injector, a characteristic behavior in low momentum flux ratio scenarios. The air stream exerts a strong shear force on the windward side of the jet, initiating Kelvin–Helmholtz (KH) instabilities along the shear layer. These instabilities manifest as small surface ripples and wave-like undulations that grow over time. Wu et al. [29] extensively studied such interactions and identified the development of KH instabilities as the dominant mechanism for the onset of breakup in subsonic crossflows at moderate Weber numbers [29].

As time progresses (20–22 ms), the instabilities grow into larger amplitude waves, and ligaments begin to form at the crests, particularly along the lateral edges of the jet. This marks the transition into a regime where surface tension and aerodynamic stretching begin to interact. The liquid column becomes elongated and thinned, eventually generating long ligaments that indicate the early stages of droplet formation. Mashayek et al. [30] similarly observed the formation of such structures and attributed them to a competition between aerodynamic stripping and capillary wave breakup, especially in the transitional Weber number regime [30].

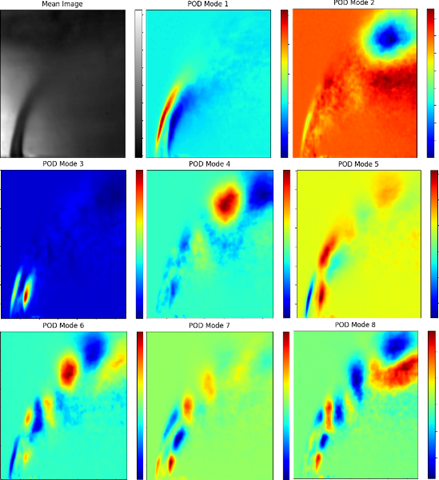
In the final set of frames (56–57 ms), the breakup process appears fully developed, with long ligaments clearly visible and in the process of pinching off into large primary droplets. The absence of fine mist and the presence of coherent, stretching ligaments suggest that the breakup is not in the shear-dominated regime. Instead, it aligns with what is commonly referred to as multimode breakup—a mixture of bag-type deformation followed by ligament stretching and capillary fragmentation. This behavior is consistent with the experimental observations of Sallam and Faeth [31], who documented that for Weber numbers between 20 and 50, breakup occurs via surface wave growth, ligament extension, and subsequent droplet shedding [31]. The Proper Orthogonal Decomposition is a powerful technique for identifying coherent structures in turbulent flows, with each POD mode representing a dominant spatial structure that contributes varying levels of energy to the overall flow dynamics. Figure 4 presents the first eight POD modes for q=15, at atmospheric pressure in a jet-crossflow configuration. The first mode captures the largest-scale coherent structures in the jet, primarily governed by shear layer instability at the interface with the crossflow. Large vortex rings and shear layer roll-ups are evident, alongside core jet penetration and crossflow interaction, with high-energy structures suggesting Kelvin-Helmholtz (KH) instability. As the modes progress, secondary instabilities begin to emerge. Mode 2 reveals flow asymmetries and secondary instabilities in the shear layer roll-up, with slight tilting of structures indicating the presence of counter-rotating vortices and the onset of smaller-scale instabilities. Mode 3 captures the interaction between large vortices and the jet core, where vortex stretching becomes prominent and the jet column starts to fragment into smaller vortical structures. The KH instability evolves into a more chaotic turbulent state, enhancing mixing through vortex pairing. By Mode 4, the jet column undergoes noticeable deformation, with coherent vortex cores breaking into filaments and instabilities migrating toward the wake region, indicating interactions with the downstream crossflow wake. The transition to turbulence becomes more evident in Mode 5, which represents the breakdown of the shear layer and the onset of turbulence transition Large-scale structures from previous modes disintegrate into finer vortices, and the shear layer loses coherence, marking the progressive onset of turbulence, with spanwise vortex stretching becoming visible. In mode 6, secondary and tertiary instabilities dominate, leading to further fragmentation of structures and clear evidence of vortex tilting and rotation. This mode signifies the transfer of energy from large coherent vortices to smaller turbulent structures, reflecting the classic energy cascade in turbulent flows. Mode 7 highlights wake instabilities, where the wake region behind the jet becomes dominant, characterized by Von Kármán-like vortices and strong asymmetry in the downstream structures due to the interaction between the crossflow and jet remnants. Mode 8 captures fully developed turbulence, where the flow field becomes highly disordered, with the energy cascade fully active and dominated by fine-scale turbulent eddies, representing turbulent dissipation structures.

As the mode number increases, the energy contribution decreases, transitioning from large-scale coherent structures in the initial modes to fine-scale turbulent fluctuations in higher modes. This progression highlights the energy cascade mechanism and the development of turbulence in the jet-crossflow interaction, where large vortices break down into smaller eddies, leading to a fully developed turbulent state further downstream. Figure 5 illustrates the percentage of energy contribution across different POD modes. Figure focuses on the first 50 modes to provide a clearer understanding of their contribution. The energy contribution declines rapidly as the mode number increases, highlighting that only a limited number of modes are responsible for capturing the dominant flow structures. Mode 1 exhibits the highest energy contribution, representing the most dominant coherent structure, which is likely the large-scale vortex system in the jet shear layer

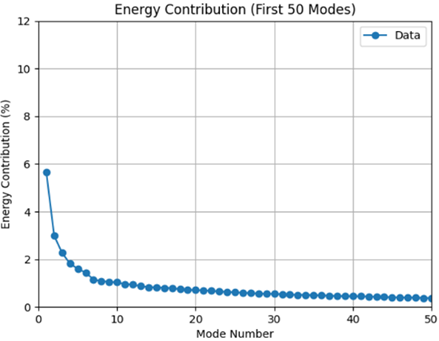
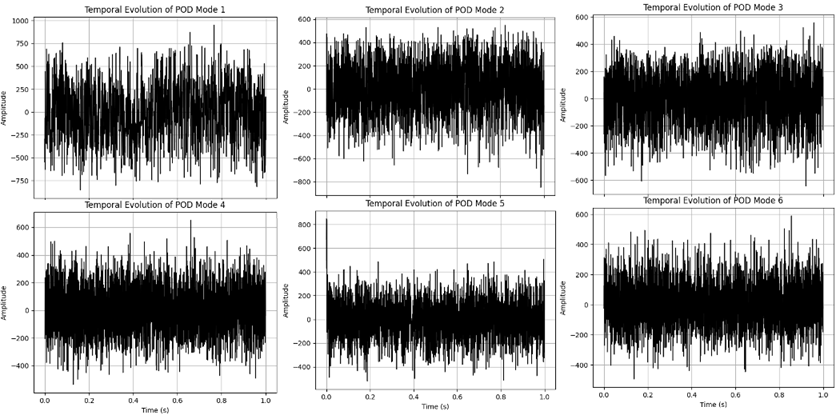
Modes 2–5 still retain a significant portion of the energy, corresponding to secondary instabilities such as vortex pairing, stretching, and jet-core interactions.  However, beyond Mode 10, the energy contribution becomes minimal, indicating that only the first few modes contain physically meaningful flow structures, while the higher modes predominantly represent fine-scale turbulence. As the mode number increases further, approximately beyond 50–100 modes, the energy levels out, implying that modes in the range of 100 to 3000 primarily account for noise and small-scale turbulent fluctuations.  The majority of the energy is captured within the first 10–50 modes, suggesting that low-order reconstructions of the jet flow using only these modes can still effectively capture the key coherent structures without requiring the full 3000-mode spectrum. The dominance of the first few modes in the energy spectrum confirms that the jet in crossflow contains strong coherent structures in its initial evolution. While higher-order modes (above 50–100) contribute very little energy, they remain essential for accurately resolving turbulent dissipation and chaotic fluctuations. If the flow reconstruction is limited to only a few dominant modes, the large-scale vortices will be retained, but finer turbulence details will be lost. Therefore, while a small number of modes are sufficient to represent the primary flow features, capturing the full turbulence spectrum requires incorporating higher-order modes to resolve the fine-scale structures and turbulent dissipation mechanisms. Figure 6 presents the temporal coefficients for the first six POD modes at q=15 under atmospheric conditions, illustrating how each mode’s contribution fluctuates over time. These time-series signals provide insight into the dynamic behaviour of coherent structures in the jet-crossflow interaction. Higher amplitude values indicate a stronger influence of a particular mode at specific times, revealing the evolution of turbulence and energy distribution across different scales. POD Mode 1 exhibits the highest amplitude range (~ ±750 to ±1000), capturing the most dominant, low-frequency coherent structures.  This mode primarily represents large-scale vortex structures in the shear layer, characterized by slow, strong oscillations. POD Mode 2 has a lower amplitude (~ ±400 to ±600) than Mode 1, but begins to capture shear layer instabilities, leading to the development of secondary vortical structures. The oscillations in this mode appear at a higher frequency, indicating the onset of more dynamic fluctuations compared to Mode 1. POD Mode 3, with an amplitude similar to Mode 2 (~ ±400 to ±600), represents weaker but still significant coherent structures, likely associated with vortex pairing and flow interactions. The presence of higher frequency content suggests increased flow unsteadiness, highlighting the transition to smaller-scale turbulence. POD Mode 4 exhibits a further decrease in amplitude (~ ±300 to ±500), indicating the presence of weaker vortices and turbulence transition features. The fluctuations become more random, marking the progressive breakdown of coherent structures into turbulent eddies. As the mode number increases, POD Mode 5 shows a further reduction in amplitude (~ ±200 to ±400), representing the onset of smaller-scale turbulence. The flow structures become more fragmented and less periodic, signifying the energy cascade from larger coherent vortices to finer turbulence scales. POD Mode 6, with the lowest amplitude (~ ±100 to ±300), is dominated by small-scale turbulence and fine-scale eddies. The oscillations appear more chaotic and less periodic, confirming the presence of high-frequency turbulence effects. The trends observed in the temporal coefficients align with the POD energy spectrum from the first 3000 modes. The first few modes (1–6) account for most of the total energy, and their decreasing amplitude reflects the energy distribution trend, where higher modes contribute progressively less energy. When linked to the spatial POD modes from the first 50 modes, these temporal coefficients describe the dynamic evolution of different flow structures. Modes 1–3 correspond to large-scale, coherent vortex structures, while Modes 4–6 transition toward smaller-scale turbulence.  Mode 1 dominates the global flow dynamics, exhibiting the largest and slowest oscillations, which represent the primary coherent structures governing jet-crossflow interaction. Higher modes, however, feature more chaotic and higher-frequency fluctuations, indicating the breakdown of large structures into finer turbulence scales. This follows the classical turbulence energy cascade, where energy is progressively transferred from large vortices to small-scale eddies, ultimately leading to a fully developed turbulent flow. The influence of the liquid-to-air momentum flux ratio on the primary breakup dynamics of a liquid jet in crossflow at a fixed Weber number of 28 is illustrated in the time-resolved image sequence. Figure 7 presents a time-resolved visualization of the primary breakup of a liquid jet injected into a crossflowing air stream with varying momentum flux ratios. The influence of the liquid-to-air momentum flux ratio on the primary breakup dynamics of a liquid jet in crossflow at a fixed Weber number of 28 is illustrated in the time-resolved image sequence. At the lowest value of q=4, the liquid jet is subjected to strong aerodynamic forces, resulting in immediate and significant deflection upon injection. The jet exhibits the formation of large-scale surface undulations driven by Kelvin–Helmholtz (KH) instabilities, leading to rapid disintegration via bag-like structures and ligament tearing. This behavior is characteristic of the bag or prompt breakup regime, where liquid inertia is insufficient to resist aerodynamic stripping, as described by Wu et al. [1] and further supported by the classification maps of Sallam and Faeth [6]. Similar characteristics under low momentum flux ratios were also reported by Kumar et al. [18] in an annular crossflow configuration.

As the momentum flux ratio increases to q=8, the jet displays moderate penetration while still governed by crossflow-induced instabilities. Surface waves grow into pronounced crests that evolve into ligaments, indicating a transitional breakup regime that combines features of both bag and multimode breakup. Such mixed-mode behavior—where surface instabilities and capillary-driven mechanisms interact—has been documented in both experimental and numerical studies [25,26]. At q=18, the jet core remains coherent over a longer axial distance due to increased liquid inertia. Breakup occurs primarily through column-mode mechanisms, with KH-induced ligaments forming at the periphery and detaching via capillary pinch-off. The transition from bag to column breakup with increasing q has been consistently observed across prior investigations [1,6,26].

At the highest momentum flux ratio in this study (q=24), the jet penetrates deeply into the crossflow, experiencing minimal deflection and delayed breakup. The breakup is dominated by the gradual formation of long, thin ligaments, which fragment due to surface tension effects. This behavior corresponds to the surface or column breakup regime, where higher jet momentum suppresses early instability growth and shifts the breakup region farther downstream. Similar observations were made in the works of Gopalan and Katz [27], Mazallon et al. [28], and Kumar et al. [18], highlighting the influence of increasing q on axial stability and downstream breakup location.

occurs at the jet periphery rather than through central bag rupture. At the highest tested momentum flux ratio, q=24, the liquid jet penetrates significantly into the crossflow, with only mild deflection observed.

The core remains largely intact over a greater downstream distance, and breakup is delayed. Ligaments formed at the jet edges are finer and longer,

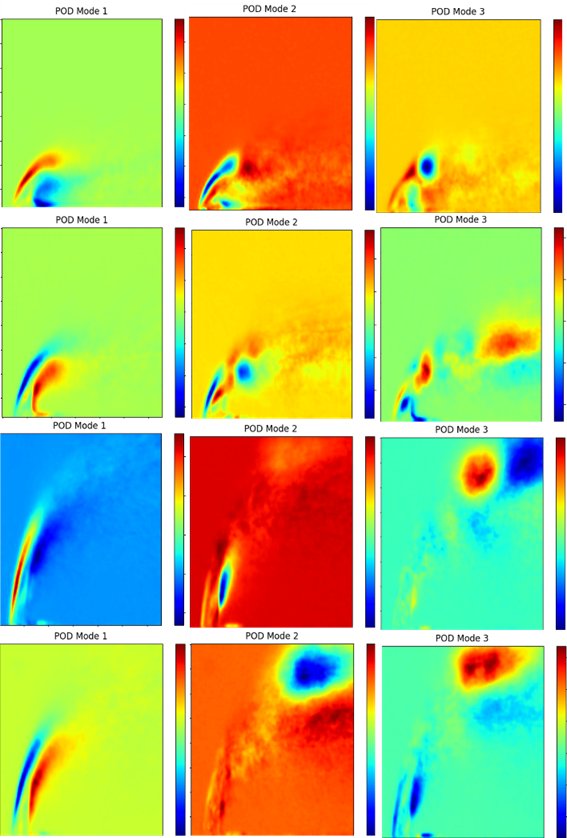
indicating a breakup mechanism dominated by surface wave growth under persistent shear forces. The observed evolution marks a transition into the surface breakup regime, where high liquid inertia suppresses early destabilization and promotes gradual disintegration through sustained aerodynamic interaction. These visual observations align well with established breakup maps and prior experimental findings for jets in crossflow at moderate Weber numbers. Figure 8 presents the first three proper orthogonal decomposition (POD) modes for a liquid jet in crossflow, analyzed at four momentum flux ratios (q=4,8,18,24), shown from left to right. The use of POD, originally formalized by Lumley [14] and later expanded by Berkooz et al. [21], allows the extraction of dominant coherent structures from complex, unsteady flow fields. In the current study, the first mode (Mode 1) captures the most energetic flow features, typically associated with large-scale vortical structures and jet core deflection. Mode 2 and Mode 3 reveal progressively smaller-scale motions, including vortex pairing, wake interactions, and transitional turbulence structures.

At low momentum flux ratio (q=4), the jet is highly susceptible to crossflow forces, exhibiting significant bending and early instability onset. Mode 1 shows a strongly deflected jet core and shear-layer roll-up, Mode 2 captures wake-driven instabilities, and Mode 3 reveals fine-scale structures indicative of rapid turbulence breakdown. This behavior aligns with findings in POD-based jet breakup studies where low momentum jets in crossflows exhibit dominant shear-induced instability modes and early loss of coherence [22,23]. As q increases to 8, the jet begins to exhibit stronger axial penetration and better structural organization. Mode 1 displays a more stable jet core, while Mode 2 highlights coherent vortex roll-up and pairing events. Mode 3 captures interactions in the wake region, suggesting delayed turbulence onset. This regime reflects a balance between jet inertia and crossflow shear, leading to the formation of large-scale Kelvin–Helmholtz vortices—a pattern also observed in POD analyses of impinging and wall-jet configurations [24]. At higher momentum flux (q=18), the jet largely resists bending and maintains coherence over a longer downstream distance. The POD modes indicate persistent large-scale vortical structures (Mode 1), vortex stretching and modulation (Mode 2), and the emergence of smaller scales farther downstream (Mode 3). Such delayed transition and long-lived coherent structures have been documented in modal studies of atomizing jets under elevated jet-to-air momentum conditions [4]. At q=24, the jet transitions to a fully jet-dominated regime with minimal influence from the crossflow. Mode 1 reveals strong penetration and core coherence, Mode 2 is characterized by internal shear-layer breakdown, and Mode 3 displays fine-scale turbulence that appears to be self-induced rather than externally triggered. This high-momentum regime is representative of free-jet behavior, where turbulence evolves internally within the jet shear layer—a phenomenon well captured in POD-based characterizations of free and axisymmetric jets [14,22].

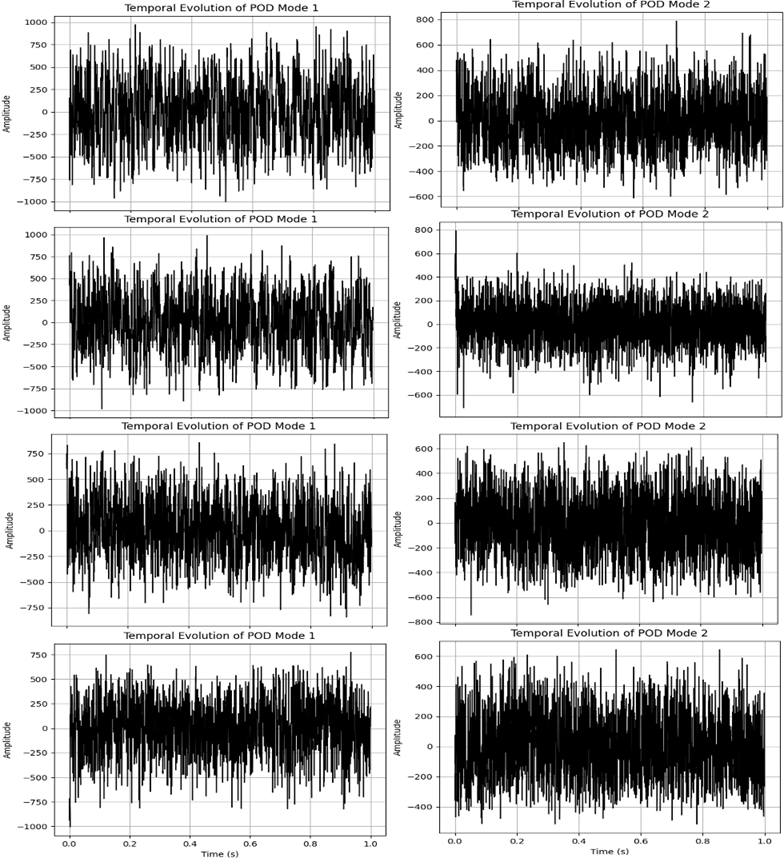
The temporal behavior of the dominant modes, shown in Figure 9, further emphasizes this transition in flow dynamics. At low q, temporal coefficients for Mode 1 and Mode 2 exhibit high-frequency, low-amplitude fluctuations, indicating early and chaotic instability development. As q increases, these signals become more energetic and structured, reflecting coherent vortex evolution and delayed turbulence breakdown. At the highest momentum ratio, fluctuations are dominated by self-sustained shear-layer dynamics, with minimal crossflow interaction. This trend aligns with observations by Muralidhar et al. [23], who noted the suppression of wake-induced turbulence and the emergence of internally driven vortex breakdown in high- q regimes.

Overall, the POD analysis highlights a clear transition from crossflow-dominated turbulence at low momentum flux ratios to jet-dominated self-induced turbulence at higher values. This transition significantly alters the spatial organization and temporal dynamics of the flow, underscoring the critical role of momentum flux ratio in controlling jet–crossflow interactions.

5. Conclusion

This study uses Proper Orthogonal Decomposition to analyse the coherent structures, energy distribution, and temporal evolution of a jet in crossflow at different momentum flux ratios. The results reveal that the first few POD modes capture the dominant large-scale structures, while higher modes represent fine-scale turbulence and dissipation. At low 𝑞, the jet is strongly influenced by the crossflow, leading to early turbulence formation driven by shear-layer instabilities. As 𝑞 increases, vortex roll-up and coherent structures persist longer, delaying turbulence onset. At high 𝑞, the jet maintains its integrity over a longer distance, forming strong Kelvin-Helmholtz vortices, with turbulence transition occurring further downstream. At very high 𝑞, the jet behaves almost independently of the crossflow, with turbulence primarily driven by internal shear-layer instabilities rather than external interactions.

The energy spectrum confirms that a small number of modes effectively capture the primary flow structures, with the first 10 containing most of the energy. Temporal analysis further illustrates the evolution of coherent structures, showing a shift from crossflow-dominated turbulence at low q to self-sustained turbulence at high q.

 

Nomenclature

References