Volume 12 - Year 2025 - Pages 181-194
DOI: 10.11159/jffhmt.2025.020
CALPHAD-Based Analysis of Composition and Operating Conditions on INCONEL 800HT Stability in Power Applications
Hanna Purzyńska1, Roman Kuziak1, Adam Zieliński1, Łukasz Poloczek1
1Łukasiewicz Research Network – Upper Silesian Institute of Technology
ul. K. Miarki 12-14, 44-100 Gliwice, Poland
hanna.purzynska@git.lukasiewicz.gov.pl, roman.kuziak@git.lukasiewicz.gov.pl,
adam.zielinski@git.lukasiewicz.gov.pl, lukasz.poloczek@git.lukasiewicz.gov.pl,
Abstract - The study conducts numerical analyses to examine the effects of chemical composition and temperature on the thermodynamic stability of phases and the kinetics of precipitation processes in INCONEL 800HT alloy. The findings elucidate phase stability trends, precipitation mechanisms, and radiation-induced modifications, contributing to the optimization of alloy performance in high-temperature environments.
Keywords: INCONEL 800HT, CALPHAD method, Phase stability, Precipitation kinetics, Thermodynamic modelling, High-temperature alloys.
© Copyright 2025 Authors - This is an Open Access article published under the Creative Commons Attribution License terms Creative Commons Attribution License terms. Unrestricted use, distribution, and reproduction in any medium are permitted, provided the original work is properly cited.
Date Received: 2025-01-17
Date Revised: 2025-05-19
Date Accepted: 2025-05-30
Date Published: 2025-06-04
1. Introduction
The INCONEL 800HT alloy is extensively utilized in high-temperature industrial applications, including components for boilers, cracking furnace tubes in the petrochemical sector, and electrical heating element shields. [1], [2] A notable application of INCONEL 800HT is in the Very High Temperature Reactor (VHTR), a graphite-moderated, helium-cooled nuclear reactor with a thermal neutron spectrum. The VHTR operates with core outlet temperatures reaching approximately 1000°C, enabling efficient utilization of heat for hydrogen production and other energy-intensive industrial processes.[2], [3]
Preliminary calculations were performed using the available thermodynamic databases: TCFe11, SSOL4, and TCNI9. Based on the comparison of the calculation results using these databases with the results obtained in [2], the TCNI9 database, developed for nickel superalloy, was selected for further calculations. For the analyzed case, the decomposition products of the solid solution in the INCONEL 800HT alloy are the following phases: Ti(C,N) – carbonitride with variable carbon and nitrogen content, M23C6 carbide, sigma phase, high chromium BCC_B2 phase and Ni3Ti (phase γ').
The temperature intervals of thermodynamic stability and the volume fractions of the above phases strongly depend on the chemical composition of the alloy and the applied heat treatment. The calculations showed the following regularities:
- Carbone nitride Ti(N,C) is the most stable phase, formed in the liquid state. For this reason, Ti(N,C) particles grow to large sizes and do not make a large contribiution to precipitation hardening, as they cannot be dissolved at the applied solution treatment temperatures. The chemical composition of particles formed in the liquid state is similar to that of TiN, and as the temperature decreases, it approaches the chemical composition of TiC. Reduction of nitrogen contents in the alloy causes a decrease in the temperature of the beginning of Ti(C,N) formation and a decrease in the volume share of this phase in the alloy structure.
- M23C6 carbide is stable at temperatures below 900 °C. Cr and C cause an increase in the volume fraction of this phase; It affects the temperature of the onset of secretion to a lesser extent. The calculations showed that M23C6 carbide can be eliminated from the alloy structure by controlling the content of the Cr, Ni, C and N Kinetic calculations have shown that the maximum precipitation rate of M23C6 carbide within the grain boundaries is obtained at a temperature of about 820°C. During continuous cooling, the application of a cooling rate above 8°C/s inhibits the precipitation process of this carbide. The precipitation process of M23C6 under isothermal conditions includes the stages of nucleation and growth of embryos and coagulation. These processes occur at high speed at 875°C, which leads to large particle sizes – an average value of about 2 μm.
- The sigma phase is stable in a narrow temperature range, with a maximum fraction at around 690 °C. The volume fraction of the sigma phase strongly depends on the Cr and Ni contents. The maximum proportion is obtained when the Cr content is set at the upper level and the Ni content at the lower level of the content of these elements set in the standard for alloy 800HT. A high volumetric fraction of the sigma phase is also observed when the contents of Cr and Ni are set at their minimum levels. On the other hand, for the minimum Cr content and the maximum Ni content, the sigma phase is not present in the alloy structure. Kinetic calculations suggest that the formation and the growth of the sigma phase within the grain boundaries occurs much slower compared to the precipitation process of M23C6 carbide. The maximum rate of the process is achieved at a temperature of approximately 615°C. Under continuous cooling conditions, the formation of the sigma phase is inhibited for cooling rates above 0.02°C/s. The size of sigma phase particles after isothermal holding within its stability temperature range does not exceed 10 nm.
- An increase in titanium content, with a fixed nitrogen level, leads to an increase in the participation and increase in titanium content, with a fixed nitrogen level, leads to an expansion of the temperature range of stability for the Ni₃Ti phase. A similar effect is observed with an increase in aluminum content.
Crucially, this study extends beyond standard thermodynamic modeling by also considering the impact of radiation exposure, drawing on data from [5]. One of the most significant radiation-induced effects in the INCONEL 800HT alloy is a redistribution of Si and Cr at grain boundaries—an observation associated with radiation-induced segregation (RIS). This redistribution alters local chemistry and can significantly affect phase stability and transformation behavior, particularly for the sigma, M23C6, and Ni₃Ti phases. Simulation results also suggest the potential emergence of new phases, such as a Si-based G phase, under irradiation.
Importantly, this work represents one of the first attempts to model RIS effects in INCONEL 800HT using the CALPHAD method, offering a novel approach to integrating irradiation effects into thermodynamic predictions. By doing so, the study provides a more comprehensive understanding of phase stability under service conditions and supports the optimization of materials for advanced reactor environments. This integration of RIS modeling within a CALPHAD framework addresses a critical knowledge gap and significantly strengthens the case for the publication of this research.
2. Basics of Numerical Methods Applied in Model Studies
2. 1. CALPHAD Methods
One method for analyzing complex phase equilibrium systems and calculating thermodynamic state functions is the computer simulation of phase equilibrium systems. These calculations are conducted using the CALPHAD method [4] and [5]. This method is based on the mathematical representation of thermodynamic phase functions, with the Gibbs energy being the most significant. The simplest case involves chemical compounds with a fixed stoichiometry. The Gibbs free energy then depends on temperature, possibly pressure, and magnetic interactions [4]:

where C1 – C6 are material parameters.
Phase components of major technical alloys can exist over a wide range of chemical compositions, typically forming solid solutions. In this case, the Gibbs function must also account for the influence of the chemical composition of the solid solution on the internal energy. numerical calculations is formed by summing three components: The Gibbs energy for individual phases used in numerical calculations is formed by summing three components:
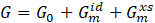
where G0 the reference state energy, ![]() is the ideal mixing energy, and is the excess mixing energy of the solid solution.
is the ideal mixing energy, and is the excess mixing energy of the solid solution.
The Gibbs energy of phases forming substitutional solid solutions can be described with sufficient accuracy using the following polynomial [4]:

where xi is the mole fraction of component i, ![]() is the Gibbs energy of component i in the reference state, T is the absolute temperature, R is the gas constant, and is the interaction parameter dependent on the value of v. If this value is 0, the alloy forms a regular solid solution; if it is between 0 and 1, a sub-regular solid solution f.orms The individual terms in equation (3) correspond to the Gibbs energy components defined by equation (2). The primary advantage of the discussed phase equilibrium modeling method is the ability to perform calculations for complex systems containing up to 20 components based on thermodynamic parameters determined for binary systems.
is the Gibbs energy of component i in the reference state, T is the absolute temperature, R is the gas constant, and is the interaction parameter dependent on the value of v. If this value is 0, the alloy forms a regular solid solution; if it is between 0 and 1, a sub-regular solid solution f.orms The individual terms in equation (3) correspond to the Gibbs energy components defined by equation (2). The primary advantage of the discussed phase equilibrium modeling method is the ability to perform calculations for complex systems containing up to 20 components based on thermodynamic parameters determined for binary systems.
Phase equilibrium system calculations involve searching for a set of phases and their chemical compositions in solid solutions for specified thermodynamic conditions where the Gibbs function reaches a minimum [6]:
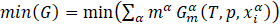
where: mα - phase fraction, ![]() - partial Gibbs energy of phase,
- partial Gibbs energy of phase, ![]() - concentration of component in phase. Parameters mα and
- concentration of component in phase. Parameters mα and ![]() are unknown, and their values are calculated by finding the minimum of the Gibbs function. The Newton-Raphson iterative method is used in the ThermoCalc program for this purpose [6].
are unknown, and their values are calculated by finding the minimum of the Gibbs function. The Newton-Raphson iterative method is used in the ThermoCalc program for this purpose [6].
Thermodynamic calculations presented in this report were conducted using the ThermoCalc program (v. 2023a). The program's key modules are thermodynamic databases and the POLY-3 module, which performs phase equilibrium calculations using numerical methods. The GES (Gibbs Energy System) module is used to develop thermodynamic models, while the Parrot module is used to optimize thermodynamic parameters based on measurement results obtained after heat treatment of metals and alloys, including volume fraction and chemical composition of phases in the structure. The data tabulation module allows for printing thermodynamic parameters and values in tabular form, while the Post Processor allows for creating graphical representations of calculation results. The accuracy of thermodynamic calculations depends primarily on the accuracy of the thermodynamic databases.
2. 2. Kinetic Calculations Using the TC-PRISMA Program
The TC-PRISMA program uses a numerical calculation method developed by Kampmann and Wagner, based on the Langer-Schwartz theory [7] and [8]. Classical Nucleation Theory (CNT) was used to model the nucleation process. According to this theory, the nucleation rate as a function of time is described by the following equation:

where: t - time, Js - steady-state nucleation rate τ - incubation period for nucleation.
The incubation period for nucleation is represented by the following formula:
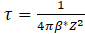
where: Z – Zeldovich factor, β – rate at which atoms attach to the nucleus, while Js is described by the following equation:
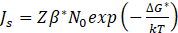
where: Z – Zeldovich factor, N0 – number of privileged nucleation sites per unit volume, ΔG* – Gibbs energy of forming a critical-sized nucleus, k – Boltzmann constant, T – absolute temperature.
ΔG* and β* are described by the following equations:
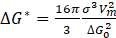
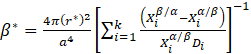
where: σ – interface energy particle/system, a – lattice constant, ΔG0 – driving force of the precipitation process, Xiβ/α and Xiα/β – molar fractions of component i at the interface and in the precipitate, Di – diffusion coefficient of component i in the system, Vm – molar volume of the precipitate, r is the critical radius of the nucleus, described by the following equation:
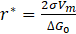
The Zeldovich factor is calculated using the following equation:
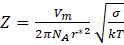
The most critical parameter affecting the kinetics of the precipitation process is the driving force of the precipitation process – ΔG0.
The driving force of the precipitation process is described by the following equation:
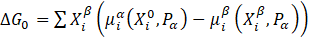
i = 1,2, ……, n
where: ![]() and
and ![]() - the chemical potential of element, i in the system and in the precipitate,
- the chemical potential of element, i in the system and in the precipitate, ![]() and
and ![]() is the molar fraction of element , i in the system and in the precipitate, and P^α is p is the pressure in the system.
is the molar fraction of element , i in the system and in the precipitate, and P^α is p is the pressure in the system.
The growth of the precipitate occurs after the formation of a nucleus of critical size. It is assumed that this growth is controlled/limited by the diffusion of elements in the system. Considering the condition of conservation of the diffusion flux of atoms, the growth rate of the precipitate is described by the following equation:
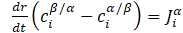 , i= 1, 2,…..,n
, i= 1, 2,…..,nwhere: ![]() -
- ![]() the concentration of element at the interface and in the system,
the concentration of element at the interface and in the system, ![]() - the diffusion flux of atoms of component and in the matrix a .
- the diffusion flux of atoms of component and in the matrix a .
The value of the atomic flux ![]() is calculated using Fick’s first law:
is calculated using Fick’s first law:
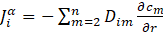
where: ![]() - – concentration gradient of atom m in the system around the precipitate, Dim – interdiffusion coefficient of atom i with reference to atom m.
- – concentration gradient of atom m in the system around the precipitate, Dim – interdiffusion coefficient of atom i with reference to atom m.
For the steady state ΔCi =0 and the combination of equations (13) and (14) leads to the equation:
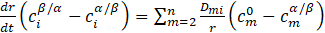
where ![]() – concentration of element m in the system far from the precipitate.
– concentration of element m in the system far from the precipitate.
The diffusivity of elements is a parameter dependent on the chemical composition of the studied system. To facilitate calculations in the TC-PRISMA program, diffusion coefficients are replaced by mobility coefficients found in the ThermoCalc databases and chemical potentials. After transformations, equation (15) takes the following form:
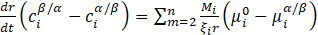
where ![]() – chemical potential of element i at the system/precipitate interface,
– chemical potential of element i at the system/precipitate interface, ![]() – chemical potential of element i in the system far from the precipitate,
– chemical potential of element i in the system far from the precipitate,
ξi – factor determining the effective range of diffusion.
In the calculations conducted in the described studies, a simplified model of the precipitation process was used, assuming that the chemical potential at the interface is modified by considering Gibbs-Thompson. One of the most important parameters in simulations of precipitation processes is the interfacial energy particle/system. This parameter is calculated using the Baker model:
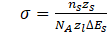
where ns– number of atoms per unit interfacial area, zs - number of cross bonds of atoms at the interface, zl– coordination number, NA – Avogadro's number, ΔEs – enthalpy of the solid solution.
3. Results of Numerical Calculations
The MS Word document must use Letter size pages with 2.54 cm top and bottom, and 1.2 cm left and right margins. A two column format is used with a width of 9.3 per column with a separation space of 0.59 cm. First lines of new paragraphs are indented by 1 cm. The body text is 11 pt Cambria, single-spaced, without 0 before and after paragraph spacing.
1. Equilibrium Calculations
The chemical composition of the 800HT alloy is presented in Table 1.
Table 1. Chemical composition of 800HT alloy (wt%).
|
Al |
C |
Cr |
Cu |
Fe |
|
0.51 |
0.076 |
20.82 |
0.046 |
45.17 |
|
Mn |
Ni |
S |
Si |
Ti |
|
1.09 |
31.49 |
0.002 |
0.015 |
0.49 |
|
H |
N |
O |
|
|
|
2.0 ± 0.4 [ppm] |
0.050; 0.055; 0.030 |
0.030; 0.020; 0.003 |
||
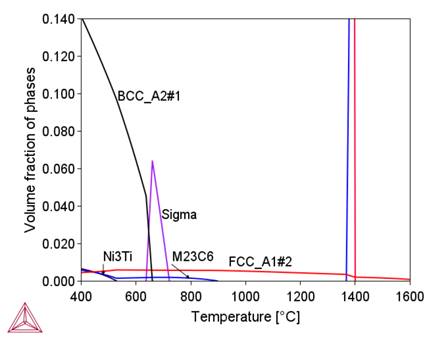
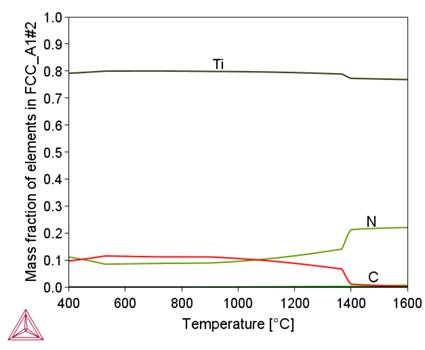
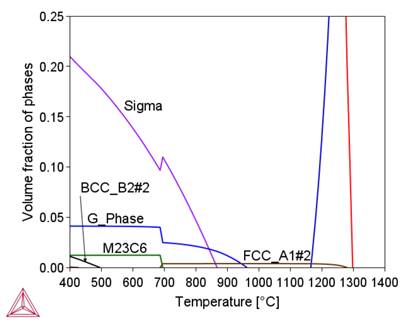
Preliminary calculations were performed using the available thermodynamic databases: TCFe11, SSOL4, and TCNI9. Based on the comparison of the calculation results using these databases with the results obtained in [3], the TCNI9 database, developed for nickel superalloy, was selected for further calculations. The changes in the proportion of phases in the thermodynamic equilibrium state as a function of temperature for the chemical composition of 800HT aloy calculated with the use of the ThermoCalc program are shown in Figure.1. Table 2 presents the characteristics of these phases. Changes in the chemical composition of phases – austenite decay products – are shown in
Figure 2.
Table 2. Characteristics of Phase Components in Alloy 800HT.
|
Component |
Cristal Structure Type |
Chemical Composition |
T1 [°C] |
T2 [°C] |
|
Liquid Phase |
- |
- |
1365 |
1402 |
|
Ti(C,N) |
FCC |
Ti, N, C |
- |
1669 |
|
M23C6 |
FCC |
Cr, Fe, C, Ni |
- |
896 |
|
Sigma |
Tetragonal |
Cr, Fe, Ni |
634 |
721 |
|
BCC_B2#2 |
BCC |
Cr, Fe, Ni |
- |
658 |
|
Ni3Ti |
Phase Hexagonal |
Ni, Ti |
- |
511 |

(a)
(b)
(a)
(b)
(c)
(d)
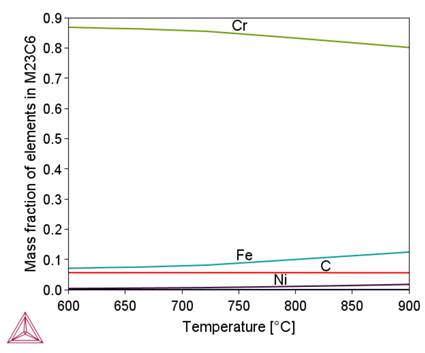
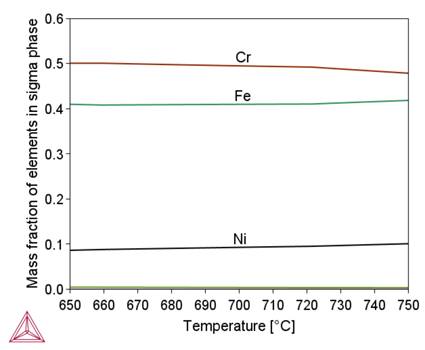
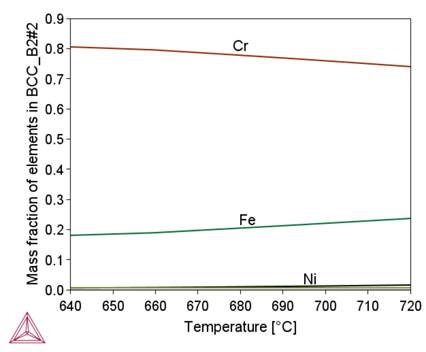
(c) Sigma; (d) BCC_B2#1.
Figure 2 shows that in the initial stage of separation from the liquid metal, the chemical composition of the complex carbide-nitride Ti(C,N) is similar to the chemical composition of the TiN nitride. As the temperature decreases, this composition approaches the chemical composition of TiC (increase in carbon content). As a result, an increase in the proportion of this phase in the alloy structure is observed (Fig. 1b). A similar effect of changing the chemical composition depending on the temperature is observed for M 23C6carbide, sigma phase and BCC_B2#1 phase. A common feature of these phases is the influence of their formation temperature on the chromium content, namely, as this temperature decreases, the chromium content in them increases. In the tested alloy, the Ni3Ti (γ') phase is stable below 510°C.
3. 2. Calculations of the Influence of Element Segregation Caused by Radiation on the Phase Composition of Alloy 800HT
Radiation-induced defects (RIS) diffuse into outlets, such as grain boundaries, and excess fluxes of defects cause non-equilibrium segregation of solute atoms due to the inverse Kirkendall effect [9] and [10]. The behavior of Cr and Ni atoms under the influence of radiation is well described, namely, it causes a decrease in the content of Cr and an increase in the content of Ni in the vicinity of grain boundaries. The RIS effect also increases the Si content. Local changes in the chemical composition cause a change in the equilibrium components of the alloy, which can cause a change in physical properties, such as corrosion resistance.
In the numerical tests carried out, the effect of radiation on the phase composition of alloy 800HT was also evaluated. For this purpose, the results of research published in the paper [10] were used. Measured changes in chemical composition in the vicinity of grain boundaries in this alloy, depending on the degree of radiation damage expressed by the dpa (displacement per atom) parameter, is given in Table 3.
Table 3. Changes in the chemical composition of the areas at the grain boundaries in the 800HT alloy under the influence of radiation [10].
|
|
800HT |
5 DPA |
10 DPA |
10 DPA’ |
|
Fe |
Rest |
Rest |
Rest |
Rest |
|
Cr |
20.42 |
17.42 |
15.42 |
14.42 |
|
Ni |
31.59 |
36.59 |
39.59 |
42.59 |
|
Al |
0.5 |
0.8 |
0.8 |
0.8 |
|
Mn |
0.76 |
0.26 |
0.26 |
0.26 |
|
Si |
0.13 |
2.53 |
4.53 |
4.53 |
|
Ti |
0.57 |
0.87 |
0.87 |
0.87 |
|
C |
0.069 |
0.069 |
0.069 |
0.069 |
|
Cu |
0.42 |
0.42 |
0.42 |
0.42 |
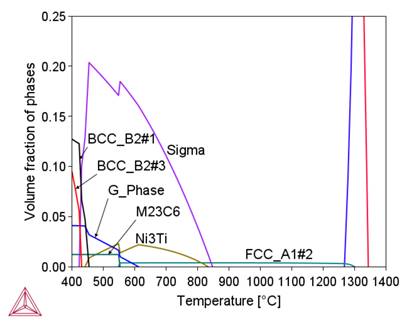
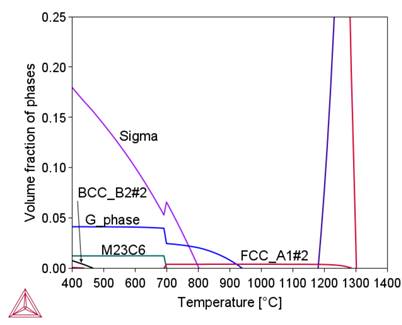
Table 3 shows that under radiation conditions the greatest concentration changes occur for Si, Cr, Ni, Ti and Mn. The effect of these changes on the phase composition is shown in Figure 3.
(a)
(b)
(c)
Figure 3 shows that segregation processes modify the phase composition of alloy 800HT locally. They primarily affect the content and temperature stability intervals of the sigma phase, M23C6 and Ni3Ti carbides. They also cause the formation of new phases, including the G-phase.
3.3. The kinetics of precipitation processes in 800HT
The kinetics of precipitation processes in 800HT were investigated using the TC-PRISMA program, associated with the ThermoCalc program. In contrast to equilibrium calculations performed with ThermoCalc, kinetic calculations take into account the local conditions under which the precipitation process occurs.
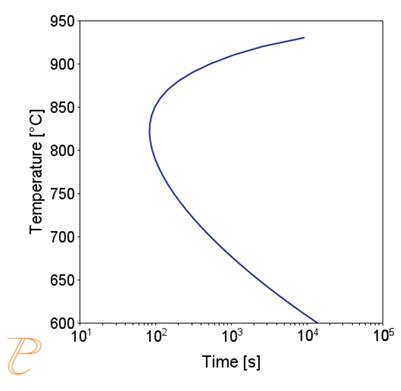
The precipitation process of M23C6 carbide was considered first. The privileged places of nucleation of this carbide are grain boundaries. Figure 4 (a) shows a calculated plot of CTP and precipitation process of M23C6 carbide along grain boundaries, assuming a grain size of 50 μm. The solution heat treatment temperature adopted in the calculations was 1000°C. The calculations show that the incubation period of the carbide precipitation process is the lowest at a temperature of about 830°C.
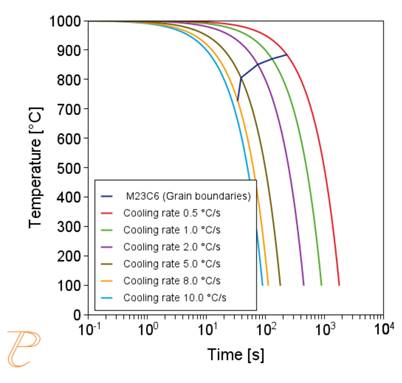
On the other hand, the CTPc diagram of the carbide precipitation process is shown in Figure 4(b). The calculations were performed for the cooling rate in the range of 0.5÷10°C/s, entering the same values of grain size and solution heat treatment temperature as in the CTPi plot calculations. As the calculations show, as the cooling rate increases, the temperature of the onset of carbide precipitation decreases, and for the cooling rate above 8°C/s, the precipitation process is inhibited.
Fig. 5 shows an example of the results of the simulation of the carbide precipitation process using a rate of 1°C/s.
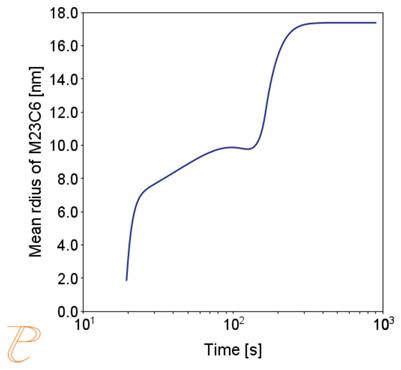
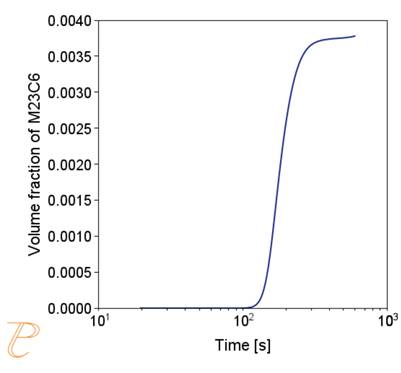
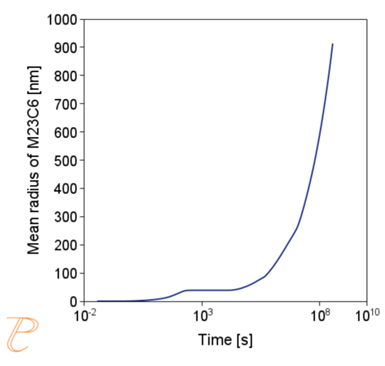
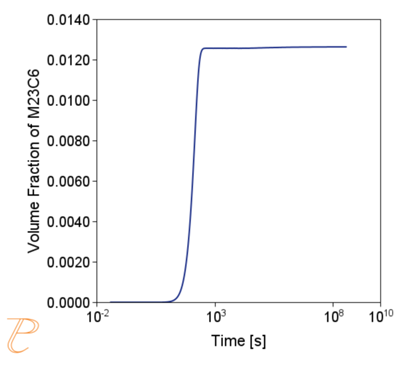
The simulations show that the precipitation process of M23C6 carbide under continuous cooling conditions is complex, namely, after the initial period of rapid growth of the average particle radius, growth slows down.
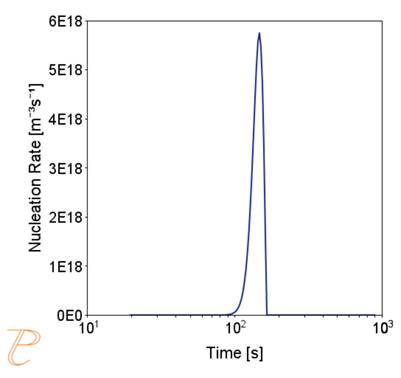
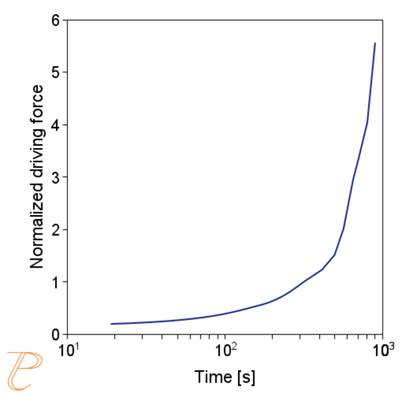
Figure 5(a)÷(e) shows that this is due to two factors. The first is an increase in the nucleation rate due to an increase in the driving force for the carbide precipitation process. The second factor – related to the first – is the systematic reduction of the critical radius of the embryo during the precipitation process.
(a)
(b)
(a)
(b)
(c)
(d)
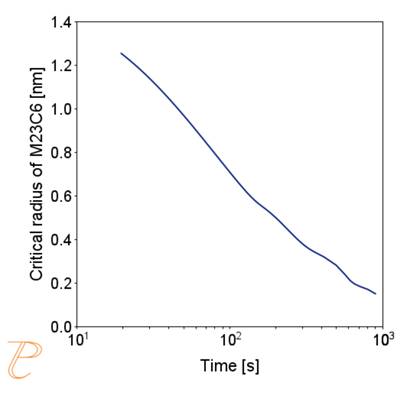
(e)
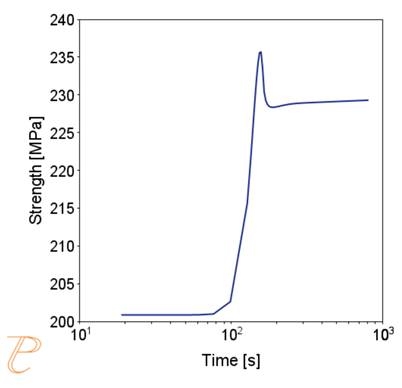
(f)
(e) critical radius; (f) contribution of precipitation hardening to yield strength.
The simulation results shown in Figure 6 and Figure 7 illustrate the progress of the carbide precipitation process at temperatures of 500 and 875 °C.
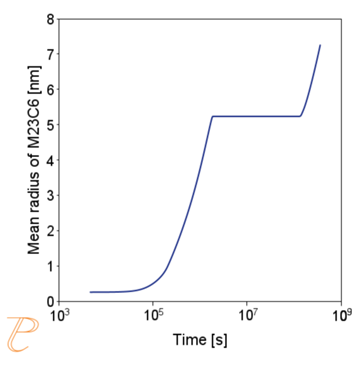
(a)
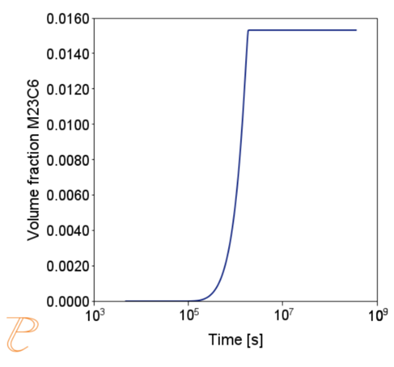
(b)
(a)
(b)
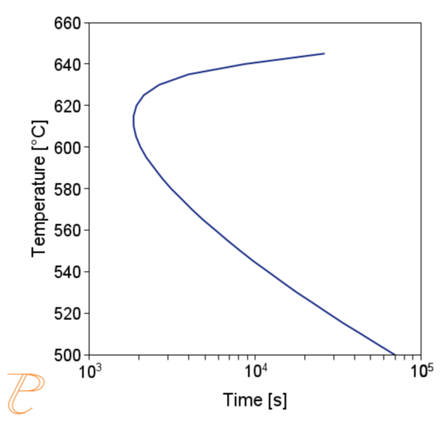
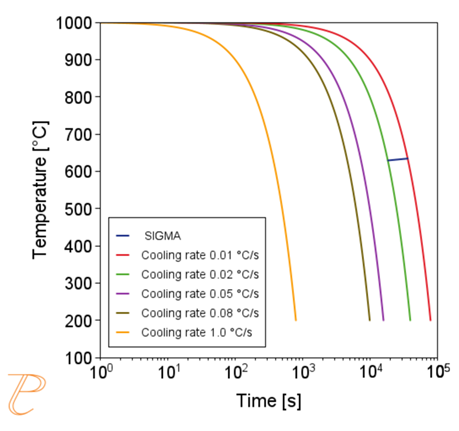
Subsequent simulations concerned the kinetics of the Sigma phase precipitation process. A graph of CTPi the precipitation process of the Sigma phase is shown in Figure 8. This figure shows that the precipitation process occurs much slower compared to the precipitation process of M23C6 carbide. For this reason, low walking speeds are required to initiate this process under conditions of continuous temperature changes (Figure 9) The calculations shown in Figure 9 show that the application of a cooling rate above 0.02°C/s inhibits the release of the Sigma phase. Another consequence of the kinetic characteristics of the Sigma phase precipitation process is the acquisition of small particle sizes of this phase even for long aging times (Figure 10 and 11).
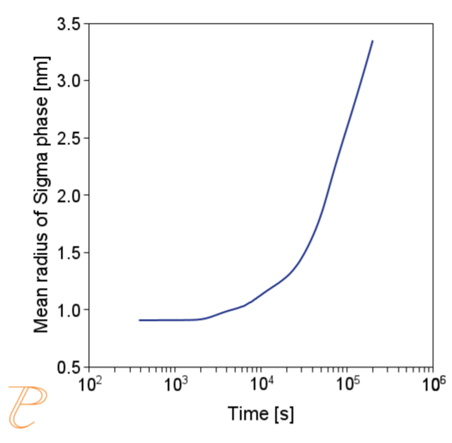
(a)
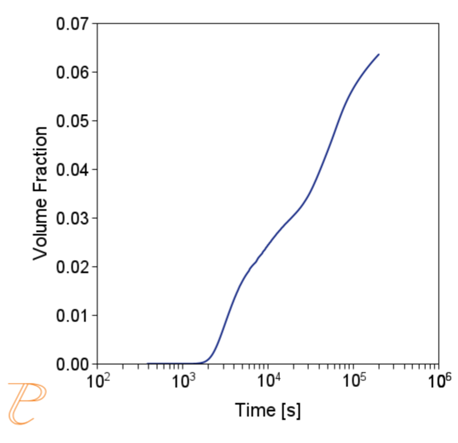
(b)
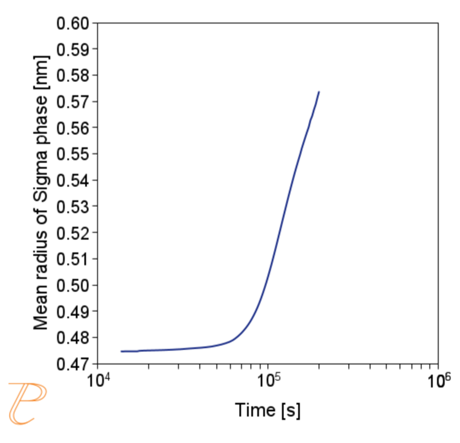
(a)
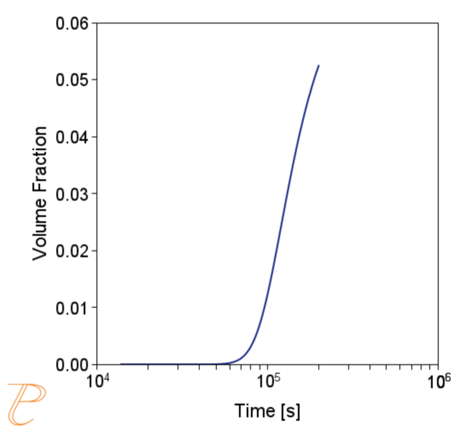
(b)
Conclusion
The temperature intervals of thermodynamic stability and the volume fractions of the above phases strongly depend on the chemical composition of the alloy and the applied heat treatment. The calculations showed the following regularities:
- Carbone nitride Ti(N,C) is the most stable phase, formed in the liquid state. For this reason, Ti(N,C) particles grow to large sizes and do not make a large contribiution to precipitation hardening, as they cannot be dissolved at the applied solution treatment temperatures. The chemical composition of particles formed in the liquid state is similar to that of TiN, and as the temperature decreases, it approaches the chemical composition of TiC. Reduction of nitrogen contents in the alloy causes a decrease in the temperature of the beginning of Ti(C,N) formation and a decrease in the volume share of this phase in the alloy structure.
- M23C6 carbide is stable at temperatures below 900 °C. Cr and C cause an increase in the volume fraction of this phase; It affects the temperature of the onset of secretion to a lesser extent.The calculations showed that M23C6 carbide can be eliminated from the alloy structure by controlling the content of the Cr, Ni, C and N Kinetic calculations have shown that the maximum precipitation rate of M23C6 carbide within the grain boundaries is obtained at a temperature of about 820°C. During continuous cooling, the application of a cooling rate above 8°C/s inhibits the precipitation process of this carbide. The precipitation process of M23C6 under isothermal conditions includes the stages of nucleation and growth of embryos and coagulation. These processes occur at high speed at 875°C, which leads to large particle sizes – an average value of about 2 μm.
- The sigma phase is stable in a narrow temperature range, with a maximum fraction at around 690 °C. The volume fraction of the sigma phase strongly depends on the Cr and Ni contents. The maximum proportion is obtained when the Cr content is set at the upper level and the Ni content at the lower level of the content of these elements set in the standard for alloy 800HT. A high volumetric fraction of the sigma phase is also observed when the contents of Cr and Ni are set at their minimum levels. On the other hand, for the minimum Cr content and the maximum Ni content, the sigma phase is not present in the alloy structure. Kinetic calculations suggest that the formation and the growth of the sigma phase within the grain boundaries occurs much slower compared to the precipitation process of M23C6 carbide. The maximum rate of the process is achieved at a temperature of approximately 615°C. Under continuous cooling conditions, the formation of the sigma phase is inhibited for cooling rates above 0.02°C/s. The size of sigma phase particles after isothermal holding within its stability temperature range does not exceed 10 nm.
- An increase in titanium content, with a fixed nitrogen level, leads to an increase in the participation and increase in titanium content, with a fixed nitrogen level, leads to an expansion of the temperature range of stability for the Ni₃Ti phase. A similar effect is observed with an increase in aluminum content.
The study also included an analysis of the impact of radiation on the phase composition of INCONEL 800HT alloy, based on the results presented in reference [5]. The most significant effect of radiation on the 800HT alloy is a substantial change in the content of Si and Cr at the grain boundaries compared to the chemical composition of the structure.
As a result, changes in the proportion and temperature stability ranges of the sigma phase, M23C6 carbide, and Ni3Ti phase can be expected. The computational results also indicate the potential formation of new phases, including the G phase, which is Si-based.
Although the presented study offers an extensive computational analysis of phase stability and precipitation kinetics, it is important to acknowledge certain limitations. The results are based primarily on numerical modeling without direct experimental verification. Assumptions such as idealized grain boundary behavior and homogeneity of diffusion conditions may not fully reflect real operational environments. Nevertheless, a portion of the experimental validation—covering metallographic and microanalytical studies of irradiated and heat-treated samples—has already been completed and will be published shortly. These findings will serve to confirm the key predictions of the CALPHAD and TC-PRISMA models and support further refinement of the simulation approach based on empirical data.
References
[1] H. Purzyńska, G. Golański; Incoloy 800HT iron-based superalloy – preliminary characterisation, Journal of Metallic Materials 2022, 74 (3-4), p. 42–46. DOI: 10.32730/imz.2657-747.22.3-4.5 View Article
[2] W. E. Pratt, Kinetic and thermodynamic modelling of long term phase stability in alloy 800H subject to LWR core conditions, Master Thesis, University of Tennessee, 2015. View Article
[3] W. Ren; R. Swindeman; Status of Alloy 800H in Considerations for the Gen IV Nuclear Energy Systems. J. Press. Vessel Technol. 2014, 136, 054001 View Article
[4] The SGTE Casebook Thermodynamics at Work, ed. K. Hack, The Institute of Materials, 1996. View Article
[5] M.Hillert, CALPHAD, vol. 4, 1980, 1. View Article
[6] H.L. Lukas, S.G. Fries, Bo Sundman; Computational Thermodynamics – The CALPHAD Method, Cambridge University Press, 2007. DOI: 10.1017/CBO9780511804137 View Article
[7] J. Langer, A. Schwartz; Phys. Rev. A 1980, 21, 948-958 View Article
[8] R. Wagner, R. Kampmann, Homogeneous second phase precipitation, in: P. Haasen ed., Mat. Sci. Techn.: Comprehensive treatment, Weinheim: Wiley-VCH,1991. View Article
[9] J.M. Titchmarsh, S. Dumbill; On the measurement of irradiation-induced segregation (RIS) at point defect sinks, Journal of Nuclear Materials, 227(1996) 203-219 View Article
[10] J.H. Shim; Modelling precipitation thermodynamics and kinetics in type 316 austenitic stainless steel with varying composition as initial step toward predicting phase stability during irradiation, Journal of Nuclear Materials, 462 (2015), 250-257. View Article

