Journal of Fluid Flow, Heat and Mass Transfer (JFFHMT)

ISSN: 2368-6111

Modeling Heat Transfer in Cylindrical Batteries: Spiral-Based Thermal Conductivity Tensor

Jiri Hvozda¹, Jan Bohacek¹, Alexander Vakhrushev², Ebrahim Karimi-Sibaki²

¹Heat Transfer and Fluid Flow Laboratory, Faculty of Mechanical Engineering
Brno University of Technology, Antoninska 548/1, 602 00 Brno, Czechia
Jiri.Hvozda@vut.cz; Jan.Bohacek@vut.cz
²Christian-Doppler Laboratory for Metallurgical Applications of Magnetohydrodynamics
Montanuniversitaet Leoben, Franz-Josef Strasse 18, 8700 Leoben, Austria
Alexander.vakhrushev@unileoben.ac.at; ebrahim.karimi-sibaki@unileoben.ac.at

Abstract - This study investigates the importance of considering the well-known spiral structure of cylindrical batteries in numerical models of heat transfer. Such models typically simplify the internal geometry by a concentric layout of electrodes and separators, resulting in an effective orthotropic thermal conductivity with radial, tangential, and axial components defined in a cylindrical coordinate system. However, the actual spiral structure suggests radius-dependent thermal conductivity. In this study, several thermal simulations were performed, comparing thermal fields obtained with the commonly used cylindrical orthotropy and a more realistic spiral structure. The results show that the spiral structure has a negligible effect on the overall temperature distribution for configurations with dense spirals and higher radial thermal conductivity (2 W·m⁻¹·K⁻¹). However, for lower radial thermal conductivity (0.2 W·m⁻¹·K⁻¹), considerable errors were observed even for dense spirals. These findings emphasize the need for studies to justify simplifications made in the thermal conductivity tensor.

Keywords: Battery thermal management systems, Li-Ion cylindrical batteries, orthotropic thermal conductivity, spiral structure.

© Copyright 2025 Authors - This is an Open Access article published under the Creative Commons Attribution License terms Creative Commons Attribution License terms. Unrestricted use, distribution, and reproduction in any medium are permitted, provided the original work is properly cited.

Date Received: 2024-11-18
Date Revised: 2025-01-20
Date Accepted: 2025-01-24
Date Published: 2025-01-30

1. Introduction

Maintaining optimal temperature within Li-Ion cylindrical batteries is crucial for performance and safety. The temperature should remain within the 15–35 °C range, with temperature variations across the battery pack kept below 5 °C to avoid uneven degradation. Effective thermal management is vital to achieving this, and numerical simulations have emerged as indispensable tools for exploring and developing these systems [1]-[3].

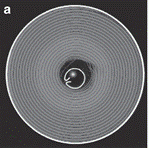
A critical aspect of battery design is the internal structure, where cylindrical cells feature a spiral-wound arrangement of electrodes and separators. This spiral structure, visible in CT scans of batteries obtained by Finegan et al. [4], see Figure 1, introduces complexities in heat transfer modeling. The most advanced thermal simulations incorporate the spiral's influence and electrochemical dynamics, such as concentration gradients and phase changes. While these high-fidelity models offer a detailed understanding of battery behavior, they are computationally intensive and energy-demanding, limiting their use to specific applications [5]-[7].

Simpler models are often employed for routine simulations, especially at low discharging or charging rates. These models assume constant heat generation rates and neglect the internal spiral structure [8], in some cases even simplifying the thermal conductivity as isotropic [9]. At higher rates, more complex models incorporate the reversible and irreversible heat generation components. However, they still neglect the cell spiral structure, i.e., employ thermal conductivity tensor components as constant [10]-[12].

Although numerous studies assume orthotropic thermal conductivity with constant values in cylindrical coordinates, they often omit a justification for disregarding the spiral structure. This simplification is likely due to the ease of implementation in standard CFD software, which typically employs cylindrical orthotropic material properties that seem to address the problem at first glance. However, this approach is not entirely accurate and requires careful consideration to ensure that important factors, such as the spiral structure, are not overlooked. This paper fills that research gap by presenting a series of numerical simulations that explicitly consider spiral geometry. Our results show that the spiral structure has a negligible impact on the overall thermal conductivity, thus validating the simplifications widely adopted in the literature.

2. Methods

2. 1. Governing equations and transformation from cylindrical to cartesian coordinates

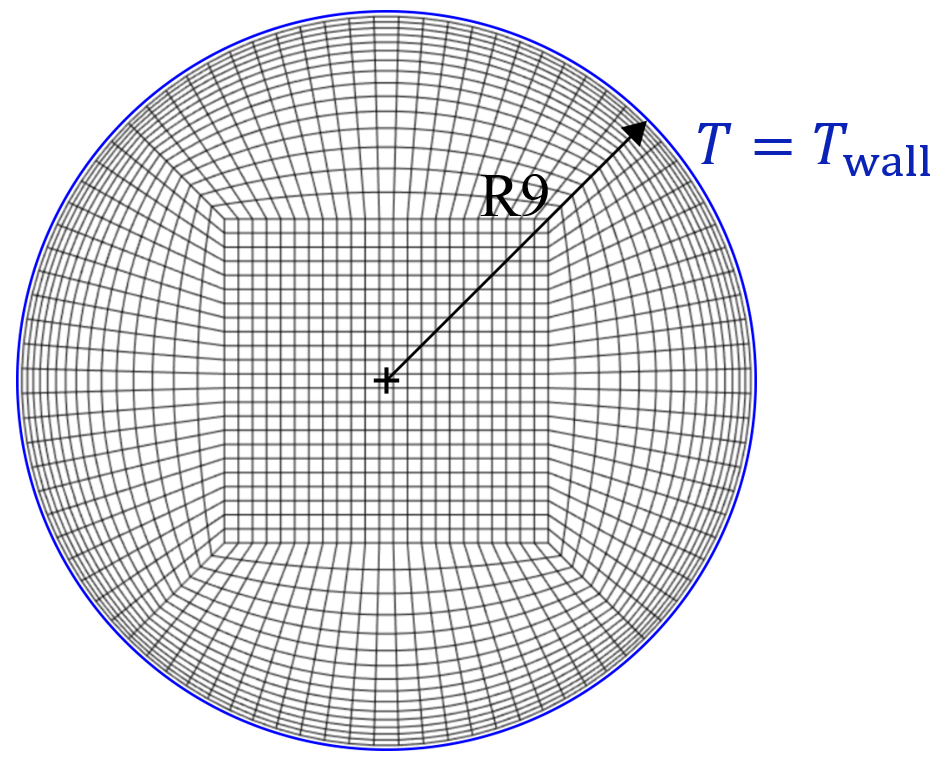
The computational domain consists of a cylinder with a radius of 9 mm (r_o) representing an 18650 Li-Ion cell, the cross-sectional slice with mesh is displayed in Figure 2. There are around 1800 elements in the slice; almost 85 % of the elements have a skewness lower than 0.10, and the average skewness is 0.06; the aspect ratio of the elements is not higher than 6.70, and the average value is 2.21. The case can be solved only in two-dimensional space x,y as heat transfer in the z-direction is trivial and is not connected with the primary goal of the present manuscript to test the influence of the spiral geometry on heat transfer. However, the equations and transformations are stated in three-dimensional space for their general usage. The Dirichlet boundary condition is set on the outer diameter of a cylinder with a constant wall temperature (T_wall) of 320 K. Steady state is assumed. This setting can simulate the case when a Li-Ion cell is discharging/charging at low current and immersed in a phase change material with a melting point of T_wall.

The heat transfer within the cylindrical battery was modeled using the steady-state heat conduction equation:

(1)

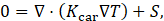
with Dirichlet boundary condition:

T=T_wall, for x,y so that x²+y²=0.009²,

(2)

where S represents the heat generation rate with a constant value of 100 kW·m⁻³. The thermal conductivity tensor K_car in the equation (1) must be implemented via transformation from local spiral (r,ϕ,z) to cartesian (x,y,z) coordinates:

(3)

(4)

(5)

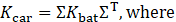
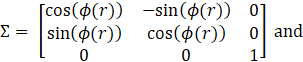
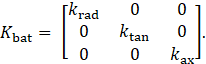
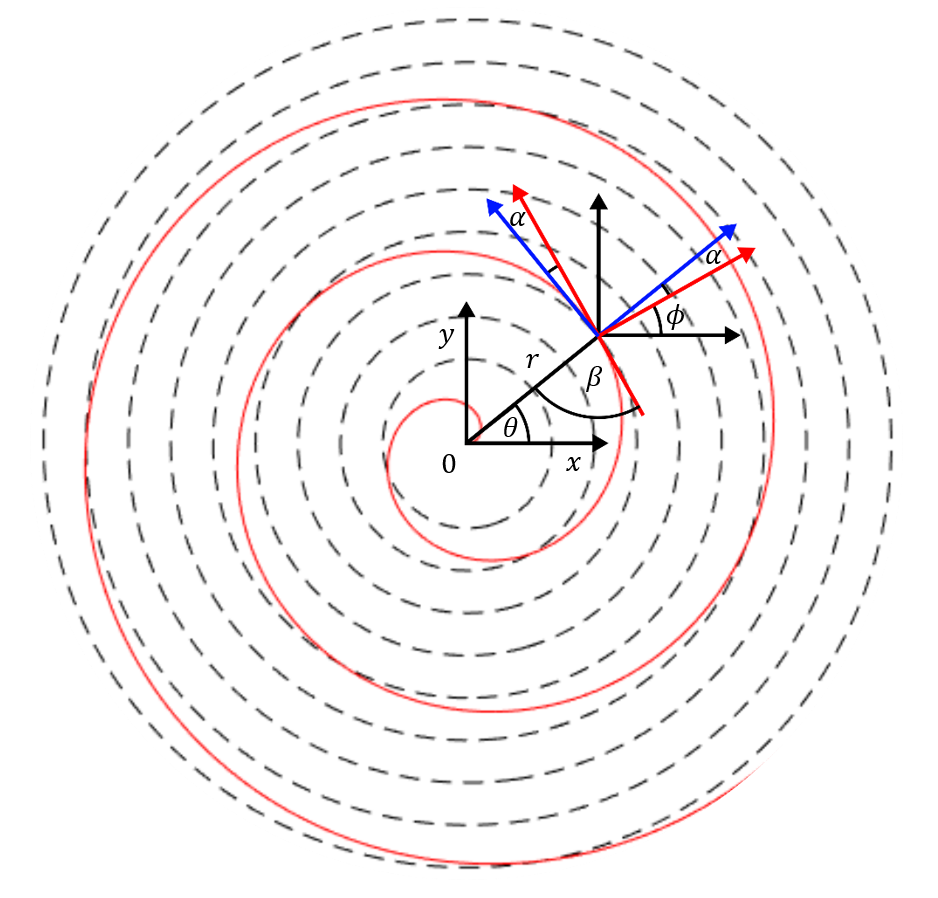
In literature, the thermal conductivity of a cylindrical battery is often simplified by assuming concentric cylindrical layers of internal components, thus defining the thermal conductivity tensor in cylindrical coordinates – radial (k_rad), tangential (k_tan), and axial (k_ax), particular values are given in Table 1. The spiral structure will not influence the latter; the others must be changed concerning the radius to reflect the deviation (α) between tangential vectors of the circle and spiral in their intersection. The derivation of angle ϕ(r) is illustrated in Figure 3 and is further described in the next section in detail.

Table 1: Thermal conductivity tensor components in the cylindrical coordinates of a cylindrical Li-Ion battery 18650 [13], [14].
Property	Value	Units
krad	0.2 or 2	W·m−1·K−1
ktan = kax	30	W·m−1·K−1

2. 2. Description of the radius-dependent thermal conductivity in cylindrical coordinates

Based on the previous figure, it is straightforward to see that we have to find the angle α for every feasible value of the radius, i.e., in the interval of 0 and 9 mm. Then, for any point (r,θ), the angle ϕ in eq. (3) is given as the difference of θ and α. Clearly, the sum of angles α and β is 90°. Let us proceed with finding the angle β. Note that, near the origin, the value β will be close to 0°, which is expected to increase and converge to 90° with increasing radius. In the following text, we will make the relations only in r,θ plane, as the spiral structure does not influence the behavior in z direction. The circle with radius R can be written as

(6)

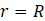
and the spiral follows as

(7)

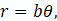
where b defines the gap between the spiral layers. The angle β can be obtained from the formula of the angle between a tangential of the spiral and radius vector as

(8)

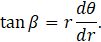
Further, derivation of equation (6) by θ and substituting term dθ/dr into (7) yields

(9)

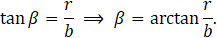
And, thus

(10)

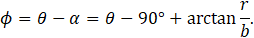
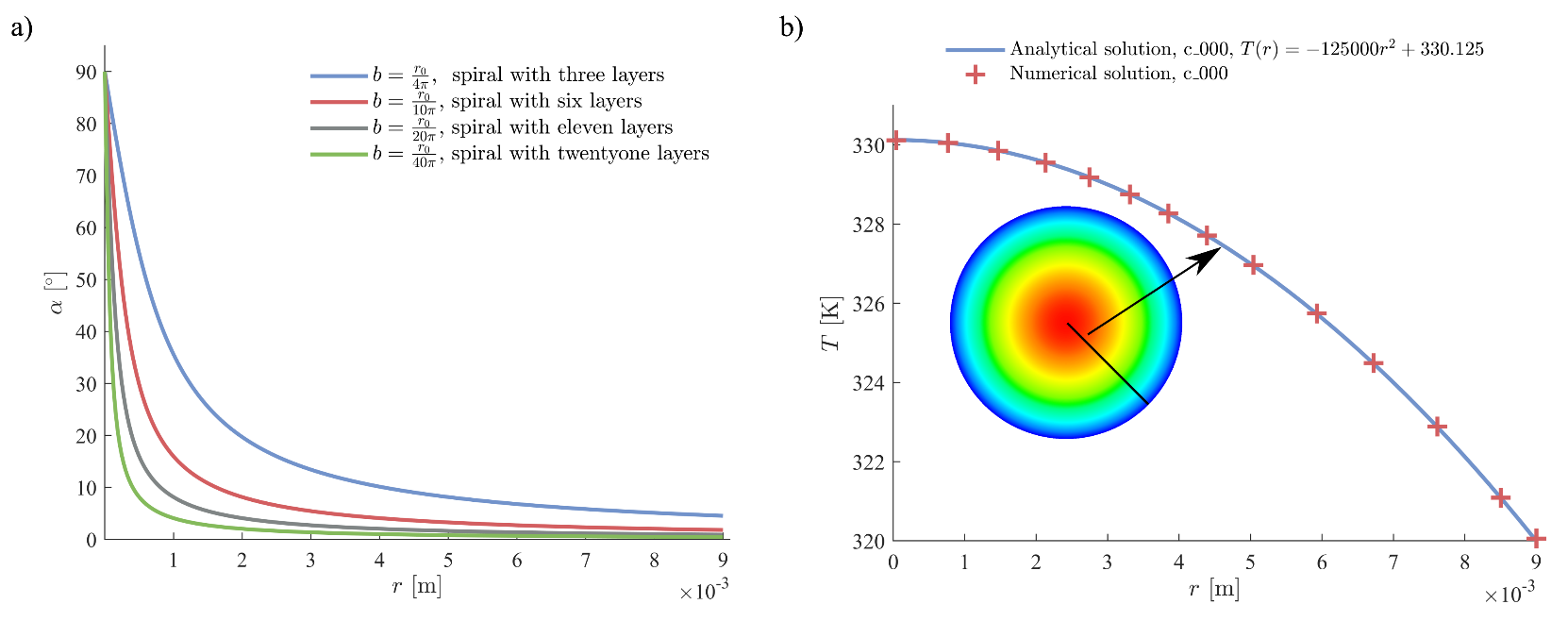
The resulting angle α is shown in Fig. 4 a), for four different b. In practice, actual values of b are somewhat lower than r₀/(20π) m, i.e., the spiral has more than eleven layers. For these cases, it can be seen that if the radius is higher than 1 mm, the angle α is lower than 8°. Hence, the difference between the constant and variable conductivity (based on the spiral structure) is minor, and no significant temperature difference is expected for cases with varying thermal conductivity with radius.

2. 3. Plan of the simulations

Simulations were performed in ANSYS Fluent 2024 R1. Several simulations were conducted for cases with constant thermal conductivities and varying conductivity concerning the radius described in the previous section for several setups of coefficient b. Their settings are shown in Table 2.

Table 2: Plan of the simulations.

case	b⋅2π/ro	krad	ktan
		[–]	W·m−1·K−1	W·m−1·K−1
c_000	–	0.2	30
s_020	20	0.2	30
s_010	10	0.2	30
s_005	5	0.2	30
s_002	2	0.2	30
c_100	–	2	30
s_120	20	2	30
s_110	10	2	30
s_105	5	2	30
s_102	2	2	30

3. Results

3. 1. Validation and verification

For the cases c_000 and c_100, i.e., one-dimensional heat conduction in steady state regime, equation (1) can be rewritten into the form

(11)

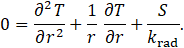
By standard approach, it can be analytically found the particular solution of temperature distribution along the radius inside the computational domain as

(12)

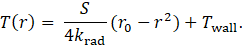
The comparison of analytical and numerical solutions of case c_000 are displayed in Fig 4 b). As can be seen, the numerical solution follows the correct analytical solution; thus, the numerical approach is assumed to be validated.

For cases that account for the influence of the internal spiral structure, it can be demonstrated that the tensor conductivity in eq. (4), with the angle ϕ defined by eq. (10), is implemented correctly. Consider the transient heat conduction equation in the form:

(13)

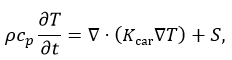
applied to the same domain (as shown in Fig. 2) of a circle with a radius of 9 mm. Here, S is zero everywhere except in the vicinity of the point [9⋅10^-3,0], where it is set to 10 MW⋅m^-3 within a radius of 0.5 ⋅ 10^-4m. All boundary conditions are adiabatic. Additionally, assume the radial thermal conductivity is zero while the tangential thermal conductivity is 30 W·m−1·K−1. Let us analyze the case for a one-turn spiral, i.e. b= r_0/(1⋅2π) ending in point [9⋅10^-3,0]. After the initialization and the first time-step of 0.001 seconds, a heat diffuse along the spiral can be observed (Fig. 5) as expected from the preceding description.

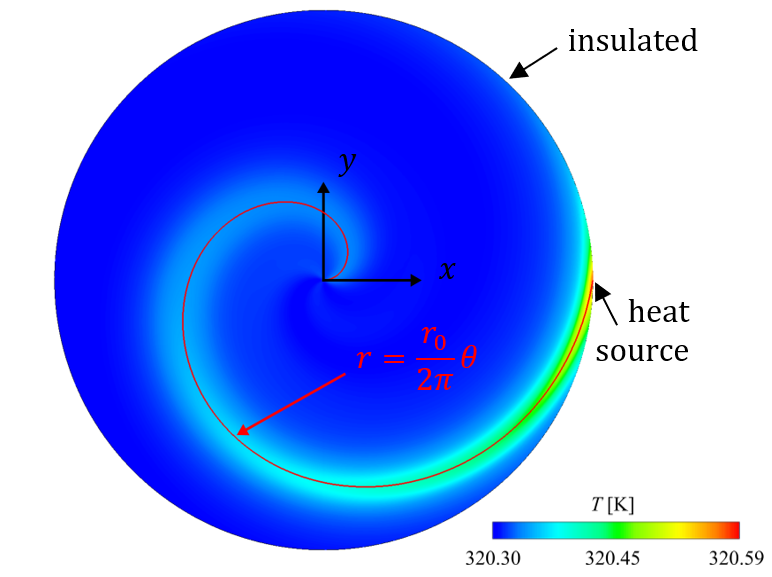
3. 2. Simulation outcomes

The simulation results for all cases are summarized in Table 3. Key parameters, i.e., the maximal temperature (T_max) and the maximal temperature spread (ΔT_max) within the computational domain, were recorded for each simulation. To evaluate the impact of spiral-based conductivity, the results from the spiral-based cases (s_020, s_010, s_005, and s_002) were compared against the benchmark case c_000. Similarly, cases corresponding to a higher radial thermal conductivity (s_120, s_110, s_105, and s_102) were analyzed, with c_100 as the reference benchmark. For each scenario, the comparisons included absolute differences (T_max,s-c) and relative errors (ε_max). Here, T_max,s-c represents the absolute deviation in maximal temperature between a spiral-based case and the respective benchmark, while  quantifies this deviation as a percentage relative to the benchmark value. Similarly, for the maximal temperature spread, absolute deviations (ΔT_max) and relative errors (ε_Δmax) were calculated. The term ΔT_max,s-c indicates the absolute difference in temperature spread between a spiral-based case and the benchmark, while ε_Δmax expresses this difference as a percentage of the benchmark value.

The results indicate that b significantly influences the maximum temperature inside the battery. The absolute error is up to 6.87 K, but the relative error is lower than 2.10 %. A significant difference can be observed for the maximal temperature spread, especially for very low values of b. The relative error goes up to almost 70 %. A low value of b causes high conductivity along the sparse spiral that effectively removes heat to the sides of the battery.

Table 3: Results of the simulations.
case	Tmax	Tmax,s-c	εmax	ΔTmax	ΔTmax,s-c	εΔmax
		K	K	%	K	K	%
c_000	330.12	–	–	10.01	–	–
s_020	329.67	0.45	0.14	9.56	0.45	4.47
s_010	328.85	1.27	0.38	8.74	1.27	12.67
s_005	327.02	3.10	0.94	6.96	3.05	30.48
s_002	323.25	6.87	2.08	3.24	6.77	67.61
c_100	321.01	–	–	1.00	–	–
s_120	321.01	0.01	0.00	0.99	0.01	0.06
s_110	320.99	0.02	0.01	0.98	0.02	0.20
s_105	320.95	0.06	0.02	0.94	0.06	0.60
s_102	320.79	0.22	0.07	0.79	0.21	2.14

On the other hand, for b higher than 5⋅2π/r_o and the lower radial thermal conductivity, deviations in maximal temperature become negligible, though considerable errors persist for the maximal temperature spread, i.e., higher than 5 %. In contrast, cases with higher radial thermal conductivity exhibit low absolute and relative errors, demonstrating that thermal conductivity enhancement mitigates the influence of the spiral geometry.

4. Conclusion

Based on the results of the difference between spiral and circular thermal conductivity, it can be said that it is not required to use the spiral structure in the numerical model with the higher radial thermal conductivity as for realistic values of the gap between spiral layers (b>20⋅2π/r_o) no significant difference can be observed at all in temperature fields. The explanation is that tangential vectors of circles and a spiral at intersection points have almost identical directions for points further than 1 mm from the origin. On the other hand, for very sparse spirals, a significant error occurs (up to 7 K) due to the very effective heat removal along the spiral to the outside of the battery.

These findings highlight the importance of explicitly verifying assumptions in the thermal conductivity tensor, particularly for configurations with low radial thermal conductivity (e.g., when the radial thermal conductivity is more than 100 times lower). Significant deviations were observed even for dense spirals, with relative errors not falling below 4.47%. Such verification is essential to ensure the reliability of simplified numerical models in battery thermal simulations.

Acknowledgments

This work was supported by projects "The Energy Conversion and Storage", funded as project No. CZ.02.01.01/00/22_008/0004617 by Programme Johannes Amos Comenius, call Excellent Research and "Hollow Fiber Heat Exchangers with Reduced Permeability for Smart Cities", funded as project No. 8I24002 by Programme EIG CONCERT by Ministry of Education, Youth and Sports.

Data availability

The data that support the findings of this study are openly available in the Dataset for article Spiral Structure of Cylindrical Batteries and its Importance in Modeling of Heat Transfer at http://doi.org/10.5281/zenodo.14016713, reference number [15].

References