Journal of Fluid Flow, Heat and Mass Transfer (JFFHMT)

ISSN: 2368-6111

On the Assessment of the Modified SSTCCM Turbulence Model to Predict Flow around 3D Delta Wing

Yaser H Alahmadi¹

¹slamic University of Madinah, Faculty of Engineering, Department of Mechanical Engineering
Abo Bakr Al Siddiq, Al Jamiah, Madinah 42351, Saudi Arabia
yhalahmadi@iu.edu.sa

Abstract - Various turbulence models have been developed to simulate aerodynamic flows. The eddy viscosity models (EVMs) are commonly implemented to close the Reynolds Averaged Navier-Stokes (RANS) equations, allow them to be the most popular choice for solving aerodynamic problems. EVMs are particularly valued for their robustness and computational efficiency. However, the objectives of achieving both robustness and accuracy in turbulence model development remain a formidable challenge. This study evaluates the performance of a recently developed EVM model in analysing external flows around the NACA0012 airfoil and a 3D Delta wing. Specifically, it examines the effectiveness of the Shear Stress Transport Model with Curvature Correction Modification (SSTCCM) in predicting the flow characteristics of external aerodynamic configurations. Earlier investigations have demonstrated the capability of the SSTCCM model to accurately predict confined swirling flows, such as those in cyclone separators, rotating lids, and sudden expansions. However, the model has yet to be tested in cases involving external flows, where aerodynamic geometry greatly affects the flow behaviour. This study investigates the ability of the SSTCCM model to numerically predict the behavior of external aerodynamic flows. The computational results are compared against experimental data and validated against other EVMs models. The findings show that the SSTCCM model offers a competitive alternative in computational efficiency and superior to conventional EVMs models in terms of accuracy. Conventional EVMs failed to predict lift and drag coefficients accurately, particularly near the stall angle of attack. Moreover, the SSTCCM model successfully captured the wing tip vortices in the 3D Delta wing simulations, highlighting its accurate predictive capabilities for complex flow features.

Keywords: CFD, Aerodynamics, SSTCCM, External Flow, NACA 0012, Delta wing.

© Copyright 2025 Authors - This is an Open Access article published under the Creative Commons Attribution License terms Creative Commons Attribution License terms. Unrestricted use, distribution, and reproduction in any medium are permitted, provided the original work is properly cited.

Date Received: 2024-03-21
Date Revised: 2024-12-05
Date Accepted: 2024-01-06
Date Published: 2025-01-20

1. Introduction

Flow around airfoil and 3D wings is a classical benchmark cases in fluid dynamics. The advancement in computational power leads to a rapid increase in conducting numerical simulations across multiple industrial applications. The widely used eddy viscosity models (EVMs) are known to be superior to the Direct Numerical Simulation (DNS), the Reynolds Stress Model (RSM) and the Large Eddy Simulation (LES). This is attributed to the fact that DNS, RSM and LES are computationally heavy and not practical for complex application, which allow the EVMs to be the best alternative and more practical to be used as a numerical approach in various industrial application. [1, 2, 3].

Wind tunnel testing and computational fluid dynamics (CFD) are the most widely used approaches to investigate and analyse the aerodynamic forces for external flow around objects. The CFD approach is more practice and more reliable, but it requires knowledge and effort to achieve accurate results. For instance, the appropriate selection of the turbulence model has a significant impact towards the accuracy of the results. Different development in turbulence modelling had been proposed recently, one of these attempts is the developed Shear Stress Transport with Curvature Correction Modification (SSTCCM). The SSTCCM was developed to simulate highly swirling flow in a confined geometry. It was initially proposed by Alahmadi and Nowakowski in 2016 [4], they added a rotation function to the k-ω SST model. The rotation function multiplied by the production term in the transport equation of both the turbulent kinetic energy and the turbulent dissipation rate. The implementation of the rotation function is to overcome the weakness and the limitations of conventional Eddy Viscosity Models (EVMs). They investigated the model by simulation a gas-cyclone separator. The results were compared with experimental measurement and verified against other EVMs. The results showed superiority of the SSTCCM over standard EVMs. In 2021, Alahmadi et al. conducted an in-depth investigation of the SSTCCM performance by simulating swirling flow with vortex breakdown and comparing its performance with other turbulence models [5]. Their study validated the model against experimental measurements for flows in a confined cylinder with a rotating lid and within a sudden expansion pipe. The findings highlighted the robustness and the accuracy of the model, proving its capability in numerically simulate diverse engineering applications. Nevertheless, its performance in external flow cases, where aerodynamic shapes significantly influence flow behaviour, remained unexplored.

The application of the Boussinesq hypothesis in Eddy Viscosity Models (EVMs) assumes isotropic eddy viscosity, a simplification that fails to hold for complex, highly swirling flows. While numerous modifications have been proposed to address this limitation, many lack the versatility required for 3D flows [6, 7, 8].

Spalart and Shur [9], and Knight and Saffman [10], proposed empirical adjustments to EVMs to account for the effects of rotation and strong curvature. Spalart and Shur’s approach stands out for its efficiency, as it captures the influence of invariant turbulence components and offers a unified framework for handling curvature and rotation effects. This modification allows it to be suitable for 3D flow applications. Similarly, Hellsten enhanced the k-ω SST model by integrating system rotation and streamlined curvature effects [11]. Hellsten’s modification involved redefining the Richardson number (Ri) by substituting the turbulent time scale from the Khodak and Hirsch model [12] with the mean-flow time scale (1/S_ij). This adjustment simplifies the (Ri) calculation, which can be expressed as: .

In 2009, Smirnov and Menter [13] further refined the k-ω SST model by incorporating Spalart and Shur’s rotation-curvature correction term [9]. Their enhancement targeted the correction of the production terms in the transport equations of both the turbulent kinetic energy (k) and the turbulent dissipation rate (ω), resulting in the SSTCC model. This modification enhanced accuracy, computational efficiency, and robustness, particularly for flows with strong rotation or curvature. By including curvature corrections, the SSTCC model achieved more precise predictions of flow behavior while reducing computational cost compared to LES and RSM.

In 2013, Zhang and Yang proposed a simpler method for incorporating system rotation and curvature into the Spalart-Allmaras model. Their approach implemented the Richardson number (Ri) to avoid the complex computations associated with the Lagrangian derivatives of the strain rate tensor [14].

This study aims to evaluate the ability of the recently developed SSTCCM model in predicting and simulating external flows. First a 2D NACA 0012 airfoil was selected as a case study due to the availability of many experimental and numerical data for comparison. Then the model was tested on a 3D Delta wing where the formulation of the strong wing vortices was detected.

2. The SSTCCM mathematical formulation

2. 1. Governing equation

The fluid flow in computational fluid dynamics is governed by Navier-Stokes equations (the continuity and the momentum equations)

1. The continuity equation:

(1)

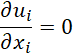
2. The momentum equation:

(2)

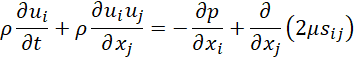
where u, p and μ are the viscosity, the velocity and pressure, respectively. The s_ij term appear on the right-hand side of equation (2) is the strain rate tensor, which is defined as:

(3)

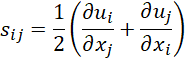
The RANS model is the time averaged of equation (1) and (2), which can be expressed in the following formulations:

1. The time averaged continuity equation:

(4)
2. The time averaged momentum equation:

(5)

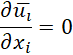
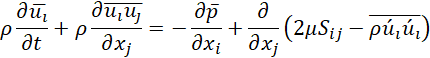
After applying the time averaging technique, a new additional term appears on the RHS of equation (5), which is known as Reynolds stress tensor . Therefore, an additional equation must be implemented to calculate the new term to close the mathematical model. This can be achieved by postulating a specific term of the Reynolds stress tensor in a framework of designing a turbulence model.

2. 2. SSTCCM turbulence model

The conventional k-ω SST model using the Boussinesq hypothesis to relate the Reynolds stress tensor to the turbulent eddy viscosity (μ_t) by the following equation:

(6)

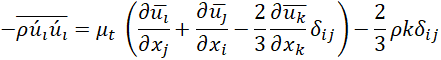
The δ_ij term is the Kronecker Delta operator:

(7)

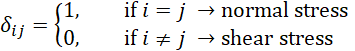
Equation (6) combined both the normal and the shear stress of Reynolds stress tensor. Solving the term μ_t will close the RANS model given in equations (4) and (5). Therefore, μ_t is calculated based on the turbulent kinetic energy k, and the turbulent dissipation rate ω using the following formula:

(8)

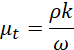
The k-ω SST solve the transport equations of both k, and ω in its framework as a turbulence model to close the mathematical system of the equations.

(9)

(10)

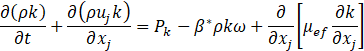
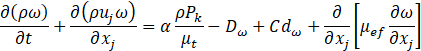
where P_k, β^* and μ_ef are the production of turbulent kinetic energy, model constant and the effective turbulent viscosity, respectively. The term D_ω represents the dissipation of ω, which depends on the turbulence structure and Cd_ω is the cross-diffusion correction term, which is used to improve the model accuracy in boundary layers and free-stream regions.

In the SSTCCM model, the production term in equations (9) and (10) is modified by multiplying it by a rotation function to account for the rotation and curvature effects, and hence they have rewritten as follows:

(11)

(12)

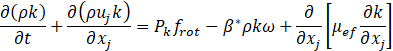
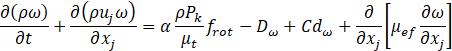
The term f_rot denotes the rotation correction function, which is designed to modify the turbulence equations to incorporate the influences of rotation and curvature. The function f_rot is expressed as:

(13)

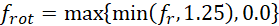
Where f_r is given by:

(14)

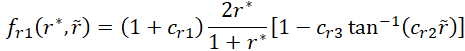
According to Smirnov and Menter [13], equation (13) differs from Eq. (14) by constraining the function within a range of 0 to 1.25. A value of 0 corresponds to strong convex curvature (stabilized flow with no turbulence production), while a value of 1.25 represents strong concave curvature (enhanced turbulence production). The lower limit is implemented to ensure numerical stability, whereas the upper limit is necessary because, unlike the production term in the Spalart-Allmaras (SA) model, which relies on the vorticity tensor Ω, the production terms in the SST model are based on the strain rate tensor S. Since turbulence production based on S is generally higher than that based on Ω, the limiter is essential to prevent excessive eddy viscosity in flows characterized by destabilizing curvature or rotation. The chosen upper limit of 1.25 provided the optimal balance across the two cases examined in this study. Assuming all variables and their derivatives are defined relative to the calculated reference frame, which rotates with a rate Ω, the arguments of function (14), r^*and are defined as follows:

(15)

(16)

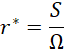
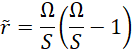
where the strain rate tensor S and the vorticity tensor Ω are given by:

(17)

(18)

(19)

(20)

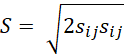
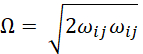
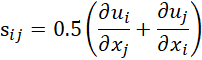
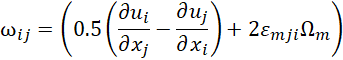
where ε_mji is the Levi-Civita and Ω_m is the component of the angular velocity vector due to rotating reference frame. Based on the numerical tests performed in reference [13], the values of the empirical constants in equation (14), c_r1, c_r2 and c_r3 are set to 1.0, 2.0 and 1.0.

3. Numerical method and simulation setup

3. 1. Solver and algorithm

The SSTCCM turbulence model was implemented using the open-source platform OpenFOAM 2.4.0 [15]. OpenFOAM employs the finite volume method for spatial discretization, and an unsteady solver was utilized to model the incompressible flow field. The simulations were conducted using the PIMPLE algorithm, which couples the velocity and pressure fields. The PIMPLE algorithm combines the features of the PISO and SIMPLE algorithms, making it well-suited for transient fluid flow simulations [16].

3. 2. Grid generation and numerical settings

The accuracy and computational efficiency of numerical simulations mainly depend on the quality and resolution of the grid. Meshes can be categorized as structured, semi-structured (hybrid), or unstructured. Numerical errors in simulations often stem from the shape and size of grid cells, while computational costs are primarily influenced by grid resolution.

Key parameters for evaluating mesh quality include skewness, cell orthogonality, and aspect ratio. Generating structured meshes for complex geometries, such as the sharp trailing edge of an airfoil, can be particularly challenging. These complexities often necessitate additional mesh refinement to address non-orthogonal faces. To handle such issues and enhance computational stability, a non-orthogonal corrector sub-algorithm was applied to improve calculations in regions with non-orthogonal cells. These settings are utilized for both cases, the 2D airfoil and the 3D delta wing.

For the 2D airfoil, a grid-independence study was conducted to determine the optimal grid resolution. Three different grid sizes were tested, as summarized in Table 1. The results showed that while denser grids had minimal impact on the accuracy of the lift coefficient (C_L) calculations, they significantly increased the number of non-orthogonal faces, leading to higher computational costs without corresponding benefits.

Table 1. The lift coefficient  for different grid sizes.

Grid Size	Non-orthogonal	orthogonal corrector	CL
78,256	153	1	0.812525
120,200	257	2	0.854006
400,145	894	4	0.854462

For the simulations discussed in the following sections, the medium-sized mesh, consisting of 120,200 cells, was adopted. The computational domain of the flow and the configuration of the grid is presented in Figure 1.

The simulation was performed at Reynolds number of Re = 3.92×10⁵, based on the chord length with the dynamic viscosity ν set to 1.568 × 10^-5 m²/s. A Dirichlet boundary condition was applied at the inlet, specifying an inlet velocity of U_in = 51 m/s. No-slip conditions were applied to the fixed walls, and zero-gradient conditions were enforced at the outlet. A detailed summary of all boundary conditions used in the simulations is provided in Table 2.

Table 2: The boundary conditions setup.

Boundary	U	P	K	W	Vt
Inlet	(ux,0,0)	zero gradient	2⁄3 (IU)^2	5U⁄L	k⁄ω
Outlet	zero gradient	0	zero gradient	zero gradient	zero gradient
Wall	(0,0,0)	zero gradient	0	10 * 6v/β1 (∆y)2	0
Airfoil or Wing	(0,0,0)	zero gradient	0	10 * 6v/β1 (∆y)2	0

4. Numerical results

4. 1. NACA 0012 airfoil

To evaluate the performance of the SSTCCM model in predicting external flows, simulations were conducted for the 2D NACA 0012 airfoil at various angles of attack (α). Experimental data for validation were taken from Ladson [17]. Figures 2 and 3 present a comparison of the numerical predictions with experimental data for the lift and drag coefficients across different angles of attack. The results indicate that the k-ϵ model performs poorly, as it overpredicts the lift coefficient while underestimating the drag coefficient. Other models show improved accuracy, particularly within the linear region of the lift coefficient (C_L) against the angle of attack (α). However, notable deviations between the simulations and experimental results emerge near the stall angle.

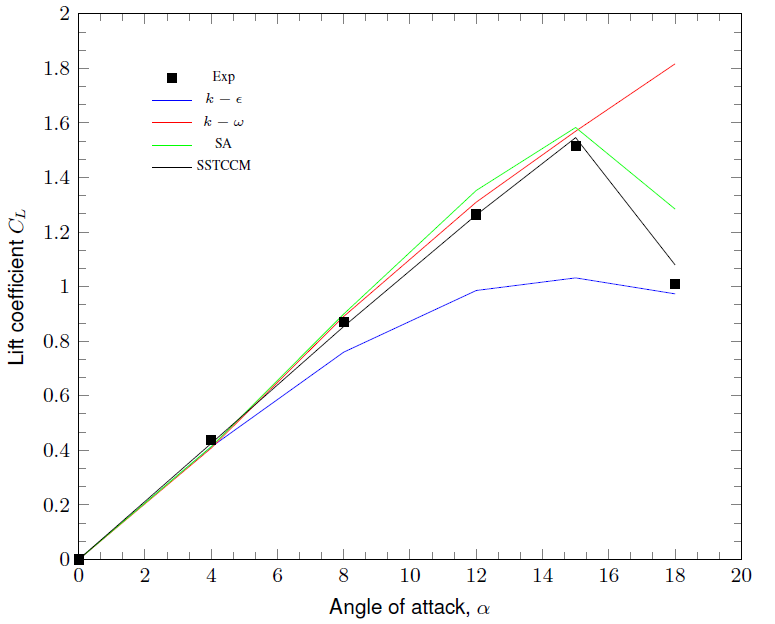
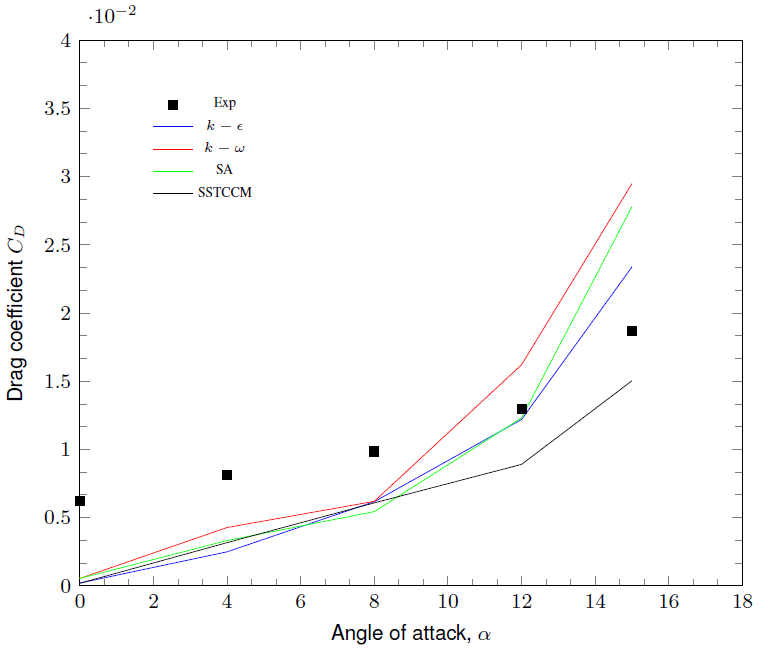
Among the models tested, the SSTCCM model exhibits the closest agreement with experimental data, particularly for the lift and drag coefficients. Conversely, the Spalart-Allmaras (S-A) model slightly overestimates the maximum lift coefficient (C_{L_max}). Other models, such as the SST k-ω model, struggle to capture the stalling behavior accurately at higher angles of attack, whereas the SSTCCM model shows superior performance in predicting lift coefficients. For drag coefficient validation, RANS simulations generally underestimate the drag coefficient in pre-stall conditions. Near an angle of attack of 12°, just before stall, the k-ϵ and S-A models predict the drag coefficient with greater accuracy, while the SST k-ω and SSTCCM models are less precise in this range. Significant flow separation in the stall region introduces instability and vortex generation, making accurate predictions more challenging. In this phase, a notable disparity is observed between computational and experimental data. The aerodynamic coefficients were derived as averages from the final time step of the simulation, as illustrated in Figure 5, which depicts the averaging process for the drag coefficient at α = 4° using the SSTCCM model.

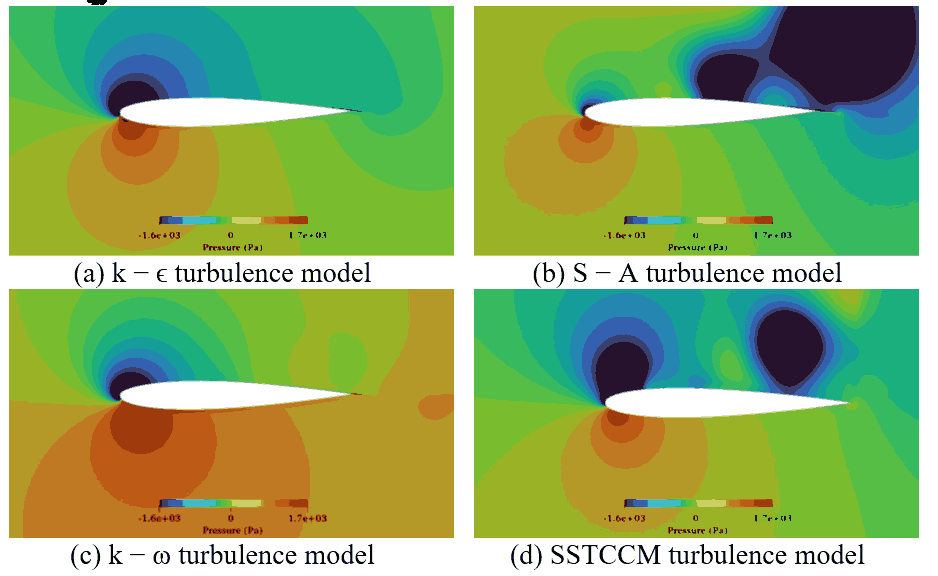
Pressure contours at α = 18° is shown in Figure 4. Under pre-stall conditions, all models produce similar pressure distributions. As the angle of attack approaches the stall region, the SSTCCM model demonstrates improved accuracy in predicting pressure distributions, resulting in reduced errors in aerodynamic force predictions. With the exception of the k-ϵ model, all turbulence models were performing good compared to the experimental measurements.

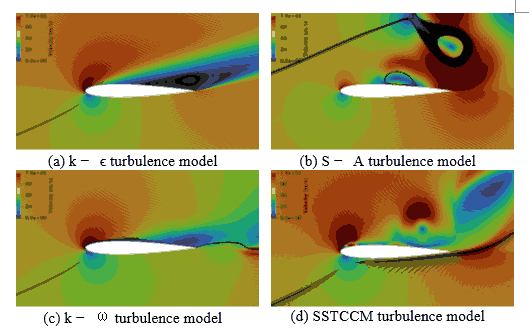
At post-stall conditions, the SSTCCM model maintains its accuracy in predicting pressure distributions, consistent with its performance during the stall. Figure 5 shows velocity contours and streamlines for post-stall condition. The SSTCCM model provides the most accurate representation of flow separation among the models, leading to the best alignment with experimental results. The SST k-ω and S-A models perform reasonably well in most scenarios but encounter difficulties accurately predicting flow behavior at α = 18°.

4. 2. Delta Wing 3D

The choice of the delta wing configuration is motivated by its ability to serve as a benchmark case for studying and investigate fundamental fluid dynamics phenomena, such as vortex breakdown and wing tip vortices, which significantly impact the performance of delta-wing aircraft [18, 19].

Flow simulations of delta wings at high angles of attack present unique challenges due to the complex and unconventional characteristics of the flow, including strong vortices. These complexities often make achieving accurate numerical predictions difficult, particularly in designing turbulence models. To address these challenges, a range of computational fluid dynamics (CFD) methodologies are developed and documented [20-24]. These attempts try to ensure that the CFD tools used for such analyses are optimized and validated for handling this specific class of flow problems.

The delta wing configuration used in this study is that of Polhamus [20]. The computational domain is demonstrated in figure 6.

In this case study, for all the angles of attack the medium grid size with 4,386,975 cells was used as a more refined mesh provides insignificant impact to the accuracy of the predicted lift coefficient. The setup of the boundary conditions is given in table 2. The inlet velocity is u_in=20 m/s. The Reynolds number is based on the mean aerodynamic chord which is corresponding to Re =1.3 ×10⁵. Due to limited computational resources, the simulations were performed at four angles of attack (α=0°,5°,10° and 20°).

Figure 7 demonstrates the streamlines at different angles of attack, it shows the flow behaviour around the wing at different angles of attack, illustrating the progression from smooth flow to complex vortex structures. When α=0°, the flow passes over the wing without significant disturbance, and no vortex formation is observed at the wing tips due to the minimal pressure difference between the top and bottom surfaces. As the angle of attack increases (α=5°,10° and 20°), the pressure difference becomes more pronounced. This creates strong vortices at the wing tips, driven by spanwise flow and pressure gradients. These wing-tip vortices become stronger with increasing α, indicating the growing influence of rotational flow features. The SSTCCM successfully captures these phenomena, including the transition from smooth flow to vortex formation, highlighting its effectiveness in modelling swirling and rotational flows. These results are crucial for understanding aerodynamic behaviour, particularly in evaluating the role of wing-tip vortices, which contribute to induced drag and significantly affect the aerodynamic performance of the wing.

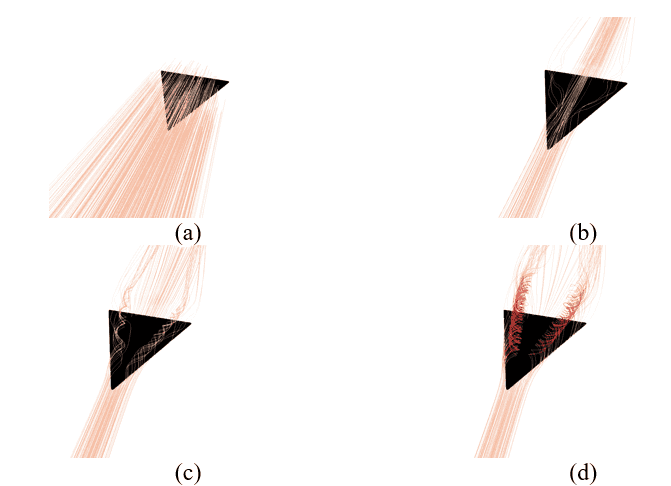
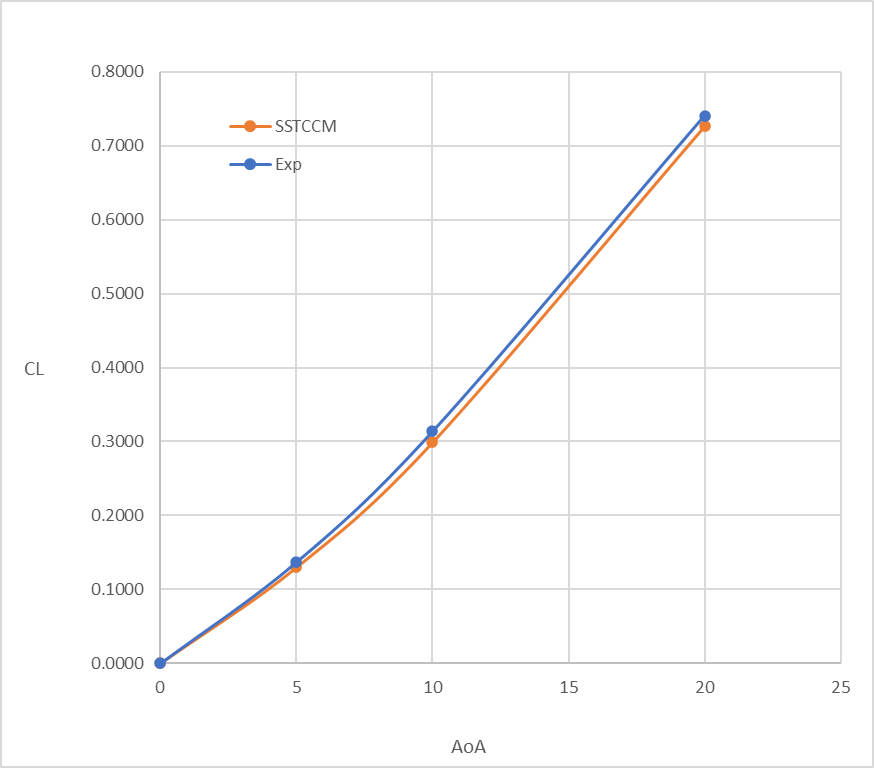
Figure 8 compares the numerical predictions of the lift coefficient with the experimental measurements for validation which were taken from Peckham [22]. The numerical results show the accuracy of the SSTCCM model, where the numerical error is approximately 6%, and that is highly acceptable for CFD simulations involving complex 3D flows. The close agreement between numerical and experimental results highlights the reliability of the SSTCCM model in predicting aerodynamic forces such as lift force. The lift coefficient results also confirm the capability of the model to resolve critical flow features, such as the interaction between lift generation and the development of vortices at higher angles of attack. The numerical simulations provide a precise representation of the aerodynamic forces, ensuring that the lift, drag, and overall aerodynamic performance are accurately captured. These findings highlight the robustness and reliability of the SSTCCM model, making it a valuable model for studying complex aerodynamic systems, optimizing wing designs, and improving performance predictions in both research and practical engineering applications.

6. Conclusion

The present study investigated the performance of a modified Shear Stress Transport model with curvature correction (SSTCCM) in predicting aerodynamic flows. The primary objective was to evaluate the model's capability to simulate complex external flow features. To this end, the SSTCCM was applied to two test cases: a 2D NACA 0012 airfoil and a 3D delta wing. Notably, this work represents the first implementation of the SSTCCM model for external aerodynamic flow simulations.

The results demonstrated excellent agreement between numerical predictions and experimental measurements, validating the model’s accuracy. For the 2D NACA 0012 airfoil, the SSTCCM accurately predicted aerodynamic forces, such as the lift coefficient (C_L) and drag coefficient (C_D). For the 3D delta wing, the model successfully captured the wing-tip vortex structures and showed reliable predictions of the aerodynamic forces, particularly the lift coefficient, when compared to experimental data.

The SSTCCM model exhibited superior performance compared to conventional eddy viscosity models (EVMs), excelling in accuracy, robustness, and computational efficiency. Key findings from the study include:

• The SSTCCM model demonstrated higher accuracy than traditional EVMs for predicting flow characteristics in both 2D and 3D cases.
• It effectively captured the complex wing-tip vortex structures in the 3D delta wing flow, addressing a significant challenge for conventional EVMs.
• The SSTCCM model preserved the accuracy of its predecessor while significantly improving computational efficiency, reducing CPU time compared to Reynolds Stress Models (RSM).

These findings position the SSTCCM model as a robust and efficient numerical tool for simulating complex external aerodynamic flows, offering a valuable alternative to existing turbulence models.

Acknowledgments

The author would like to express his appreciation for the support provided by the Scientific Research Deanship, Islamic University of Madinah, Kingdom of Saudi Arabia.

References