Volume 11 - Year 2024 - Pages 311-321
DOI: 10.11159/jffhmt.2024.031
Study In Transient Regime Of A Silicon Solar Cell: Influence Of Temperature And Magnetic Field
Pape Diop1, Mamadou Lamine Samb2, Dibor Faye1, Mame Malick Diop1
1Cheikh Anta Diop University of Dakar, Physics Departement
Dakar-Fann, SN
Pape7.diop@ucad.edu.sn; diopp504@gmail.com, faye.dibor@ucad.edu.sn
2Iba Der Thiam University of Thiès, Sciences & Technology Department
Grand Standing, behind C3S Thiès, Thiès, SN
mlsamb@univ-thies.sn
Abstract - A study of the effect of temperature and magnetic field on the transient decay of the excess minority carrier density and on the electrical parameters in the base of a parallel vertical junction solar cell, in transient dynamic regime operation, and under polychromatic illumination is presented. The experimental device that allows us to have the transient regime and its operating principle is presented. The resolution of the continuity equation of the minority carriers of charges in the base and the determination of the eigenvalues make it possible to determine the transient density which is a sum of infinite terms and whose time of decay of the various harmonics is studied. The transient voltage, the photocurrent density and the transient capacitance of the solar cell are deduced from the expression of the transient density of minority carriers of excess charges in the base. Indeed, the influence of the optimum temperature on the amplitudes and on the transient decrease of these electrical parameters is also studied. This optimum temperature is obtained by determining the optimum thickness of the solar cell from a given magnetic field. Indeed, as the temperature increases, there will be thermal agitation resulting in an accumulation of carriers at the junction and therefore a reduction in carrier mobility. If there is thermal agitation, the minority carriers will take longer to cross the junction. The stationary regime will therefore be reached late, hence t0 increases with the increase in temperature. This work allowed us to observe that in the first moments of decay, the diffusion capacity is minimal, which leads to a rapid but brief drop in amplitudes because with a recombination velocity in short-circuit, a large number of Minority charge carriers in the base pass through the space charge region to participate in photocurrent generation.
Keywords: Solar Cell, Vertical Parallel Junction, Magnetic Field, Temperature, Time Constant, Base Thickness, Transient Voltage, Photocurrent and Transient Capacity.
© Copyright 2024 Authors - This is an Open Access article published under the Creative Commons Attribution License terms. Unrestricted use, distribution, and reproduction in any medium are permitted, provided the original work is properly cited.
Date Received: 2023-10-18
Date Revised: 2024-07-29
Date Accepted: 2024-08-15
Date Published: 2024-09-30
1. Introduction
The Silicon solar cells being under different technologies [1], present in different architectures, such as solar cells with vertical junctions (connected in series or parallel) where the illumination takes place parallel to the junction plane [2]-[3].
By taking into account certain physical mechanisms, modeling work [4]-[11] has been done for the search for geometric dimensions, thus leading to a better efficiency of the solar cell. Two types of vertical Multi Junction (MJV) silicon solar cells [12]-[13] have been developed: (n/p) cells connected in parallel to increase the electric current (MJVP) and (n/p) cells p/p+) connected in series to increase the electrical output voltage (MJVS).
These solar cells can be under different operating regimes, which are: the transient dynamic regime [14]-[17]. Under these operating regimes, the solar cell may be subject to external conditions, which may be: electromagnetic field variations [18]-[22], temperature variations [23]-[24], etc…
In regards to the transient regime, we can note the influence of the magnetic field [25] and/or the temperature [26] on the transient decay and on the decay time of the minority charge carriers.
This study was done on a silicon solar cell (n/p) with vertical junctions connected in parallel under the double condition of temperature and magnetic field, and in operation of transient dynamic regime which occurs between two stable states from operating points dependent on two variable resistors. We examine the effects of the magnetic field [27]-[28], the temperature [29]-[30] and the optimal thickness [5], [31] on the eigenvalues ωn of the different harmonic states and on the time t0 initiating the exponential decay and on the transient decay of electrical parameters.
2. Materials and Methods
2.1. Experimental Setup and Working
Figure 1 presents the experimental device used to obtain the transient state by variations of the operating point of the solar cell [16]-[17].
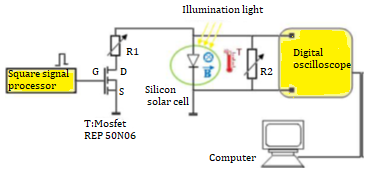
This experimental device includes a square signal generator (BRI8500) which supplies an RFP50N06 type MOSFET transistor, two adjustable resistors R1 and R2, a silicon solar cell placed under temperature and magnetic field which submitted to multi-spectral lighting, a digital oscilloscope, a microcomputer for signal acquisition and processing. The transient decay occurs according to the following procedure, described below.
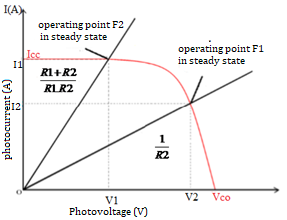
At time t<O (figure 1), the solar cell being under constant multi-spectral illumination, the MOSFET transistor opened and the solar cell is closed in series with the resistor R2 alone: this corresponds to the operating point F2 in steady state [ 32]-[33] giving the potential V2. At t=0 (figure 1), the closing of the MOSFET begins and after a very short time the MOSFET is completely closed, then the resistor R1 is in parallel with R2. This corresponds to the operating point F1 in steady state, so the voltage V2 drops from V2 to V1. The transient voltage at the terminals of the solar cell is recorded by a digital oscilloscope (Tektronics) which then transmits it to a microcomputer for processing and analysis.
By varying R1 and R2, the steady state operating points F1 and F2 move over the I-V characteristic (Figure 2), to produce a transient state.
2.2 Theory
In figure 3, the structure of the (n/p) silicon solar cell with vertical junctions connected in parallel under magnetic field and temperature is presented.
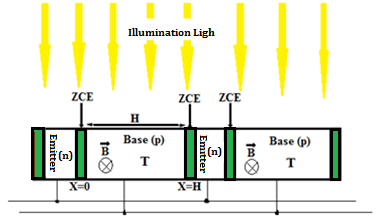
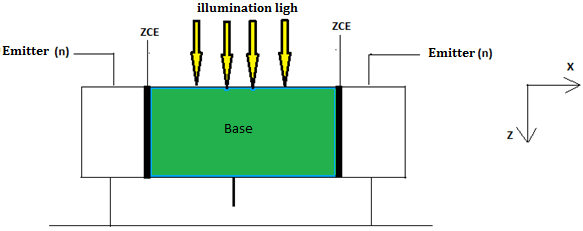
The illumination was assumed to be uniform, such that the carrier generation rate depended only on depth (z) in the base and was expressed as:
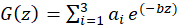
The coefficients ai and bi are obtained through tabulated values of the radiation [34].
During the experiment, the level of illumination remains constant, which implies that the level of injection is not modified with respect to time. On the magneto-transport equation [20] and [36] in dynamic regime, related to excess charge carriers δ(x, t) [3] in the base at temperature (T) [23]:
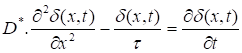
The diffusion coefficient D* of the minority carriers in the base under the influence of the temperature T and the applied magnetic field B, is given by the relationship [35]-[36]:
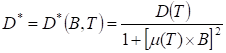
B is the magnetic field in the base.
τ is the average lifetime of minority carriers in the base.
μ(T) is the mobility of excess minority carriers in the base [37].
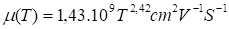
The diffusion coefficient of the minority carriers of charge in the base, dependent on the temperature D (T) without magnetic field is given by the relation of Einstein-Smoluchowski:
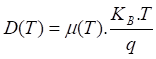
Where Kb is the Boltzmann constant Kb = 1.38.10-23 m2 kg s-2 K-1 and q the elementary charge of the electron.
The equation is solved using the following boundary conditions:
- at the junction x=0:
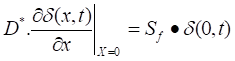
- In the middle of the base:
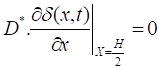
Sf is the recombination velocity of the minority charge carriers at the junction [17], [38]-[39] and defines the operating point of the solar cell [32]-[33] on its I-V characteristic.
The system of equations (2), (6) and (7) constitutes a problem of Sturm Liouville [40] whose solutions are with separable variables of the type:
X(x) represents the spatial function of the minority carrier density and T(t) the temporal function.
X(x) and T(t) take the following forms respectively:
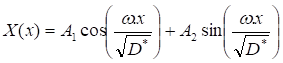
A1 and A2 are coefficients to be determined
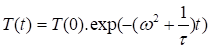
With ![]() (11), the decay time constant and where ω > 0.
(11), the decay time constant and where ω > 0.
The application of the boundary conditions (6) and (7) give respectively the relations (12) and (13):
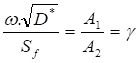
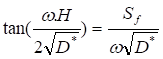
Equation (13) is a transcendental equation whose solutions are determined graphically. With:
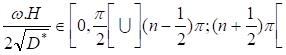
The first interval ![]() suit for n=0 and the second for n >0, n is a natural number.
suit for n=0 and the second for n >0, n is a natural number.
When n=0, we have the first term ![]() that corresponds to the fundamental state with the eigenvalue. And for n >0, we have the different
that corresponds to the fundamental state with the eigenvalue. And for n >0, we have the different ![]() harmonics of order n of eigenvalues .
harmonics of order n of eigenvalues .
A1 and A2 are calculated using the normalization conditions and the Fourier transformation.
The expression of Tn (0) is calculated using the excess minority carrier density in the static regime.
The expression of δ(x, t) is therefore written:
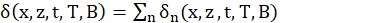
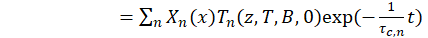
The excess minority carrier density in the base is given by relation (16).
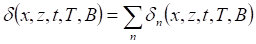
![]() is called decay time constant, its inverse can be written:
is called decay time constant, its inverse can be written:
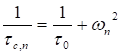
After the graphical resolution of the transcendental equation 13, we put on the board the solutions of this equation corresponding to the eigenvalues of the different harmonic states. They are the points of intersection of the tangential part and the non-tangential part of this equation.
To calculate the errors and uncertainties on the values of 𝜔, we need to account for the uncertainties in the different parameters (T, B and D).
The uncertainty in 𝜔 can be calculated using the error propagation method:
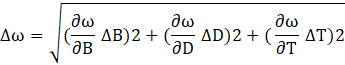
Table 1 Table of eigenvalues ωn for different values of Top, Hop and B
|
T(K) |
254.7 |
286.6 |
313 |
336.5 |
361.4 |
381.9 |
410 |
418.8 |
|
B(T) |
0.0003 |
0.0004 |
0.0005 |
0.0006 |
0.0007 |
0.0008 |
0.0009 |
0.001 |
|
Hop (cm) |
0.0161 |
0.0156 |
0.0153 |
0.0149 |
0.0147 |
0.0146 |
0.01445 |
0.0143 |
|
ω0 |
3077 |
2944 |
2832 |
2774 |
2704 |
2619 |
2565 |
2517 |
|
ω1 |
7306 |
4945 |
4752 |
4644 |
4519 |
4396 |
4301 |
4219 |
|
ω2 |
9468 |
6973 |
6694 |
6536 |
6353 |
6171 |
6033 |
5926 |
|
ω3 |
11650 |
9024 |
8651 |
8444 |
8206 |
7962 |
7786 |
7642 |
| Δω |
0.97 |
0.85 |
0.76 |
0.58 |
0.52 |
0.43 |
0.39 |
0.36 |
Thus, based on the above data, the uncertainty in the eigenvalue 𝜔 indicates that the parameters are very well adjusted and that the results obtained are very close to the true value.
The transient decay of fundamental mode corresponds to n = 0 and that of others correspond to the different harmonics n (with n ≠ 0).
We find that the eigenvalues ωn of the different harmonics decrease with increases in the optimum temperature of the magnetic field and the optimum thickness.
3.Results and Discussion
3.1. Transient Excess Minority Carriers Density
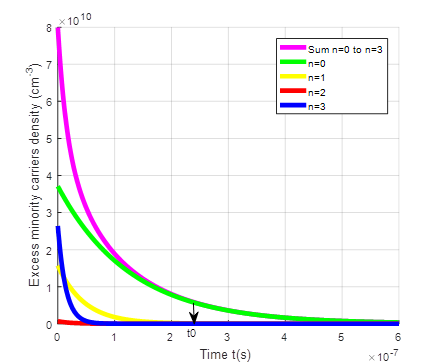
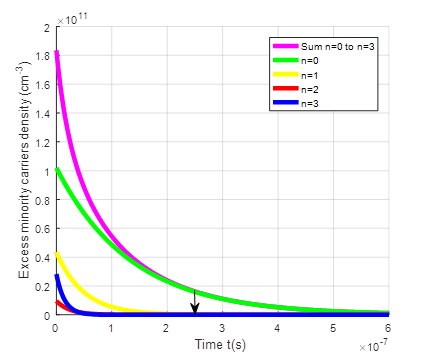
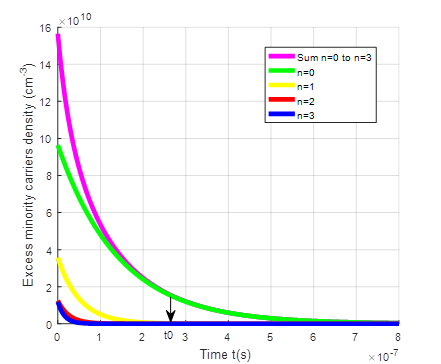
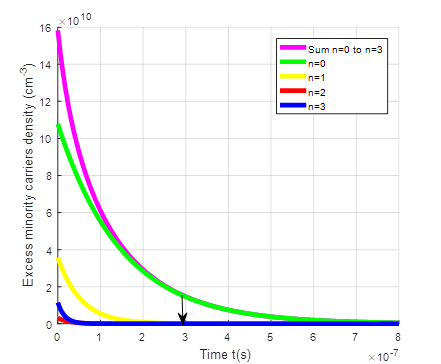
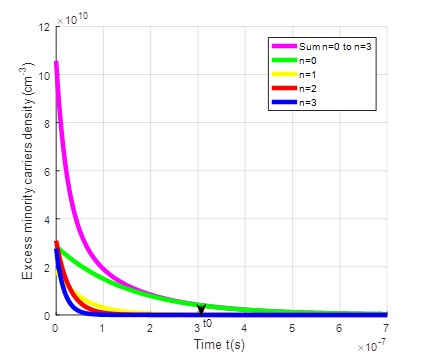
The eigenvalues ωn allowed us to plot the profiles of excess minority carrier the transient δ(x, t) and as well as those of the different harmonics using the results of the optimal thickness of the base (Hopt) [27]-[28] for different magnetic fields (B) and values of the optimum temperature, border between the normal phenomena and the Umklapp process [36].
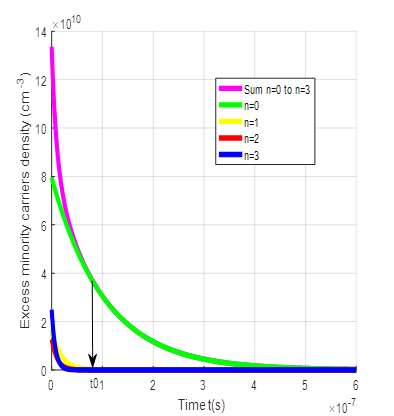
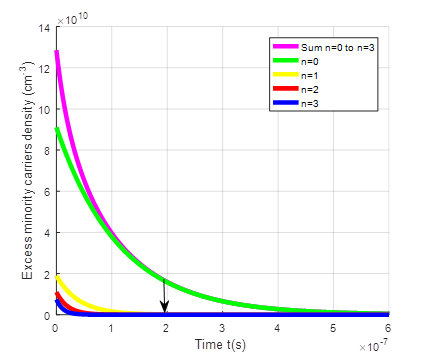
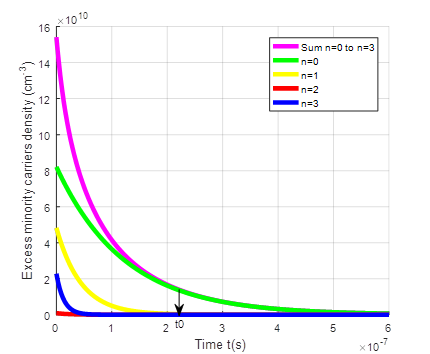
The following figures represent the evolution of the transient excess minority carriers density δ(x, t) corresponding to the sum of the density at the fundamental mode and the various other harmonics (n<4) in terms of (Hopt), of the magnetic field (B) and of (Topt).
To estimate the uncertainty in the decay time t. The error in t can be estimated using error propagation from the exponential relationship T(t)=T(0) e-(ω2+1/τ)t
The total uncertainty in t can be expressed as:
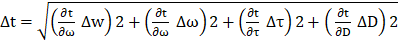
For example, if T=254.7K; B=0.0003T and Hop=0.0161cm, the uncertainty in t is Δt=0.088ns The uncertainty Δt is small compared to the central value t, which demonstrates a high level of precision in the calculation. Which is crucial for optimising performance and making decisions based on these analyses.
We note on the figures above that the transient excess minority carriers density δ(x, t) being the sum of the various harmonic of order n density, decreases to reach the final steady state. It is the same for the fundamental mode density and the other harmonics of order n density. However, it should be noted that after a time t0, the transient excess minority carrier density δ(x, t) is equal to the contribution of fundamental mode density while the other harmonics (n≠ 0) density quickly tend to steady state.
t0 is the time after which the excess minority carrier density corresponding is equal to the contribution of fundamental mode density. This point marks an important stage in the response of the solar cell, as it indicates that the transient effects have evolved to a level comparable to the equilibrium condition. Some values of t0 are given in table 2 below.
Table 2:- Some values of t0
|
T(K) |
254.7 |
286.6 |
313 |
336.5 |
361.4 |
381.9 |
410 |
418.8 |
|
B(T) |
0.0003 |
0.0004 |
0.0005 |
0.0006 |
0.0007 |
0.0008 |
0.0009 |
0.001 |
|
Hop (cm) |
0.0161 |
0.0156 |
0.0153 |
0.0149 |
0.0147 |
0.0146 |
0.01445 |
0.0143 |
|
t0 (10-7s) |
0.81 |
1.95 |
2.24 |
2.38 |
2.51 |
2.78 |
2.95 |
3.02 |
Indeed, as the temperature increases, there will be thermal agitation resulting in an accumulation of carriers at the junction and therefore a reduction in carrier mobility. If there is thermal agitation, the minority carriers will take longer to cross the junction. The stationary regime will therefore be reached late, hence t0 increases with the increase in temperature.
However, it should be noted that the time t0 in short circuit is smaller than that of open circuit [26]. This may be explained by the fact that with the velocity of recombination Sf in short circuit, the photogenerated charge carriers have sufficient energy which allows them to cross the junction very quickly compared to the charge carriers in open circuit.
Indeed, by increasing the magnetic field, we increase the optimum temperature and consequently reduce the probability of diffusion of carriers, which explains the slowing down of the decay with the increase in the field which is also dependent on the increase in the optimum thickness of the base. But this slowing down is less strong in short-circuit because of the high recombination of velocity at the junction.
3.2. Transient Voltage
The expression of the voltage collected at the terminals of the solar cell when it submitted to polychromatic illumination is obtained from the Boltzmann relationship; it is expresses in the form:
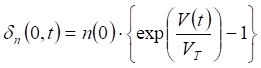
V (t) is the Transient Voltage.
VT is the thermal voltage
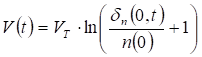
After resolution, the transient voltage becomes:
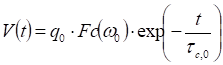
With
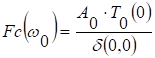
The following figures represent the evolution of the transient voltage as a function of (Hopt), of the magnetic field (B) and of (Topt).
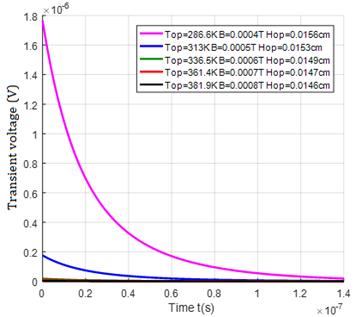
Figure 13 shows that the transient voltage decreases in amplitude as the temperature and magnetic field increase respectively. In addition, thermal agitation increases the intrinsic carrier density at the junction, reducing the voltage and increasing the transient decay as the optimum temperature increases.
The voltage amplitude obtained in the vicinity of the short-circuit is much lower than that obtained in the vicinity of the open circuit. Since the velocity recombination at the junction in the vicinity of the short-circuit is greater than that of the open circuit, there will be fewer and fewer carriers near the junction, so the short-circuit voltage will be reduced as the velocity recombination at the junction increases.
3.3 Transient photocurrent density
The photocurrent is due to the diffusion of minority charge carriers at the junction. Knowing the expression for the minority carrier density, we can determine the expression for the photocurrent density using FICK's law.
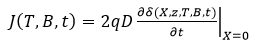
Figure 14 represents the profile of the transient photocurrent density as a function of time in the vicinity of the short circuit for different values of Top, Hop corresponding to a given magnetic field.
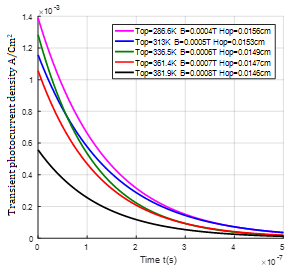
By studying the short-circuit photocurrent density profiles, the first instants of decay result in a rapid drop in the amplitude of the current intensity because they are dominated by the diffusion of minority charge carriers. This is followed by a period of slower decay, which is also linked to the recombination of minority carrier photogenerated in the base.
Indeed, the more the temperature increases, the more there is thermal agitation which widens the space charge zone [5]. As a result, with the very high velocity in short circuit recombination, a large number of carriers will be able to cross the junction to participate in the photocurrent so the stationary regime will therefore be reached late unlike the open circuit situation.
3.4 Transient capacity
The space charge region of a solar cell can be considered as a planar capacitor [7]-[8] called the transition capacitance. This diffusion capacitance of the solar cell is considered to be the capacitance resulting from the variation in charge during the diffusion process within the solar cell [9]-[10]. It is given by the relationship:
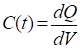
Q is the charge in the vicinity of the emitter-base junction:
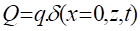
Taking into account the expression for the photovoltage and the density of minority carriers, we obtain the following expression:
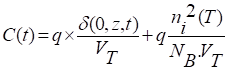
The first term in the expression is the diffusion capacity of the solar cell at temperature T and magnetic field B under polychromatic illumination.
The second term in the expression is the capacitance under darkness: it depends on the nature of the material through the intrinsic concentration of minority ni carriers, the doping of the material (NB), the temperature T and the Boltzmann constant (Kb) in the expression of the thermal voltage VT.
Figure 15 represents the profile of the Transient Capacity in the vicinity of the short circuit as a function of Time for different values of the Top Temperature, the Hop thickness and the magnetic field.
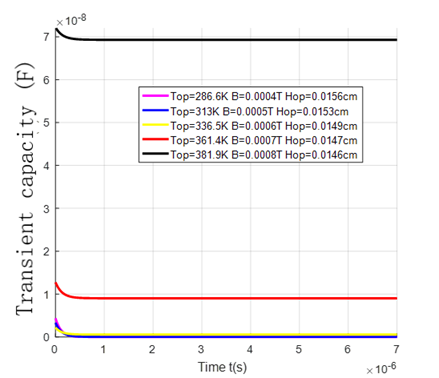
We note in the first moments of decay that the diffusion capacity is minimal, which leads to a rapid but brief drop in amplitudes because with a high velocity of short-circuit recombination, a large number of minority charge carriers in the base crosses the space charge zone to participate in the generation of the photocurrent.
There follows a long period where the capacity tends towards the final stationary regime which is linked to the recombination phenomena of the minority carriers photogenerated in the base.
We also observe that the diffusion capacity decreases with increases in the optimum temperature of the magnetic field and the optimum thickness. Increasing the magnetic field leads to a disordered displacement of the carriers, which in turn increases the number of stored carriers. As a result, this minimal diffusion will lead to an increase in the amplitude of the transient capacity as the magnetic field increases.
4. Conclusion
This work allowed us to see the effect of temperature and magnetic field on the eigenvalues, on the transient decay of the excess minority carrier density in the base, on the transient decay of electrical parameters of a silicon solar cell with vertical junction in parallel placed in short-circuit, in transient operation. The graphical resolution of the transcendent equation has been carried out. It allowed us to find the eigenvalues, then to plot the profile of the minority carrier density, and finally to find the decay time t0 dependent on the optimal temperature and therefore on the optimal thickness. These eigenvalues are then used to plot the profile of transient photovoltage, photocurrent density and transient capacitance which are deduced from the expression for the density of minority charge carriers. Under increasing magnetic field and temperature we have derived the following results:
- The transient voltage and photocurrent density tend rapidly towards stationary regime.
- The diffusion capacity of minority carriers decreases, leading to an increase in the amplitude of the transient capacity and a very brief decay.
References
[1] M. A. Green. Silicon Solar cells advanced principles & practice Printed by Bridge printer Pty. Ltd. 29-35 Dunning Avenue, Roseberry, Center for photovoltaic Devices and systems, March 1995; pp.29-35
[2] J.F. Wise. Vertical Junction Hardened Solar Cell. US Patent 3, 690-953, 1970.
[3] A. Gover and P. Stella. Vertical Multijunction Solar-Cell One-Dimensional Analysis. IEEE Transactions on Electron Devices, 1974, ED-21, 351-356.
View Article
[4] M.M.S. Dede, M.L. Ba, M.A. Ba, M. Ndiaye, S. Gueye, E.H. Sow, I. Diatta, M.S. Diop, M. Wade, G. Sissoko. Back Surface Recombination Velocity Dependent of Absorption Coefficient as Applied to Determine Base Optimum Thickness of an n+/p/p+ Silicon Solar Cell. Energy and Power Engineering, 12, 445-458 https://www.scirp.org/journal/epe, (2020).
View Article
[5] M.S. Diop, H.Y. Ba, N. Thiam, I. Diatta, Y. Traore, M.L. Ba, E.H. Sow, O. Mballo, G. Sissoko . Surface Recombination Concept as Applied to Determinate Silicon Solar Cell Base Optimum Thickness with Doping Level Effect. World Journal of Condensed Matter Physics, 9, pp.102-111, 2019. https://www.scirp.org/journal/wjcmp
View Article
[6] G. Diop, H.Y. Ba, N. Thiam, Y. Traore, B. Dione, M.A. Ba, P. Diop, M.S. Diop, O. Mballo and G. Sissoko. Base thickness optimization of a vertical series junction silicon solar cell under magnetic field by the concept of back surface recombination velocity of minority carrier. ARPN Journal of Engineering and Applied Sciences Vol. 14, No. 23, pp.4078-4085, 2019.
[7] D. Faye, S. Gueye, M. Ndiaye, M.L. Ba, I. Diatta, Y. Traoré, M. Diop, G. Diop, A. Diao, Grégoire. S. Lamella silicon solar cell under both temperature and magnetic field: width optimum determination journal of electromagnetic analysis and applications, 2020, 12, 43-55 https://www.scirp.org/journal/jemaa
View Article
[8] P.C. Dhanasekaran and B.S.V. Gopalam. Effect of Junction Depth on the Performance of a Diffused n+p Silicon Solar Cell. Solid State Electrons, 24, 1077-1080, 1981. https://doi.org/10.1016/0038-1101
View Article
[9] J.D. Arora, S.N. Singh and P.C. Mathur. Surface Recombination effects on the performance of n+-p step and diffused junction silicon solar cells. Solid State Electronics, 24(8), pp.739-747, 1981
View Article
[10] M.M. Ely , N. Thiam , M. Ndiaye , Y. Traore , R. Mane , E.H. Sow , O. Mballo , M.S. Diop , C.T. Sarr, I. Ly , G. Sissoko. Surface recombination velocity concept as applied to determinate back surface illuminated silicon solar cell base optimum thickness, under temperature and external magnetic field effects. Journal of Scientific and Engineering Research, 7(2):69-77, 2020
[11] N.M.M. Mohamed, O. Sow, S. Gueye, Y. Traore, I. Diatta, A. Thiam, M.A. Ba, R. Mane, I. Ly, G. Sissoko. Influence of Both Magnetic Field and Temperature on Silicon Solar Cell Base Optimum Thickness Determination. Journal of Modern Physics, 10, 1596-1605, 2020. https://www.scirp.org/journal/jmp
View Article
[12]. M. Meusel, W. Benssch, T. Berdunde, R. Kern, V. Khorenko, W. Kostler, G. Laroche, T. Torunski, W. Zimmermann, G. Strobl, W. Guter, M Hermle, R. Hoheisel, G Siefer, E Welser, F. Dimroth, A. W. Bett, W. Geens, C. Baur, S. Taylor, G. Hey. Development and production of European III-V multijunction Solar cells. Proceeding of the 22nd European photovoltaic Solar Energy Conference, 2007. Pp. 16 - 51.
[13] G.E. Ayvazian, G.H. Kirakosyan and G.A. Minasyan. (2004). Characteristics of Solar Cells with Vertical p-n Junction. Proceedings of 19th European Photovoltaic Solar Energy Conference, Paris, 7-11 June 2004, 117-119.
[14] B. Ba, M. Kane, A. Fickou, G. Sissoko. Excess minority carrier densities and transient short circuit currents in polycrystalline silicon solar cells.Solar Energy Materials and Solar cells 31 pp. 33-49 0927-0248 /93/$ 06.00 © 1993 êlsevier Science Publishers B. V.
View Article
[15] K. Joardar, R.C. Dondero and D.K. Schroda. Critical Analysis of the Small-Signal Voltage-Decay Technique for Minority-Carrier Lifetime Measurement in Solar Cells. Solid State Electronics, 32, pp.479-483, 1989.
View Article
[16] P. Mialhe, G. Sissoko, F. Pelanchon, and J. M. Salagnon. Régimes transitoires des photopiles : durée de vie des porteurs et vitesse de recombinaison. J. Phys. III, France 2 pp. 2317-2331, 1992.
View Article
[17] G.Sissoko, S. Sivoththanam, M. Rodot, P. Mialhe. Constant illumination-induced open circuit voltage decay (CIOCVD) method, as applied to high efficiency Si Solar cells for bulk and back surface characterization. 11th European Photovoltaic Solar Energy Conference and Exhibition (Montreux, Switzerland), 1992. Pp. 352-54.
[18] S. Mbodji, M. Zoungrana, I. Zerbo, B. Dieng and G. Sissoko. Modelling Study of Magnetic Field's Effects on Solar Cell's Transient Decay. World Journal of Condensed Matter Physics, 5, 284-293, 2015. doi: 10.4236/wjcmp.2015.54029.
View Article
[19] S. Mbodji, I. Ly, A. Dioum, H. Ly Diallo, I.F. Barro, G. Sissoko. Equivalent electric circuit of a bifacial solar cell in transient state under magnetic field. Proceedings of the 21st European Photovoltaic Solar Energy Conference and Exhibition -Dresden, Germany, 2006, pp.447-450.
[20] Y. Betser, D. Ritter, G. Bahir, S. Cohen, and J. Sperling, "Measurement of the minority carrier mobility in the base of heterojunction bipolar transistors using a magnetotransport method", Appl. Phys. Lett., Vol. 67, No. 13, (1995) p 1883-1884.
View Article
[21] S. Mbodji, A. S. Maiga, M. Dieng, A. Wereme, G. Sissoko. Removal charge technique applied to a bifacial solar cell under a constant magnetic field Global Journal of Pure and Applied Sciences, Vol.15, N°1, pp.125-132, 2009.
View Article
[22] S. Madougou, F. Made, M.S. Boukary and G. Sissoko. I-V Characteristics for Bifacial Silicon Solar Cell Studied under a Magnetic Field. Advanced Materials Research, 18-19, 303-312, 2007.http://dx.doi.org/10.4028/www.scientific.net/AMR.18-19.303
View Article
[23] M. Fall, I., Gaye, D. Diarisso, G. Diop, K. Loum, N. Diop, K. Sy, M. Ndiaye and G. Sissoko. AC Back Surface Recombination Velocity in n+-p-p+ Silicon Solar Cell under Monochromatic Light and Temperature. Journal of Electromagnetic Analysis and Applications, 13, 67-81, 2021. doi: 10.4236/jemaa.2021.135005.
View Article
[24] B.D.D. Sylla, I. Ly, O. Sow, B. Dione, Y. Traore, G. Sissoko. Junction Surface Recombination Concept as Applied to Silicon Solar Cell Maximum Power Point Determination Using Matlab/Simulink: Effect of Temperature. Journal of Modern Physics, 9, 172-188, 2018. http://www.scirp.org/journal/jmp
View Article
[25] S. Mbodji, M. Zoungrana, I. Zerbo, B. Dieng, G. Sissoko. Modelling Study of Magnetic Field's Effects on Solar Cell's Transient Decay. World Journal of Condensed Matter Physics, 284-293, 2015. http://dx.doi.org/10.4236/wjcmp.2015.54029
View Article
[26] P. Diop, S. Gueye, G. Diop, D. Faye, I. Diatta, O.K. Dieng, O. Sow, M. Thiame, M. Wade and G. Sissoko. Influence de la température et du champ magnétique sur la décroissance transitoire de la densité des porteurs de charge dans une photopile au silicium a multi jonctions verticales connectées en parallèle et placée en circuit ouvert. International journal of advanced research. Int. J. Adv. Res. 10(08), 69-82, 2022.
View Article
[27] C. Thiaw, M.L. Ba, M.A. Ba, G. Diop, I. Diatta, M. Ndiaye, G. Sissoko. n+-p-p+ Silicon Solar Cell Base Optimum Thickness Determination under Magnetic Field. Journal of Electromagnetic Analysis and Applications, 12, pp. 103-113, 2020. ISSN Online: 1942-0749 ISSN Print: 1942-0730: https://www.scirp.org/journal/paperabs.aspx?paperid=101717
View Article
[28] G. Diop, H.Y. Ba, N. Thiam, Y. Traore, B. Dione, M.A. Ba, P. Diop, M.S. Diop, O. Mballo and G. Sissoko. Base Thickness Optimization of a Vertical Series Junction Silicon Solar Cell under Magnetic Field by the Concept of Back Surface Recombination Velocity of Minority Carrier. ARPN Journal of Engineering and Applied Sciences, 14, 4078-4085, 2020.
[29] F.M. Ndiaye, M.L. Ba, M.A. Ba, G. Diop, I. Diatta, E.H. Sow, O. Mballo and G. Sissoko. Lamella Silicon Optimum Width Determination under Temperature. International Journal of Advanced Research, 8, 1409-1419, 2020.
View Article
[30] N. Mohamed, O. Sow, S. Gueye, Y. Traore, I. Diatta, A. Thiam, M. Ba, R. Mane, I. Ly and G. Sissoko. Influence of Both Magnetic Field and Temperature on Silicon Solar Cell Base Optimum Thickness Determination. Journal of Modern Physics, 10, 1596-1605, 2019. doi: 10.4236/jmp.2019.1013105.
View Article
[31] M.S. Dede, M.L. Lamine Ba, M.A. Ba, M. Ndiaye, S. Gueye, E.H. Sow, I. Diatta, M. Diop, M. Wade and G. Sissoko. Back Surface Recombination Velocity Dependent of Absorption Coefficient as Applied to Determine Base Optimum Thickness of an n+/p/p+ Silicon Solar Cell. Energy and Power Engineering, 12, 445-458, 2020. doi: 10.4236/epe.2020.127027.
View Article
[32] B. Dione, O. Sow, M. Wade, I. Ly, S. Mbodji, G. Sissoko. Experimental Processus for Acquisition Automatic Features of I-V Properties and Temperature of the Solar Panel by Changing the Operating Point. Circuits and Systems, 7, 3984-4000, 2016 http://www.scirp.org/journal/cs ISSN Online: 2153-1293 ISSN Print: 2153-1285.
View Article
[33] G. Sissoko and S. Mbodji. A Method to Determine the Solar Cell Resistances from Single I-V Characteristic Curve Considering the Junction Recombination Velocity (Sf). Int. J. Pure Appl. Sci. Technol., 6(2), pp.103-114, 2011.ISSN 2229 - 6107 Available online at
View Article
[34] J. Furlan and S. Amon. Approximation of the Carrier Generation Rate in Illuminated Silicon. Solid-State Electronics, 28, 1241-1243, 1985.
View Article
[35] Th. Flohr and R. Helbig. Determination of minority-carrier lifetime and Surface recombination velocity by optical beam induced current measurements at different light wavelengths. J. Appl. Phys., 66(7), 3060-3065, 1989.
View Article
[36] R. Mané, I. Ly, M. Wade, I., Diatta, M.S. Diouf, Y. Traoré, M. Ndiaye, S. Tamba and G. Sissoko. Minority Carrier Diffusion Coefficient D*(B, T): Study in Temperature on a Silicon Solar Cell under Magnetic Field. Energy and Power Engineering, 9, 1-10, 2017.
View Article
[37] M. Kunst, G. Muller, R. Schmidt and H. Wetzel. Surface and Volume Decay Processes in Semiconductors Studied by Contactless Transient Photoconductivity Measurements. Applied Physics, 46, 77-85, 1988.
View Article
[38] Y.L. Bocande, A. Correa, I. Gaye, M.L. Sow and G. Sissoko. Bulk and Surfaces Parameters Determination in High Efficiency Si Solar Cells. Proceedings of the World Renewable Energy Congress, Pergamon, Part III, Vol. 3, 1698-1700, 1994.
[39] G. Sissoko, C. Museruka, A. Corréa, I. Gaye and A. L. Ndiaye. Light spectral effect on recombination parameters of silicon solar cell. Renewable Energy, Vol 3, pp.1487-1490, 1996. Pergamon, 0960-1481
[40] H.Reinhard(1987). Equation aux dérivées partielles. Dunod Université, Paris.
[1] M. A. Green. Silicon Solar cells advanced principles & practice Printed by Bridge printer Pty. Ltd. 29-35 Dunning Avenue, Roseberry, Center for photovoltaic Devices and systems, March 1995; pp.29-35
[2] J.F. Wise. Vertical Junction Hardened Solar Cell. US Patent 3, 690-953, 1970.
[3] A. Gover and P. Stella. Vertical Multijunction Solar-Cell One-Dimensional Analysis. IEEE Transactions on Electron Devices, 1974, ED-21, 351-356. View Article
[4] M.M.S. Dede, M.L. Ba, M.A. Ba, M. Ndiaye, S. Gueye, E.H. Sow, I. Diatta, M.S. Diop, M. Wade, G. Sissoko. Back Surface Recombination Velocity Dependent of Absorption Coefficient as Applied to Determine Base Optimum Thickness of an n+/p/p+ Silicon Solar Cell. Energy and Power Engineering, 12, 445-458 https://www.scirp.org/journal/epe, (2020). View Article
[5] M.S. Diop, H.Y. Ba, N. Thiam, I. Diatta, Y. Traore, M.L. Ba, E.H. Sow, O. Mballo, G. Sissoko . Surface Recombination Concept as Applied to Determinate Silicon Solar Cell Base Optimum Thickness with Doping Level Effect. World Journal of Condensed Matter Physics, 9, pp.102-111, 2019. https://www.scirp.org/journal/wjcmp View Article
[6] G. Diop, H.Y. Ba, N. Thiam, Y. Traore, B. Dione, M.A. Ba, P. Diop, M.S. Diop, O. Mballo and G. Sissoko. Base thickness optimization of a vertical series junction silicon solar cell under magnetic field by the concept of back surface recombination velocity of minority carrier. ARPN Journal of Engineering and Applied Sciences Vol. 14, No. 23, pp.4078-4085, 2019.
[7] D. Faye, S. Gueye, M. Ndiaye, M.L. Ba, I. Diatta, Y. Traoré, M. Diop, G. Diop, A. Diao, Grégoire. S. Lamella silicon solar cell under both temperature and magnetic field: width optimum determination journal of electromagnetic analysis and applications, 2020, 12, 43-55 https://www.scirp.org/journal/jemaa View Article
[8] P.C. Dhanasekaran and B.S.V. Gopalam. Effect of Junction Depth on the Performance of a Diffused n+p Silicon Solar Cell. Solid State Electrons, 24, 1077-1080, 1981. https://doi.org/10.1016/0038-1101 View Article
[9] J.D. Arora, S.N. Singh and P.C. Mathur. Surface Recombination effects on the performance of n+-p step and diffused junction silicon solar cells. Solid State Electronics, 24(8), pp.739-747, 1981 View Article
[10] M.M. Ely , N. Thiam , M. Ndiaye , Y. Traore , R. Mane , E.H. Sow , O. Mballo , M.S. Diop , C.T. Sarr, I. Ly , G. Sissoko. Surface recombination velocity concept as applied to determinate back surface illuminated silicon solar cell base optimum thickness, under temperature and external magnetic field effects. Journal of Scientific and Engineering Research, 7(2):69-77, 2020
[11] N.M.M. Mohamed, O. Sow, S. Gueye, Y. Traore, I. Diatta, A. Thiam, M.A. Ba, R. Mane, I. Ly, G. Sissoko. Influence of Both Magnetic Field and Temperature on Silicon Solar Cell Base Optimum Thickness Determination. Journal of Modern Physics, 10, 1596-1605, 2020. https://www.scirp.org/journal/jmp View Article
[12]. M. Meusel, W. Benssch, T. Berdunde, R. Kern, V. Khorenko, W. Kostler, G. Laroche, T. Torunski, W. Zimmermann, G. Strobl, W. Guter, M Hermle, R. Hoheisel, G Siefer, E Welser, F. Dimroth, A. W. Bett, W. Geens, C. Baur, S. Taylor, G. Hey. Development and production of European III-V multijunction Solar cells. Proceeding of the 22nd European photovoltaic Solar Energy Conference, 2007. Pp. 16 - 51.
[13] G.E. Ayvazian, G.H. Kirakosyan and G.A. Minasyan. (2004). Characteristics of Solar Cells with Vertical p-n Junction. Proceedings of 19th European Photovoltaic Solar Energy Conference, Paris, 7-11 June 2004, 117-119.
[14] B. Ba, M. Kane, A. Fickou, G. Sissoko. Excess minority carrier densities and transient short circuit currents in polycrystalline silicon solar cells.Solar Energy Materials and Solar cells 31 pp. 33-49 0927-0248 /93/$ 06.00 © 1993 êlsevier Science Publishers B. V. View Article
[15] K. Joardar, R.C. Dondero and D.K. Schroda. Critical Analysis of the Small-Signal Voltage-Decay Technique for Minority-Carrier Lifetime Measurement in Solar Cells. Solid State Electronics, 32, pp.479-483, 1989. View Article
[16] P. Mialhe, G. Sissoko, F. Pelanchon, and J. M. Salagnon. Régimes transitoires des photopiles : durée de vie des porteurs et vitesse de recombinaison. J. Phys. III, France 2 pp. 2317-2331, 1992. View Article
[17] G.Sissoko, S. Sivoththanam, M. Rodot, P. Mialhe. Constant illumination-induced open circuit voltage decay (CIOCVD) method, as applied to high efficiency Si Solar cells for bulk and back surface characterization. 11th European Photovoltaic Solar Energy Conference and Exhibition (Montreux, Switzerland), 1992. Pp. 352-54.
[18] S. Mbodji, M. Zoungrana, I. Zerbo, B. Dieng and G. Sissoko. Modelling Study of Magnetic Field's Effects on Solar Cell's Transient Decay. World Journal of Condensed Matter Physics, 5, 284-293, 2015. doi: 10.4236/wjcmp.2015.54029. View Article
[19] S. Mbodji, I. Ly, A. Dioum, H. Ly Diallo, I.F. Barro, G. Sissoko. Equivalent electric circuit of a bifacial solar cell in transient state under magnetic field. Proceedings of the 21st European Photovoltaic Solar Energy Conference and Exhibition -Dresden, Germany, 2006, pp.447-450.
[20] Y. Betser, D. Ritter, G. Bahir, S. Cohen, and J. Sperling, "Measurement of the minority carrier mobility in the base of heterojunction bipolar transistors using a magnetotransport method", Appl. Phys. Lett., Vol. 67, No. 13, (1995) p 1883-1884. View Article
[21] S. Mbodji, A. S. Maiga, M. Dieng, A. Wereme, G. Sissoko. Removal charge technique applied to a bifacial solar cell under a constant magnetic field Global Journal of Pure and Applied Sciences, Vol.15, N°1, pp.125-132, 2009. View Article
[22] S. Madougou, F. Made, M.S. Boukary and G. Sissoko. I-V Characteristics for Bifacial Silicon Solar Cell Studied under a Magnetic Field. Advanced Materials Research, 18-19, 303-312, 2007.http://dx.doi.org/10.4028/www.scientific.net/AMR.18-19.303 View Article
[23] M. Fall, I., Gaye, D. Diarisso, G. Diop, K. Loum, N. Diop, K. Sy, M. Ndiaye and G. Sissoko. AC Back Surface Recombination Velocity in n+-p-p+ Silicon Solar Cell under Monochromatic Light and Temperature. Journal of Electromagnetic Analysis and Applications, 13, 67-81, 2021. doi: 10.4236/jemaa.2021.135005. View Article
[24] B.D.D. Sylla, I. Ly, O. Sow, B. Dione, Y. Traore, G. Sissoko. Junction Surface Recombination Concept as Applied to Silicon Solar Cell Maximum Power Point Determination Using Matlab/Simulink: Effect of Temperature. Journal of Modern Physics, 9, 172-188, 2018. http://www.scirp.org/journal/jmp View Article
[25] S. Mbodji, M. Zoungrana, I. Zerbo, B. Dieng, G. Sissoko. Modelling Study of Magnetic Field's Effects on Solar Cell's Transient Decay. World Journal of Condensed Matter Physics, 284-293, 2015. http://dx.doi.org/10.4236/wjcmp.2015.54029 View Article
[26] P. Diop, S. Gueye, G. Diop, D. Faye, I. Diatta, O.K. Dieng, O. Sow, M. Thiame, M. Wade and G. Sissoko. Influence de la température et du champ magnétique sur la décroissance transitoire de la densité des porteurs de charge dans une photopile au silicium a multi jonctions verticales connectées en parallèle et placée en circuit ouvert. International journal of advanced research. Int. J. Adv. Res. 10(08), 69-82, 2022. View Article
[27] C. Thiaw, M.L. Ba, M.A. Ba, G. Diop, I. Diatta, M. Ndiaye, G. Sissoko. n+-p-p+ Silicon Solar Cell Base Optimum Thickness Determination under Magnetic Field. Journal of Electromagnetic Analysis and Applications, 12, pp. 103-113, 2020. ISSN Online: 1942-0749 ISSN Print: 1942-0730: https://www.scirp.org/journal/paperabs.aspx?paperid=101717 View Article
[28] G. Diop, H.Y. Ba, N. Thiam, Y. Traore, B. Dione, M.A. Ba, P. Diop, M.S. Diop, O. Mballo and G. Sissoko. Base Thickness Optimization of a Vertical Series Junction Silicon Solar Cell under Magnetic Field by the Concept of Back Surface Recombination Velocity of Minority Carrier. ARPN Journal of Engineering and Applied Sciences, 14, 4078-4085, 2020.
[29] F.M. Ndiaye, M.L. Ba, M.A. Ba, G. Diop, I. Diatta, E.H. Sow, O. Mballo and G. Sissoko. Lamella Silicon Optimum Width Determination under Temperature. International Journal of Advanced Research, 8, 1409-1419, 2020. View Article
[30] N. Mohamed, O. Sow, S. Gueye, Y. Traore, I. Diatta, A. Thiam, M. Ba, R. Mane, I. Ly and G. Sissoko. Influence of Both Magnetic Field and Temperature on Silicon Solar Cell Base Optimum Thickness Determination. Journal of Modern Physics, 10, 1596-1605, 2019. doi: 10.4236/jmp.2019.1013105. View Article
[31] M.S. Dede, M.L. Lamine Ba, M.A. Ba, M. Ndiaye, S. Gueye, E.H. Sow, I. Diatta, M. Diop, M. Wade and G. Sissoko. Back Surface Recombination Velocity Dependent of Absorption Coefficient as Applied to Determine Base Optimum Thickness of an n+/p/p+ Silicon Solar Cell. Energy and Power Engineering, 12, 445-458, 2020. doi: 10.4236/epe.2020.127027. View Article
[32] B. Dione, O. Sow, M. Wade, I. Ly, S. Mbodji, G. Sissoko. Experimental Processus for Acquisition Automatic Features of I-V Properties and Temperature of the Solar Panel by Changing the Operating Point. Circuits and Systems, 7, 3984-4000, 2016 http://www.scirp.org/journal/cs ISSN Online: 2153-1293 ISSN Print: 2153-1285. View Article
[33] G. Sissoko and S. Mbodji. A Method to Determine the Solar Cell Resistances from Single I-V Characteristic Curve Considering the Junction Recombination Velocity (Sf). Int. J. Pure Appl. Sci. Technol., 6(2), pp.103-114, 2011.ISSN 2229 - 6107 Available online at View Article
[34] J. Furlan and S. Amon. Approximation of the Carrier Generation Rate in Illuminated Silicon. Solid-State Electronics, 28, 1241-1243, 1985. View Article
[35] Th. Flohr and R. Helbig. Determination of minority-carrier lifetime and Surface recombination velocity by optical beam induced current measurements at different light wavelengths. J. Appl. Phys., 66(7), 3060-3065, 1989. View Article
[36] R. Mané, I. Ly, M. Wade, I., Diatta, M.S. Diouf, Y. Traoré, M. Ndiaye, S. Tamba and G. Sissoko. Minority Carrier Diffusion Coefficient D*(B, T): Study in Temperature on a Silicon Solar Cell under Magnetic Field. Energy and Power Engineering, 9, 1-10, 2017. View Article
[37] M. Kunst, G. Muller, R. Schmidt and H. Wetzel. Surface and Volume Decay Processes in Semiconductors Studied by Contactless Transient Photoconductivity Measurements. Applied Physics, 46, 77-85, 1988. View Article
[38] Y.L. Bocande, A. Correa, I. Gaye, M.L. Sow and G. Sissoko. Bulk and Surfaces Parameters Determination in High Efficiency Si Solar Cells. Proceedings of the World Renewable Energy Congress, Pergamon, Part III, Vol. 3, 1698-1700, 1994.
[39] G. Sissoko, C. Museruka, A. Corréa, I. Gaye and A. L. Ndiaye. Light spectral effect on recombination parameters of silicon solar cell. Renewable Energy, Vol 3, pp.1487-1490, 1996. Pergamon, 0960-1481
[40] H.Reinhard(1987). Equation aux dérivées partielles. Dunod Université, Paris.

