Journal of Fluid Flow, Heat and Mass Transfer (JFFHMT)

ISSN: 2368-6111

Nomenclature

1. Introduction

Understanding the dynamics and thermodynamics of suspended inertial particles in turbulent flows, is crucial for various industrial and environmental applications. In many practical systems, e.g. combustors [1], or atmospheric clouds [2,3] particles (or bubbles or droplets) interact with the surrounding fluid, influencing the inter-phase transport of mass, momentum and heat. The best literature reviews of the recent theoretical, numerical and experimental efforts to report insightful information about this non-trivial physical problem can be found in [4-9].

Such a complex interplay gives rise to many complicated involved phenomena such as turbulence-induced thermophoresis, turbophoresis, clustering, preferential concentration, sweep-stick mechanisms, scattering, caustics, thermal caustics and preferential sampling that affect locally and non-locally fluid-particle thermal and mechanical interactions. Moreover, in the presence of turbulent mixing, multiscale interaction between mixing dynamics and turbulent flow influences the overall heat, mass and momentum transport in the flow domain. Although these phenomena and mechanisms exist in one- and two-way coupling regimes, in two-way coupled flows, particles ability to change the turbulence characteristics through their back-reaction adds another level of complexity to the problem. In a non-isothermal turbulent flow laden with inertial heavy particles, when particles can also carry enthalpy through the mixing layer, particles interact mechanically and thermally with the turbulent fields and mixing according to their inertia and thermal inertia. Meanwhile, due to the inherent challenges in precisely measuring the velocity and temperature of inertial particles, even with the use of advanced experimental techniques, Direct Numerical Simulation (DNS) is employed to enhance the understanding of the overall dynamics and thermodynamics. Owing to significant advancements in computational technology and the development of efficient algorithms in recent decades, DNS has emerged as a primary tool for investigating particle-laden turbulent flows across various fields, although it remains constrained to low and moderate Reynolds numbers.

The study of heat transfer within the two-way coupling regime has primarily focused on unbounded, statistically homogeneous turbulent flows, aiming to elucidate the impact of particle feedback on fluid temperature statistics and inter-scale heat transfer [10-13]. Nonetheless, the existing literature features limited research on this topic when the temperature field is inhomogeneous and statistically unsteady, as in the presence of a developing mixing layer.

Bec et. al. in [11] performed an analysis on fluid-particle thermal interaction in a homogeneous and isotropic turbulent flow, and reporting the role of particle temperature time derivative and fluid temperature gradients in inter-phase and inter-scale heat transfer. In that study, the thermal and dynamical behavior of inertial particles has been quantified in terms of particle inertia and thermal inertia and the ranges with maximum contribution has been identified. Carbone et. al. in [12] also performed a very comprehensive study on the multiscale thermal interaction taking into account the impact of particle collision and thermal feedback on the heat transfer in a homogeneous isotropic turbulent flow. Furthermore, we have recently investigated an anisothermal turbulent flow containing particles, where a thermal mixing layer develops in a quasi-self-similar manner between two homogeneous and isotropic homothermal regions. We analysed the dynamical and thermal effects of particle Stokes and thermal Stokes numbers, and the flow's Taylor microscale Reynolds number in both one-way and two-way coupling, considering both collisionless [14] and collisional regimes [15]. During our previous studies we have mainly attempted to explore the role of the major factors in overall heat transport between two homothermal regions, including particle inertia, thermal inertial, turbulence characteristics, the inter-particle collisions and particle feedback. In [14], while the particle dynamical and (τ_ϑ⁄τ_v=S t_ϑ⁄S t=4.43), we could quantify the particle contribution to the overall heat flux. In that work, since we neglected the effect of particle collisions, overall flow parameters reduced to the carrier flow turbulence characterized by Taylor microscale Reynolds number and particle inertia characterized by Stokes number as well as the particle thermal back-reaction. Note that due to the proportionality, particle thermal inertia can be seen through the variation of its inertia. The numerical experiments have enabled us to detect the different mechanisms and phenomena and quantify them in terms of flow parameters and report the range of inertia at which overall particle contribution is maximum. We reported how the multiscale heat transfer between particles and fluid, and turbulent mixing dynamics simultaneously affect the overall heat transfer. In this situation, on one hand, turbulence is advecting the temperature field and creating some temperature fronts, on the other hand, particles are interacting with both fluid turbulent fields and mixing at different scales in different particle inertia ranges. Moreover, we investigated the role of particle collisions in subsequent study [15], however; it has been found that the impact of the inter-particle collisions on the overall heat transfer is mild and it merely becomes more effective at higher particle inertia range. We also performed a comprehensive study on the effect of particle inertia and thermal inertia in such a case that these two parameters are not proportional and can vary independently in [16]. That investigation has been done only for a single Taylor microscale Reynolds number, Re_λ=56. We also proposed a novel decomposition of the velocity-temperature correlation in terms of particle velocity and temperature time derivative correlations, to better understand the different phenomena which are behind the variation of particle heat flux at various particle inertia and thermal inertial. The results regarding this novel decomposition obtained only for one-way coupling regime and to extend our knowledge and capture the effect of particle feedback, we preform a new set of simulations in two-way thermal coupling which has been reported in [17].

To complement the works related to the effective mechanisms in two-way coupling regime, specifically the crucial role of the particle thermal back-reaction in particle heat flux, we present new set of results for different Taylor microscale Reynolds numbers, ranging from 56 to 124 in this present work. In this study we aim to employ the proposed decomposition in [16] to analyze the effect of particle thermal feedback on heat flux at different Taylor microscale Reynolds numbers. We show how turbulent motion affects the way that particle thermally modulated fluid thermal fields and consequently changes the overall heat transfer at mixing layer. Accordingly, this study is more focused on the effect of particle back-reaction on the heat flux statistics at different Taylor Reynolds numbers, however; some statistics regarding the particle temperature time derivative in two-way coupling regime are also presented. The presented findings are useful to further studies in two-phase flows, especially when heat transfer is the core of the investigation.

2. Governing equations

The objective of this study is to investigate the heat transfer in the simplest thermally inhomogeneous turbulent flow, i.e. between two regions with uniform temperature, T₁ and T₂< T₁, in a particle-laden flow with homogeneous and isotropic velocity fluctuations. We adopt the point-particle Eulerian-Lagrangian direct numerical simulations. In the Eulerian frame, the Navier-Stokes equations are solved for the carrier flow, characterised by a divergence-free velocity field u(t,x), a pressure field p(t,x) , and a passively advected temperature field T(t,x), while individual particles are tracked along their Lagrangian paths. Under these assumptions, the dynamics of the fluid phase are governed by the incompressible Navier-Stokes equations, given by

(1)

(2)

(3)

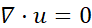
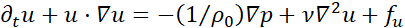
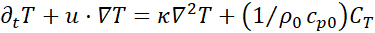
where ρ₀ denotes fluid density, c_p0 and ν represent the fluid isobaric specific heat capacity and kinematic viscosity, respectively; κ=λ_T⁄((ρ₀ c_p0 ) ) is the thermal diffusivity (λ_T is the thermal conductivity). Function f_u is an external body force introduced to maintain turbulent fluctuations in a statistically steady state, and C_T is the heat exchanged per unit time and unit mass with particles, representing the particle thermal feedback on the carrier flow.

In accordance with previous studies (e.g., [14-16]), we do not account for the force exerted by particles on the fluid. Instead, only the fluid temperature field is two-way coupled with the particles, while momentum exchange is restricted to the one-way coupling regime. This assumption leads to a dilute regime in our investigation. Anyway, it has been established that momentum feedback has a negligible thermal effect on fluid temperature statistics [12] even at higher concentrations.

The discrete phase is modeled as a set of monodisperse solid spheres of radius R, assumed to be smaller than the Kolmogorov lenghtscale η of the turbulent carrier flow. These material point particles have a density ρ_p much higher than the fluid density, and an isobaric specific heat capacity c_pp. In this situation the motion of the particle can be described by a simplified form of the equation proposed by Gatignol [18] and Maxey & Riley [19], in which the Stokes drag force is the dominant term in the force, and all other contributions are neglected. Some studies, such as [20,21], have thoroughly investigated the impact of the added-mass and other forces on particle dynamics in turbulent flows, which lead to a reduction of particle clustering for lighter particles, but produce negligible effects when the particle-to-fluid density ratio exceed 20. Thus, for the scope of this work, we focus on the simplified model valid for heavier particles as in our previous studies [14,17].

Analogous to the equation of motion of a rigid sphere in fluid, an equation for the particle temperature can be derived under the same hypothesis, so that the dynamics of each individual particle is governed by the following equations in the Lagrangian reference frame

(4)

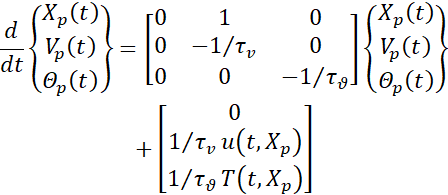
where X_p (t), V_p (t), and Θ_p (t) are position, velocity and temperature of the p-th particle, respectively, and define the dynamical state of the particle. In the following, a dot will be used to indicate the time derivative of particle variables, so that, for example, is the particle acceleration. Here τ_v and τ_ϑ are the momentum and thermal relaxation times, given by

(5)

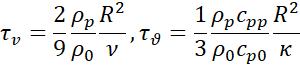
Any direct particle-particle interaction, including collisions, is excluded. Collisions, which become more frequent as particle density increases, have a minor effect on the heat flow in this configuration, as shown in [15], producing a mild reduction of the particle contribution which becomes appreciable only for large inertia. The only interaction between particles is thermal and mediated by the carrier fluid: particle thermal feedback modifies the carrier flow temperature and this affects other particles. The particle thermal feedback per unit time and unit volume is given by

(5)

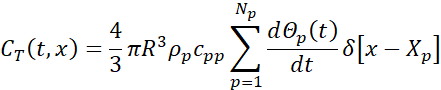
where N_p is the total number of spherical inertial particles and δ(⋅) is the Dirac delta function.

3. Flow setup and numerical method

We use the same computational setup of [14], so that the governing equations are solved in a parallelepiped computational domain with dimensions L₁=L₂ and L₃=2L₁ along the x₁, x₂, and x₃ directions. The temperature distribution is initialized by setting the temperature equal to T₁ in the half-domain where x₃< L₃⁄2 and equal to T₂ in the half-domain where x₃< L₃⁄2. Periodic boundary conditions are imposed to the velocity field on all faces of the computational domain, while the temperature field, which is intrinsically non periodic, is decomposed into a mean linear steady part and a fluctuating part, to which periodic boundary conditions can be applied, as described in detail in [14]. Moreover, for the sake of consistency with physics of the two-phase flow, periodicity is applied also to particles, so that any particles that may exit the computational domain is reintroduced on the opposite side with the same velocity and fluctuating part of its temperature.

The governing equations are solved in dimensionless form. They are non-dimensionalized by using L₁=L₁⁄2 π as reference length, a reference velocity which is deduced from the imposed kinetic energy dissipation rate ε, and the temperature difference T₁-T₂ as reference temperature [14]. The flow is forced on a single length-scale L₁=L₁⁄2 π, and the linear deterministic forcing, which allows to control both the forced length-scale and the energy injection rate, is used, as in [12,14,16]. To make the results physically significant, the Taylor-microscale is used as the reference length in the definition of the Reynolds number instead of the (arbitrary) domain size L₁=L₁⁄2 π

In the dimensionless form, the flow is governed by the Reynolds number Re_λ=u'λ⁄ν, the Prandtl number Pr=ν⁄κ, and the particle thermal mass fraction or particle-to-fluid heat capacity ratio φ_ϑ=φ (ρ_p c_pp )⁄(ρ₀ c_p0 ), where φ is the particle volume fraction. In dimensionless form, particle dynamics is determined by the ratio between their relaxation times and the flow timescales. To characterize the particle dynamics in terms of local fluctuations of fluid state, the Kolmogorov timescale τ_η=(ν⁄ε)^1⁄2 is used instead of the large-scale time used in the adimensionalization. Thus, the Stokes number St=τ_v⁄τ_η and the thermal Stokes number St_ϑ=τ_ϑ⁄τ_η are used to describe the particle dynamical and thermal behavior. A pseudospectral method, fully dealiased by using the 3/2-rule, was employed to discretize the spatial domain of the fluid phase equations (1-3). The forcing function f_u was defined in Fourier space as

(7)

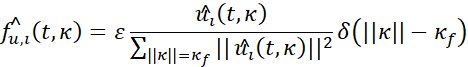
where ε denotes the energy injection rate, equal to the kinetic energy dissipation in statistically steady conditions, κ is the three-dimensional wavenumber, and κ_f is the forced wavenumber. Interpolation of fluid velocity and temperature at particle positions, necessary to determine u(t,X_p ) and T(t,X_p ) in equation (4), and the computation of the particle thermal feedback (6) were carried out using a recent numerical method [22,23] based on inverse and forward non-uniform fast Fourier transforms with a fourth-order B-spline basis. Integration in time was performed for both the carrier flow equations (2-3) and the particle equations (4) using a second order exponential integrator. More details about the numerical method and flow setup can be found in [14] and [22].

All the results we present in the following section come from simulations carried out using 256²×512 Fourier modes (after dealiasing using the 3/2 rule, i.e. 384²×768 grid points in physical space) in the 2π×2π×4π domain in dimensionless form, so that the resolution is the same in every direction. This grid resolution ensures that κ_max η>2 (κ_max η is the maximal wavenumber), so that all turbulent scales up to the Kolmogorov microscale are resolved, and the interpolation does not introduce spurious fluctuations of particle acceleration. For all simulations particle volume fraction is kept constant and equal to φ=4×10^-4 and a particle to fluid density ratio ρ_p⁄ρ₀=10³. The Taylor miscroscale Reynolds number Re_λ varies from 56 to 124. Particle size and number are determined from the volume fraction and density ratio by the Stokes number. We consider the Stokes and thermal Stokes number as independent parameters, so that the particle specific heat is adjusted accordingly. The thermal Stokes number ranges from 0.1 to 10 and the Stokes number from 0.2 to 5. All relevant flow parameters are listed in table 1. The initial conditions for the simulations involve a randomly initialized velocity field, which is evolved in time until statistical stationarity is reached, then it is randomly seeded by particles, with a uniform distribution.

Table 1. Dimensionless flow parameters.

Simulation		I	II	III
Taylor microscale Reynolds number	Reλ	56	86	124
Taylor microscale	λ	0.226	0.29	0.35
Integral length scale	l	0.40	0.74	0.94
Root mean square of velocity fluctuations	u'	0.59	0.71	0.85
Forced wavenumber	κf	5	√6	√3
Prandtl number	pr	0.71	0.71	0.71
mean turbulent kinetic energy dissipation rate	ε	0.25	0.25	0.25
Kolmogorov length scale	η	0.0153	0.0153	0.0153
Kolmogorov time scale	τη	0.098	0.098	0.098
Particle volume fraction	φ	4 × 10-4
Density ratio	ρp⁄ρ0	103
Stokes number	St	0.2 ; 0.7 ; 0.8 ; 0.9 ; 1 ; 1.2 ; 1.5 ; 2 ; 2.5 ; 3.5 ; 4 ; 5
Thermal Stokes number	Stϑ	0.1 ; 0.2 ; 0.3 ; 0.5 ; 0.7 ; 1 ; 1.2 ; 1.5 ; 2 ; 3 ; 4 ; 5 ; 6 ; 7 ; 8 ; 9 ; 10

4. Correlation decomposition

The thermal discontinuity which initially separates the two homothermal regions is spread by the turbulent velocity field creating an interaction layer characterized by the presence of a mean temperature gradient and, a consequence, a heat flux between the two regions. This layer grows in time as the process occurs [14]. Therefore, the most important quantity is the heat flux across this layer, which is due to both conduction, turbulent fluctuations and the motion of particles. Given the statistical inhomogeneity and unsteadiness of the temperature, in the following we consider conditional averages at a given time and position x₃ along the inhomogeneous direction, i.e., we define, for any function f of the state of the particle,

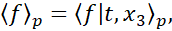
where ⟨⋅⟩_p is the statistical average and we define the fluctuation of f as f'=f-⟨f⟩_p. The heat flux across the inhomogeneous layer, i.e. in direction x, is

(8)

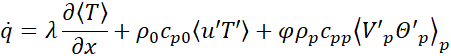
where the last term is the contribution of particles motions, which is the focus of this work [14]. Following [16], we can express the average heat flux in terms of the time derivatives of particle velocity (i.e., the particle acceleration) and temperature. By subtracting from (4) its conditional average, the particle temperature and velocity fluctuations can be expressed as

(9)

(10)

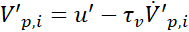
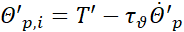
where fluid velocity and temperature are to be computed at particle position. Since the mean velocity is zero, in the following we will skip the apex from all moments that are second order or higher to keep notations simple. By cross multiplying equations (9) and (10) and taking the conditioned statistical average, we obtain the following expression of the particle velocity-temperature correlation [16]

(11)

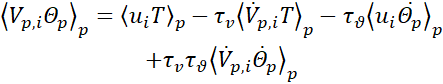
which expresses the particle contribution to the convective heat flux. This correlation can be conveniently divided by the fluid velocity-temperature correlation to obtain

(12)

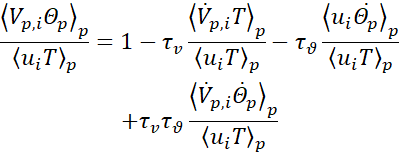
This ratio relates, apart for a constant coefficient (the particle to fluid heat capacity), the particle and fluid contributions to the Nusselt number (see [14]). In this way, we have decomposed the particle contribution to the heat flux in terms of the correlations between the particle derivatives and between them and the fluid velocity and temperature fluctuations. The particle derivatives account for the instantaneous heat exchanges between the two phases and strongly depend on both relaxation and thermal relaxation times, which also explicitly appear as coefficients in the decomposition.

Decomposition (11) has been used in [16] only in the one-way coupling regime and in [17] in two-way coupling regime at a single Taylor microscale Reynolds number equal to 56 and for a wide range of Stokes and thermal Stokes numbers. Here, we aim to elucidate the role of particle feedback by analysing the flow at different Taylor Reynolds numbers.

Since x₃, the direction normal to the initial interface and parallel to the mean gradient, is the only non homogeneous transport direction, the index will be omitted from all velocity and acceleration components. To comprehend how particle feedback modifies the fluid temperature fluctuations and, consequently, the fields experienced by the particles, we employ the proposed decomposition (11) and some of its terms in two-way coupling, comparing them with the corresponding terms in the one-way coupling at different Reynolds and Stokes/thermal Stokes numbers. As in [14], all data will be presented in the central sublayer of the interaction layer, where the mean temperature gradient is largest. The observed self-similarity allows to extend the comparison to the whole layer.

5. Results

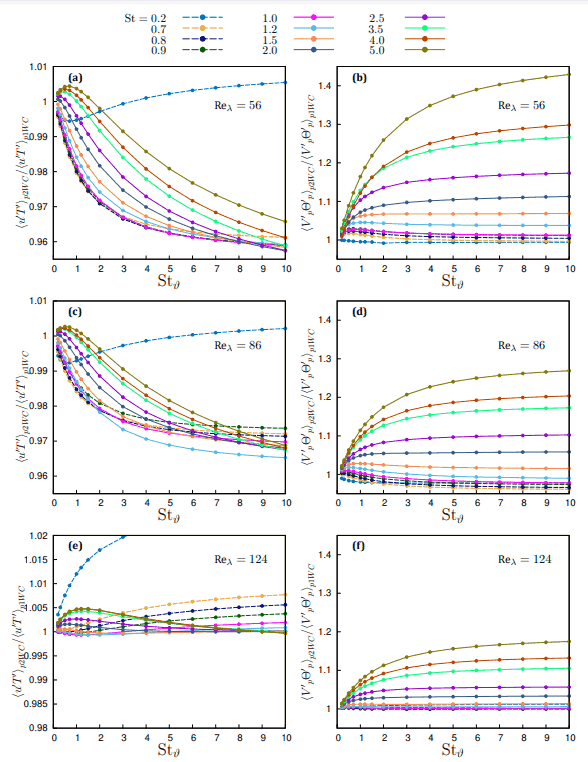
First, we present the overall effect of particle feedback on the heat transport by comparing the fluid and particle velocity-temperature correlation in the one- and two-way coupling. Figure 1, panels (a), (c) and (e) illustrate the ratio between fluid velocity-temperature correlation in one- and two-way coupling while figure 1, panels (b), (d) and (f) show the ratio between particle velocity-temperature correlations in one- and two-way coupling at Taylor Reynolds number Re_λ=56, Re_λ=86 and Re_λ=124 respectively. As observed in homogeneous flows, particles tend to accumulate in regions with high temperature gradients [11], and their thermal back-reaction tends to reduce fluid temperature gradients [12]. Consequently, particle feedback decreases the fluid velocity-temperature correlation, an effect that intensifies with increased particle thermal inertia, i.e., at higher thermal Stokes numbers. Particles with very low inertia cannot cross temperature fronts, limiting their modulation effect, regardless of their thermal inertia. Intermediate inertia particles are more effective in reducing the fluid velocity-temperature correlation, since they can experience different temperature gradients regions, interact with larger turbulence scales. This effect becomes more pronounced when the Stokes number is of order one due to the intense particle clustering at temperature fronts. As thermal inertia increases, the reduction mechanism is amplified, allowing particles to smooth temperature fronts and alter small-scale fluid temperature field. However, for St_ϑ≫1, the relative reduction seems to be independent of St for intermediate inertia particles, quickly saturating.

Larger inertia particles behave differently, initially increasing the correlation if their thermal Stokes number is less than one, but reducing it as thermal inertia increases. Thus, they can enhance turbulent convective heat transfer at lower thermal inertia but hinder it at higher thermal inertia due to their longer relaxation time, which makes the damping effect due to the thermal disequilibrium prevail. Thus the maximum effect is seen at intermediate thermal inertia, where particle benefit from clustering. Two-way coupling always increases the particle velocity-temperature correlation, figure 1, panels (b), (d) and (f), as seen in [14,16].

For small Stokes numbers, the effect is negligible and almost independent of thermal Stokes number, becoming significant when St becomes of order one. Feedback reduces the particle-to-fluid temperature difference, slowing particle temperature variation and enabling particles to carry enthalpy over longer distances. Higher thermal inertia increases the particle velocity-temperature correlation by allowing particles to interact locally and non-locally with different turbulent eddies and, by crossing temperature fronts, by smooth fluid temperature fluctuation and decorrelating them from velocity fluctuations. The overall heat flux depends on the particle thermal mass fraction φ_ϑ which is proportional to the particle-to-fluid heat capacity ratio. At the simulated volume fraction, 4×10^-4, the particle phase has a higher heat capacity than the fluid, φ_ϑ≃1.664 increasing the total heat flux even when they damp the convective heat flux of the carrier fluid. This pattern persists across different Taylor microscale Reynolds numbers, though the magnitude of particle contribution to the heat flux decreases with increasing Re_λ. Indeed, the maximum particle heat flux occurs at the lowest simulated Reynolds number, consistent with previous observations [14,17]. The timescale for fluid temperature modulation by fluid-particle thermal interaction, τ_T∼τ_ϑ⁄φ_ϑ [13,14], is crucial. Since mixing dynamics is governed by large-scale turbulence, characterized by the large-eddy turnover time τ, the ratio τ_T⁄τ∼φ_ϑ^-1 St_ϑ Re_λ^-1 reveals the interplay between thermal inertia and large-scale turbulence. Larger particle thermal inertia requires more time for thermal field modulation at a given Reynolds number, as confirmed by figure 1, panels (a), (c), and (e). Increased Reynolds numbers result in faster mixing, reducing the effectiveness of particle thermal modulation.

Figure 2, panels (a), (c) and (e) show that the variance of particle temperature time derivative is always reduced by thermal feedback across all simulated particle inertia, thermal inertia and Reynolds numbers. This reduction is more pronounced at higher thermal Stokes numbers and intermediate particle inertia, as particles in these parameter ranges can interact with intermediate fluid structures and modulate them. Higher thermal inertia at the same inertia reduces the effectiveness of this feedback mechanism. Lower inertia, as in the St=0.2 case, have limited impact, regardless of their thermal inertia, because they cannot affect the formation of temperature fronts.

Large-scale turbulence seems to have a minor influence on the mechanism through which particle temperature time derivative is decreased by thermal feedback, except at the highest Reynolds number, Re_λ=124 and for the smallest inertia particles, St=0.2. Variance in particle temperature time derivative increases with particle inertia but decreases with increasing thermal inertia, a universal pattern across all simulated Reynolds numbers. Higher thermal inertia reduces inter-phase heat transfer, with particles retaining their temperature and filtering out small-scale fluctuations. This behavior is due to the role of particle thermal inertia, since as particle thermal inertia increases the inter-phase heat transfer reduces. Two mechanisms are responsible for this reduction, first, particles with higher thermal inertia tend to keep their temperature and they also filter out the small scale temperature fluctuations. Secondly, they respond only to the larger scale of thermal field and by modulating it with their back-reactions.

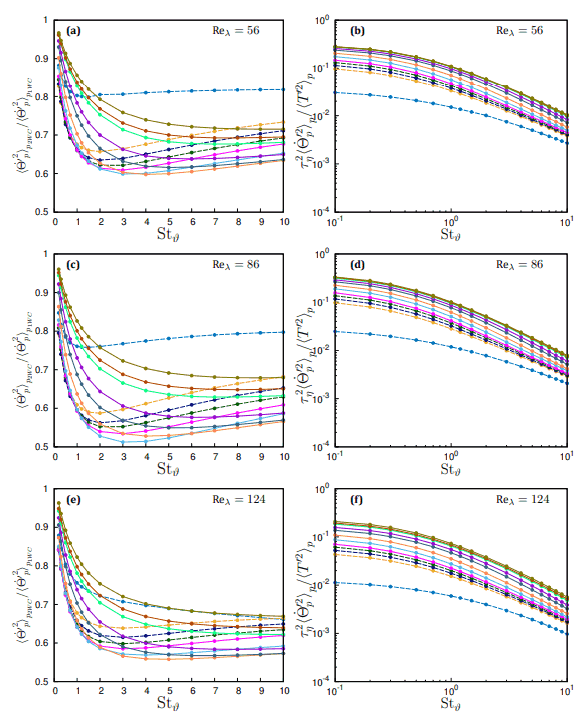
In homogeneous turbulence, the presence of a smooth temperature field leads to a finite limit of the variance of for small thermal Stokes numbers [12]. Conversely, in the opposite limit, with very large thermal inertia, the thermal acceleration integral tends to be dominated by uncorrelated temperature increments, The data in figure 2, panels (b), (d) and (f) illustrate a low thermal inertia finite limit at all simulated Stokes numbers, suggesting a smooth temperature field. This is consistent with the fact that, in the limit of vanishing St_ϑ there is no difference between one- and two-way thermal coupling, Figure 2, panels (b), (d) and (f), and the one-way coupled simulations show a smooth behavior [15]. Meanwhile, the behaviour in the self-similar stage in the presence of high thermal inertia demonstrates the presence of well-mixed regions within the thermal mixing layer core, even if the asymptotic scaling of homogeneous turbulence is not reached in the range of simulated thermal Stokes numbers. As observed in [15], this could be due to the existence of a strong mean temperature gradient which dominates large-scales temperature variations, the only one which can be felt by very high inertia particles. However, we can see a small variation in magnitude of this quantity for different Re_λ and the difference is more pronounced for lower inertia particles. At the smallest simulated Stokes number, i.e. St=0.2 the variance of particle temperature time derivative reduces with Re_λ the most. We can also see this reduction also for intermediate and high Stokes numbers as Re_λ increases, but at a smaller range with respect to the smallest Stokes number, 0.2.

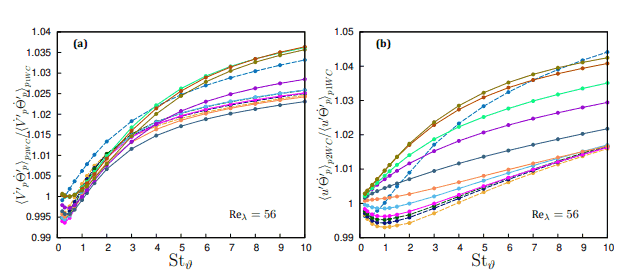
How the particle acceleration and temperature time derivative influence the velocity-temperature correlation, which gives the heat flux, can be seen from the decomposition introduced in section 4. Analyzing the three terms on the right-hand side of equation (11), we note all terms are negative, with the first two building the correlation while the third one dampens it [14]. A positive velocity fluctuation produces a positive temperature fluctuation, leading to a negative temperature time derivative because the particle is most often moving into a colder zone, thus being cooled by the surrounding fluid. Correlations involving particle acceleration are less intuitive, even if higher acceleration are expected for particles which are in the higher strain zones [24]. However, in [16], for one-way coupling at Re_λ=56, we observed that this correlation is negative for all St and St_ϑ Furthermore, figure 3 (a) indicates the same sign in two-way coupling at Re_λ=56 for all ranges of particle inertia and thermal inertia, as the ratio remains positive. Conversely, the correlation was found to be negative in one-way coupling atRe_λ=56 in [16]. Figure 3 (b) confirms the same sign in two-way coupling regime. Thus, we can conclude that particle thermal feedback does not change the sign associated to the particle acceleration and temperature time derivative used in the decomposition analysis. The acceleration-temperature time derivative correlation (last term of equation (11)) increases with St_ϑ contributing to a reduction in particle heat flux, appreciable at large Stokes and thermal Stokes numbers. For any given Stokes number, thermal feedback increases the modulus of the correlation between particle velocity and temperature time derivative.

Figure 3(a) illustrates the correlation between acceleration and the time derivative of temperature, which is the last term of equation (11) This correlation increases with St_ϑ and exhibits a minor dependence on St. It contributes to the reduction of particle heat flux, an effect which becomes significant only for large Stokes and thermal Stokes numbers due to the multiplication by the product of the relaxation times, τ_v τ_ϑ. This term only becomes relevant and potentially dominant for very large values of St and St_ϑ. However, for any given Stokes number (i.e., for any fixed τ_v), it does not dominate the other terms, at least up to St=5. A reduction in heat flux can only be observed at high St if the ratio τ_ϑ⁄τ_v =S t_ϑ⁄S t is kept fixed. This indicates that the impact of the acceleration-temperature time derivative correlation in reducing particle heat flux is contingent on the values of St and St_ϑ. For most practical applications, this term does not overshadow the other terms unless the Stokes and thermal Stokes numbers are exceptionally large. Additionally, maintaining a fixed ratio of τ_ϑ to τ_v is crucial for observing a notable reduction in heat flux at high Stokes numbers. This finding offers a potential explanation for the reductions in heat flux observed in specific flow configurations, as documented in certain flow configurations [25].

Since particles are momentum one-way coupled only, fluid velocity and particle accelerations are independent of any thermal effects, with thermal feedback affecting only T. This implies that two-way coupling increases the sum of the last two terms in equation (11), overcoming the observed reduction in . Since their sum is equal to , thermal feedback tends to increase the modulus of the correlation between particle velocity and temperature time derivative.

6. Discussion and conclusion

We have studied the effects of inertia and thermal inertia on the velocity-temperature correlations, which produce the turbulent heat flux, in a simple inhomogeneous particle-laden turbulent flow, focusing on the effect of particle thermal feedback. Low inertia particles (St≪1) give a minimal contribution, because they follow local fluid motion and interact with small-scale turbulence only. When they have also low thermal inertia (St_ϑ≪1) they transfer heat only over short distances because they quickly reach thermal equilibrium with the surrounding fluid. When they have high thermal inertia (St_ϑ≫1) they smooth the fluid temperature field by storing and releasing heat over longer periods. Despite this, their small inertia prevents them from crossing different temperature fronts, resulting in a modest contribution to overall heat transfer and a limited modulating effect. High inertia particles (St≫1), whether with low or high thermal inertia, significantly enhance the overall heat transfer by moving through different temperature fronts, homogenising sharp zones, and increasing thermal mixing efficiency. Their ability to cross and disrupt temperature fronts, whenever they have a rapid or slow response to fluid temperature changes, allows for effective homogenisation of fluid temperature gradients, modification of large-scale thermal fields, and increased overall heat flux, promoting uniform temperature distribution and redistributing thermal energy along their trajectories. Intermediate inertia particles (St∼1) and thermal inertia (St_ϑ∼1) balance both effects, enhancing their contribution to the heat transfer by matching timescales with turbulent flows and interacting with intermediate-scale turbulence. They efficiently homogenise temperature fronts and can cross different fronts, experiencing various regions of the flow domain and locally exchanging heat with the fluid. However, clustering makes also their thermal feedback more effective in reducing fluid temperature fluctuations, reducing the fluid velocity-temperature correlation. The decomposition of the correlation in terms of particle acceleration and temperature derivative has been used to underscore their significant role in modulating particle heat flux through the thermal feedback. Although particle acceleration is influenced by large scale motions of the turbulent flow, the variance of the particle temperature time derivative behaves almost independently of Re_λ. The turbulent convective term is indirectly affected by particle inertia and thermal inertia through the thermal feedback effect on fluid temperature field and can either increase or reduce the particle velocity-temperature correlation. The findings indicate that effectiveness of particle modulation on turbulent convective terms diminishes as the Taylor Reynolds number increases. Numerical results further show that the first two particle correlation terms in the decomposition contribute to the heat flux, whereas the last term, i.e. the acceleration-temperature time derivative correlation, reduces it, in both one- and two-way coupling regimes. However, the overall contribution results from the interplay of all terms across different inertia and thermal inertia ranges. It has been observed that the overall amplification of particle heat flux due to particle thermal feedback occurs at larger St and St_ϑfor any Re_λ. Moreover, the large-scale motions of turbulence, affecting all terms, generally lead to reduction in particle heat flux through particle thermal back-reaction as Re_λ increases. This phenomenon arises from the faster dynamics of the carrier flow, which makes the particle feedback less effective and hinders particle thermal interaction within the mixing layer, as particles in accelerated flows have less time to modulate the fluid temperature field. Additionally, at increased Re_λ, the particle acceleration also increases, leading to an enhanced , which is responsible for the reduction of . Consequently, as predicted by the decomposition, we have observed that the ratio between particle velocity-temperature correlation in one- and two-way coupling is maximum at the lowest Taylor microscale Reynolds number. Furthermore, at the highest ranges of particle inertia and thermal inertia for any Taylor Reynolds number, the time derivative of particle temperature diminishes. Our comprehensive observations using the decomposition conclude that the amplification of particle heat flux due to the thermal feedback is achieved at the highest inertia and thermal inertia and the lowest Taylor Reynolds number as thermal modulation operates most effectively under these conditions.

The proposed decomposition aids in understanding the intricate fluid-particle thermal interactions, by examining how different terms contribute to the particle heat flux and how these contributions vary with flow parameters. This decomposition can allow for a more thorough analysis, prediction and control thermal behaviors in such a complex flow in practical applications.

Acknowledgements

The authors acknowledge the CINECA award IsCb6_TCPLF, HP10CN9N4N, under the ISCRA initiative, for the availability of high performance computing resources and support. Additional computational resources provided by hpc@polito (http://www.hpc.polito.it) are also gratefully acknowledged.

References