Journal of Fluid Flow, Heat and Mass Transfer (JFFHMT)

ISSN: 2368-6111

Optimization and Sensitivity Analysis of Natural Convective Heat Transfer of Nanofluids inside a Quarter-Circular Enclosure Using Response Surface Methodology

Sajia S. Keya¹, M.S. Alam¹, M.N. Huda¹, M.M. Rahman^2,*

¹Department of Mathematics, Jagannath University
Dhaka-1100, Bangladesh
²Department of Mathematics, College of Science, Sultan Qaboos University
Muscat, Oman
*Corresponding author: mansur@squ.edu.om

Abstract - This research uses the non-homogeneous dynamic mathematical model to present a numerical study on nanofluids' convective heat transfer flow in a quarter-circular-shaped enclosure. The circular arc of the enclosure is continually maintained at a low temperature, while the bottom wall is hot and the vertical wall is adiabatic. An angled periodic magnetic field permeates the cavity and is affected by gravity. The Galerkin finite element approach solves the governing complex nonlinear equations to comprehend nanofluids' flow dynamics, temperature distribution, and concentration levels. The impact of the input model parameters on the output response function (mean Nu) is determined through response surface methodology. The results indicate that the external magnetic field and its orientation significantly impact the flow pattern of nanofluid. The Nusselt number substantially increases with the higher nanoparticle volume fraction, magnetic field period, inclination angle, and a higher Rayleigh number. The mean Nu value of the Fe₃O₄-kerosene nanofluid is considerably higher than that of the other five nanofluids analyzed in this study. Significantly, the Co-kerosene nanofluid demonstrates a superior average Nu to the other five nanofluid kinds. Specifically, the heat transfer augmentation rates for kerosene-based nanofluids, namely, Fe₃O₄, ZnO, and Co, are 1278.1%, 1001.8%, and 1258.7%, respectively, when compared to the corresponding base fluids, for a nanoparticle volume fraction of 5%. Conversely, the heat transfer rates are 449.4%, 470.2%, and 492.6% for H₂O-based similar nanofluids. These remarkable findings encourage the practical use of the studied nanofluids.

Keywords: Heat transfer; nanofluid; response surface methodology; periodic magnetic field.

© Copyright 2024 Authors - This is an Open Access article published under the Creative Commons Attribution License terms Creative Commons Attribution License terms. Unrestricted use, distribution, and reproduction in any medium are permitted, Pr ovided the original work is Pr operly cited.

Date Received: 2024-04-19
Date Revised: 2024-07-02
Date Accepted: 2024-07-30
Date Published: 2024-08-08

1. Introduction

The convection (CV) mode of heat transmission is a widely observed phenomenon used for heat transport and is crucial in engineering systems, as it facilitates heat transfer (HTR). This phenomenon is particularly significant in numerous applications. Natural convective HTR is widely used in engineering and industrial fields such as geophysics, biology, electronic cooling, solar, and nuclear energy [1-5]. Free convection processes have numerous advantages, including minimal noise and cost-effectiveness. Past studies have primarily focused on cooling modules incorporating cavity-shaped sections using a natural convection method. Akinsete and Coleman [6] present a survey of the features of free convective HTR in a triangle vicinity with different aspect ratios. In their study, Karatas and Derbentli [7] examined the convective phenomenon in a quadrilateral vicinity, specifically focusing on how the aspect ratio adjustment affects the average Nu. In their study, Gawas and Patil [8] inspected the phenomenon of free convective HTR within a square vicinity. They found that the Ra influenced the flow and thermal distribution, particularly at large values. The experimental tests conducted by Njoroge et al. [9] and Chen et al. [10] demonstrated poor HTR coefficients in their investigations.

Nanofluids (consisting of nanoparticles evenly distributed in base fluids) are an innovative category of HTR fluids utilized in nanotechnology, providing significant benefits compared to traditional HTR fluids. As Maxwell [11] proposed over a century ago, the most advantageous characteristic of nanofluids is their superior thermal conductivity (THC). Therefore, nanofluids (NAFs) are the future working fluids in contemporary HTR technologies. The primary characteristic of NAFs that signifies their potential for heat transmission is their THC. The study conducted by Masuda et al. [12] has discovered a remarkable outcome regarding the THC of suspensions by the dispersion of ultra-fine particles. The researchers found that the THC of water had a 32% rise, inserting 0.04 vol% of Al₂O₃ nanoparticles measuring 13nm in size into the base fluid. This discovery was subsequently examined by other researchers, including Choi [13] and Eastman et al. [14]. Uddin and Rahman [15] established a nonhomogeneous dynamic model of NAFs to overcome the constraints of current one- and two-component HTR models. They numerically examined the HTR mechanism inside a semi-circular form enclosure filled with various NAFs using a nonhomogeneous dynamic model. The shape of the enclosure is crucial for both design objectives and engineering applications.

Turcotte and Lyons [16] created a periodic MAF to study fluid flow and discovered that viscosity effects are restricted when the contact factor is significant. The findings of Geridonmez and Oztop [17] indicate that velocity and temperature decrease proportionally with the increased Lorentz force. A study by Dahmani et al. [18] discovered that a non-uniform periodic current-carrying wire in an enclosure can significantly accelerate the HTR of ferrofluid. The researchers found that the periodic wire increased the Nusselt number by up to 20% compared to a straight wire. Alam et al. [19] conducted a mathematical investigation considering transient convective flow in a square cavity subject to a slanted periodic MAF. Their findings indicate that the MAF's leaning angle significantly influences the walls' HTR properties. Huda et al. [20] investigated the impacts of an angled MAF on the Cu-H₂O nanofluid flow inside a square cavity. As the incident period increases consistently, the model parameters (Ra, particle volume fraction, sloping angle) cause a progressive increase in the thermal distribution rate, as indicated by the outputs. They also found that the sinusoidal thermal pattern on the left heated barrier produces the highest average Nu compared to other thermal settings.

Researchers and engineers frequently employ sensitivity (SNY) analysis in conjunction with the response surface technique to optimize designs and operating conditions. This method offers an effective framework for evaluating the influence of numerous critical factors on the system's performance [21-23]. The application of response surface technology has led to the optimization of the thermal efficiency of various heat transfer devices, resulting in the development of more efficient cooling and heat exchanger systems. These practical implications underscore the significance of our research in the field of heat transfer and system optimization.

Furthermore, the investigations above have shown that none of the previous studies considered the influence of an angled periodic MAF on various NAFs contained in a quarter circular enclosure, utilizing the response surface methodology. This study aims to create a unified numerical model that can explore the natural convection thermal transmission of various NAFs containing a quarter circular enclosure under the impact of a sinusoidal MAF. The numerical outcomes from the GFE process are demonstrated via graphs and tables, showing the changes in different components. The correlation equation is derived using the response (RES) surface tactic, employing the input data for the average Nu. The RES surfaces and contours derived from the RES surface methodology illustrate the interactions of the relevant components on the HTR rate. The analysis also examines how sensitive the output response is to the input parameters. The findings could be valuable in assessing the HTR appearances of thermal exchangers, solar collectors, and electronic devices.

2. Physical Modelling

The current problem involves the application of an angled periodic MAF to a quarter circular cavity filled with Fe₃O₄-kerosene nanofluid (see, Fig. 1). The magnetic field affects the entire flow domain. The properties of a periodic MAF include its period , which refers to the time it takes for the field to complete one cycle, and its amplitude B₀, which represents the maximum strength or intensity of the field. In our study, the bottom wall is regarded as being heated and is described as T=T_h. The vertical wall is considered adiabatic, meaning no heat transmission occurs over this limit. The temperature of the circular boundary of the cavity is T=T_c .

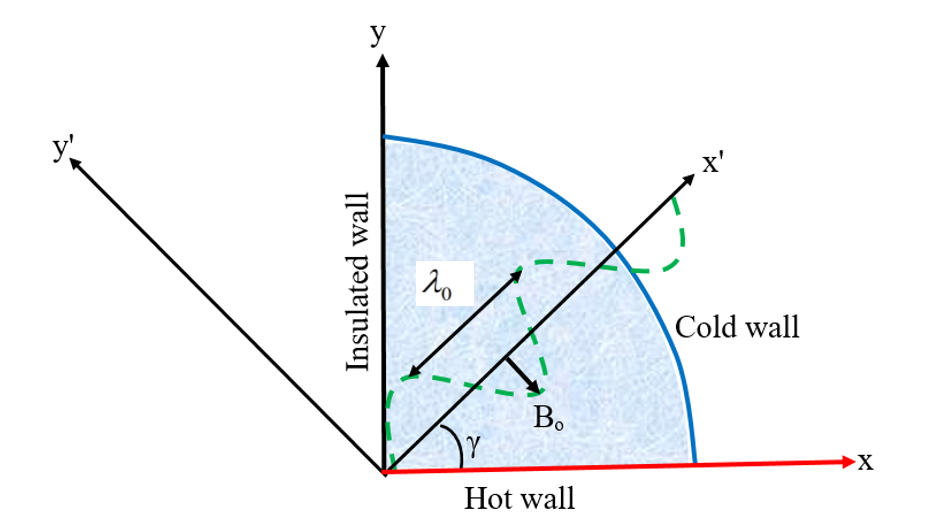
At first, the nanofluid concentration is considered to be at a low level ofC_C. However, for t> 0, C_h is expected to be uniformly distributed throughout the entire domain so that C_h>C_c . Our study incorporates Brownian diffusion and gravity factors, excluding chemical reaction and thermal radiation. The BAF and solid NAPs are in thermal equilibrium. An inclined periodic applied MAF permeates the cavity, with the direction of the MAF forming an angle with the positive x-axis. The inclined periodic MAF is described by

(1)

The transfer system provided enables transportation of the mentioned x and y-coordinates as:

(2)

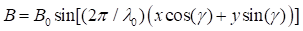
3. Mathematical modelling

3.1. Conservation equations for nanofluids

To better understand the density and stability of NAPs within base fluids, we included the nanofluid concentration equation in traditional mathematical models that focus on a single component. The 2D nanofluid flow is described by a set of dimensionless model equations inside the specified geometry domain [15, 24-25].

Continuity equation

(3)

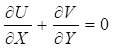
Momentum equation in X-direction

(4)

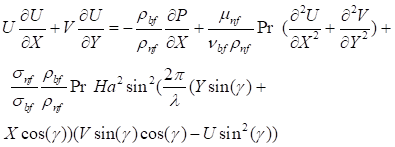
Momentum equation in Y-direction

(5)

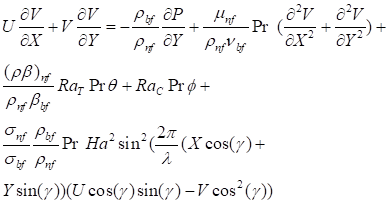
Energy equation

(6)

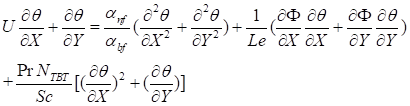
Concentration equation

(7)

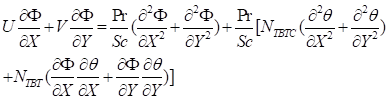
where , , , , , , ,

,

,,,

,

, .

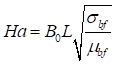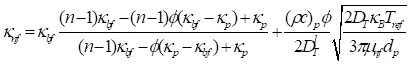The average Nusselt number is defined by

(8)

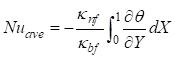
3.2. Non-dimensional boundary conditions

The initial and BACs for the current problem can be expressed in a dimensionless manner as follows:

On the horizontal base barrier:       (9a)

On the quarter circular barrier:     (9b)

On the vertical barrier:      (9c)

4. Thermophysical properties

The thermophysical properties of NAFs are directly affected by the thermophysical characteristics of both the NAP and the BAFs. Table 1 presents the thermophysical properties.

Table 1. Thermophysical characteristics of BAFs and materials at standard ambient temperature.

Items (bf, p)	Cp (Jkg-1K-1)	ρ (kgm-3)	κ (Wm-1K-1)	μ (kgm-1s-1)	σ (Sm-1)	β (K-1)
ZnO	495.04	5610	29	-	16.9×106	3.02×10-5
Co	420	8900	100	-	16.02×106	1.3×10-5
Fe3O4	670	5180	80.4	-	0.112×106	20.6×10-5
Kerosene	2090	780	0.149	0.00164	6×10-10	99×10-5
Water	4179	997.1	0.613	0.001003	5.5×10-6	21×10-5

5. Computational procedure

We solved the governing dimensionless equations (3)-(7) in conjunction with the BACs (9) using the GEF scheme. Codina [26] and Zienkiewicz et al. [27] have extensively analyzed and explained this numerical method. It utilizes the process of dividing the solution domain into finite element meshes composed of nonuniform triangular elements. In this study, we have used six-node triangular elements, which have also been used in previous works by Rahman et al. [28], and Uddin and Rahman [29]. Each of the six nodes is linked to velocities, temperature, and isoconcentration. However, pressure is exclusively related to corner nodes. As a result, a polynomial of a lower degree is chosen for pressure, which fulfills the continuity equation. When dealing with linear elements, pressure is considered discontinuous between the elements to avoid having the same pressure over the entire domain. Afterward, the nonlinear governing partial differential equations are converted into a set of integral equations using the GFE approach. Gauss's quadrature method is utilized to integrate each term in these equations. The nonlinear algebraic equations that arise are subsequently adjusted to include the BACs. The N-R iteration procedure has been used to solve a global set of nonlinear algebraic equations in matrix form. These equations were solved using an in-house built solver through the MATLAB interface. The convergence criterion for the numerical solutions, , has been defined as a function of the general dependent variable and the number of iterations m.

5.1. Mesh generation

In the finite element method, mesh building involves dividing a given domain into smaller sub-domains called finite elements. The numerical grid establishes the discrete positions, where the variables are calculated. It provides a distinct and precise representation of the geometric region where the problem must be solved. The GFE procedure is a highly effective tool for resolving boundary value problems in engineering applications because it can handle complex geometries. Figure 2 depicts the arrangement of the mesh in the current physical domain, utilizing triangular finite elements.

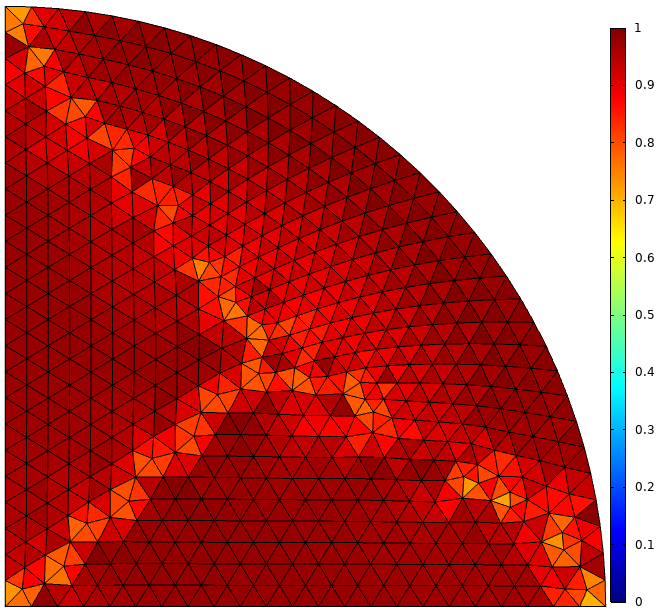
5.2. Grid independency test

Grid refinement research has been conducted for R_a=10⁵, H_a=25 and Pr=6.8377 in a quarter circular. We are now analyzing six non-uniform grid systems, each with a unique number of elements within the resolution field: 300, 494, 1115, 1797, 2788 and 47193. The numerical analysis was conducted to determine the precise key in the average Nu for the aforementioned elements to assess the grid fineness. The consequences are presented in Table 2. For our simulation, we used extra-fine rather than extremely fine grids, as the Nusselt numbers corresponding to these grids differ by less than 1%.

Table 2. Grid sensitivity check at ,,, , for Fe₃O₄-kerosene nanofluid.

Grid	Coarse	Normal	Fine	Finer	Extra fine	Extremely fine
Number of elements	300	494	1115	1797	2788	47193
Nuave	7.9947	8.672	9.8161	10.420	10.969	10.971

5.3. Code validation

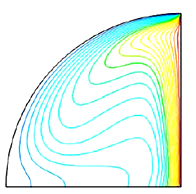
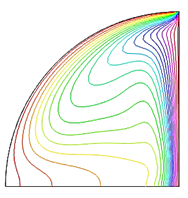
To evaluate the precision of the numerical method employed to solve the specific problem, we compared our simulated results with Kent et al. [30]. Kent et al. [30] examined HTR's uninterrupted and seamless movement through natural convection pathways inside a triangular area with straight boundaries. Figure 3 compares the results obtained using the current numerical code with the outcomes reported by [30] about isotherms at various Rayleigh values. The computed results demonstrate a remarkable level of agreement with the answer reported by Kent et al. [30]. This validation enhances trust in the numerical results obtained from the current study.

Ra Kent et al. [30] isotherms. Present study isotherms.

10³
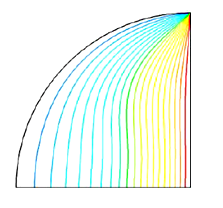
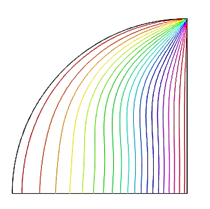
10⁴
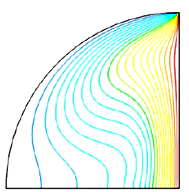
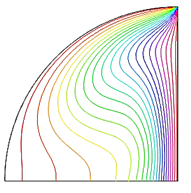
10⁵

6. Results and discussion

We will analyze the numerical consequences of free convective HTR of six different sorts of NAFs in a quarter-circular enclosure, including physical and technical aspects. This exploration involves studying the physical phenomena across a wide range of regulatory parameters. We specifically examine the Fe3O4-kerosene nanofluid during the numerical simulations to analyze the flow and thermal fields. Additionally, we calculate the average Nu by considering several model factors that affect the problem. The consequences are analyzed by varying NAP volume fraction, Hartman number and magnetic field period The inquiry has expanded to scrutinizing the mean Nusselt numbers of six categories of nanofluids at different solid volume fractions, provided in a tabular style. Moreover, a comprehensive study has been carried out to compare the possessions of various factors such as magnetic field period, nanoparticle volume fractions, Hartmann numbers, and nanoparticle diameters. Every outcome is accompanied by a brief yet thorough explanation to help comprehension.

6.1. Average HTR rate for different NAFs

The results obtained thus far pertain to Fe3O4-kerosene nanofluid configuration. To understand how the results vary with dissimilar nanofluids, we explore combinations of numerous BAFs and NAPs. Table 3 presents the average Nu on the bottom heated barrier for two distinct base fluids, namely water (H2O) and kerosene, each paired with three dissimilar types of NAPs: ZnO, Co, and Fe3O4. From the table, it is evident that for all six types of nanofluids, an upsurge in the volume % leads to a corresponding intensification in the average Nu. Notably, the NAF Co-Ke exhibits a higher average Nu compared to the other five types of NAFs. Specifically, the HTR augmentation rates for kerosene-based NAFs, namely Fe3O4, ZnO, and Co are 1278.1%, 1001.8%, and 1258.7%, respectively, when compared to the corresponding base fluids for a nanoparticle volume fraction of 5%. Conversely, the HTR rates are 449.4%, 470.2%, and 492.6% for H2O-based similar nanofluids.

Table 3. Average Nu on the heated barrier for dissimilar NAFs and different  when ,, λ =0.5.

Nanofluids	Φ	Nuave	Increase (%)
Fe3O4-water	0.0 0.01 0.02 0.05	9.8054 11.815 13.673 18.599	- 200.96 185.8 492.6
ZnO-water	0.0 0.01 0.02 0.05	9.8054 11.833 13.659 18.361	- 202.76 182.6 470.2
Co-water	0.0 0.01 0.02 0.05	9.8054 11.771 13.528 18.022	- 196.56 175.7 449.4
Fe3O4-Kerosene	0.0 0.01 0.02 0.05	9.8275 15.4570 20.371 32.958	- 562.45 491.4 1258.7
ZnO-Kerosene	0.0 0.01 0.02 0.05	9.8275 14.340 18.275 28.293	- 451.25 393.5 1001.8
Co-Kerosene	0.0 0.01 0.02 0.05	9.8275 15.738 20.834 33.615	- 591.05 509.6 1278.1

6.2. Impacts of periods of the magnetic field, nanoparticles volume fraction, Hartmann number and particle diameter on HTR

In this section, we examine the HTR rate for various parameters to elucidate the influence of different magnetic field periods. Figure 4 portrays the average Nu on the bottom heated barrier for dissimilar nanoparticle volume fractions under varying magnetic field periods, while keeping other parameters fixed as Ha=50, Ra_T=10⁶ , Ra_c=10⁵, d_p=10nm, n=3, y=15° for Fe₃O₄-kerosene nanofluid. Observations from the figure reveal that with an intensification in both NAP volume fraction and magnetic field period, there is a corresponding rise in the average Nu, indicative of an enhancement in the HTR rate.

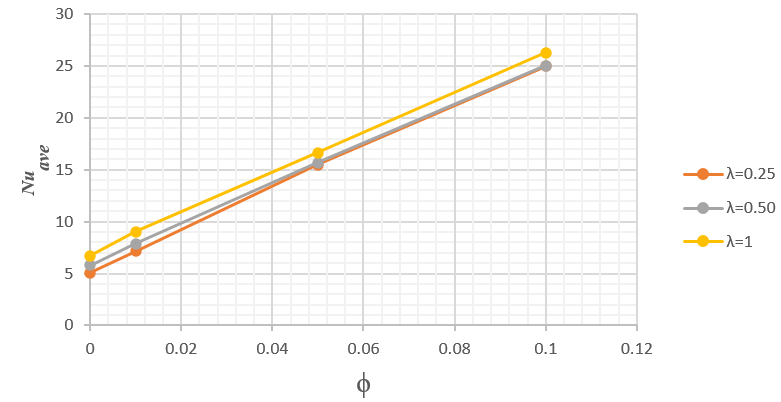
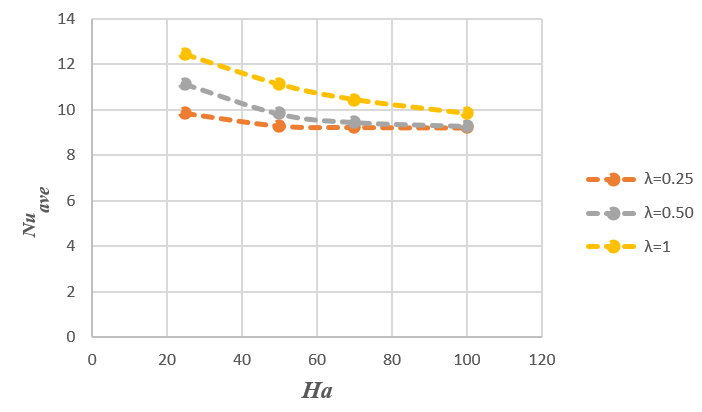
Figure 5 illustrates the average Nu for Fe3O4-Kerosene nanofluids on the bottom heated wall for dissimilar Ha and various magnetic field periods, while other parameters are constant at Ra_T=10⁶, Ra_c=10⁵, Φ=0.02, d_p=10nm, n=3, y=15° and . With the increment of Hartmann number, the average Nu decreases though its intensifications with the increment in magnetic field period.

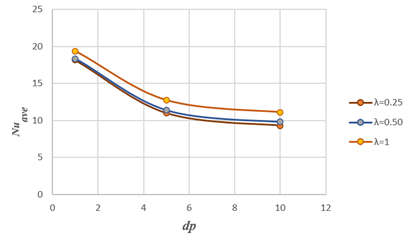
The combined impacts of nanoparticle diameter and the applied magnetic field on the average Nu values are portrayed in Figure 6, for the default parameter values Ra_T=10⁶, Ra_C=10⁵, Ha=50, Φ=0.02, n=3, and y=15°. As the nanoparticle diameter increases, the average Nu decreases despite increasing with the increment in the magnetic field period.

6.3. Effect of shape factor on HTR

The displayed results only examine nanoparticles with a spherical shape. The contemporary work scrutinizes the impact of different NAP shapes on the increase of thermal transmission in nanofluids. Figure 7 demonstrates the average Nu for Fe₃O₄ nanoparticles of dissimilar forms, such as sphere, brick, cylinder, platelet, and blade, as a function of NAP volume fraction. Based on the above figure, it is evident that the average Nu is more significant for the blade-shaped NAPs compared to the spherical ones. It is because the blade-shaped particles have a lower degree of roundness, resulting in a greater overall surface area of the solid-liquid interface compared to the surface area of the liquid interface with spherical-shaped nanoparticles, even when the same volume fraction of nanoparticles is present.

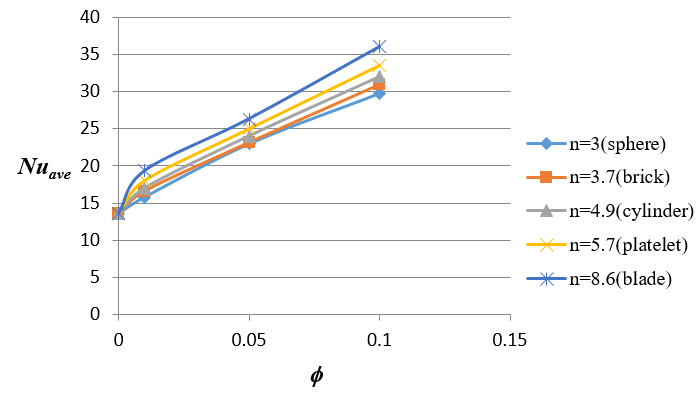
Furthermore, the alteration in the mean Nu becomes increasingly evident as NAPs increase. The image shows a series of heat transfer performances, ranked from highest to lowest, based on the nanoparticles' forms. The order follows blade, platelet, cylinder, brick, and sphere.

6.4. Response surface methodology

Using mathematical and statistical techniques, specifically response surface methodology (RSM), is beneficial for modeling and analyzing issues involving numerous variables affecting interest response. It is extensively employed in several areas, such as engineering and manufacturing, to improve and understand intricate procedures. Researchers can use mathematical models to analyze the interactions between factors and responses to discover the most efficient conditions for maximizing heat flow. RSM is essential in applications like heat exchangers and temperature control systems. The contemporary study demonstrates the encouragement of the independent variables (ϕ, Ha, and λ) on the response (RES) function Nuave while employing the statistical RSM. The quadratic polynomial model's structure is established in the following manner:

(10)

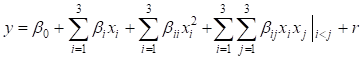
In equation (10), y is the output function, B₀ represents the intercept term, and B_i represents the regression coefficient for the linear term of the factor x_i. The regression coefficient for the quadratic term of the i^th factor is denoted by B_ii, and the quadratic term of the i^th and j^th factors is represented by B_ij. The error value is specified as r. In addition, Nuave is considered to be the responsive faction (y), with the associated input variables being ϕ, Ha, and λ. The statistical model is defined by the number of parameters, their levels, and the particular arrangement of 20 runs. Table 4 provides a clear picture of CCD's hierarchical layers of input variables.

Table 4. Implemented levels and design factors for central composite scheme.

Variables	Levels
	-1(low)	0(medium)	1(high)
ϕ	0	0.02	0.04
Ha	20	60	100
λ	0.25	0.5	0.75

RSM has generated the following general models for assessing the relationship between the RES variable Nuave and the effective input parameters (ϕ, Ha, and λ). The mathematical correlation provided the link between the RES function Nuave and the input variables (φ, Ha, and λ):

Nuave= 16 + 4.95 ϕ - 1.74 Ha + 3.49 λ + 1.18 ϕλ - 1.58 Ha λ

(11)

6.5. Response surface study

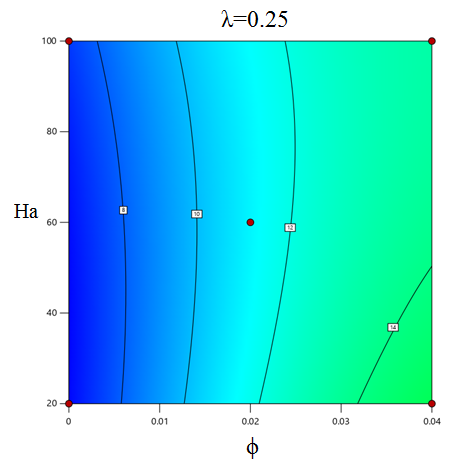
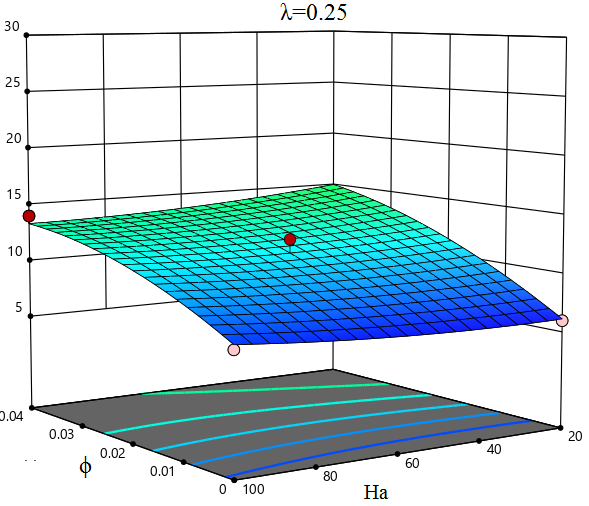
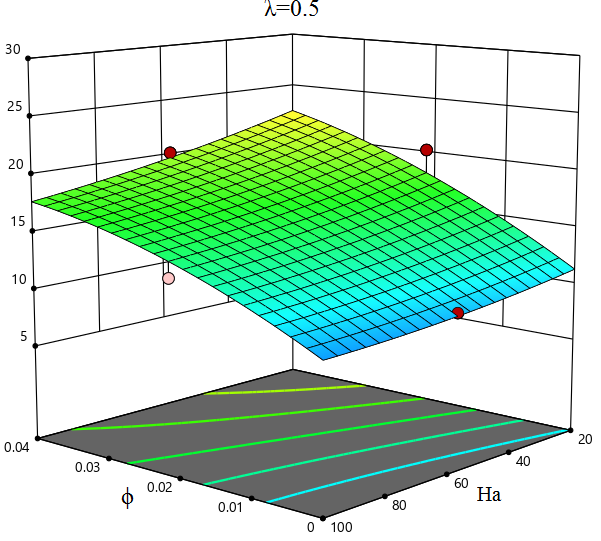
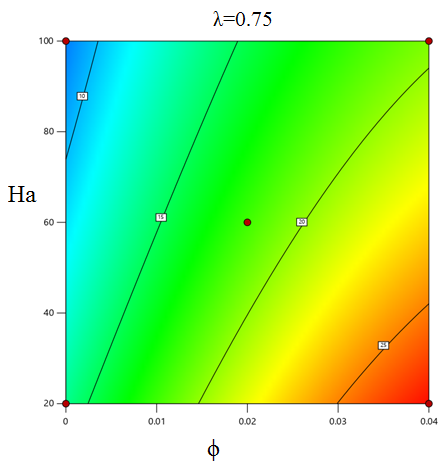
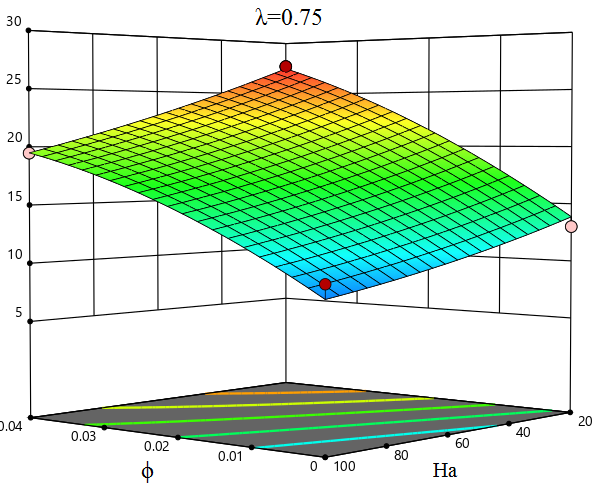
A response surface plot is a graphical representation that illustrates the relationship between several independent parameters (ϕ, Ha, λ) and the response variable Nuave. It is built utilizing computer techniques like response surface analysis. The response surface plots in Figure 8, illustrate the investigation of the possessions of ϕ, Ha, and λ on Nuave using response surface methods. The graphs are displayed in both two-dimensional and three-dimensional formats. Figure 8 demonstrates the interaction between ϕ and Ha, showing that as ϕ increases and Ha decreases, Nuave intensifications while another factor, λ, remains constant. Nuave exhibits its uppermost value with ϕ of 0.04, Ha value of 20, and λ value of 0.75. Conversely, it reaches its lowest value at ϕ of 0, Ha value of 100, and λ value of 0.25.

6.6. Sensitivity Analysis

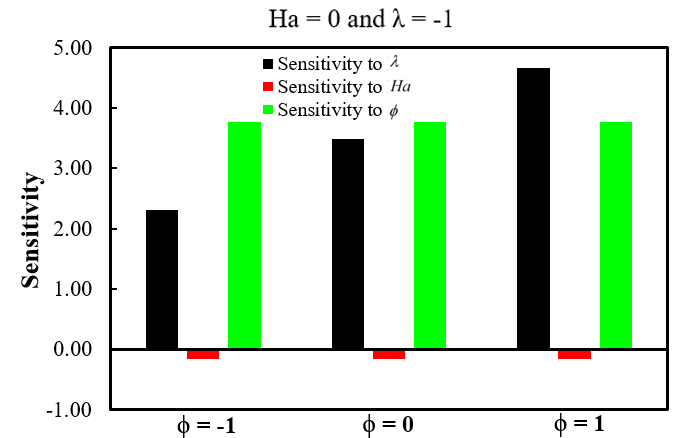
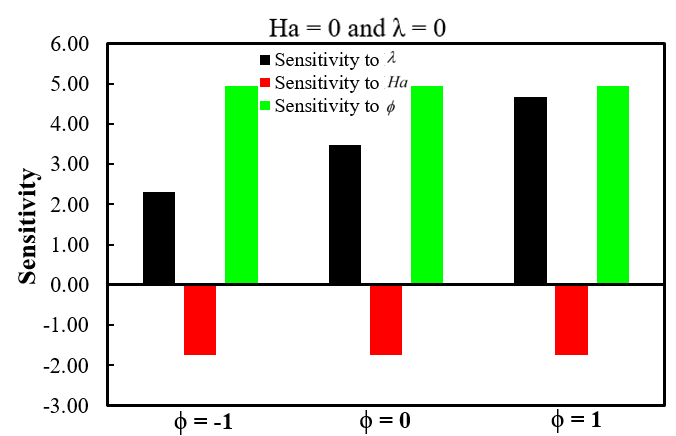
Sensitivity (SNY) scrutiny is a vital technique in studying convection in nanofluids as it elucidates the impact of modifications in different factors on the study's outcome. Various factors can influence the pace at which heat is transferred in NAF's free convective HTR process. Performing a sensitivity analysis allows us to identify the most relevant aspects and comprehend their impact on the rate of HTR. These aids contribute to the optimization of the system's design and the enhancement of its presentation. Moreover, the SNY study can assist in identifying the locations where the HTR rate is most vulnerable to parameter variations. This study entails the computation of the partial derivatives of the dependent variable Nuave with regard to the independent variables ϕ, Ha, and λ. By changing the values of the independent variables at three separate levels (low, medium, and high) represented by the numbers -1, 0, and 1 correspondingly, we effectively obtained the desired outcomes. The regression Equation (11) is utilized to ascertain the SNY. The measurement of SNY involves the calculation of the partial derivative of the output function Nuave about the independent factors [31].

The subsequent sensitivity functions of the response function are as follows:

= 3.49 + 1.18 ϕ - 1.158 Ha                                     (12)

= -1.74 - 1.58 λ                                                          (13)

= 4.95 + 1.18 λ                                                           (14)

A positive SNY output signifies that growth in the input variable value leads to a direct enhancement in the output function value. Moreover, a negative SNY value indicates a reduction in the output function caused by a rise in the input variable [32]. Figure 9 and Table 5 present the sensitivity study of the output response Nu_ave varying ϕ, Ha, and λ values. The data illustrates that the SNY of λ and ϕ are positively correlated, while the SNY of Ha is negatively correlated. Due to its damping effect on flow and HTR, Ha exhibits a negative sensitivity. Increasing Ha enhances the electromagnetic forces, resulting in a diminution in fluid flow and a corresponding reduction in the rate of HTR. Therefore, the relationship between Ha and Nu_ave is inverse, meaning that an upsurge in Ha leads to a diminution in Nu_ave. Conversely, the variables λ and ϕ favorably impact the Nu_ave due to their direct effect on fluidic flow and HTR. Raising these parameters can enhance the HTR rate. Out of these parameters, ϕ has the most SNY on Nu_ave since even a slight adjustment in ϕ (2%, 4%) significantly intensifies the HTR rate compared to λ.

Table 5. Sensitivity study of Nu_ave.

Ha	λ	ϕ
0	-1	-1	-0.16	2.31	3.77
		0	-0.16	3.49	3.77
		1	-0.16	4.67	3.77
	0	-1	-1.74	2.31	4.95
		0	-1.74	3.49	4.95
		1	-1.74	4.67	4.95
	1	-1	-3.32	2.31	6.13
		0	-3.32	3.49	6.13
		1	-3.32	4.67	6.13

(a) (b)
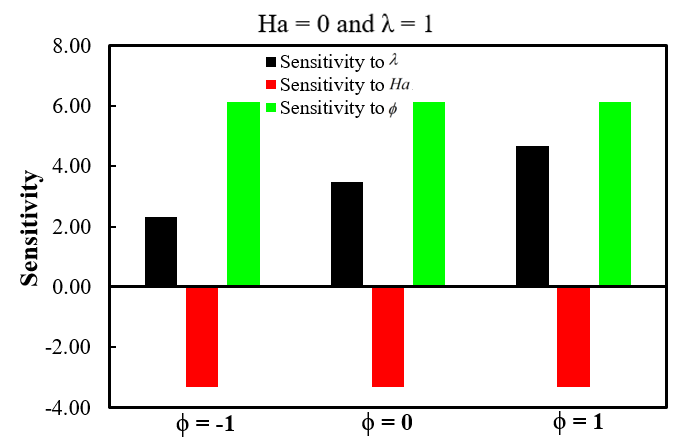(c)

Table 6. Optimum values using RSM.

Parameter	Optimum value
Ha	20
ϕ	0.04
ϕ	0.75
Nuave	27.75

6.7. Optimization investigation

RSM is useful in determining the minimum and maximum values of one or more replies. One can analyze the contour plot of the response surfaces generated by the regression models to identify the optimal circumstances for numerous responses, such as product and growth. This graphical optimization lets us determine the exact region in the parameter space, locating the area that satisfies the optical criteria. The op optimization research of an experimental design is evaluated by three unique methods: numerical analysis, graphical analysis, and point prediction. In the domain of numerical optimization, the selection of responses and factors is contingent upon the particular purpose of the investigation. The responses produced three modes- report, ramps, and bar graph- about the same problem. The optimal values of the parameters being analyzed are presented in Table 6.

7. Conclusions

This study focuses on statistically investigating the convective flow of NAFs in a quarter-circular-shaped region. The goal is to understand the HTR mechanisms and determine the optimum heat enhancement in NAFs compared to BAFs applying RSM. The flow and thermal behaviors are visually shown through graphical displays and response surface plots, showcasing the numerical results. The study primarily focuses on the physical perspective to analyze the numerical implications. The fundamental discoveries of the research can be summarized as follows: An intensification in NAP volume fraction leads to a substantial intensification in the average Nu. A drop in the Ha and nanoparticle diameter leads to an upsurge in the average Nu. The thermal transmission rate is directly proportional to the intensification in the period of the MAF. NAPs with blade-shaped morphology exhibit an enhanced heat transfer rate. Kerosene-based nanofluids demonstrate superior heat transmission capabilities compared to water-based nanofluids. The Co-kerosene NAF has the greatest average Nu of all studied nanofluids. The HTR rate is highly responsive to variations in the Ra and the NAP volume percent parameters. The HTR rate has a lower level of sensitivity to the Ha parameter. The optimum HTR is achieved when Ha = 20, ϕ=0.04, and λ = 0.75 while keeping the other parameters unchanged.

Conflict of Interests

The authors assert that there are no conflicts of interest.

Nomenclature

References