Journal of Fluid Flow, Heat and Mass Transfer (JFFHMT)

ISSN: 2368-6111

The Impact of Collisions on Heat Transfer in a Particle-Laden Shearless Turbulent Flow

Hamid Reza Zandi Pour¹, Michele Iovieno¹

¹Politecnico di Torino, Dipartimento di Ingegneria Meccanica e Aerospaziale
Corso Duca degli Abruzzi 24, 10129 Torino, Italy
hamid.zandipour@polito.it; michele.iovieno@polito.it

Abstract - In this research, we undertake an investigation of a turbulent flow seeded with heavy inertial particles, employing Eulerian-Lagrangian point-particle direct numerical simulations in the two-way coupling regime. The primary objective of our investigation is to assess the influence of inter-particle collisions on heat transfer within the time-evolving thermal mixing layer that develops between two regions with distinct temperatures in a homogeneous and isotropic turbulent flow. Our findings encompass a range of Stokes numbers spanning from 0.2 to 3, while maintaining a thermal Stokes number to Stokes number ratio of 4.43, at a Taylor microscale Reynolds number up to 124. Our results reveal that particle collisions tend to diminish the correlation between particle temperature and velocity, consequently leading to a marginal reduction in the average heat transfer when compared to a collisionless regime at higher Stokes numbers.

Keywords: Heat transfer, Particle-laden flow, Turbulent mixing, Inter-particle collisions.

© Copyright 2023 Authors - This is an Open Access article published under the Creative Commons Attribution License terms Creative Commons Attribution License terms. Unrestricted use, distribution, and reproduction in any medium are permitted, provided the original work is properly cited.

Date Received: 2023-08-20
Date Revised: 2023-10-05
Date Accepted: 2023-10-25
Date Published: 2023-11-07

1. Introduction

Numerous natural and industrial phenomena contain a turbulent flow whose dynamical and thermal evolution is highly coupled with the solid particles that are carried by the flow. Such complex flow regime can be seen in chemical processes, pollutant dispersion in atmosphere, particle transport systems, clouds, plumes, industrial separators, cyclones and sediment transport systems. Therefore, the ubiquity of this peculiar flow has made it an active area of research in many various applications and it has been under numerical and experimental investigation for decades. On the other hand, particle-particle collisions play a significant role in particulate turbulent flows even in relatively diluted suspensions. The effect of collision has been under investigation since the state-of-the-art work of Saffman [1]. For instance, collisions between water droplets in clouds are a necessary condition for precipitation formation from cloud droplets and ice crystals, while, particle-particle collisions have a profound impact on the onset and evolution of sandstorms [2]. In these processes, the background turbulence of the carrier flow favors inter-particle collisions. The mechanisms of the collision rate enhancement by background turbulence have only become clear in the past few years, and the underlying physics is currently qualitatively well understood, although quantifying the rate of small particles collisions suspended in a turbulent flow may require more advancement. As a pioneering work on the collision effect in particle-laden turbulent flows, Saffman et al., developed the theory of collision of water droplet in cloud physics and they could formulate the droplet collision rates for identical small low-inertial droplets in terms of droplet dimension and turbulence characteristics (the rate of turbulent kinetic energy dissipation and the kinematic viscosity of fluid ). Their findings suggested that the collision frequency of the small droplet suspended in clouds is independent of droplet properties [1]. However, in the subsequent works like the work of Sundaram et al., it was found that droplet properties also influence the collision rate. The results of Sundaram et al., showed that particle parameters such as particle response time, number density and size can impact collision frequency as well as background turbulence. They showed the significant dependency of the collision rate on the droplet Stokes number [3]. There have also been detailed theoretical investigations of the collision rate, a particularly effective description of the collision-rate enhancement in terms of a stochastic model for the probability distribution function (pdf) of pairs of particles has been proposed by Zaichik et al. [7]. They have studied collision rate enhancement resulting from two different mechanisms for high and low inertial particles. Recently, the effect of par- ticle high inertia on collision rate which is understood as sling effect has been studied by [8, 9, 10]. This effect at high particle inertia can cause finite time singularities in particle velocity tensor leading to a multi-valued particle velocity. As a results of this effect, collision rate can be increased due to the particle trajectories crossing at high Stokes number. Despite the numerous experimental works which have been done on single-phase turbulent flows, very little experimental investigations exist concerning particle-laden flow and collisions of suspended particles, primarily due to the difficulties in Lagrangian measurements. The problem is even worse when other phenomena, like fluid-particle heat transfer or particle collisions, are studied [2]. In fact, the long-standing experimental tools for investigating turbulent flows, such as hot-wire anemometry, at best only provide data on the velocity field and its spatial correlation function. Over the past few decades, new techniques have been developed, employing on fast-imaging to follow particles in turbulent flows. Such developments in experimental tools and methods have led to collecting a very new information about the motion of particles in turbulent flows, yet detecting collisions between a large number of tiny particles in a well-controlled laboratory experiment is not possible [4]. FFor instance, near-wall interaction of particles in wall-bounded flows has been investigated recently by [5, 6] to study of particle-wall interaction in configuration which a solid wall is present. Therefore, direct numerical simulations (DNSs) have been always an important tool to obtain detailed results on features which cannot be directly measured. In fact, DNS provides a powerful tool to extend the existing insights into complex flow regimes like particle-laden turbulent flows, even if it is still limited to relatively low to medium Reynolds numbers due to the need for huge computational resources. n non-isothermal turbulent flows, the interaction between fluid and particles in terms of thermal properties has been explored in several works, mainly using the point-particle approach that applies to small sub-Kolmogorov particles. Most of the research has focused on channel flows [11, 12, 13, 14, 15] and homogeneous turbulence [16, 17, 18, 19]. However, recently, a few studies have examined the fluid-particle thermal interaction in the time-evolving shearless thermal mixing layer generated at the interface between two fluid regions with different temperatures. This configuration can serve also as a benchmark for turbulence models. The studies investigated both one-way and two-way coupling regimes [20, 21], with a focus on collisionless suspensions and the impact of particle inertia and Reynolds number.

Furthermore, collisions between particles play a crucial role in heat transfer in fluidized beds because heavy particles are able to cross the wall thermal layer, thus transferring heat between the wall and the core region of the pipe. However, in such applications, volume fractions are high, usually on the order of 10⁻² [22], well above the limit of two way coupling between point particles. Only a few theoretical works have considered the effect of collisions on heat transfer, such as [23], who studied the heat transferred between elastically colliding spherical particles. Collisions are usually not taken into account when analyzing heat transfer by particles in a turbulent flow, despite their increased frequency with higher volume fractions. Carbone et al. [17] studied the effect of particle-particle collisions on temperature statistics in homogeneous and isotropic turbulence in the one-way cou- pling regime at low Reynolds numbers, finding a minor effect on small scale temperature statistics. However, collisions can decelerate small particles while accelerating large ones, result- ing in an enhanced velocity scattering that can affect particles’ ability to carry enthalpy over long distances in the presence of a strong temperature gradient. This scattering impacts how the presence of particle particles can enhance heat transfer compared to an unseeded flow [20, 21].

To investigate how inter-particle collisions impact heat transfer and fluid-particle correlations, we expanded on our previous research by examining the effect of elastic collisions in the simplest inhomogeneous flow configuration already considered in [20, 21]. In this configuration, heat is transferred between two regions at different temperatures through a statistically steady homogeneous and isotropic velocity field, creating a mixing layer at the boundary between the two regions where fluctuations of temperature and velocities correlate. We compare single-point statistics with the collisionless regime in the same overall flow configuration [20, 21]. In section 2, we provide a detailed description of the physical model and numerical methods used to simulate the collisional turbulent gas-particle flow. In section 3, we discuss the results from our simulations. A comparison between the relative particle-to-fluid velocity-temperature correlation variation in terms of Stokes number and Taylor micro-scale Reynolds number for collisional and collisionless flow regimes, as well as an analysis of the temperature of colliding particles is included. Finally, in section 4, we provide a brief summary of the main conclusions.

2. Physical model

2.1 Governing equations

In this study, we use an Eulerian-Lagrangian approach to model the dynamics of a non-homothermal incompressible flow seeded with particles. We distinguish between the continuous fluid phase and the discrete particle phase, with temperature variations assumed to be small enough to not significantly change fluid density. Therefore, within these hypotheses, the fluid phase is represented by the following system of equations:

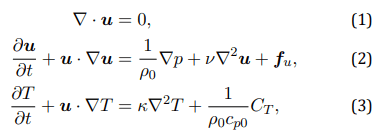
where u(t, x), T (t, x), and p(t, x) are the fluid velocity, temperature, and pressure fields, respectively. The constants ρ₀, c_p0, ν, and κ represent the fluid density, isobaric specific heat capacity, kinematic viscosity, and thermal diffusivity, respectively. The body force f_u is introduced to maintain turbulent fluctuations in a statistically steady state, and C_T is the heat exchanged per unit time and unit mass with particles, representing the particle thermal back reaction on the flow. Similarly to previous works (e.g. [17, 18, 20, 21]), we assume a oneway coupling regime for momentum exchange, so that no force is exerted by particles on the fluid. This assumption holds true in dilute regimes, as previous works have found that momentum feedback has a minor thermal effect on fluid temperature statistics [17]

We consider the motion of a set of identical small, rigid spherical particles. The particles are assumed to have a radius R much smaller than the Kolmogorov length-scale η so that they are considered material points. They have a mass density much greater than the fluid density, making the Stokes drag force the dominant term in the Maxey-Riley equation [24]. An equation for the particle temperature can be derived under the same assumptions. Thus, the dynamics of each particle can be described by the following equations:

where x_p(t), v_p(t), and ϑ_p(t) are the position, velocity, and temperature of the p-th particle, respectively. The momentum and thermal relaxation times τ_v and τ_ϑ are given by

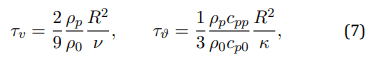
where ρ_p and c_pp denote the particle density and specific heat at constant pressure. Particle-particle interactions, other than collisions, are not considered. The particle thermal feedback per unit time and unit volume in equation (2) is given by

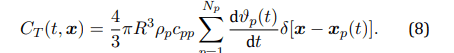
where δ(·) is the Dirac delta function.

2.2 Flow setup and numerical method

We investigate the heat transfer between two homogeneous regions with different temperatures, T₁ and T₂ < T₁, in a homogeneous and isotropic velocity field. To simulate this phenomenon, we solve the governing equations described in Section 2.1 in a parallelepiped domain with dimensions L₁ = L₂ and L₃ = 2L₁ along the x₁, x₂, and x₃ directions. The initial temperature distribution is set to T₁ in the half- domain where x₃ < L₃/2 and T₂ in the half-domain where x₃ > L₃/2.

We apply periodic boundary conditions to the velocity field on all faces of the domain, while for temperature, we de- compose it into a mean linear field and a fluctuating part, as described in [20, 21]. This allows us to apply periodic bound ary conditions to the fluctuating part of the temperature field. Any particles that exit the domain are reintroduced on the opposite side.

The governing equations (1-8) are made dimensionless by using L₁/2π as length scale, a velocity scale deduced from the imposed kinetic energy dissipation rate ε, and the temperature difference T₁  T₂ as temperature scale [20, 21]. To make the results more physically significant, the Taylor-microscale is used as the reference length in the definition of the Reynolds number. In the dimensionless form, the flow is governed by the Reynolds number Re = uⁱλ/ν, the Prandtl number Pr = ν/κ, and the particle-to-fluid heat capacity ratio ϕ_ϑ = ϕ(ρ_pc_pp)/(ρ₀c_p0), where ϕ is the particle volume fraction. The particle dynamics are described by the Stokes numbers, which represent the ratio between their relaxation times used in the adimensionalization. Thus, the Stokes num- ber St = τ_v/τ_η and the thermal Stokes number Stϑ = τ_ϑ/τ_η are used to describe the particle dynamics. All relevant flow parameters are listed in table 1.

A fully dealiased pseudospectral method, using the 3/2- rule, was employed to discretize the spatial domain of the fluid phase equations (1–3). The forcing function f_u was defined in Fourier space as where ε denotes the energy injection rate, equal to the kinetic energy dissipation in statistically steady conditions, and κ_f is the forced wavenumber. Interpolation of fluid velocity and temperature at particle positions, and computation of the particle thermal feedback (8), were carried out using a recent nu- merical method [25, 26] based on inverse and forward non-uniform fast Fourier transforms with a fourth-order B-spline basis. Integration in time was performed for both the carrier flow equations (1–3) and the particle equations (5)–(6) using a second order exponential integrator.

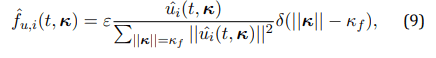
2.3 Inter-particle collision model

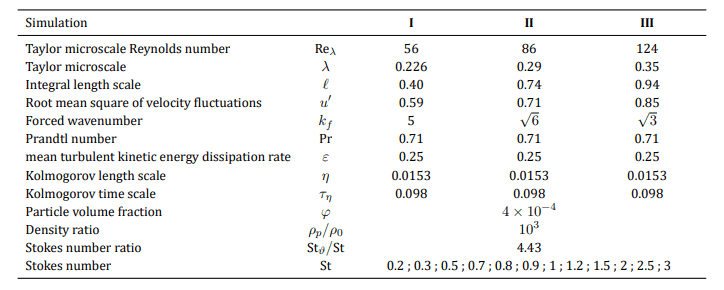
In this study, we focus on elastic binary collisions that occur when the distance between the centres of two particles is equal to their diameter. To introduce these collisions into the numerical simulation, a first-order particle trajectory reconstruction is performed after each time step. Therefore, a collision between the p-th and q-th particles in a time step t ∈ [t_n, t_n+1) occurs when the following equation,

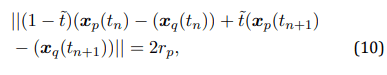
where t˜= (t-t_n)/∆t has a real solution of (10) for t˜∈ [0, 1). In such a case, the positions and velocities of the colliding particles at the end of the time step are obtained from momentum and energy conservation, i.e. they move with the velocity achieved after the collision for the remaining part of the time step. It is assumed that no heat transfer occurs between colliding particles at the impact event and that no direct hydrodynamic interaction, except inter-particle collisions, is taken into account [27]. However, direct collision detection is computationally expensive and not feasible for a large number of particles N_p because it requires 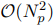numerical operations. To address this issue, the particles are grouped within small boxes, and particle collisions are only detected between particles within the same box. This approach is more practical and computationally efficient. The effect of the box boundaries can be eliminated by shifting the boxes and repeating the algorithm [27].

3. Results

We present a comparison between the heat transfer in the collisional and collisionless regimes in the two-way thermally coupled regimes by carrying out in both regimes simulations according to the parameters in table 1. We used a constant thermal Stokes number to Stokes number ratio, which we have set equal to 4.43, a value representative of water droplets in air. We focus on single-point statistics of fluid and particle temperature and velocity. Since the velocity field is statistically homogeneous and the temperature field is homogeneous in directions x₁ and x₂, all the statistics here presented have been obtained by averaging over planes normal to the inhomogeneous direction x₃, i.e. on (x₁, x₂) planes, so that all statistics are functions of (t, x₃). Due to the finite size of the domain and this plane averaging method, all statistics are affected by some level of noise which produces an uncertainty over the results. The level of uncertainty can be estimated from the fluctuations in the statistics of the fluid and particle velocity fields in the one-way coupling regime, since homogeneity and implies uniform moments. From that we can estimate a relative error of less than 1% in the mean temperature and around 6% in fluid second order moments, while it increases to about 8% in particle second order moments by considering a single simulation. Conditional averages have a larger error, up to 8-10% in the mean temperature difference at collisions, due to the more limited sample size. This error is reduced when also averages on more realizations are considered.

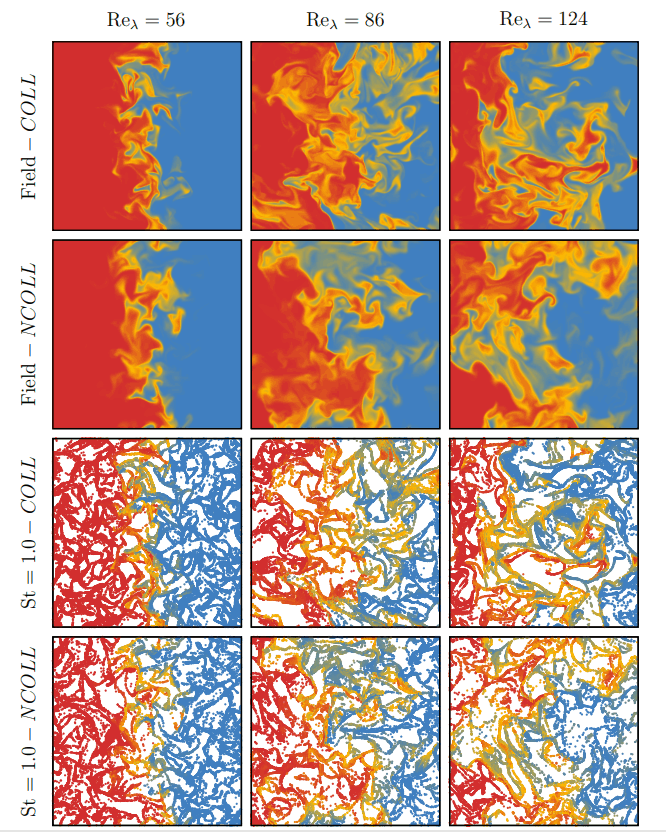
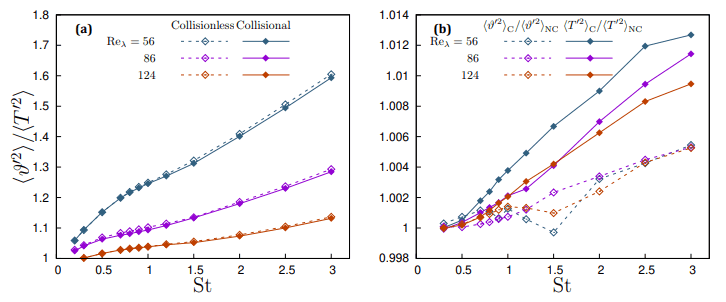
A visualization of the instantaneous temperature of the carrier flow and particles in presented in Figure 1 in a plane parallel to the mean temperature gradient after three eddy turnover times. It shows the mixing of warmer and colder fluid by turbulent eddies as well as particles as they move across the plane initially separating the two regions at different temperatures, being heated or cooled by the fluid in the process. After a transient of a few eddy turnover times, this flow configuration quickly leads to a self-similar stage of evolution where all flow and particle statistics collapse when rescaled with the mixing layer thickness δ. The mixing layer thickness can be defined as (T₁ − T₂)/max{|∂T/∂x3|} [20, 21, 28, 29] and exhibits an almost diffusive time growth. This stage is reached after a few eddy turnover times τ = l/uⁱ, during which a hightemperature variance region develops in the thermally inhomogeneous region

During this self-similar stage of evolution, the particleto-fluid temperature variance ratio remains constant. It can be observed from Figure 2(a) that collisions tend to slightly reduce the variance of particle temperature compared to the fluid temperature, especially at larger Stokes numbers. Due to the particle thermal feedback, the fluid temperature variance increases more than the particle variance, particularly at large Stokes numbers, over the collisionless regime (see Figure 2(b)). However, this difference is small and could only become significant at higher volume fractions.

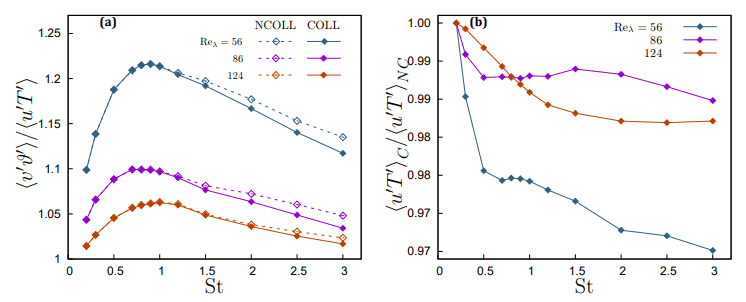
Figure 3 (a) shows the most it important result, the corelation between velocity and temperature fluctuations, which is proportional to the mean heat transfer across the layer separating the two homothermal regions. Indeed, the mean heat transfer in the inhomogeneous direction x₃ is given by

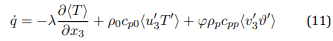
where the first term is the diffusive heat transfer, the second one is the carrier flow convection, and the last one is the particle contribution. Accordingly, to better understand the particle contribution in the mixing layer, turbulent heat flux in inhomogeneous direction x₃ can be normalized by the heat transfer in a static, non-moving system by using the definition of mixing layer thickness δ which is the only relevant length-scale in this flow, i.e. by the heat transfer in a purely diffusive system.

The ratio 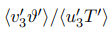is the parameter which gives a measure of the contribution of particles to the heat transfer through the non homothermal layer with respect to the convective heat flux due to fluid turbulent motions. Figure 3(a) shows this ratio for three different Reynolds numbers as a function of the Stokes number. All quantities are computed in the centre of the domain, where correlations have their maxima. During the self-similar stage of the mixing layer the ratio 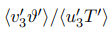does not vary on time, because all fluxes are proportional since they scale with the same δ(t). The ratio has a maximum when the Stokes number is of order one, that is, in correspondence of the highest particle clustering. In the vanishing inertia limit, i.e. when the Stokes number tends toward zero, particles move like passive tracers. However, since in our configuration also the thermal inertia tends to vanish in this limit, because Stϑ/St has been kept constant, thus we have 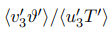→ 1 when St → 0 ⁺. On the opposite limit of very large inertia, when St → ∞, particles velocity and temperature tend to decorrelate from the fluid velocity and temperature, leading to a gradual reduction of 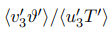. The same trend can be observed at all the simulated Reynolds numbers. Particle inertia gradually modulates the ratio 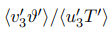, which increases with the Stokes number. Since collisions produce a scattering of the particles, in the two-way coupling regime this results in a different modulation of fluid temperature fluctuations by particle feedback, because collisions reduce the tendency of particles to concentrate in correspondence of large gradients of the advected scalars [17]. However, as figure 4(b) shows, this effect is of minor importance and, at the volume fractions here considered, negligible. 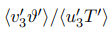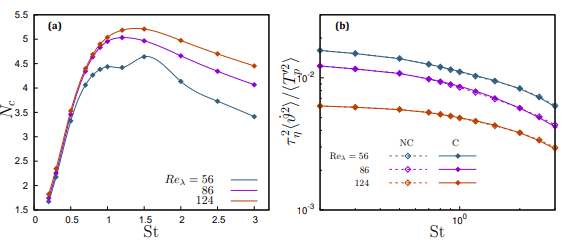Therefore, the variation of can be almost entirely be attributed to the attenuation of the particle temperature-velocity correlation. Indeed, the modification of particle trajectories produces a scattering which decorrelates their velocity from their temperature and, as such, reduces their ability to transport heat over long distances. The collision rate in a turbulent flow tends to be higher for larger particles, because their inertia decorrelate their velocity from the fluid velocity, thus allowing for large relative velocities between particles even at small separations. Coupled with the particle clustering and preferential concentration, which increase local particle densities in low strain regions, the collision rate has a maximum when the Stokes number is of order one, as figure 4(a) shows. As St becomes larger the collision rate slowly reduces and, in the limit St → ∞, would approach the ballistic limit. Anyway, only at large Stokes number, St ≥ 1.5, a significant attenuation can be observed, due to the fact that, notwithstanding the collision rate reduces, the variance of the fluid-particle temperature difference grows much faster with St. According to figure 4(b), 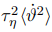becomes constant at low St and scales as St^α, with 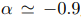at high St, so that 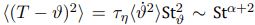. 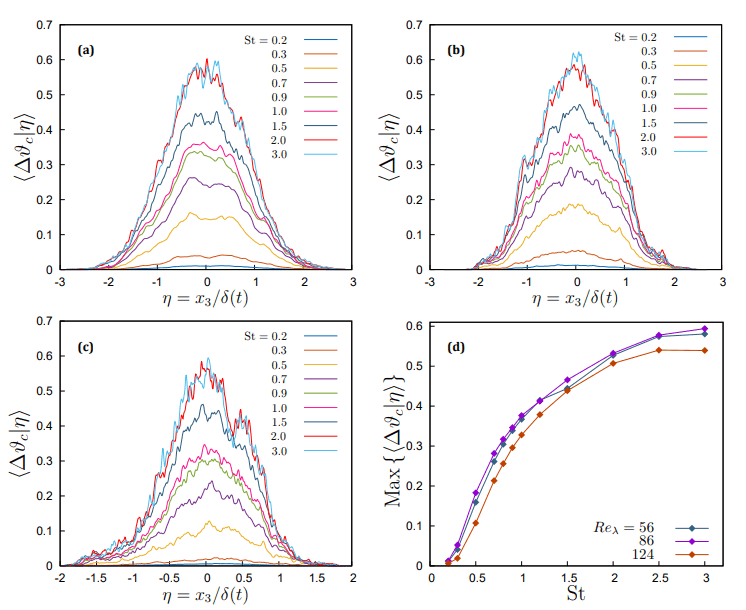The behaviour of particle temperature derivative in this inhomogeneous flow is different from what has been observed in homogeneous turbulence [16], due to the existence of a strong temperature gradient which dominate temperature variations over large scales. This make large particles be able to travel further in the x₃ direction, thus easily enter regions with much different temperatures, so that this leads to the counter intuitive feature that larger particles with a higher thermal capacity experience, in the mean, larger temperature derivatives. While this allows for an increase in the heat transfer, it is also responsible of the more intense reduction of the temperaturevelocity correlation when collisions are taken into account. In fact, collisions between particles with very different temperatures occur between particles coming from distant zones in the inhomogeneous direction, which is possible only for large inertia and thermal inertia, but collisions generates a scatter that modifies their velocity in the x₃ ddirection, not their temperature, thus reducing the 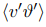correlation. This is clearly visible in figure 5(a,b,c), which shows the mean temperature difference between colliding particles as a function of the normalized position across the thermal mixing layer for different inertia. Larger particles are more able to cross temperature fronts [17], while their larger heat capacity allows them to retain their own temperature, so that they can have very different temperatures when they collide.

4. Conclusion

In this study, we investigated the impact of particle collisions on heat transfer in a dilute particle-laden turbulent flow, with a particle volume fraction kept constant at ϕ = 4 × 10⁻⁴ so that the point-particle approach can be used. We have shown that particle collisions have a minimal effect on the heat transfer when the Stokes number is less than 1, but, when the Stokes number is larger than 1, there is a slight reduction, of about 10%, in the particle-velocity-temperature correlation in the inhomogeneous region where heat transfer occurs. Nevertheless, we can conclude that collisions do not significantly affect the ability of particles to modulate large-scale fluid temperature fluctuations. Based on these results, we infer that incorporating collisions into bulk models of heat transfer in dilute particle-laden flows is unnecessary.

Acknowledgements

The authors acknowledge the CINECA award IsB26_DroMiLa, HP10BU46TS, under the ISCRA initiative, for the availability of high performance computing resources and support. Additional computational resources provided by hpc@polito (http://www.hpc.polito.it) are also gratefully ac- knowledged.

References