Volume 9 - Year 2022 - Pages 177-183
DOI: 10.11159/jffhmt.2022.021
Numerical Investigation of Convective Heat Transfer during Orthogonal Cutting Processes
Thorsten Helmig1, Tim Göttlich2, Hui Liu2, Thomas Bergs2 and Reinhold Kneer1
1RWTH Aachen University, Institute of Heat and Mass Transfer
Augustinerbach 6, Aachen, Germany
helmig@wsa.rwth-aachen.de
2RWTH Aachen University, Laboratory of Machine Tools and Production Engineering
Campus-Boulevard 30, Aachen, Germany
h.liu@wzl.rwth-aachen.de
Abstract - The thermal modeling of machine processes is a key tool to enhance product quality and surface integrity for high precision components. In this context, the cutting zone is of particular interest as significant stresses, temperature gradients and heat sources occur. To accurately model these processes, an FEM-CFD coupling has been developed. In the first step, a FEM chip formation simulation is performed which uses cutting parameters, material models, and mechanical properties. The FEM simulation is performed for an Inconel 718 workpiece. Afterwards, the generated chip geometry, temperature field, and heat source are transferred into a CFD model which quantifies the conjugate heat transfer and corresponding convective heat transfer coefficients at the fluid-solid interface. As recently published work focuses on the development and validation of the interface itself, the work at hand studies the impact of evolving chip geometry on convective heat transfer. Therefore, the continuously evolving chip is approximated by discretizing the geometry development into constant states. Moreover, the investigations are performed in context of a quasi-stationary problem meaning that the tool has performed several cuts and already reached a steady-state temperature field. The analysis shows that the chip has a significant impact on local heat transfer revealing further the heat transfer can be subdivided into two regions: First, a near cutting edge region where chip geometry and fluid temperature impact the heat transfer and second a tool downstream region, where the fluid temperature is the dominating parameter. In total, these results can be used as a basis for future cooling optimization studies.
Keywords: Computational Fluid Dynamics, Conjugate Heat Transfer, Machining Processes, Orthogonal Cutting, Evolving Chip Geometry
© Copyright 2022 Authors - This is an Open Access article published under the Creative Commons Attribution License terms Creative Commons Attribution License terms. Unrestricted use, distribution, and reproduction in any medium are permitted, provided the original work is properly cited.
Date Received: 2022-09-30
Date Accepted: 2022-10-12
Date Published: 2022-11-07
1. Introduction
The recent development of micro- or even submicron technical components places high demands on manufacturing processes and requires detailed knowledge of the occurring thermal phenomena and tool wear [1,2]. Hereby, numerical and experimental research offers the basis for a comprehensive understanding, but is challenging as mechanical, thermal, and even chemical processes occur simultaneously. In particular, the heat source during machining is a key parameter, as the majority of the cutting force dissipates and causes high temperatures in the actual cutting zone [3]. A common approach in this context is the application of cutting fluid to reduce heat sources, improve chip removal and increase lubrication in the cutting zone. To model this process, mechanical and thermal phenomena, as well as their interaction needs to be considered. Regarding the mechanical part and the evolving chip geometry, several experimental and numerical studies have been performed. For example, Chagas et al. [4] presented an FEM to predict the chip geometry and temperature distribution for dry cutting conditions. Regarding experimental investigations, Çolak et al. [5] and Courbon et al. [6] investigated the impact of pressure supply on chip formation as well as removal and highlighted early chip breakage and an extended tool lifetime. However, besides the mechanical phenomena, the impact of fluid dynamics is investigated by means of CFD simulations for various cutting contexts. For example, the group of Eberhard et al. [7] and Oezkaya et al. [8,9] performed intense research on flow modelling in context of drilling tools and tool lifetime.
However, the focus of the outlined work is the mechanical fluid-structure interaction (FSI) without considering detailed conjugate heat transfer between cooling lubricant, fluid, tool, and workpiece. An approach to account for thermal as well as mechanical aspects is presented by Helmig et al. [10] and Liu et al. [11]. Here, the authors use a precalculated FEM-simulation to obtain the chip geometry as well as heat sources. These are following used as input parameters for mesh generation and case setup for a CFD simulation. While the work by Helmig et al. [10] focuses on the experimental evaluation, the work by Liu et al. [11] provides spatially resolved heat transfer coefficients along the tool rake face. However, as the impact of evolving chip geometry on the fluid flow and resulting heat transfer has not been studied yet, this work aims for an improved understanding of local as well as global convective cooling.
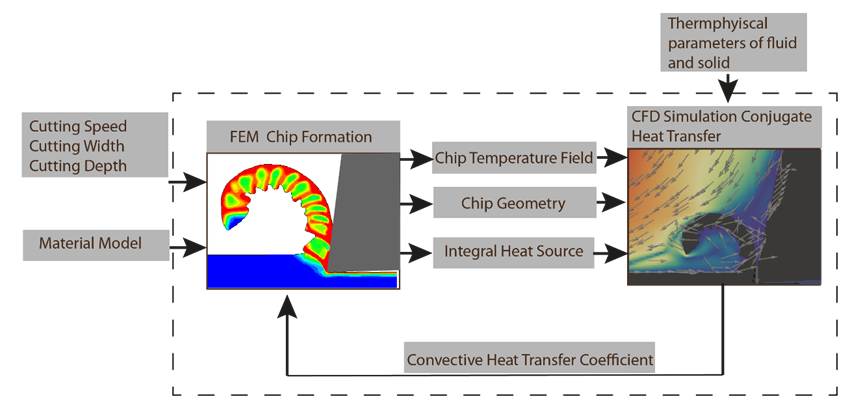
2. Data Exchange Interface and Applied CFD / FEM Methods
To resolve the occurring mechanical as well as thermal phenomena a coupling interface is developed which aims for a reciprocal exchange of results between the two simulations. For development purposes, an orthogonal cutting process is used as a framework as it provides a well-defined and easy to validate environment for experiments. An overview of the interface is given in Figure 1, showing the cutting parameters and material model used as input for the FEM chip formation simulation. In return, the FEM provides the chip geometry and integral heat source used as input for the CFD model. The particular advantage of the flow simulation is the high resolution of the thermal boundary layer to quantify the convective heat transfer coefficients, which are finally returned to the FEM simulation. However, a continuous exchange of geometry and heat transfer coefficients is the long-term goal and not implemented in the current development status. The current interface is capable to hand over discrete states of the chip to the CFD keeping it constant until the next geometry is provided. The feedback of convective cooling on the chip formation is not implemented yet. However, the use of discrete chip geometry is easy to integrate into the existing pre-processing workflow of the CFD setup. For the current dstate, the integration of a continuously moving mesh solver is complex and critical as the trajectory of the moving and evolving chip needs to be defined a-priory to the CFD calculations.
2. 1. FEM Setup
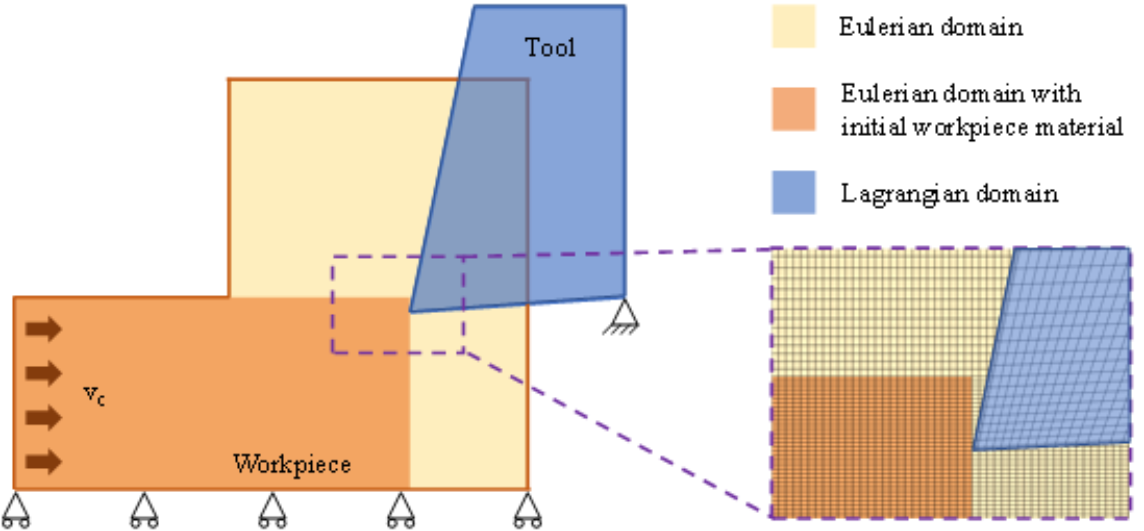
The chip formation process of the orthogonal cutting process is simulated with the Coupled Eulerian-Lagrangian (CEL) method. This CEL method is a feature of the commercial software ABAQUS (version 6.14) and consists of both Lagrangian and Eulerian meshes, as shown in Figure 2. The cutting tool is modeled as a rigid body with the Lagrangian mesh and the workpiece is defined in the Eulerian domain. During the process, the initial workpiece moves at a constant speed vc against the tool through the space- fixed Euler mesh and thus forms an orthogonal cutting. This approach was originally established by Ducobu et al. [12] and Puls et al. [13] and is widely applied. The advantages of the CEL based cutting process simulation is that the Eulerian formulation of the workpiece avoids the mesh distortion, so leading to an increased stability of the simulation.
To model the plasticity of the workpiece, the Johnson-Cook (JC) material model is used. Besides distinct model parameters, the JC model consists of three main factors describing the influence of strain ε , strain rate ![]() and temperature T:
and temperature T:
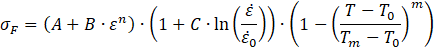
Another essential model for the simulation of cutting processes is the friction model, as it plays a pivotal role in the process forces and heat generation at the tool surface. The simulation in this paper uses a temperature-dependent friction model developed by Puls et al. [14]. The friction coefficient is defined as:
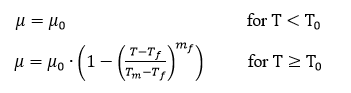
Here, the coefficient of friction between Inconel and cemented carbide has been determined experimentally in [15]. Table 1 summarizes the model parameters for the chip formation simulation of Inconel 718.
Table 1. Model parameters of the Johnson Cook material model for Inconel 718
|
Johnson Cook material constitutive model of Inconel 718 [3] |
||||||||||||||
|
A |
B |
C |
m |
n |
Tm |
T0 |
||||||||
|
[MPa] |
[MPa] |
- |
- |
- |
[°C] |
[°C] |
s-1 |
|||||||
|
1200 |
1284 |
0.006 |
1.2 |
0.54 |
1800 |
25 |
10-3 |
|||||||
|
Johnson Cook damage model of Inconel 718 [3] |
Friction model of Inconel 718 [5] |
|||||||||||||
|
D1 |
D2 |
D3 |
D4 |
D5 |
μ0 |
mf |
Tf |
|||||||
|
- |
- |
- |
- |
- |
- |
- |
[°C] |
|||||||
|
0.04 |
1.2 |
-1.45 |
0.04 |
0.89 |
0.46 |
2.4 |
200 |
|||||||
2.2. CFD Setup
As a framework for the CFD setup, the OpenFOAM open access simulation tool-box is utilized using a solver which considers the transport of mass, momentum and enthalphy for fluid and solid discretized on a two-dimensional cartesian grid. The following properties are considered: time t, spatial coordinate xj, fluid density ρ, velocity component ui, pressure p, enthalpy h, thermal diffusivity a, fluid viscosity μfl and heat source term ![]() :
:
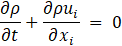
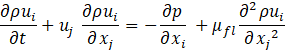
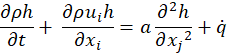
For the fluid inlet a parabolic inlet profile is chosen with values according to the investigated fluid volume flow of about (1.6 l/min). Due to the relatively low Reynolds numbers (Re = 500) a laminar flow is expected and does not require further turbulence modeling. In experimental investigations most of the investigated volume is flooded by the cooling lubricant, therefore flow interaction with surrounding air is expected to have a minor impact in the flow characteristics, in particular near the cutting zone. Hence, a single-phase fluid flow without gas phase is considered. Further, the thermophysical properties of both solid and fluid phase are assumed to be constant. Figure 3 provides an overview of the boundary conditions applied and gives a qualitative impression of the simulation domain also highlighting the thermal coupling of the fluid-solid interface.
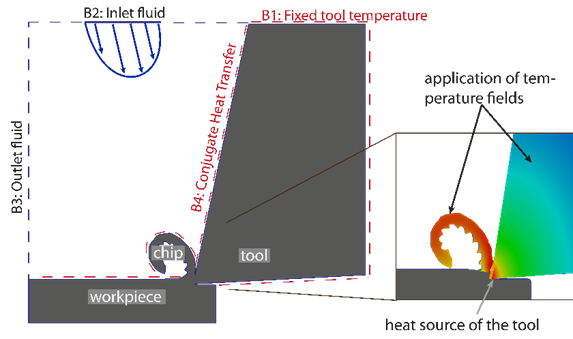
Table 2 Applied Boundaries for Field Values
|
Field |
B1 |
B2 |
B3 |
||
|
Velocity |
- |
Inlet |
Outlet |
No slip |
|
|
Temperature |
Fixed Value |
Fixed Value |
ZeroGradient |
coupled |
|
|
Pressure |
- |
Ambient pressure |
ZeroGradient |
ZeroGradient |
|
2.3. Application of tool and chip temperature field and heat source terms
The integral heat source at the tool tip and the temperature field of the evolving chip is provided by the FEM simulation (subimage in Figure 3 right). While the source term is homogeneously distributed along the tool-chip interface, no particular source term is added at the chip surface, rather the generated process heat is considered by updating the chip geometry and temperature field every 0.2 ms according to the FEM output data. As no additional heat source is applied at the chip, the lubricant flow causes a convective cooling of the chip surface and a minor temperature drop. This effect is expected to be neglectable due to the comparable short simulation time until the next geometry and temperature field are applied. On the long term, the calculated convective cooling for the current geometry will be transferred back to the FEM.
The tool temperature is initialized with a precalculated temperature field used to model a quasi-stationary setting after several performed cuts. The stationary temperature field is obtained by running a simulation with constant chip geometry until no change in tool temperature is observed which typically occurs for physical times of about one second. Regarding further boundary conditions of the tool, a fixed temperature is used. Development and measurement of further boundary conditions (for example a time dependent heat flux into the machine tool) will be part of future research.
3. Results
To get an overview of the flow geometry, the left image in Figure 4 highlights the entire investigated fluid domain, including streamlines to highlight the direction of flow. The flow enters from the top left and is split by the chip and tool into two branches. The first part exits the domain via the left outlet, while the second part moves along the tool surface. As the heat transfer, near the cutting is of particular interest, the segment shown in the right image is following in detail analyzed.
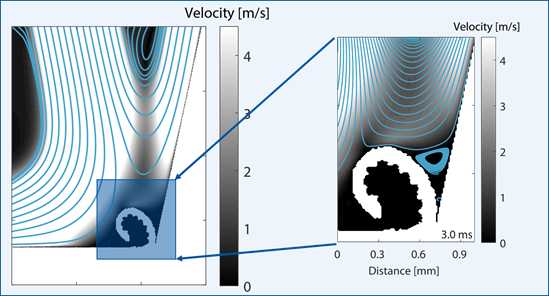
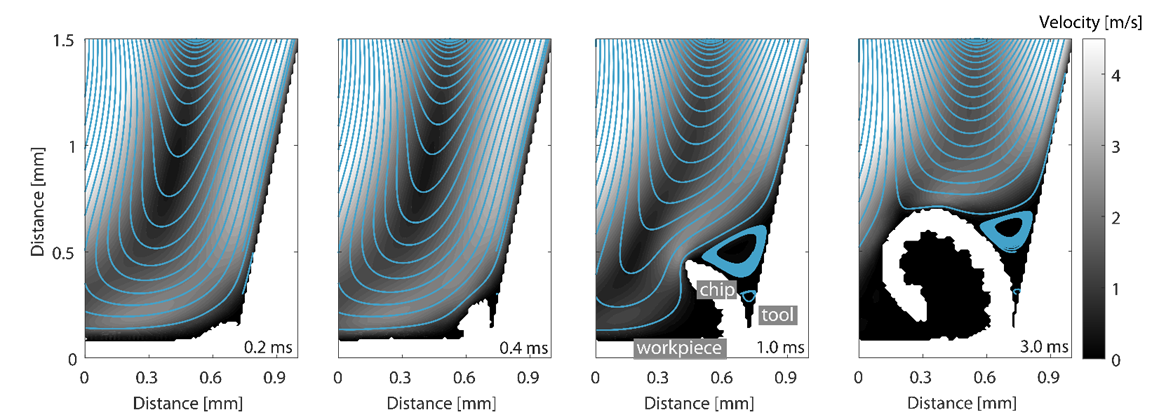
Therefore, Figure 5 shows the streamlines and velocity contour plot in the cutting zone for four different time steps. As the initial chip forms after 0.2 ms, the fluid flow is barely influenced by the chip geometry. The flow is rather redirected by the workpiece and attaches the tool surface already after a few tenths of millimeters remaining afterwards parallel to the tool surface. In the next larger geometry (0.4 ms), the growing chip shifts the streamlines upwards and constricts the flow from reaching the main cutting zone. With further increasing chip size (1.0 ms), the flow resistance becomes more dominant causing a significant redirection of the fluid near the chip. The fluid flow needs to circulate around the chip before reattaching the tool surface. Simultaneously, the recirculation zone above the tool-chip interface expands and induces an additional upward shift of the fluid. Accordingly, the flow reattaches at a height of 0.6-0.7 mm above the cutting zone. With ongoing chip evolution (3 ms), the location and size of the recirculation zone changes only slightly, revealing, however, a bit more horizontal orientation. Also, the flow reattaches approximately at the same location as in the previously discussed geometry. It should be considered that the current 2-dimensional simulation domain supports the establishment of stagnation zones, as no fluid can exit the domain to the front and back. Therefore, future studies will focus on the flow field of a 3-dimensional geometry.
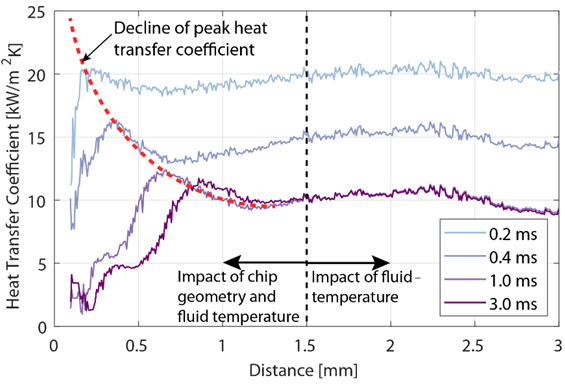
After the flow field analysis, Figure 6 shows spatial trends in heat transfer coefficients along the tool surface for the previously discussed time steps. Two major features are observed here: First, the chip evolution causes a shift in convective heat transfer coefficient. Starting at a distance of 0.2 mm to the tool tip, the peak is displaced up to 0.8 mm for progressing chip evolution. The majority of the displacement occurs approximately during the first third of the chip evolution (< 1.0 ms) and reveals afterwards only minor variations. This coincides well with the observations made in Figure 5, where after 1 ms only minor changes in the recirculation zone are found. Second, the heat transfer coefficient reveals a general decrease along the entire tool surface with progressing time. This is particularly noticeable at the beginning and becomes less dominant at later times. Between 1 and 3 ms, changes in heat transfer coefficient are barely noticeable. An explanation for this phenomenon is the preheating of the cooling lubricant as it passes the evolving hot chip. This causes a reduced temperature difference at the following tool interface and therefore manifests in a lower heat transfer coefficient. At the beginning of the simulation time, the chip covers only a small part of the cutting zone causing only minor preheating of the fluid. Then with growing volume, the contact area between fluid and chip increases which in turn causes additional preheating of the fluid. The described phenomena are also highlighted with the black dotted horizontal line in Figure 6 which marks the transition between two heat transfer regimes. To the left, the heat transfer coefficient is influenced by the evolving chip geometry as well as the increasing contact time with the hot chip. In contrast at the right side, the chip evolution does not impact the general behaviour in heat transfer coefficients, rather the coefficients reveal a self-similar trend, differing only by a constant offset. Particularly interesting here: The trends extracted at later times (1.0 and 3.0 ms) do not show any difference.
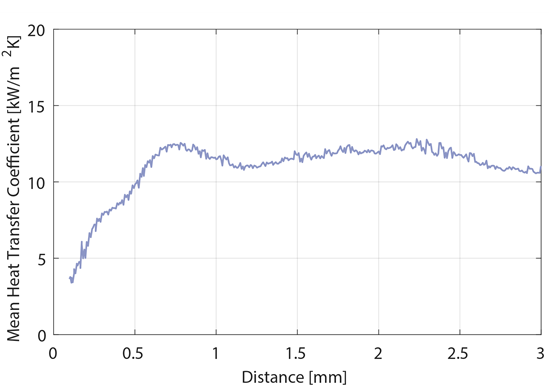
Following, Figure 7 shows the time-averaged heat transfer coefficient along the tool surface for an entire chip evolution (0 ms to 3 ms). The mean value shows first an increase in heat transfer coefficient and reaches a plateau at approximately 0.7 mm distance to the tool tip. Afterwards, only minor changes and as a more constant trend in heat transfer coefficient between 11 to 12 kW/m²K is observed. In general, the time-averaged values show a very similar pattern compared to the curves from later chip evolution time steps. This effect arises mainly due to the fast decrease in heat transfer coefficient at the beginning of the chip evolution. As shown in Figure 6, already after 1 ms, a major decrease in heat transfer took place. For the last two thirds of the chip evolution chip time, no significant variations occur. Therefore, the mean value orientates towards the results of the last two thirds of chip evolution.
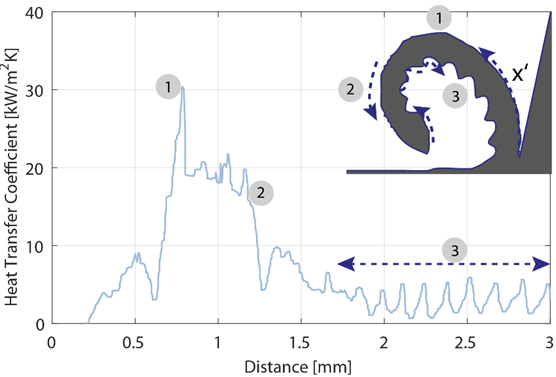
Besides the evaluation of heat transfer along the tool-lubricant interface, Figure 8 gives a first analysis of convective cooling along the chip surface for a progressed chip evolution (3 ms). For this purpose, the coordinate x’ is introduced to highlight the local coordinate system parallel to the contour of the chip. Basically, three different phenomena are observed and denoted with markers 1-3. The first marker is placed at the global maximum of the heat transfer coefficient where the lubricant jet impinges the chip surface and splits towards outlet and tool surface. Moving on to the second marker, the heat transfer coefficient decreases fast as the major flow direction is perpendicular away from the chip contour which is confirmed by the streamlines shown in Figure 5. After the second marker, the heat transfer coefficient declines further and remains in an interval between 2-6 kW/m²K. Moreover, the topography at the chip downside causes an oscillation in heat transfer coefficient (region 3). The local minima in this region correspond to ripple contours at the inner side of the chip. Concluding, as the CFD results show significant local variations in heat transfer, the influence of local chip temperature and development should be investigated in future mechanical chip formation simulations.
5. Conclusion
This paper investigates the impact of evolving chip geometry on the local heat transfer coefficient during orthogonal cutting. Precalculated, FEM simulations are used to determine the chip geometry which are used as input for the CFD simulation. Geometries and temperature fields for different chip development states are analysed and compared. It is shown that the chip geometry impacts the slope and form of the heat transfer coefficient profiles up to a distance of 1.5mm to the cutting edge. More upstream, all investigated trends have a self-similar profile only differing by a constant offset. Therefore, the heat transfer phenomenon is subdivided into two regimes: The near cutting-edge heat transfer, influenced by the fluid temperature as well as the chip geometry, and the upstream heat transfer which is only sensitive to the fluid temperature.
Acknowledgements
The authors T. Helmig and H. Liu would like to thank the German Research Foundation (DFG) for the funding the SFB/Transregio 96 collaborative research (Project ID 174223256-TRR 96) subproject A02 and B02. For T. Göttlich the funding by Deutsche Forschungsgemeinschaft (DFG, German Research Foundation) priority program SPP 2231 FluSimPro (Project ID 422633203) is greatfully acknowledged.
References
[1] Mayr J, Jedrzejewski J, Uhlmann E, Donmez M A, Knapp W, Härtig F, Wendt K, Moriwaki T, Shore P, Schmitt R, et al. 2012 Thermal issues in machine tools CIRP Annals. 61 771 - 791 View Article
[2] Yuan J, Lyu B, Hang W and Deng Q, 2017 Review on the progress of ultra-precision machining technologies Frontiers of mechanical engineering. 12 158 - 180 L. Stein, "Random patterns," in Computers and You, J. S. Brake, Ed. New York: Wiley, 1994, pp. 55-70. View Article
[3] Klocke, F. (2018). Fertigungsverfahren 1: Zerspanung mit geometrisch bestimmter Schneide. Springer-Verlag. View Article
[4] Chagas, G. M. P., Barbosa, P. A., Barbosa, C. A., & Machado, I. F. (2013). Thermal analysis of the chip formation in austenitic stainless steel. Procedia Cirp, 8, 293-298. View Article
[5] Çolak, O., 2012, "Investigation on Machining Performance of Inconel 718 in High Pressure Cooling Conditions," J. Mech. Eng., 58(11), pp. 683-690. View Article
[6] Courbon, C., Kramar, D., Krajnik, P., Pusavec, F., Rech, J., and Kopac, J., 2009, Investigation of Machining Performance in High-Pressure Jet Assisted Turning of Inconel 718: An Experimental Study, Int. J. Mach. Tools. Manuf., 49(14), pp. 1114-1125 View Article
[7] Baumann, A., Oezkaya, E., Schnabel, D., Biermann, D., & Eberhard, P. (2021). Cutting-fluid flow with chip evacuation during deep-hole drilling with twist drills. European Journal of Mechanics-B/Fluids, 89, 473-484. View Article
[8] Oezkaya, E., Iovkov, I., & Biermann, D. (2019). Fluid structure interaction (FSI) modelling of deep hole twist drilling with internal cutting fluid supply. CIRP Annals, 68(1), 81-84. View Article
[9] Oezkaya, E., Bücker, M., & Biermann, D. (2020). Simulative analyses focused on the changes in cutting fluid supply of twist drills with a modified flank face geometry. International Journal of Mechanical Sciences, 180, 105650. View Article
[10] Helmig, T., Peng, B., Ehrenpreis, C., Augspurger, T., Frekers, Y., Kneer, R., & Bergs, T. (2019). A Coupling Approach Combining Computational Fluid Dynamics and Finite Element Method to Predict Cutting Fluid Effects Tool Temperature in Cutting Processes. Journal of Manufacturing Science and Engineering, 141(10). View Article
[11] Liu H., Helmig T., Augspurger T., Nhat. N., Kneer R. & Bergs T. (2021) Modeling the Cooling Effect of the Cutting Fluid in Machining Using a Coupled FE-CFD Simulation. 2nd International Conference on Thermal Issues in Machine Tools. DOI: 10.17973/MMSJ.2021_07_2021062 View Article
[12] Ducobu, F., Rivière-Lorphèvre, E., Filippi, E. Application of the Coupled Eulerian-Lagrangian (CEL) method to the modeling of orthogonal cutting. Eur. J. Mech. A/Solids 2016, 59, 58-66. View Article
[13] Puls, H., Klocke, F., Veselovac, D. FEM-based prediction of heat partition in dry metal cutting of AISI 1045. Int. J. Adv. Manuf. Technol. 2016, 86, 737-745. View Article
[14] Puls, H., Klocke F, Lung D. Experimental investigation on friction under metal cutting conditions. In: Wear. 2014, vol. 310, pp. 63-71 View Article
[15] Seimann, M., Peng B. X., Fischersworring-Bunk, A., Rauch, S., Klocke, F., Model-based analysis in finish broaching of Inconel 718. In: The International

