Journal of Fluid Flow, Heat and Mass Transfer (JFFHMT)

ISSN: 2368-6111

Application of DLVO Modeling to Predict Critical pH for Fines Migration Pre- and Post-SiO2 and MgO Nanofluid Treatments in Sandstones

Rizwan Muneer¹, Peyman Pourafshary¹, Muhammad Rehan Hashmet²

¹Nazarbayev University, Department of Petroleum Engineering
53 Kabanbay Batyr Avenue, Nur-Sultan, Kazakhstan, 010000
rizwan.muneer@nu.edu.kz; peyman.pourafshary@nu.edu.kz
²United Arab Emirates University, Chemical and Petroleum Department
Sheik Khalifa Bin Zayed Street, Asharij - Abu Dhabi - United Arab Emirates
mrhashmet@uaeu.ac.ae

Abstract - Injection water pH affects the release of fines in sandstones. The force equilibrium between fines and sand governs the attachment or release of fines in the system. At a pH higher than a critical value, fines are released and block the pores, causing formation damage. The fines release can be avoided by adjusting the pH and using nanofluids. This paper introduces the concept of DLVO modeling to estimate the critical pH before and after the application of nanofluids without extensive experimentation. Scanning electron microscopy determines the average size of in-situ fines collected from the sandstone core. Injection brine of 11700 ppm and 0.1 wt% SiO₂ nanofluid are prepared, the zeta potentials of dispersed sand are measured with varying pH from 2 to 12, and the resulting attractive and repulsive surface forces between fines and sand grains are quantified. The DLVO models are developed to predict the mobilization of fines and a critical pH before and after the application of silica nanofluid. The zeta potentials are measured by a Zetasizer and are in the range of -5 mV (less repulsion) to -31 mV (more repulsion). Furthermore, the application of nanofluids increases the zeta potential to a range of -3 mV to -24.9 mV, indicating a compression in electric double layers. Measured zeta potentials, ionic strength, and fine size are used as inputs to compute surface forces, and DLVO models are developed. The critical pH, at which total DLVO interactions shift from negative to positive, as predicted by the model, is about 8. A separate DLVO model predicted an improved critical pH of 11 following the use of SiO₂ nanofluid, demonstrating a reduction in repulsion forces. Furthermore, the DLVO model estimated a critical pH of 12 after using 0.0075 wt% MgO nanofluid, demonstrating the greater efficiency of MgO nanoparticles even at low concentrations. DLVO modeling approach gives a new insight into predicting critical pH before and after applying nanofluids, and nanotechnology validates the ability of nanoparticles to control fines migration and improve critical pH for waterflooding and alkaline flooding operations.

Keywords: Sandstone, Formation damage, Fines migration, Nanoparticles, Zeta potential, DLVO modeling, pH.

© Copyright 2022 Authors - This is an Open Access article published under the Creative Commons Attribution License terms Creative Commons Attribution License terms. Unrestricted use, distribution, and reproduction in any medium are permitted, provided the original work is properly cited.

Date Received: 2022-09-19
Date Accepted: 2022-09-28
Date Published: 2022-10-13

1. Introduction

Oil-containing sandstone reservoirs are a significant contributor to global energy and account for approximately 60% of the world's petroleum reservoirs [1]. Sandstone reservoirs contain ultra-fine quartz and clay particles attached to the sand surface, and this attachment creates a sand-fine-brine (SFB) system [2]. Clay minerals, such as kaolinite, illite, montmorillonite, and chlorite, are the ones that have the broadest distribution and are responsible for the generation of the most migrating fines [3], [4]. The electrostatic force of attraction and gravitational force both hold fine particles to the rock surface. The electric double layers (EDLs) around fine particles and sand grains are compressed in the given sand-fine- system due to the high charge density, maintaining an equilibrium between fine particles and sand grains in high salinity formation water (FW) [5].

In an environment with a high salinity formation of water, there are electrostatic forces of van der Waals attraction (V_LVW), electric double layer repulsion (V_EDL), and weak Born repulsion (V_Born) between fine particles and sand grains. Fine particles are affixed to the sand's surface by the overall attractive interaction energy of the SFB system. Fine particles remain attached to sand grains mainly due to the van der Waals force, and the strength of this force is proportional to the fine particle size as well as the distance from the surface of the sand that separates them. The electric double layer repulsion force, on the other hand, tends to detach fine particles from the rock surface, and the zeta potential of the SFB system is the primary factor that determines the strength of this potential [6]. Derjaguin, Landau, Verwey, and Overbeek (DLVO) proposed a theory based on surface force quantification and analysis that can be used to model the dynamic behavior of a sand-fine-brine system and investigate the effect of various crucial factors on fine migration initiation [7]–[9]. Equation 1 illustrates the DLVO-based total potential (V_Total) of a system that consists of a fine particle and a sand grain surface. This equation represents a summation of all the energies that are present in the SFB system.

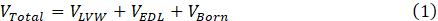
Where V_Total is the total interaction potential of the sand-fine-brine system, V_LVW denotes van der Waals attraction potential, V_EDL presents electric double layer repulsion potential and,  V_Born is Born repulsion potential. Fines migration is triggered by variations in attractive and repulsive surface forces induced by the incursion of freshwater into underground formations, mud invasion during drilling operations, completion fluid use, acidizing cleaning, and water injection during secondary and tertiary recovery operations [10]–[13]. Fines can be released and migrate under certain conditions, and their movement can be predicted as a function of the injected brine's salinity, ionic strength, flow rate, pH, and presence of monovalent and divalent ions, as well as the concentration of in-situ fines and temperature. Because of low salinity waterflooding, as the SFB system salinity decreases due to the injection of low salinity water, electric double layers around fines and sand grains expand, and fine particles are dislodged due to high repulsion forces, and migration begins inside the reservoir even at low flow rates. Detached and migrating fines might plug pore throats, causing productivity and injectivity issues and a high-pressure drop in the system [14]–[16].

The pH of the SFB system may rise after water injection due to the solubilization and dissolution of rock minerals such as calcite and siderite. This has a considerable impact, particularly in the process of water flooding, on the release of fine particles in sandstones above a specific pH value called a critical pH. The release of fines because of an increase in the system pH can be attributed to an increase in the repulsive forces and modeled using the DLVO approach [17], [18].

In our previous studies, DLVO models were developed, and critical salt concentrations were estimated based on the characterization of surface forces between fines and sand grains under low salinity water injection with monovalent and divalent ions [6], [19]–[21]. The application of silica nanoparticles in the form of nanofluid provides promising results in controlling fines migration and reducing the critical salt concentration. The DLVO models also incorporated the effects of silica nanoparticles, and all model results were validated experimentally. The current research provides a new insight into the estimation of a critical pH using the DLVO modeling technique and incorporates the effect of different concentrations of SiO₂ and MgO nanoparticles in the model to mitigate fines migration and improve the critical pH value.

2. Research Methodology

2. 1 Brines

In the experimental phase, high salinity formation water (FW) of 77000 ppm was prepared and used to saturate the sand grains to recreate sandstone reservoir conditions. NaCl brine of 11693 ppm with a pH range of 7-12 was used to determine the critical pH for the given sand-fine-brine system. The ionic compositions of the formation water and base brine are given in Table 1.

Table 1. Composition of formation water and NaCl brines.

Ions	FW (ppm)	0.2M NaCl (ppm)
Na+	23426	4600
Ca2+	4448	-
Mg2+	1300	-
Cl-	47781	7093
Total	76955	11693

2.2. SiO₂ Nanofluid Preparation

To investigate the effect of nanoparticles on critical pH value, Glantreo Ltd. Ireland provided silica nanoparticles of 20 nm size in the form of a 25 wt% concentrated solution. These nanoparticles were chosen because of their hydrophilicity, better stability, low toxicity, and superior performance in controlling fines migration in sandstone core samples. Furthermore, 0.1 wt% nanofluids were produced by diluting the dispersion with 0.2M NaCl brine.

2. 3. Zeta Potential Measurements

DLVO modeling requires sand-brine and sand-nanofluid zeta potentials as inputs. A sandstone core sample was crushed in a cone crusher and sieved to a 40-micrometer sand particle size for this purpose. To eliminate any contaminants on the sand grains, the sieved sample was washed with distilled water, HCl, acetone, and finally distilled water. With an ultrasonic homogenizer, the crushed sand particles were dispersed in brine and nanofluid, and the zeta potentials were evaluated with varied pH using Malvern Zetasizer (NanoZS) and a Titrator system.

2. 4. Characterization of Fine Particles

The sandstone core was used to collect the in-situ fines and scanning electron microscopy (SEM) was utilized to determine the morphology and average size of the fine particles. In addition, SEM-EDS (Energy Dispersive Spectroscopy), and x-ray powder diffraction (XRD) analyses were carried out to collect data on the chemical composition of fines.

2. 5. DLVO Modeling

The average size of fine particles, the ionic strength of the brine, and measured zeta potentials at different pH were utilized as inputs for DLVO modeling, and surface forces were computed using available methods indicated in our previous research [6]. The DLVO model was used to predict the critical pH, at which the total interaction energy shifted from negative to positive. The model was also utilized to test the effectiveness of silica nanofluid in changing surface forces and reducing fines migration even at higher pH levels.

3. Results and Discussion

3. 1. Zeta Potential Results

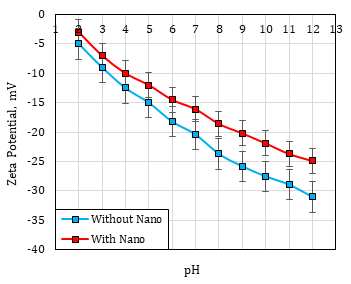
Zeta potentials of dispersed sand particles were measured before and after the application of SiO2 nanofluid as shown in Figure 1. As the pH of the solution increases, the electric double layer expands, and the corresponding zeta potential decreases. On the other hand, the application of silica nanoparticles decreases the expansion of the electric double layer and increases zeta potential.

3. 2. Fines Characterization

SEM and SEM-EDS were used to examine the collected fines. The fine particles were mostly kaolinite clay (Al₂Si₂O₅(OH)₄), according to SEM-EDS and XRD, as shown in Figure 2., and their average size was around 800-900 nm

3. 3. Critical pH by DLVO Modeling

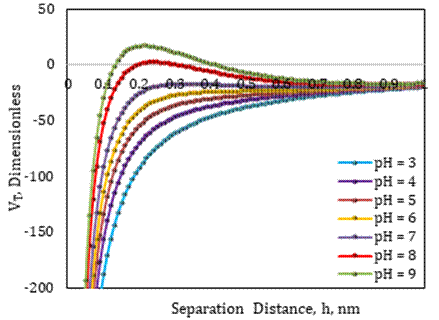
Surface forces between fine and sand grain were estimated using observed zeta potentials under various pH conditions without nanoparticles, brine ionic strength, and average fine particle size, and then the total interaction energy of each system was determined using DLVO modeling, as shown in Figure 2. Using the models presented in our earlier study, surface forces are determined [6]. The sum of attraction and repulsion potentials is the total interaction energy of the system under consideration. Because of compacted electric double layers around fines and sand grains in a low pH environment, such as a pH=3 solution, forces of attraction dominate repulsion forces, and the total energy is negative, indicating that there will be no fines migration in the system. The same findings were achieved for the total interaction energy in the negative region for pH 4-7 environments. However, for brine of pH=8, the total interaction energy shifted from negative to positive indicating the dominance of repulsive forces in the system at a separation distance of around 0.25 nm. This can be attributed to the expansion of electric double layers around fines and sand grains under high pH conditions. Based on the DLVO model results, pH 8 was predicted to be the critical pH, and fines migration in the sand-fine-brine system may occur at or above this value.

3. 4. Effect of SiO₂ Nanofluid on Critical pH

The surface forces between fines and sand grains were quantified using zeta potentials under different pH conditions with the utilization of 0.1 wt% SiO₂ nanofluid, brine ionic strength, and average fine particle size, and the total interaction energy of each system was calculated using DLVO modeling, as shown in Figure 3. By altering the surface charge of sand grains, silica nanoparticles assisted to limit the expansion of electric double layers in high pH environments. Forces of attraction dominate repulsion forces in the presence of compacted electric double layers around fines and sand grains in the pH range of 6-10, and the total energy is negative without any fines migration in the system. The overall interaction energy shifted from negative to positive for brine with pH=11, suggesting the dominance of repulsive forces in the system. This occurs because of nanoparticles’ adsorption on the surface of the sand grains, which causes the electric double layers to contract even under higher pH values. The results of the DLVO model indicated that pH 11 would be the new critical pH, and it was projected that fines migration in the SFB system would take place at this value or higher after the application of SiO₂ nanofluid.

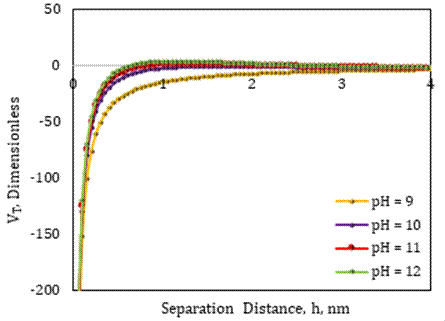
3. 5. Effect of MgO Nanofluid on Critical pH

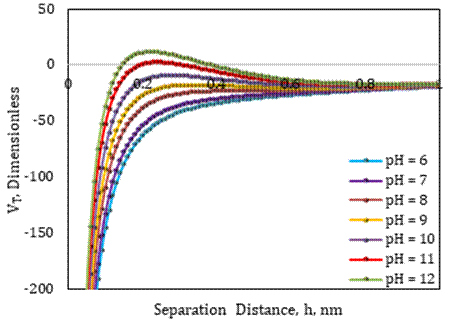
The zeta potential data for 0.0075 wt% MgO nanofluid with various pH values were gathered from the literature [17] in order to predict critical pH and compare it to the case of SiO2 nanofluid. The surface forces between fines and sand grains were measured using zeta potentials at various pH levels with MgO nanofluid, brine ionic strength, and average fine particle size, and the total interaction energy of each system was computed using DLVO modeling, as shown in Figure 4. It is noticeable that forces of attraction outweigh forces of repulsion when compacted electric double layers are present surrounding fines and sand grains in the pH range of 9 to 11, and the total energy remains negative with no fines migration in the system. However, for brine with pH=12, the total interaction energy changed from negative to positive, indicating that repulsive forces dominated the system. As predicted, fines migration in the SFB system would occur at pH 12 or higher after the application of 0.0075 wt% MgO nanofluid, according to the results of the presented DLVO model.

4. Accuracy of DLVO Model

The application of DLVO modeling based on surface force analysis to predict fines migration in porous media has proven to be an accurate approach provided that the sand-fine-brine system is defined correctly, and all the apparatuses work perfectly for precise measurements. The accuracy of the DLVO model and its predictions depend on the accuracy of the measured zeta potentials of the sand-fine-brine system, injection brine salinity and pH, and average size fine particles. For this purpose, sand-fine-brine dispersions were prepared following the standard procedure and zeta potentials were measured using Malvern Zetasizer Nano ZS. To ensure the accuracy of the data, three measurements were made for each dispersion, and the DLVO model used the average value of zeta potential. Brines of desired salinity were prepared using pure chemicals from Sigma-Aldrich according to the standard procedure, and the salinity was tested using a salinity meter. A high-precision Zeiss 540 crossbeam scanning electron microscope was used to determine the average fine particle size. These precisely measured parameters were employed in DLVO modeling to reduce error and obtain accurate predictions. Furthermore, in our previous research, all the developed models were experimentally validated, and the results were within an acceptable error range of 10%. Table 2 shows a comparison between DLVO model predictions and experimental results.

Table 2. Validation and accuracy of DLVO modeling

DLVO model predictions	experimental results	difference
CSC of 0.11M NaCl in Berea sandstone core.	CSC was 0.1M NaCl [21]	0.01M NaCl
CSCs of 0.085M and 0.075M NaCl for 0.05 wt% and 0.1 wt% concentrations of silica nanoparticles, respectively.	CSCs were 0.08M and 0.07M NaCl for 0.05 wt% and 0.1 wt% SiO2 nanofluids, respectively [21]	0.005M NaCl
CSC of 0.044M KCl in Berea sandstone core.	Experimental CSC was 0.04M KCl [20]	0.004M KCl

The comparison in Table 2 shows that the DLVO modeling approach can accurately predict crucial parameters if all key parameters such as zeta potential, fine particle size, brine salinity, and pH are measured accurately. Otherwise, an inaccuracy in one parameter might lead to error propagation, resulting in erroneous DLVO model predictions.

5. Conclusions

During waterflooding and alkaline flooding operations, estimating the critical pH of injection water is a crucial factor to prevent formation damage due to fines detachment and migration. The DLVO modeling approach, which is based on the quantification and analysis of surface forces, is a useful tool for analyzing fines migration and control in sandstones during alkaline flooding without having to conduct major experiments. The following is a summary of the results:

• A critical pH for a sand-fine-brine system was predicted using the DLVO modeling technique before and after the application of nanofluids.
• The DLVO model predicted a critical pH of 8 at which the total interaction energy of the SFB system moved from negative to positive, indicating the dominance of repulsion forces in the system.
• In addition, after the application of 0.1 wt% SiO2 nanofluid, the DLVO model predicted a new critical pH of 11.
• In comparison to 0.1 wt% SiO2 nanofluid, the DLVO model predicted a new critical pH of 12 after the application of 0.0075 wt% MgO nanofluid.
• Even at extremely low concentrations, MgO nanofluid application was shown to be more effective than SiO2 nanofluid application.
• An increased critical pH value indicates the effectiveness of nanoparticles in form of nanofluids in controlling fines migration and avoiding formation damage even at a higher pH during alkaline flooding operations.

Acknowledgments

The authors would like to thank Nazarbayev University for supporting this research through the NU Faculty Development Competitive Research Grants program (Application of Nanofluids to Control Formation Damage and Improved Oil Recovery Process, Code: 240919FD3928).

References