Journal of Fluid Flow, Heat and Mass Transfer (JFFHMT)

ISSN: 2368-6111

1. Introduction

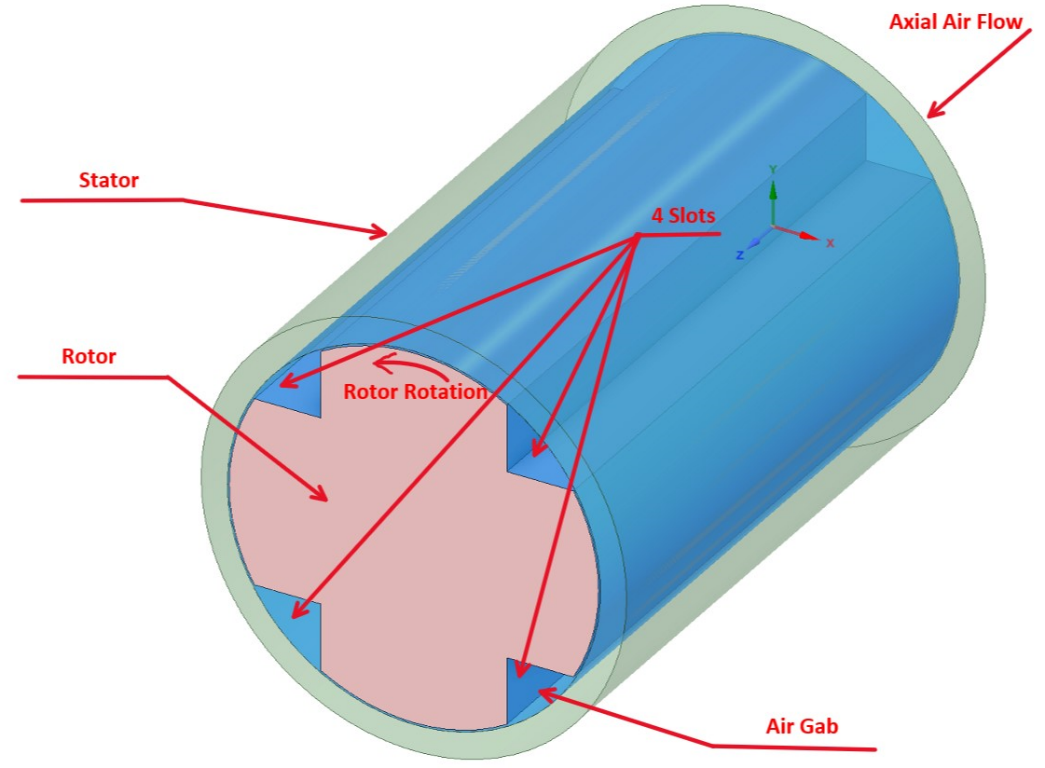
Any electrical motor generates heat from the losses inside its electric windage. Hence, electric motors require proper cooling to avoid overheating. The cooling of a synchronous electric motor can be achieved by passing an axial air flow through the slotted gap between the rotor and the stator. Figure 1 shows the shape and location of such gab in a four-pole electrical motor. The flow rate of the axial air flow required to provide sufficient cooling depends on the rotational speed. Hence, the effect of the rotational speed and the rate of axial air flow on the rate of heat transfer inside the motor gap must be investigated.

2. Literature Review

Cooling of electric motors has been studied by many researchers as it is very critical in electric motors operation. Studies like [1-4] focused on the fluid flow and heat transfer of the Taylor-Couette flow inside electric motors, which represents flow between two concentric cylinders without an axial flow.

A review of flow between concentric cylinders was carried out by [5]. The review covered the presence of an axial flow with the Taylor-Couette flow. The problem of interest which involves a Taylor-Couette flow with an axial flow has been referred to as the Taylor-Couette-Poiseuille flow. The Taylor-Couette flow might experience flow instabilities, especially if the inner cylinder is rotating at high speeds while the outer cylinder is fixed. [6] investigated Taylor-Couette flow instabilities.

Other authors studied Taylor-Couette flow (TCF) considering various configurations. [7] considered a multiphase TCF. [8] studied TCF in a narrow spherical gap. [9] considered TCF in a wider gap. [10] considered a laminar-and turbulent TCF. [11] considered a highly turbulent TCF. [12] studied a TCF between two concentric cylinders while the inner cylinder is having ribs. [13] investigated heat transfer characteristics of a TCF in a gap while the outer cylinder has a set of axially distributed slits.

[14] studied the effect of the gab entrance region on TCF with inner rotating cylinder and fixed outer cylinder. They showed that the entrance region in their case is similar to the entrance region of a pipe or a duct. [15] added a set of slots to the motor stator and investigated their effect on the rate of heat transfer of the flow within the annular gap. They showed that these slots have almost no effect on the rate of heat transfer.

To the best of the authors’ knowledge, there has not been any studies that considered the effect of axial flow within a slotted rotor under operating conditions leading to a high rotational Reynolds number reaching 27000. These conditions are of prime interest in real practical applications.

3. Problem Definition

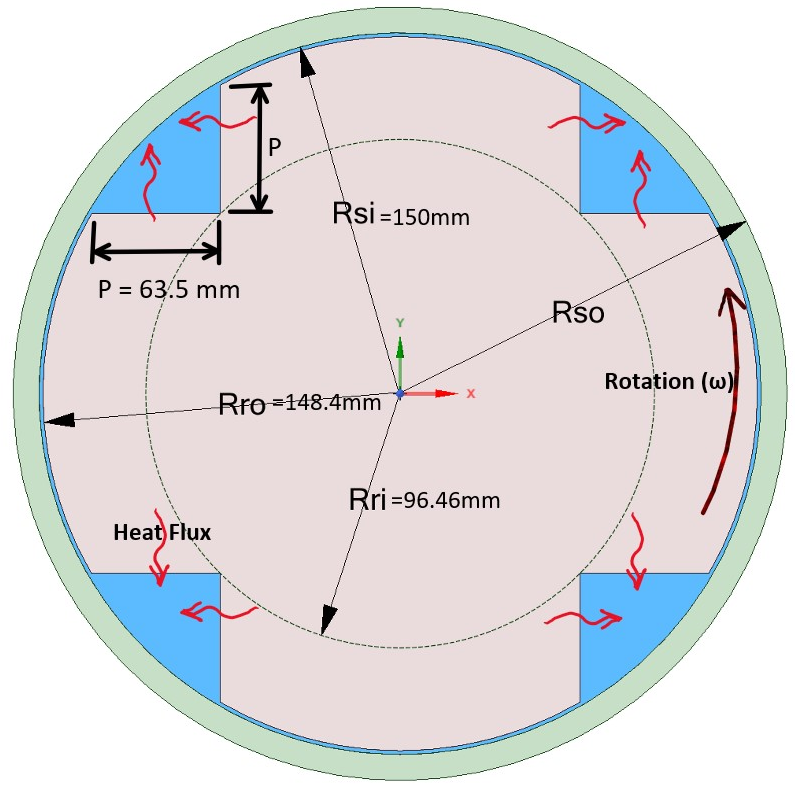
The problem of interest involves the cooling of a synchronous 4-pole electric motor using an axial air flow passing inside the gap between the rotor and the stator. The study resolves the flow and thermal fields inside the annular gap in the presence of the axial air flow through the rotor slots, as shown in Figure 2.

The inner rotating cylinder (i.e., the rotor) is subjected to a uniform heat flux of 500 W/m², which is the amount of heat generated due to electric losses within the motor windage. The outer cylinder (i.e., the stator) is assumed here as an insulated surface, hence no heat is being transferred to the surrounding air. All the walls were assumed smooth. Thermal radiation has been neglected. The radius ratio, (Rri/Rro), of the considered configuration is 0.65, which is similar to commercial synchronous motor available in market. The length of the rotor is 0.5 m.

4. Mathematical Model

The fluid flow and heat transfer problem has been simulated using ANSYS-CFX 2021 R1 commercial package. All the governing equations including mass, momentum and energy equations have been solved as referenced in [16].

The turbulence model used in this work is the Shear Stress Transport (SST) turbulence model to resolve the turbulence in the moving air flow. The SST turbulence model was chosen also in order to resolve the turbulent flow near the walls. The grid used in the current simulations has 106 elements. A grid dependence test has been carried out and the current grid has been selected so that the numerical results do not depend on the number of elements within 2%.

The boundary conditions are: at the insulated fixed stator, a zero heat flux is used. At the rotor: a fixed rotating speed (ω) is assumed. Its value was varied according to the value of the rotational Reynolds number (Re_r) considered in each simulation. The rotor surface was assumed smooth and subjected to a constant uniformly distributed heat flux of 500 W/m².

The air velocity at the entrance is constant and its value corresponds to the value of the axial Reynolds number (Re_a). Entering air temperature is assumed 25℃. At the exit: air pressure is equal to the atmospheric pressure.

The definitions of the axial Reynolds number (Re_a), the rotational Reynolds number (Re_r), the Nusselt number (Nu) and the hydraulic diameter (D_h) are provided in the following equations:

(1)

(2)

(3)

(4)

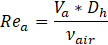
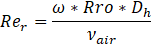
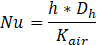
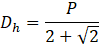
The axial velocity (V_a) is assumed equal to the average air velocity through the slots at the entrance. The kinematic viscosity (ν_air) and the thermal conductivity (K_air) of the air are calculated at the average fluid temperature across the gap. The heat transfer coefficient of air inside the gab is referred to by (h). The angular velocity of the rotor is identified by (ω). Gab width (P) is defined as shown in Figure 2.

4. 1. Validation of the Numerical Results

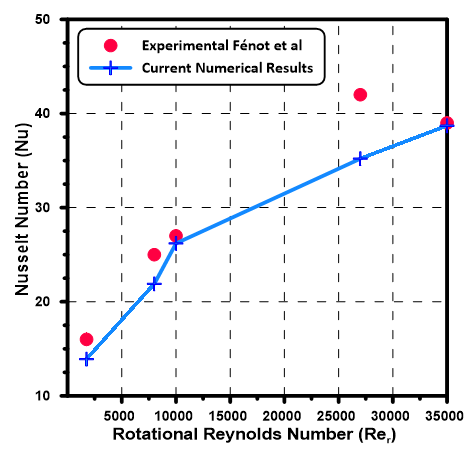
Validation of the current numerical results has been carried out using experimental results published in [17]. [17] considered heat transfer from an axial air flow inside a slotted rotor of a synchronous electrical motor.

The hydraulic diameter used in [17] was 15.8 mm, the radius ratio was kept fixed at 0.75 and the value of the axial Reynolds number was 4280. The value of the rotational Reynolds number was varied from 1750 to 10000. The heat generated inside the rotor is constant of 500 W/m². The maximum deviation between the present numerical results and the experimental data reported in [17] is about 16.8%, as illustrated in Figure 3.

5. Results and Discussions

The effect of the parameters investigated in the present study on the rate of heat transfer within the motor gap are: the rotational Reynolds number (Re_r) and the axial Reynolds number (Re_a) in the range of 1750 to 27000 and 2140 to 6425, respectively.

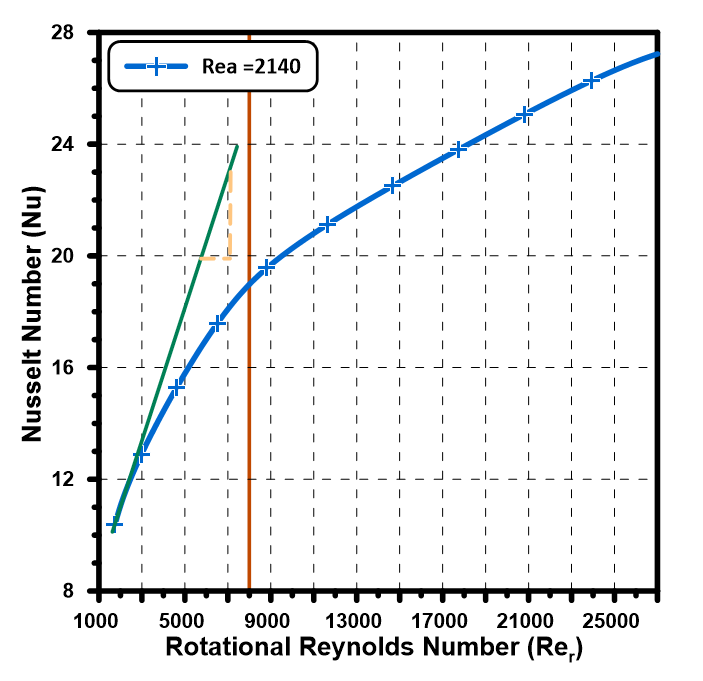
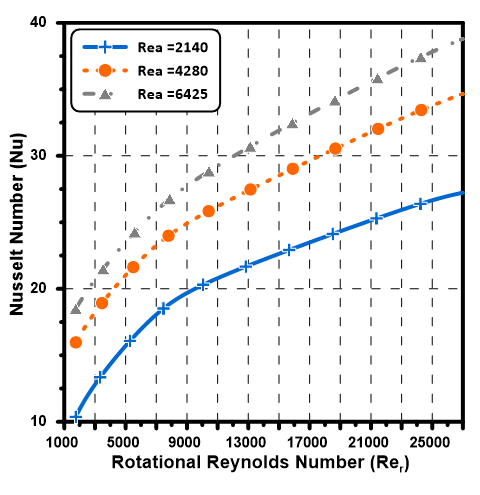
1. Effect of Re_r on Nu_av

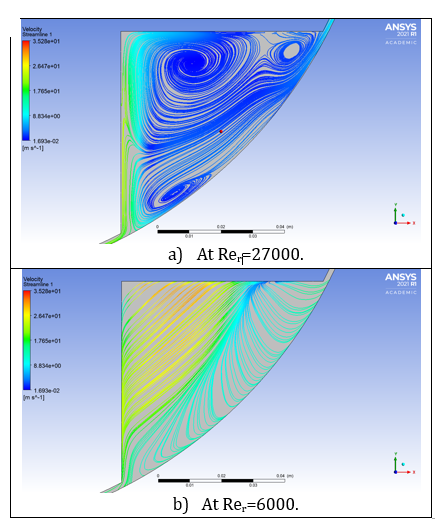
Figure 4 shows the effect of the rotational Reynolds number on the average Nusselt number inside the motor gap. The axial Reynolds number is kept constant at 2140. Results indicated that, increasing the rotational speed enhanced the rate of heat transfer within the gap. The results showed that the rate of increase in Nusselt number decreased somewhat at Re_r about 8000. The slope in Figure 4 at Re_r = 8000 has decreased by about 60% compared to the slope at Re_r = 1750 (Green Line in Figure 4). The rate of increase in Nusselt number decreased after Re_r = 8000 due to the increase in air circulation and the formation of large eddies inside the four longitudinal slots. Figure 5 shows the increase in air circulations and eddies inside one of the slots at Re_r=27000 compared to that at Re_r=6000.

5.2. Effect of Re_a on Nu_av

The effect of the axial and rotational Reynolds number on the average Nusselt number is shown in Figure 6. Increasing the axial Reynolds number (Re_a) from 2140 to 6425 resulted in an increase of the average Nusselt number inside the motor gap, at all values of Re_r considered in this study. Also increasing the rotational Reynolds number at any value of the axial Reynolds number resulted in improvement in the heat transfer inside the gap.

However, results showed that the effect of Re_a on the rate of heat transfer is more dominant than the effect of Re_r. Therefore, motor cooling is significantly improved by increasing the axial air velocity through the gap between the rotor and the stator. It is clear from Figure 6 that the rate of enhancement in Nu is reduced at Re_r equals to about 8000. Increasing Re_r above 8000 resulted in stronger eddies of hot air forming inside the gap (i.e., the slots), which decreased the rate of enhancement in Nusselt number, as shown in Figure 6.

5. Summary and Conclusions

The rate of cooling of a slotted electric motor using an axial air flow has been investigated numerically considering the effects of the rotational and the axial Reynolds numbers. Results showed that increasing the axial air flow or the motor rotational speed improves motor cooling. However, the effect of the axial air flow is more pronounced than the effect of the rotational speed. Results also showed that better cooling is achieved when the rotational speed corresponds to a rotational Reynolds number value below 8000, as the rate of enhancement in the average Nusselt number is decreased above this value.

6. Acknowledgement

The authors would like to acknowledge financial support of this work received from Mathematics of Information Technology and Complex Systems (Mitacs).

References