Journal of Fluid Flow, Heat and Mass Transfer (JFFHMT)

ISSN: 2368-6111

1. Introduction

Optimizing heat transfer through multilayer materials, for control of temperatures at associated surfaces, requires estimating the thermal response of layered composite materials, whose fabrication is both feasible and operationally practical. Accordingly, parametric models that combine heat transfer characteristics and thermal material properties, enabling prediction of temperature fields within multilayer materials and surface temperatures, should be well posed. These models should be conveniently adaptable for estimating the thermal response of different types of layered materials.

A general approach for control of heat transfer through multilayer materials is that of system design which includes heat sinks as embedded layers. This approach is motivated by welding processes, where work piece temperatures are controlled by thermal contact to base plates, and by electronic system designs requiring thermal management [1]. Parametric modeling of heat sink-controlled heat transfer can be based on linear combinations of numerical-analytical basis functions [1], whose mathematical foundation is that of Green’s functions and the inverse thermal analysis approach, where parametric models provide for inclusion of information concerning the physical characteristics of heat transfer processes. The present study concerns parametric modeling of a general system for layered configurations and heat sink-control heat transfer in layered materials and associated surface temperatures. This system is inherently multiscale in nature, and therefore poses a specific problem with respect to parametric modeling. For the purpose of parametric modeling, layered configuration and heat sink-controlled heat transfer in layered materials can be represented as occurring on different length scales. In addition, model parametrization includes effective diffusivities, which are based formally on replacing the advection-diffusion operator with an effective-diffusion operator, i.e.,

(1)

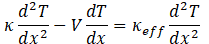
where V specifies the material flow field and κ_eff the effective diffusivity, which represents the combined influence of both thermal diffusion and advection. Physically, advection is not expected to manifest as influencing thermal transport locally within a layered material system, but rather as influencing thermal transport over an extended length. Accordingly, the phenomenological influence of advection, which is associated with ambient environments at surface boundaries of a layered material system, again poses a problem of inverse thermal analysis for determination of effective diffusivities. Finally, heat transfer along the heat sink layer is effectively singular because of the relatively large thermal diffusivity of this layer. Accordingly, with respect to parametric modeling, this layer can be represented by one having singular characteristics with respect to heat transfer. Heat transfer to the localized heat sink layer from adjacent layers of material will depend on the characteristic thermal coupling of layer interfaces, which again is a complex material property, not known a priori, and thus appropriately posed for inverse thermal analysis. The singular nature of heat sink coupling was demonstrated in reference [2-3].

In addition to providing quantitative estimation by means of inverse thermal analysis, parametric modeling can provide qualitative estimation of system response. For example, in the case of layer-configuration and heat sink-controlled heat transfer in layered materials, general design goals can be achieved by adjusting qualitatively relative locations and diffusivities of layers.

1.1. Model and Data Spaces

Following the inverse-problem approach for thermal analysis [4-9], a system is represented by a parametric model. The particular choice of a parametric model is termed a parameterization of the system. The choice of a particular parameterization, however, is in general not unique. To address the non-uniqueness of system parameterization, inverse problem theory has adopted the concept of model space, where sub-regions of this space represent conceivable parametric models of the system [5]. Given a model space for a specific heat transfer system, quantitative inverse analysis is further enhanced by isolating model-space regions associated with parameterizations that are physically consistent, conveniently adjusted with respect to measurement, and sufficiently general in terms of mathematical representation. A physically consistent, conveniently adjustable and sufficiently general parameterization of heat transfer in layered materials is significant for the following reasons. First, temperature distributions calculated by inverse methods represent a mapping from data space into parameter space; therefore, it is preferable to adopt a parametric function representation whose form tends to minimize any bias resulting from its mathematical form. Second, a set of parameters associated with a physically consistent representations can in principle be used to extract relationships between parameters, which provide further insight related to physical characteristics. Third, control and optimization of heat transfer in layered materials for a specific application requires a quantitative assessment of process characteristics over a sufficient range of process parameter values. System identification for purposes of process control and optimization is only realizable using parametric representations that establish a correspondence between model and process parameters over a sufficiently wide range of values. Fourth, a sufficiently general parametric representation can be adjusted to include influences due to incomplete information concerning the system. Fifth, for heat transfer processes, i.e., heat transfer in layered materials in this study, the data space contains direct measurements of temperature field quantities and intermediate field quantities related to these quantities via an assumed physical relationship. Finally, specification of a given system parameterization that is complete in the sense that, in principle, it can be applied to the inverse analysis of all types of processes within a given class of applications is equivalent to the specification of a complete set of basis functions. As discussed previously [1], numerical-analytical basis functions that are constructed using the heat-kernel solution of the heat-conduction equation [10] should be complete in this sense.

Organization of subject areas presented are as follows. First, parametric models of temperature fields for layer and heat sink-controlled heat transfer in layered materials are presented. Second, prototype inverse analyses using parametric models are described. Finally, a discussion and conclusion are given.

2. Parametric Model

The parametric model presented in this section is a phenomenological generalization of the analytical solution to the heat conduction equation for heat transfer through a boundary between regions having different thermal properties [10]. These models are characterized by general parametric representations that can be further extended and modified.

The general physical characteristics of layer-configuration and heat sink-controlled heat transfer through layered materials, and IR radiance at their surfaces, provides foundation for a phenomenological parametric representation of influences on thermal response due to embedded heat sinks and discontinuous changes in thermal diffusivity at layer interfaces. Formally, these influences can be modeled as resulting from phenomenological effective diffusivities, which are associated with effective layers of finite, as well as zero, thickness. Contributions to the temperature field can be represented by effective diffusivities providing a phenomenological implicit representation of interface influences. The effective diffusivities and layers comprising the parametric model described here include equivalent phenomenological representations of complex interface structure and heat sink coupling.

For layer-configuration and heat sink-control of temperature fields within layered materials and of IR radiance at outer surfaces where influences of different layers are represented by effective diffusivities, parametric representation in terms of linear combinations of numerical-analytical basis functions is of the form

(2)

(3)

(4)

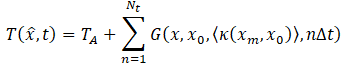
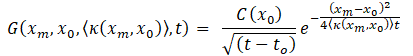
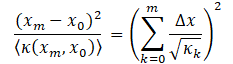
for x_m= m∆x, and

(5)

(6)

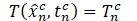
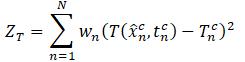
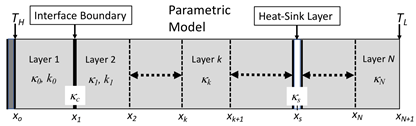
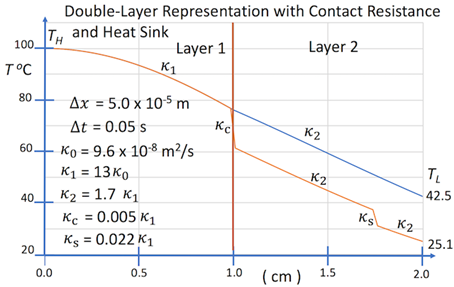
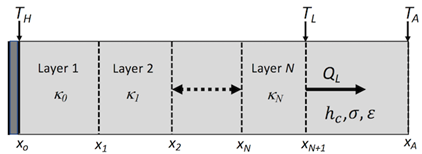
Equation (2) represents a linear combination of physically consistent and reasonably complete numerical-analytical basis functions for representation of the temperature field. The quantities C(x₀), k_k (k = 1-N), and are the equivalent source, effective diffusivities of the layered system, and time step for numerical integration to steady state [1]. The parametric model adopts these quantities as adjustable parameters for inverse thermal analysis and simulation of layer-configuration and heat sink-controlled heat transfer in layered materials. The quantity t₀ is an adjustable scaling parameter for weakening the singular character of basis functions with respect to time. The effective diffusivities comprising Eq. (4) are of three types, which are effective diffusivities representing heat transfer through layers, thermal contact resistance at interfaces of layers, and heat sink coupling. Shown in Figure 1 is a schematic representation of the parametric model.

For heat flow between two layers as shown in Figure 1, the steady-state heat flux Q_L is given by

(7)

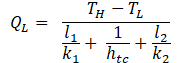
where k₁, l₁ and k₂, l₂ are thermal conductivities and lengths of layers 1 and 2, respectively, and h_tc is the thermal conductance coefficient of their interface. It should be noted that effective diffusivities in the parametric model, representing contact resistances, are equivalent to thermal conductance coefficients. The use of effective diffusivities to represent heat sink coupling is based on the observation that, although contact resistance and heat sink coupling are associated with different physical processes, their influences on heat transfer through a layered material are formally similar.

The locations and temperature values specify constraint conditions on the temperature field. Constraint conditions are imposed on the temperature field spanning the spatial domain of the layered material by minimization of the objective function defined by Eq. (6), where is the target temperature for position . The input of information into the parametric model is effected by the assignment of individual constraint values defined by Eq. (5) and form of the basis functions adopted for parametric representation, which include the influence of boundary and constraint conditions, i.e., T_H and T_L in Figure 1, and characteristic changes of thermal properties from one layer to another. The constraint conditions and parameterized basis functions provide for the inclusion of information from both laboratory and numerical experiments. The parametric model specifies a general procedure for parametric modelling of temperature fields in layered material systems. These parametric models are characterized by discrete numerical integration over time, where the time step ∆t is specified according to the average energy deposited during the time, for transition of the temperature field to steady state. Mathematical foundation of the parametric model is discrete representation of a parabolic partial differential equation, which is consistent with the physical characteristics of heat conduction, using a numerical integration procedure that is unconditionally stable [11].

3. Prototype Inverse Thermal Analyses

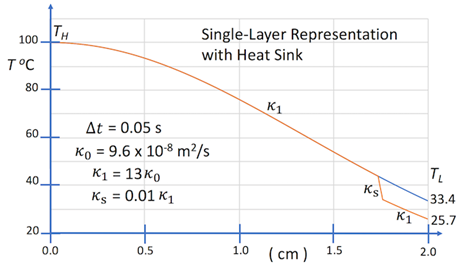
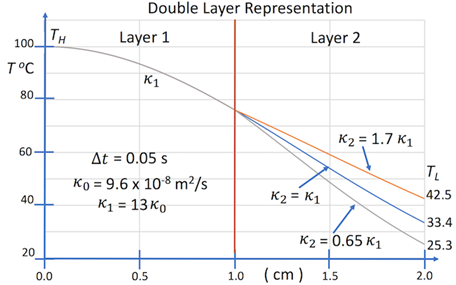
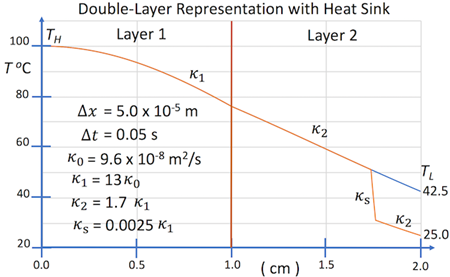
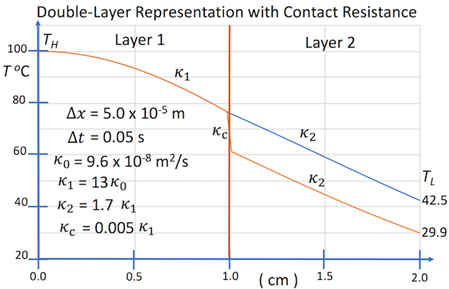
This section describes a series of computational experiments using parametric modelling of layer-configuration and heat sink-controlled thermal transport within layered material systems. The results of these computational experiments are shown in Figures 2-6. For these calculations, interface contact resistance and heat sink coupling were modelled using uniform distributions. The design of these experiments, which uses physically realistic thermal properties, was not for demonstrating optimal materials for layer-configuration and heat sink thermal control, but rather general characteristics of the parametric models for modelling and simulation, as well as demonstrating feasibly using multilayer and heat sink materials. The computational experiments described in this section represent both prototype inverse thermal analyses and simulations, which are both the goal of parametric modelling.

The inverse thermal problem as posed here assumes a complex interaction between a heating surface and multilayer material, as well as convective and radiative energy transfer at the outer surface of the multilayer material. For example, the interaction of a heating body and multilayer material can involve flow of material through porous microstructure within layers, and subsequent evaporation at the outer surface. A first estimate of the thermal response of a layered system using inverse analysis, without consideration of details concerning multilayer characteristics and heat sink-layer coupling, is determination of an effective diffusivity averaged over a single layer. For this type of thermal-response estimation the effective diffusivities k₁, k₂, and k₃ are assumed to be determined according to experimentally measured boundary values T_H and T_L, and an initial estimate k₀ (polypropylene) of the layer-material diffusivity without boundary and microstructural influences.

The simulation of heat transfer within complex layered material system, i.e., the direct problem of modelling heat transfer, assumes that a bounded parameter space of encoded thermal response, i.e., effective diffusivities, is available. This type of simulation is also described by Figure 1, where the effective diffusivities k₁,k₂, k_c, and k_s are assumed to be values within a parameter space, which is a complex function of process variables.

4. Discussion

Adopting the perspective of inverse thermal analysis, the parametric model presented here is part of a model space for parametric representation of data within a data space, which is defined as consisting of all possible temperature measurements associated with heat transfer through layered materials. Different parametric models within a model space and their associated parameterizations can represent different types of data, i.e., measurements and system characteristics as well as different types of details concerning these characteristics. The region of model space used for parametric representation, i.e., the specific parameterization used for inverse analysis, is based on the availability of information and assumed level of approximation for estimating thermal response of a layered material system. Accordingly, a specific parameterization selected within a model space is used to construct a parameter space for system characterization.

4.1. Control of Surface Temperatures

For the prototype inverse thermal analyses presented above, it was assumed that determination of effective diffusivities was according to experimentally measured boundary values T_H and T_L, as well as other assumed system characteristics. Another boundary value for inverse analysis is that of the heat-flux, Q_L, which depends on material properties of the outer surface and ambient environment (see Figure 8). In particular, Q_L equals the rate of heat transfer between the outer surface and ambient environment due to convection (advection and diffusion) and thermal radiation, and may be expressed by

(8)

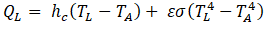
where h_c, ε , and σ are the convective heat transfer coefficient, emissivity of the outer surface (e.g., 0.97 for polypropylene), and Stefan-Boltzmann Constant (5.6704∙10^-8 W/(m²K⁴)), respectively, and T_A is the ambient temperature. The second term in Eq. (8) is the Stefan-Boltzmann-Law model of radiant heat [12]. For design optimization of layered material systems with respect to reducing surface temperature, one seeks to minimize the difference between T_L and T_A.

The prototype inverse thermal analyses adopts effective diffusivities and numerical-integration time step as independent adjustable parameters. This separation of parameters may provide some insight concerning the scaling of effective diffusivities relative to estimated bulk heat-transfer properties of materials comprising a layered system. Formally, however, an effective diffusivity, k_eff, and time step, ∆t, are not independent parameters, and can be combined phenomenological into a single adjustable parameter k_eff for inverse thermal analysis. In addition, the parametric model can provide representation of heat transfer through layered material system when effective diffusivities are functions of position within layers. This follows in that Eq. (4) can be adopted for approximate discrete representation of effective diffusivities whose forms are that of continuous functions.

General features of the parametric model were presented in this study with respect to both inverse thermal analysis and simulation. Given that a parameter space has been generated for a given system, a selected parametric model can be used for system simulation, and thus prediction of required parameters to achieve a given target temperature field. For example, the calculations shown in Figures 2-6 can be interpreted as prototype simulations of variations in material properties required to achieve a target surface temperature T_L, given that a parameter space of encoded thermal response properties is available. In principle, this parameter space would include effective diffusivities for different layered and heat sink materials for a sufficient range of boundary conditions.

As discussed in the introduction, heat transfer within the heat sink layer is that of a thin-layer material, interface-coupled to adjacent material surfaces. In general, experimental measurement and modelling of temperatures within this layer are for a temperature field spanning a two-dimensional surface, which is coupled to a cooling bath at specified locations along its edge. Development of parametric-model representations of this temperature field - which is on a different scale than that of heat transfer through a multilayer system - poses a separate problem, and is dependent on the system of interest.

The calculations shown in Figure 2-6 demonstrate inverse thermal analysis and simulation concerning general characteristics of layer-configuration and heat sink-controlled temperature fields within layered materials. These general characteristics provide foundation for a parametric model whose parameterization is phenomenological. These parameterizations can represent influences on thermal response due to complex interface characteristics, i.e., contact resistance.

5. Conclusion

Determination of optimal process parameters for achieving a given target temperature field for heat transfer through a layered material, and temperature at the layered-material surface using layer configurations and heat sinks poses a specific problem. The results of this study demonstrate general features of a parametric model, whose parameterization should provide convenient generation of parameter spaces for optimization of layered materials with respect to target heat transfer characteristics and surface-temperature reduction. This model consist of a general parametric representation that is structured for further extension and modification, which should be the focus of future studies. An important aspect of parametric models used for inverse analysis is parameter sensitivity. Further studies should investigate parameter sensitivity with respect to generation of parameter spaces for layer-configuration and heat sink-control of heat transfer and surface temperatures, using various types of layered materials.

References