Journal of Fluid Flow, Heat and Mass Transfer (JFFHMT)

ISSN: 2368-6111

1. Introduction

A The formation of soot and carbon black has been studied by several authors over the years and its for-mation mechanism still is an enigmatic subject. Many studies tried to understand and model the formation of soot, mainly for diesel engines [1]–[5], laminar/diffusion flames [6]–[8], and turbulent flames [9], [10]. Soot is a subproduct of combustion processes that arise from fuel-burning at high temperatures, being generated by incomplete combustion and aggregation of hydrocar-bons.

The formation mechanism of soot is directly relat-ed to the formation of polycyclic aromatic hydrocarbons (PAHs) by many authors. As described by Frenklach and Wang [11], PAHs are a combination of several aromatic rings, generating aggregates with high molecular weight. The authors describe this reaction mechanism by two processes, the addition reaction of two aromatic rings and its growth by the addition of vinyl (C2H3) and acety-lene (C2H2), which is named as HACA mechanism (hy-drogen-abstraction-C2H2-addition) [8], [11], [12]. After the polycyclic aromatics are formed there are a few steps to generate soot particles, described in the litera-ture as nucleation, superficial growth, and agglomera-tion [13]–[15]. By understanding these formation steps, it would be possible to mathematically model how soot is produced in combustion processes.

There is industrial interest in the production of carbon nanoparticles, but these particles are commonly divided into two categories: soot and carbon black. The former is a subproduct of combustion reactors, having a composition of 60% of pure carbon and, the latter is a purer form of soot, with compositions reaching 97% of elemental carbon [16]. Carbon black’s production is of particular interest, due to its diverse applications. This material is mainly used as a rubber reinforcement on tires, although they are also mixed with modern battery slurry to increase life and battery performance [17]–[19].

In this study, we propose to simulate the manufac-ture of carbon black using the Flame Spray Pyrolysis (FSP) process, which is in fact, similar to the most com-mon method of carbon black’s producing, named furnace black [20]. The main advantage of using the FSP process is that its controlled environment allows one to control specific characteristics of the generated particles [21]. Features like electrical conductivity, superficial area, and particle size are directly related to its manufacturing procedure. By controlling the FSP process parameters such as temperature, the air of co-flow, and fuel rate, it is possible to generate auspicious characteristics in the final product [22]–[26].

Flame spray pyrolysis is a well-known method for nanoparticle production and can manufacture particles of several elements from the periodic table. The process has important technological features such as the direct use of liquid feeds, proven scalability, and high-temperature flames and temperature gradients along the reactor [21]. The synthesized material’s properties are determined and controlled by operating conditions and nozzle configuration, which brings different possibilities to nanoparticle production. By coupling computational fluid dynamics (CFD) with populational balance model-ing (PBM) to describe particle dynamics, it is possible to simulate different conditions and predict relevant as-pects of the process and the particles produced [25]. In this work, we carry out simulations with ANSYS Fluent 19.2, aiming to simulate carbon black production in an FSP reactor using different approaches and reactor configurations.

2. Simulation Setup

The reactor system is approximated by a 2D ax-isymmetric domain, where the continuous gas phase is represented by an Eulerian framework, and the dis-persed evaporating droplets by a Lagrangian framework, with two-way coupling between phases. Steady-state and compressible flow conditions are considered, and turbulence is calculated with a k-ω SST model, as de-scribed in the works of Bianchi Neto, et al. [26].

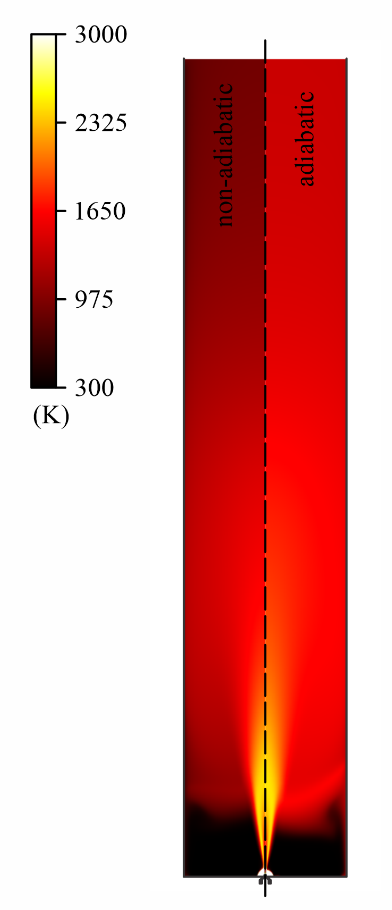
A numerical mesh, with approximately 200.000 hexahedral elements, is used in the discretization of the domain that consists of a cylindrical reactor (surrounded by a glass tube) with 500 mm of height and 100 mm of diameter, with a nozzle placed at the bottom, as shown in Figure 1. Two conditions at the tube wall were investigated. Firstly, an average convective coefficient of h = 25 W m^-2 K^-1 is proposed to simulate the heat transfer between the reactor and the outside environment, and secondly, the wall is considered adiabatic, to study the influence of thermal insulation on the reactor temperature and carbon black formation.

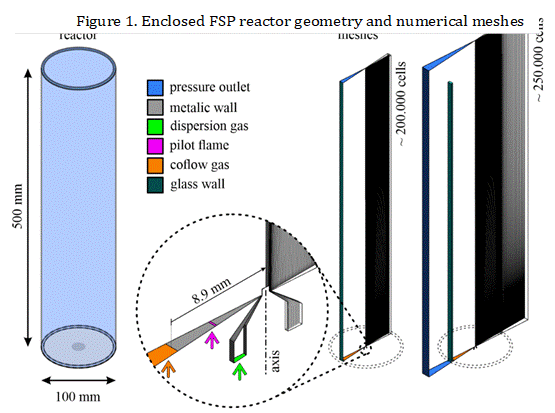
Furthermore, additional simulations were per-formed including the air surrounding the reactor, to veri-fy the adequacy of the proposed convective coefficient. In that sense, an extended domain was considered (mesh with ~250.000 cells), which increased the total domain by 100 mm around the whole reactor and in-cluded the 3 mm thick glass wall.

The present simulations consider an injection of 5 mL/min of fuel that is dispersed by 5 L/min of pure nitrogen (N₂). The initial size distribution of the droplets in the spray is represented by a Rosin-Rammler-Sperling-Bennet (RRSB) distribution. The pilot flame is composed of a mixture of methane (19% mass) and oxygen (81% mass).

The fuel is composed of pure p-xylene (C₈H₁₀) and its liquid and gaseous properties are taken from the works of Yaws [27], [28]. Two chemical reactions are present, the direct combustion of p-xylene and of methane which generates water (H₂O) and carbon dioxide (CO₂). The mathematical modeling and CFD approach used in this work are based on the works of Noriler et. al [29], [30], and Bianchi Neto et. al [26], [31], with one-step reaction mechanisms for combustion. The carbon black formation kinetics is explained in detail in the next section.

3. Carbon Black Kinetics

Here we adapt the mathematical modeling ap-proach proposed by Boulanger et. al [5], in which a three-equation model is solved to determine the mass fraction and size profiles of particles along the reactor. The model is based on the two-equation model devel-oped by Tesner et. al [6], where the authors' main con-tribution is to include a term for superficial growth of the soot particles, connecting fuel concentration and soot mass growth. The equations for Boulanger’s model are presented below:

(1)

(2)

(3)

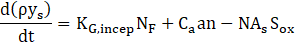
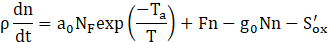
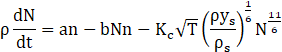
Where y_s is the soot mass fraction, n is the nuclei concentration, and N is number density of particles.  Furthermore, ρ is the fluid density, K_G,incep is the nucleation constant, N­_F is the concentration of fuel, C_a is the initial soot particle mass, A_s is the superficial particle area, S_ox and S´_ox are oxidation rates of particles and nuclei, respectively, which are described in detail by Boulanger et. al [5]. The constant a₀ is given as the vibration frequency of the bond to be broken, K_C is the coagulation coefficient, ρ_s is soot’s density, and a, g₀, F, and b are mathematical constants from the model. Also, T is the fluid temperature and T_a is the activation temperature for nuclei formation.

Eq. (1) refers to soot mass fraction (y_s) and its first term on the right-hand side refers to the superficial growth of particles. The second term on the right-hand side refers to the formation that arises from radical nuclei, and the last one is related to particle oxidation. Eq. (2) refers to the formation rate of radical nuclei (n), where the first term on the right-hand side represents the nuclei formation by fuel pyrolysis, and the second and third ones refer to the radical nuclei number growth through chain branching and destruction when landing on soot particles, respectively. Eq. (3) refers to the number density of soot particles (N), where the first and the second terms on the right-hand side are related to the numeric formation and termination of particles, respectively, and the last one refers to the coalescence process (as proposed by Fusco et. al [4]). The model has been implemented in ANSYS Fluent 19.2 through the use of user-defined functions (UDFs) as an adaptation of the already available two-step model (based on the work of Tesner et. al [6], [32]).

The influence of particle’s radiation in the process is taken into account by the model proposed by Sazhin [33], the gas absorption coefficient is calculated by Eq. (4),

(4)

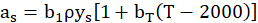
where a_s is the soot absorption coefficient, b₁ and b_T are model constants (b­₁ = 1232.4 m² kg^-1 and b­_T = 4.8e^-4 K^-1). ρ, y_s and T are local gas densities, carbon black mass fraction, and gas temperature, respectively. Results, where particle’s radiation is neglected, are shown in the next section.

4. Results and Discussion

In this section the different results obtained with the solution of the model are presented and discussed.

4. 1. Temperature

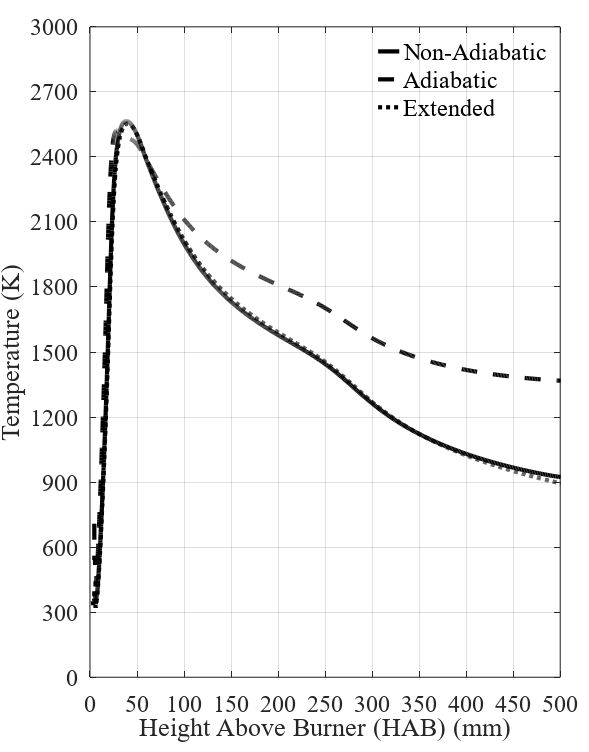
The results for temperature obtained in the simu-lations are presented in Figure 2. In the contour pre-sented on the left-hand side of the figure, a significant temperature difference is observed between the adia-batic and non-adiabatic cases, as expected. On the right-hand side, at the plot of temperature over the rector centerline, it is noticeable that the reactor, for the adia-batic case, is kept at high temperatures (higher than 1200 K) at the entire domain. The temperature peak for both cases is, however, very similar, at ~2500 K, which is because this region in the center is where most of the combustion occurs. The comparison between the results for the regular and extended meshes is also shown in the plot. As it is observed, the lines almost overlap showing that very similar results are obtained. These results show that the proposed value for the convective coefficient provides a satisfactory approximation, which is interesting given that the smaller mesh requires a lower computational cost for the solution.

4. 2. Carbon Black

Figure 3 and Figure 4 present the results concern-ing carbon black formation and evolution inside the re-actor for the adiabatic and non-adiabatic cases. The pre-sented profiles are values radially averaged along with the reactor height. The model proposed for the nanopar-ticles showed to be highly sensitive to temperature and composition profiles. The normalized concentration of radical nuclei, shown in Figure 3, is mostly affected by the oxidation rates, which are the greatest in the lower regions of the reactor where the combustion takes place. The number concentration of nanoparticles, also shown in Figure 3, presents a significant divergence between the studied cases.

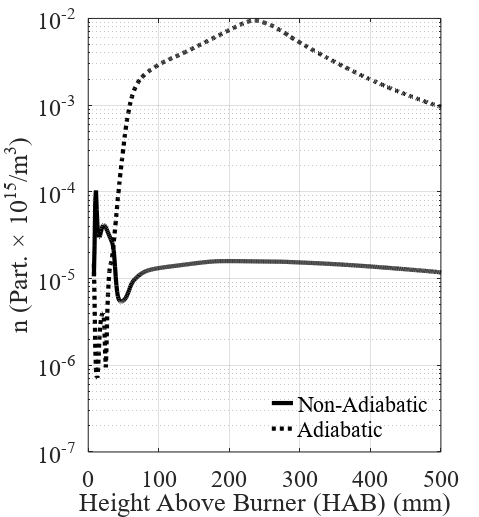
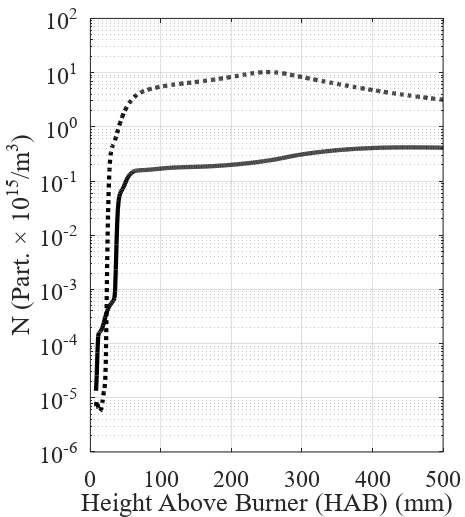
The higher temperatures observed in the adiabatic case increase the nucleation rates inside the domain, causing the concentration of nuclei to increase in the lower region of the reactor. The higher concentration of nuclei, in turn, increases the number concentration of carbon black.

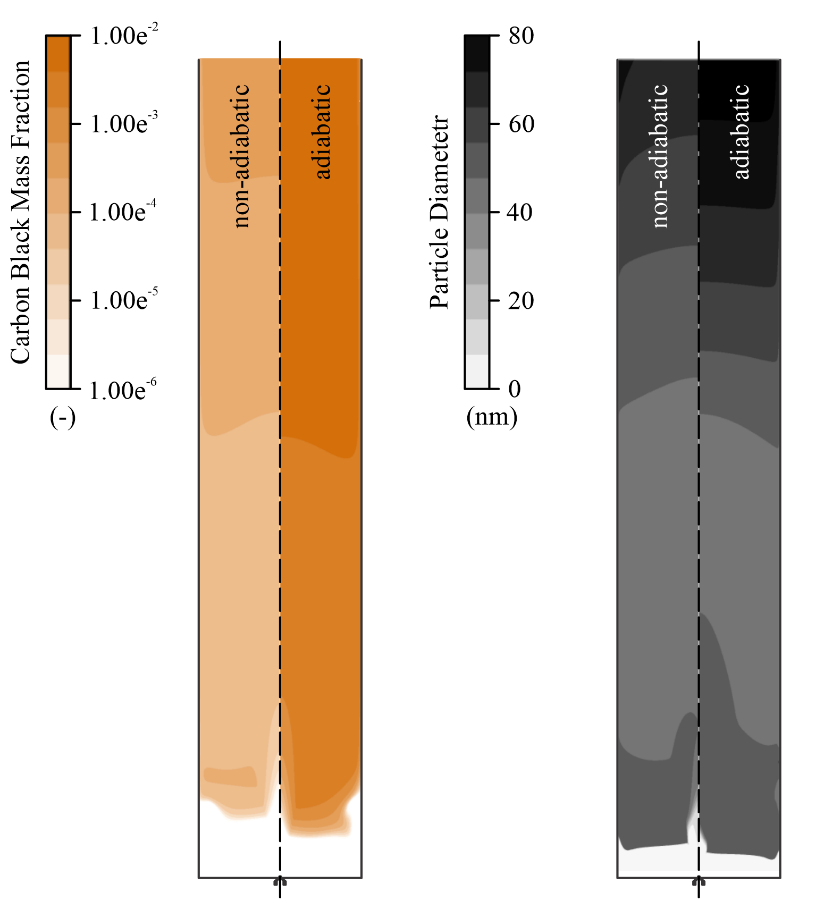
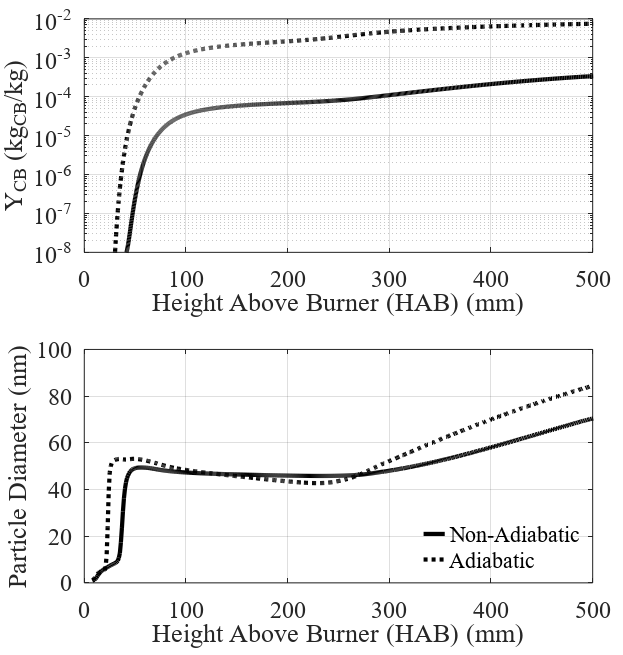
Contours of particle diameter and carbon black mass fraction are presented in Figure 4, accompanied by the profiles throughout the reactor. The mass fraction of carbon black follows the previous trend observed for the particle number concentration. As mentioned, the higher concentration of carbon black in the adiabatic case is due to the increased nucleation and chain branching rates due to the higher temperature. The results for par-ticle diameter show agreement with what is described in the literature [22]. In the hotter regions, the mean parti-cle size tends to decrease due to the high number of newly generated particles (peak of nuclei concentra-tion), at about 50 mm HAB. At 250 mm HAB, nuclei con-centration and inception of new particles decrease quickly, and the particle’s diameter returns to grow due to the surface growth term present in the model. Particle diameter continues to grow until the top-end of the reac-tor, indicating the continuation of the particle growth even after the particles leave the hotter regions of the reactor.

The observed results for both considered cases are very similar, which indicates that the temperature profile does not influence the final particle size signifi-cantly, even though a significant difference is observed in the total amount of soot produced.

4. 3. Influence of Particle Radiation

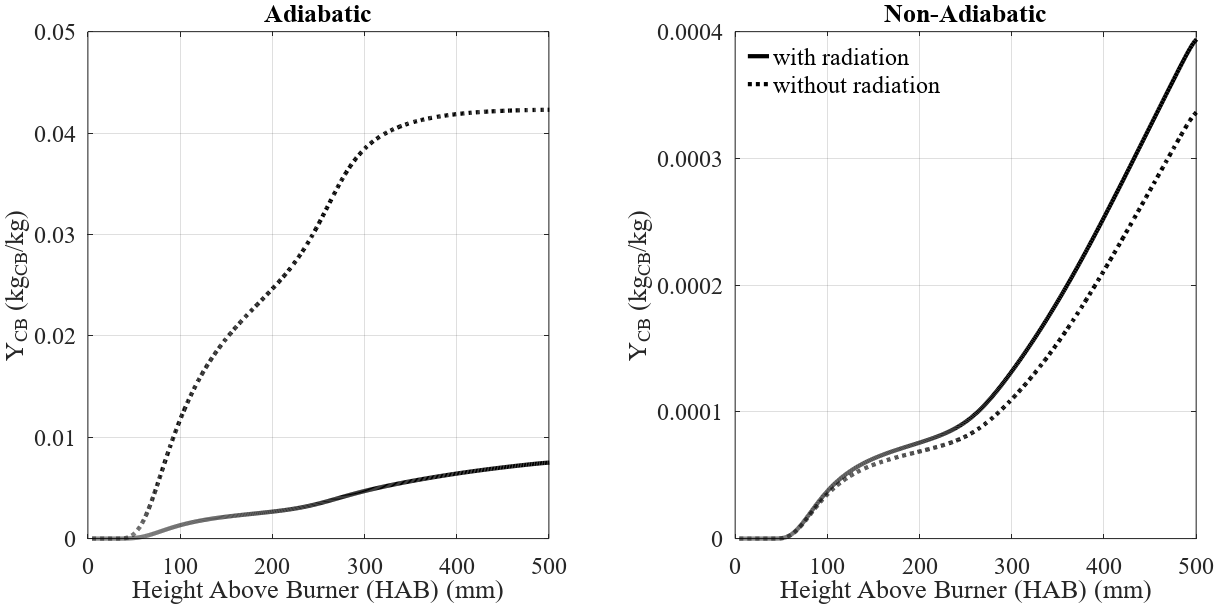
When studying the formation of soot and carbon black, the modeling of particle-radiation interaction, as described in Eq. (4), is important to avoid overestima-tions of flame temperature, which could affect the nano-particle formation kinetics. In Figure 5, results compar-ing cases with and without this phenomenon are pre-sented. For the adiabatic case, particle radiation has a very significant effect on the carbon black mass fraction produced inside the reactor. This is caused by an in-crease in the nucleation rate, generating more nuclei, which increases its chain branching process. The non-adiabatic case, on other hand, presents very low varia-tion between the profiles, due to the relatively small carbon black production in this case. A significant tem-perature profile is observed only for the adiabatic case, due to high quantities of carbon black mass fraction, which affects the radiation model employed (Eq. (4)).

5. Conclusion

In this work, CFD simulations of the production of carbon black via the FSP process were carried out, cou-pled with a monodisperse PBM. Initial results showed that the use of an average value for the convective coef-ficient at the reactor walls is appropriate, avoiding the need for the discretization of the air surrounding the reactor. This simplification reduces the final size of the numerical mesh, cheapening the necessary computa-tional cost.

Additional results indicated that with the use of thermal insulation in the reactor walls, a much higher temperature profile is observed. The effects of this hot-ter domain on the final particle diameter are not very significant, the final quantity of the material, however, is greater, given that the temperature directly influences the nucleation and oxidation rates of the carbon black. In that sense, the practice of insulating the reactor has the potential for process design allowing for a more con-trolled quenching of the system.

Finally, the influence of particle radiation on the fi-nal product was meant only for the adiabatic case, given the high concentrations of the nanomaterial in the reac-tor. This phenomenon, however, should be further in-vestigated and experimental data should be used for model validation.

Acknowledgments

This study received funding from the São Paulo Research Foundation – FAPESP (Project ID: 2020/08502-9 and 2021/01067-8), in Brazil. Additional acknowledgment is also directed to the Coordination of Higher Educational Personnel – CAPES (Process ID: BEX 12369/12-8).

References