Journal of Fluid Flow, Heat and Mass Transfer (JFFHMT)

ISSN: 2368-6111

1. Introduction

Thermoacoustics combines thermodynamics, fluid dynamics and acoustics to describe the interaction between heat and sound. Under the right operating conditions thermoacoustic concepts can be applied to realize two kinds of devices: thermoacoustic refrigerator or heat pump that convert sound wave energy in refrigeration or heating, thermoacoustic engine that convert heat in useful work [1]. Thermoacoustic technology can play a significant role in the development of renewable energies because of its advantages over conventional energetic technologies: environmentally friendly working fluid (air, noble gases), low-grade energy inputs (industrial waste heat, solar energy) can be used as driving sources, no moving part (high reliability), low manufacturing and maintenance costs [2]. Energy conversion takes place in a particular porous material which represents the core of these devices. It is named “stack” or “regenerator” depending on the typology of the device, respectively for standing wave or traveling wave. Stacks need to be suitably dimensioned on the thermal and viscous penetration depth to allow the energy conversion minimizing the viscous losses and ensuring the correct thermal interaction between fluid and solid skeleton. In literature, classical uniform cross-section geometries, such as parallel plates, circular, squared and hexagonal pores, usually employed as stack, are described from a thermoacoustic point of view by an analytical formulation [3]. Swift [4] highlighted the properties of convex geometries, such as pin array, which have greater efficiency than the concave ones in the thermoacoustic energy conversion. Additionally, stacks must have a low thermal conductivity in order to be able to sustain the thermal gradient along it. Matveev [5] underlined the possibility to use stacks made by transversal pin array to reduce the thermal conductivity. Based on these assumptions, Auriemma et al. [6] highlighted the possibility to employ tetragonal pin array as thermoacoustic stack to find a trade-off between the classical longitudinal pin array (uniform cross-section, low viscous losses and high thermal conductivity) and the transversal pin array (high viscous losses and low thermal conductivity). Dragonetti et al. [7] pointed out the relationship between the acoustic and thermoacoustic descriptions, which allows to use the classical acoustic semi-phenomenological model to describe the thermoacoustic performance of porous material with complex microgeometry, such as fibers, foams and granular materials. In Di Giulio et al. [8], geometrical correlations for transport parameters are provided in order to have a dynamic thermo-viscous description for the thermoacoustic behaviour of the tetragonal pin array stack. The aim of the present work is to obtain an efficient geometrical model to assess the effective thermal conductivity of tetragonal pin array stack. Once the thermal conductivity model is known, the complete acoustic and thermal characterization of the tetragonal pin array allows to estimate correctly the performance of such materials in thermoacoustic engine and heat pump.

2. Thermoacoustic Background

Thermoacoustic phenomena inside a porous core, generally referred as “stack” in standing wave device, can be analytically described through linearized Navies-Stokes equation, coupled with continuity equation in frequency domain (said ω=2πf the angular frequency):

1

2

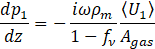
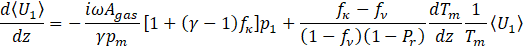
where p where p₁ and 〈U₁ 〉 indicates the acoustic pressure and the mean value of volume velocity on the cross section of material. ρ_m, p_m, T_m are respectively the static density, pressure and temperature and γ, P_r are the specific heat ratio and the Prandtl number of the fluid, i=√(-1). A_gas is related to the cross-sectional area of the material A through the porosity A_gas=Aφ. Viscous and thermal dynamic properties of the stack are described by the terms f_ν and f_κ, which are called Rott’s functions. They are complex and frequency-dependent parameters depending on the microstructure of porous stack and on viscous and thermal penetration depth

3

μ,k_f,c_p are the viscosity, the thermal conductivity, and the heat capacity at constant pressure. To completely solve the acoustic fields p_1, (z), 〈U₁ (z)〉 and the temperature distribution T_m (z) along the stack, a third equation is needed, and it is found to be the total power H equation

4

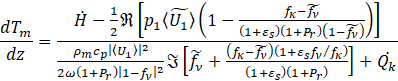
The symbol ~ denotes the complex conjugate, R and I indicate the real and imaginary part of complex number. ε_s is a correction factor for finite solid heat capacity [9]. represents the conductive heat power along the stack due to the thermal gradient. Swift [1] evaluated as

5

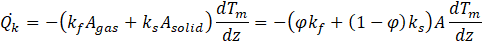
where k_s is the thermal conductivity of the solid skeleton of the porous stack. Eq. (5) can be considered valid for uniform cross-sectional material, such as parallel plates, circular pores and longitudinal pin arrays, where heat flows in parallel between fluid and solid. For porous materials with a random solid skeleton distribution a more generic formulation of Eq. (5) is

6

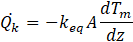
k_eq is the equivalent thermal conductivity of the porous medium and it depends both on fluid and solid thermal conductivity, the porosity and a geometrical factor which represents the solid distribution over the fluid in the porous material.

2. 1. Tetragonal Pin Array

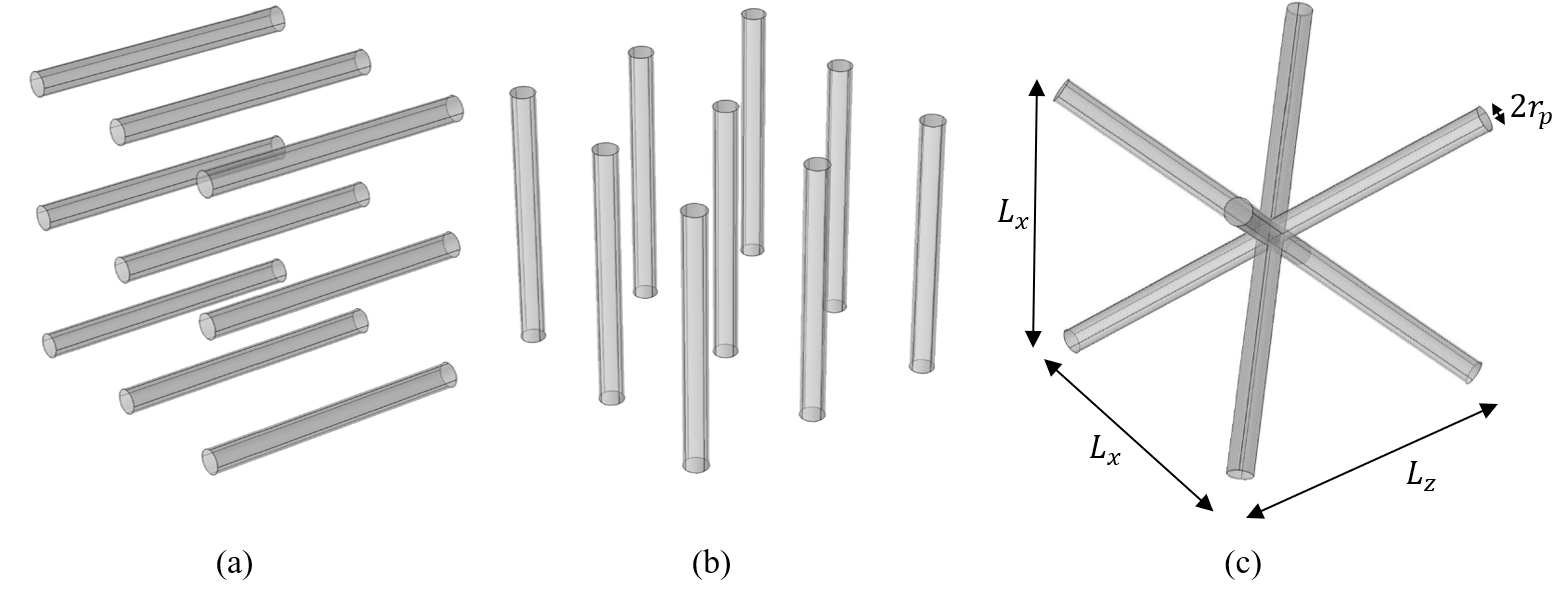
In [4], Swift pointed out the fact that convex geometries, such as pin array, have better performance than concave ones in thermoacoustic energy conversion, see Fig. 1a. The reason is due to the higher ratio between the thermal and viscous diffusion areas in convex geometries. In fact, moment and thermal diffusion occur in a region of fluid on thickness δ_ν and δ_κ. As a consequence, for convex geometries, the total volume involved in thermal diffusion in sensibly larger than that involved in viscous losses. Matveev [5] and Petlucescu [10] underlined the possibility to employ transversal pin array respect to the wave propagation (Fig. 1b.). In fact, dynamic thermal function f_κ depends on the scalar field of temperature and it does not change with the pin orientation. Additionally, transversal pins are not uniform cross-sectional and realize a much lower thermal conductivity k_eq than the longitudinal ones which allows to sustain the thermal gradient. From the viscous point of view, dynamic viscous function f_ν is expressed as function of vectorial field of velocity and it is sensible to pin orientation. In particular, viscous losses are higher in transversal pins due to the increasing tortuosity respect to the classical horizontal pins.

From these two aspects, the compromise between low viscous losses and low thermal conductivity is reached in the tetragonal pin array, reported in Fig. 1c.

Dragonetti et al. [7] pointed out the link between thermo-viscous functions and complex density and bulk modulus, usually used in sound absorption for the equivalent fluid description of porous media. Thanks to this bridge between acoustic and thermoacoustic characterization of materials, the Johnson-Champoux-Allard-Lafarge [11–13] semi-phenomenological model (JCAL) can be used to describe the behaviour of a generic porous media employed as stack in a thermoacoustic device. The input of JCAL model are six transport parameters: the porosity φ, the thermal and viscous characteristic lengths Λ^' and Λ, the static thermal and viscous permeability k₀^' and k₀, the high frequency limit of tortuosity α_∞. In Di Giulio et al. [8] correlations for the transport parameters for tetragonal pin array with square base are provided as function of dimensionless size of the unit cell , where r_p is the pin radius.

7

where A_i=1..6 are numerical constant of the model. Based on these geometrical correlations, the JCAL model and the Dragonetti et al. relations, dynamic thermo-viscous behaviour of the tetragonal pin array can be expressed in terms of its Rott’s function f_ν and f_κ.

To complete the description of the tetragonal pin array structures, an analytical formulation of the equivalent thermal conductivity k_eq is needed to correctly assess the heat power .

3. Thermal Conductivity Model

In literature, several models have been provided to predict the thermal conductivity of two-phase composites [14]. Pin array can be mainly associated to fibrous materials, for which thermal conductivity model have been developed by [15–18]. Generally, fibers networks are composed by a large number of struts statistically oriented in the space, while pin array stack is characterized by a precise controlled geometry. Therefore, the aim is to have a thermal conductivity model particularized for the tetragonal with square base pin array depending on the pins ‘orientation. The two-limit cases for the thermal conductivity are represented by the longitudinal k_L and the transversal k_T pin array, which analytical description are available

8

9

An analytical model for thermal conductivity of tetragonal pin array is developed as weighted average between k_L and k_T,

10

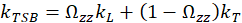
The subscript TSB means Tetragonal with Square Base and is the geometrical parameter indicating the orientation of the pin array to respect the thermal gradient direction.

Since the parallel and transversal formulations of conductivity depend on the porosity φ, assessed through Di Giulio et al. [8] correlation, the proposed relation for the thermal conductivity k_TSB is function only of the geometrical parameters of the unit cell (L_x,L_z,r_p ).

3. 1. Numerical simulations

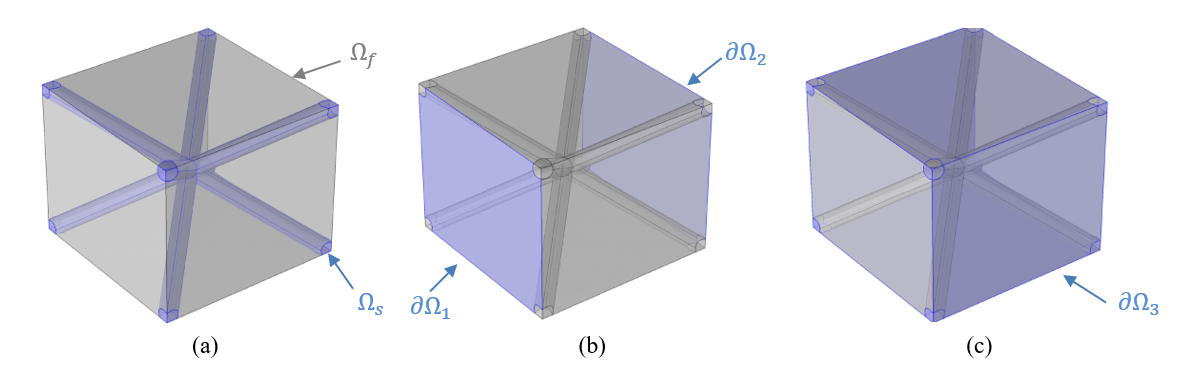
Finite Element simulations have been carried out on the Representative Elementary Volume of the Tetragonal pin array porous material to verify the previous analytical expression of the effective thermal conductivity k_eq In Fig. 2.a., the fluid and solid volume fractions, respectively Ω_f and Ω_s, in which the thermal problem is solved, are shown. A temperature gradient is applied on the unit cell (T=T₁ on ∂Ω₂ and T=T₂ on ∂Ω₂, first type Dirichlet’s boundary conditions in Fig. 2.b.), while symmetry boundary conditions are imposed on the lateral boundaries (∇T ⋅n=0, Fig. 2.c.) to reproduce the periodicity of the elementary volume. Based on these assumptions, the effective thermal conductivity can be assessed by picking up the volume average heat flux value along the thermal gradient ∇T direction

11

4. Results and Discussion

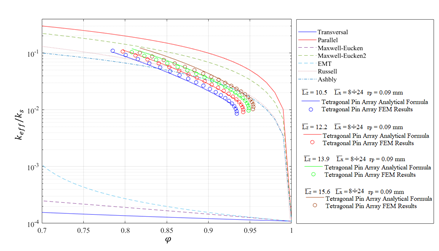
Simulations have been conducted on 200 different Tetragonal pin array unit cells obtained by varying the dimensionless geometrical parameters  and in a range between 8 and 24. Literature’s models, the provided relation for k_TBS, Eq. (10), and FEM data are compared in Fig. 3. Results are shown in terms of the dimensionless effective thermal conductivity k_eff/k_s as function of the porosity φ For legibility of the plot in Fig. 3, numerical results are reported by fixing four values and varying As it can be seen, literature’s models are not depending on the orientation on the pin array, while a good agreement between the proposed formula and FEM results is found.

The heat and mass transfer coefficients in the drum were calculated by applying these formulas used in the literature.

The following assumptions were made in the modeling studies.

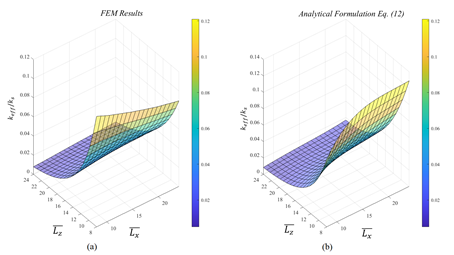
Surface plots in Fig. 4.a. and 4.b. show the agreement all over the chosen range of dimensionless parameters and between the numerical results and the provided analytical formulation. As it can be seen, the effective thermal conductivity increases for low value of given how porosity strongly decreases and then solid fraction increases. On the other hand, when the unit cell size rises, the percentual amount of solid inclusion drops and k_TBS tends to k_f.

5. Conclusion

An analytical formulation to assess the effective thermal conductivity of tetragonal with square base pin array has been provided. It has been expressed as function of geometrical dimensionless parameters representing the period unit cell. Numerical simulations support the proposed formulation in the evaluation of the heat flux along this typology of porous material once they are subjected to a thermal gradient. Coupled with the correlation in [8], the provided model completes the characterization of the acoustic and thermal behaviour this porous material. Furter studies will carried out to assess the performance of thermoacoustic engine and heat pump employing this porous core as stack.

Acknowledgements

This work was partly supported by Italian Ministry of University and Research (MIUR): Project number PRIN 2017JP8PHK.

References