Volume 8 - Year 2021 - Pages 178-188
DOI: 10.11159/jffhmt.2021.020
Quenching Hot Rotary Hollow Cylinder by 1-row and 2-row Water Impinging Jet Array
Mohammad Jahedi1, Bahram Moshfegh1,2
1Department of Building Engineering, Energy Systems and Sustainability Science, University of Gävle
801 76, Gävle, Sweden
Mohammad.jahedi@hig.se; bahram.moshfegh@hig.se
2Department of Management and Engineering, Linköping University
583 30, Linköping, Sweden
Abstract - Experimental study has been carried out to investigate transient quenching of rotary hollow cylinder by subcooled water impinging jets (∆Tsub= 55-85K) in 1-row and 2-row inline array. The flow rate of water jets varied from 2.7 to 10.9 L/min, impinging on hot rotary cylinder (Ti =600℃) with rotation speed 10-50 rpm and different curvature ratio (Do/d = 12, 19 and 24). The local average and maximum boiling heat transfer at water jet’s stagnation point revealed effect of studied quenching parameters and multiple jet arrays in the boiling heat transfer. The result showed among the studied parameters, jet’s flow rate and curvature ratio influenced heat transfer in all the boiling regimes. Rotation speed was effective in film and transition boiling regime and strong effect of subcooling was captured in the transition boiling regime. The characteristics of maximum heat flux point in the boiling curve were found to be dependent on the studied quenching parameters as well as array of nozzles. Multiple jet arrays had effect on the spatial variation and rate of boiling heat transfer on quenching surface. The heat transfer enhancement by larger number of rows, i.e. 2-row array, was studied based on two approaches of constant single jet’s flow rate and array’s total flow rate. The result shown better heat transfer performance is achieved by increasing number of row in the array while the total flow rate is constant. It was found that by impinging constant water flow rate into the jets, 2-row array with twice the number of impinging jets enhanced heat transfer significantly in film and transition boiling regime in combination with other quenching parameters.
Keywords: Multiple jet arrays, Transient boiling, Rotating surface, unsteady inverse heat conduction problem, Quenching, Water impinging jet.
© Copyright 2021 Authors - This is an Open Access article published under the Creative Commons Attribution License terms Creative Commons Attribution License terms. Unrestricted use, distribution, and reproduction in any medium are permitted, provided the original work is properly cited.
Date Received: 2021-01-13
Date Accepted: 2021-01-15
Date Published: 2021-03-10
1. Introduction
More advanced controllable quenching techniques are of interest in the metal industry to optimize the efficiency of cooling processes resulting in improved material properties and quality. Among the cooling methods that are used, quenching hot metal surfaces by water impinging jet is one of the best-known and effective methods. In solid-liquid contact over the quenching surface, boiling phenomena occur and introduce various boiling regimes during the cooling process.
In the water impinging technique, the water jet’s flow is impinged toward the hot surface and experiences constraint by the surface resulting in changing flow direction into a wall-jet shape. In the first moments, water flow is deflected to surroundings due to very large temperature difference between solid and liquid. The surface temperature around the stagnation point of impingement drops very fast and a circular wetted zone is formed over the surface. By passing the resident time [1], the wetted zone surrounding the stagnation region of water jet starts to grow while its edge experiences nucleate and transition boiling condition [2]. Further in radial distance from stagnation point, annular transition zone (also known as wetting front region [3]) exists where water flow is splashed away as water drops are in contact with the hot dry zone [4].
In the study of boiling heat transfer and its characteristics on quenching a flat surface by single water impinging jet, various parameters need to be considered. Some of the reported important parameters are liquid subcooling [5], impinging jet diameter [6, 7], single water jet flow rate [5, 8], material properties of quenching surface [9], initial temperature of quenching [10] and jet-to-surface spacing [5, 8]. In real conditions in the metal industry, quenching is often applied on moving hot metal product on the run-out table which introduces surface moving speed as an additional parameter [11]. This causes the wetted and wetting front (WF) region to become asymmetric by hydraulic jump in one side of wetting front region [12]. In practice, in order to apply the water jet quenching technique, several water jets are needed to be placed in multiple array to cover large hot surfaces. Vakili and Gadala [13] performed quenching experiment on a moving hot flat surface by in-line and staggered arrays of nozzles and showed that lowest spatial variation of cooling occurred with staggered arrays of jets. They also reported lower surface heat flux by increasing surface moving speed in high entry temperature.
Despite the good literature on the quenching of hot flat surfaces, few research studies performed quenching on a cylinder surface by single water jet. Quenching such geometry represents boiling phenomena over a convex surface. In practice, rotation exists on run-out table which introduces new features in the hydrodynamic of boiling. The surface experiences cooling under the wetted and wetting front regions and then enters a dry zone where temperature recovery occurs due to internal conduction heat transfer inside material until the surface approaches the wetted and wetting front region in the next revolution cycle. This characteristic leads to cyclic fluctuation of heat flux depending on rotation speed of cylinder and its footprint is found in the boiling curve [14, 15]. The similarity between growth of wetted region and wetting front over rotary cylinder and moving flat surface is the hydraulic jump on one side and stretched wetted and wetting front regions in the moving direction [16, 17].
Similar to quenching of large flat surface, multiple jet array is required for quenching of large and long tubes and bars in practice. There are only a few studies that have investigated hydrodynamics of boiling phenomena and heat transfer characteristics affected by the quenching parameters. Jahedi and Moshfegh [18] studied quenching of a rotary cylinder by 1-row array of subcooled water jets and reported temperature and cooling rate variation near the surface influenced by water jet flow rate, subcooling, impingement impact angle, rotation speed, initial quenching temperature and jet-to-jet spacing, which is the new parameter in the quenching technique. Smaller spacing between jets (S/d ≤ 4) provides more uniform cooling rate over the quenching surface. But larger spacing creates better interaction between neighbor jets, and results in high cooling rate region in this zone.
In the interaction zone, WF of neighboring jets collide with each other thus forming upward fountain flow, a mechanism to discharge WF from the surface. In a recent study, Jahedi and Moshfegh [19] investigated hydrodynamic phenomena of interactions between water jets over rotary cylinder quenched by 1-row and 2-row in-line multiple jet arrays and presented two types of interactions between jets; lateral upwash flow is formed by WF interaction of neighbor jets in 1-row array and secondary interaction occurs in 2-row configuration of nozzles between WF of jets in adjacent rows which is called longitudinal upwash flow. They reported the discharged mechanism behavior led to high surface heat flux in the lateral upwash flow zone, which is in agreement with the previous studies on flat surface quenching [13, 20]. They also studied quenching parameters’ influence on average heat transfer over quenching surface, local heat transfer at stagnation point of water jet and lateral upwash flow point in the 1-row multiple jet array.
From the above-mentioned literature, only a few studies have been carried out on quenching of convex surfaces by multiple pitch of water jets (1-row pitch). Therefore for this study, authors intended to present the experimental results on 1-row and 2-row in-line arrays of water jets on the quenching of rotary cylinder (convex surface) to provide better understanding of the effect of multiple arrays together with quenching parameters on the local boiling heat transfer.
2. Experimental Procedure
2.1. Experimental Setup
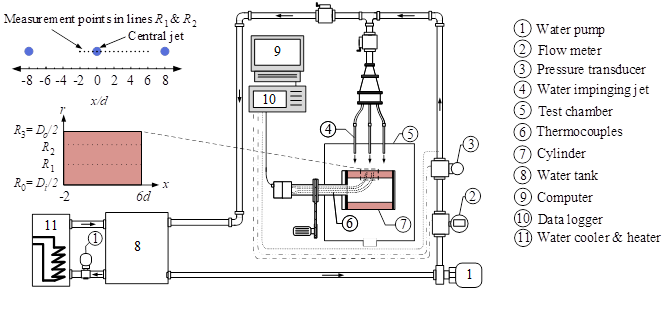
Fig. 1 presents a schematic of the experimental setup and nozzle configuration with respect to temperature measurement points. 1-row and 2-row in-line multiple jet arrays of subcooled water impinging jets were used to quench a hollow cylinder. Test specimen was rotated during the quenching experiment to mimic actual condition of run-out table in industry.
Temperature data was acquired by grounded N-type thermocouple with 0.75 mm probe diameter mounted in two different depths (R1 and R2) in the hollow cylinder near the quenching surface (R3). DAQ system connected to LabVIEW program monitored and recorded temperature and water flow rate signals during the experiment. Water temperature in the tank was regulated by water cooler and heater in an internal circulation. Regulation and measurement of water flow rate in the piping system was done by water pump and magnetic flow meter respectively. Rotation speed of hollow cylinder was adjusted by controller of servo motor. When initial quenching temperature reached slightly above 600°C in the heating process by induction heater, the LabVIEW program was able to send pulse signal to solenoid valves to switch water flow from internal circulation toward multiple arrays of impinging jets. Full description of experimental process of the quenching has been reported by Jahedi and Moshfegh [18].
In this study, effect of various parameters of quenching was investigated on cooling of the rotary hollow cylinder impinged by 1-row and 2-row array of multiple water impinging jets. Table 1 shows designed range of the parameters investigated in this study.
Table 1: Designed parameters in the experimental study.
| Parameter | Range | Unit |
| Q | 2.7, 5.4, 10.9 | L/min |
| ∆Tsub | 55, 75, 85 | K |
| Do/d | 12, 19, 24 | - |
| ω | 10, 30, 50 | rpm |
| N | 1, 2 | - |
| array | In-line | - |
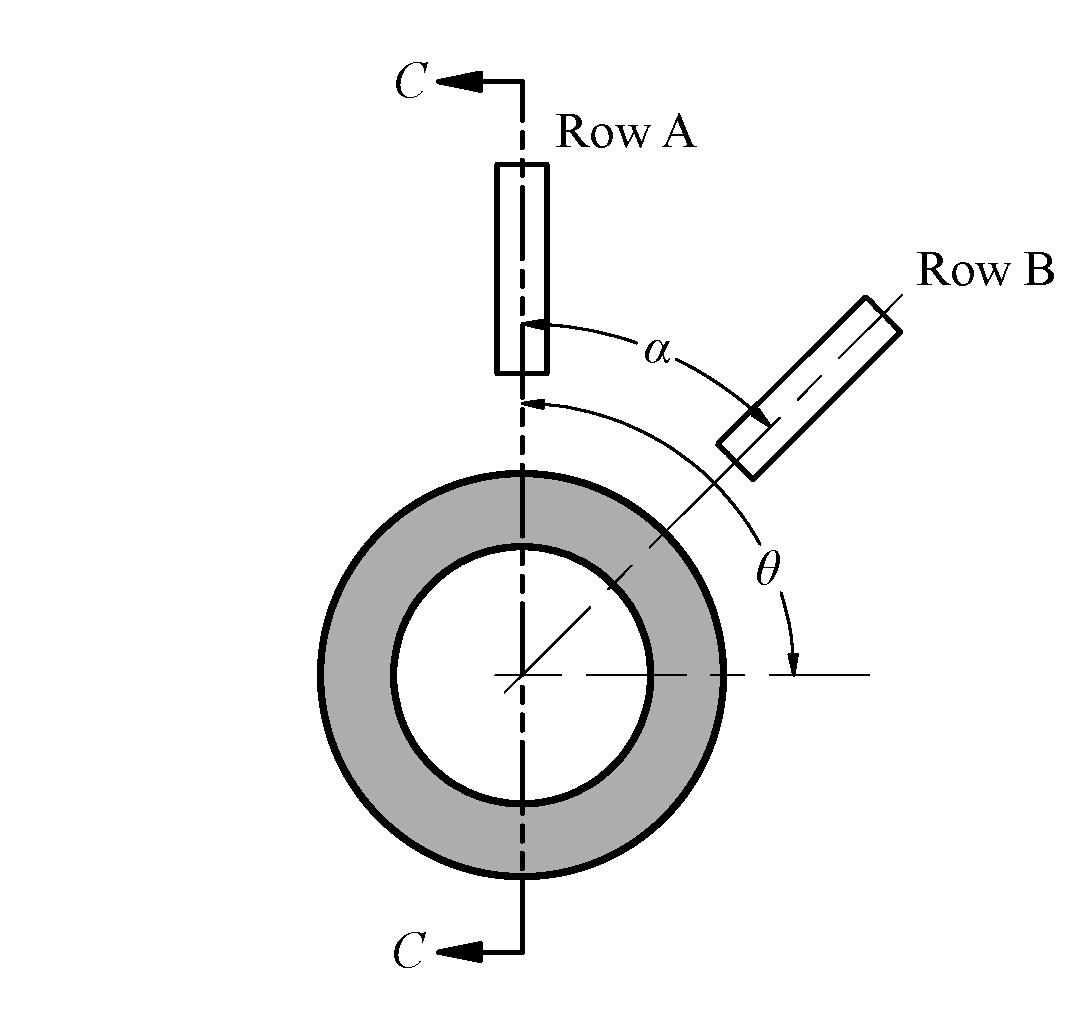
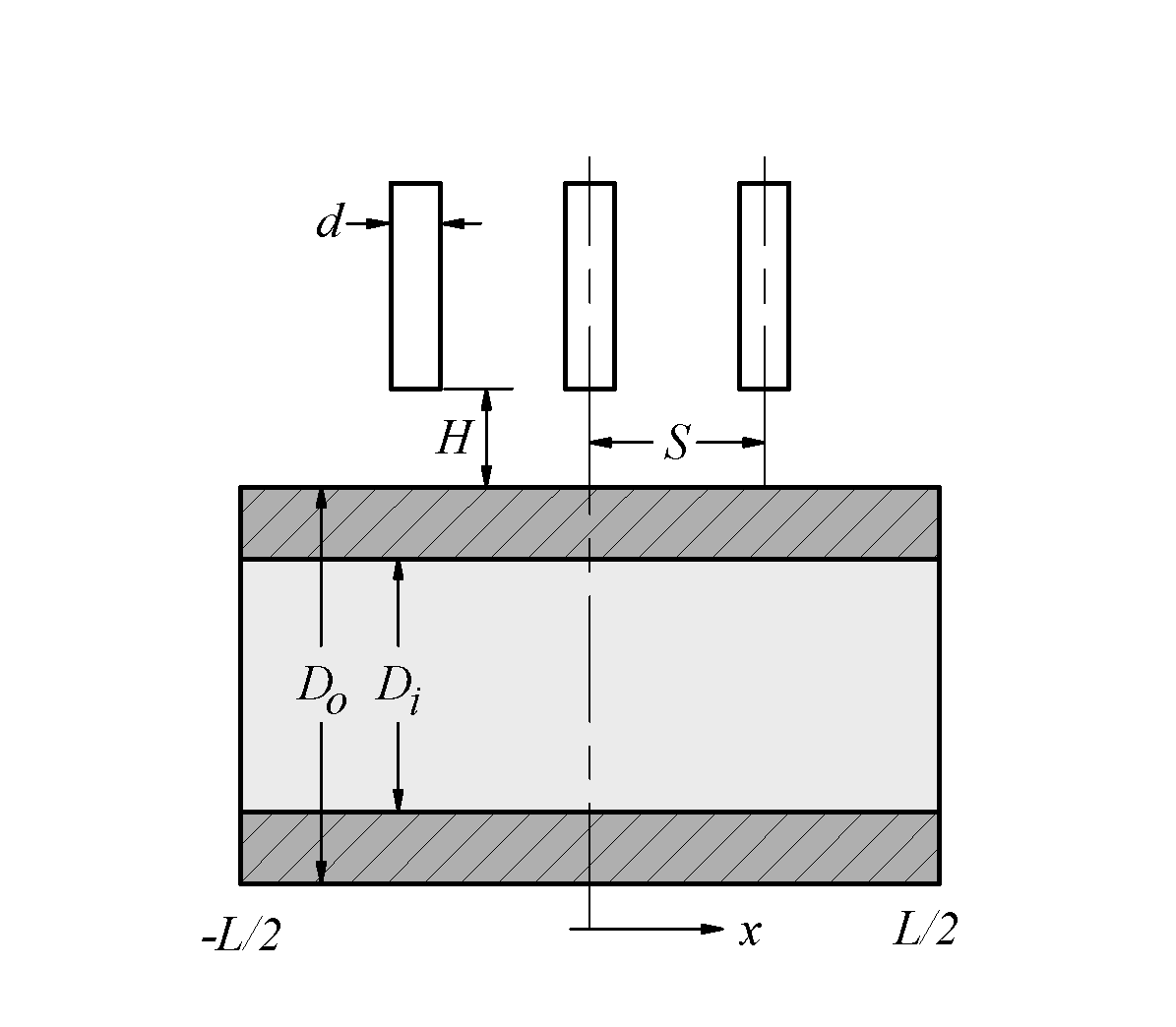
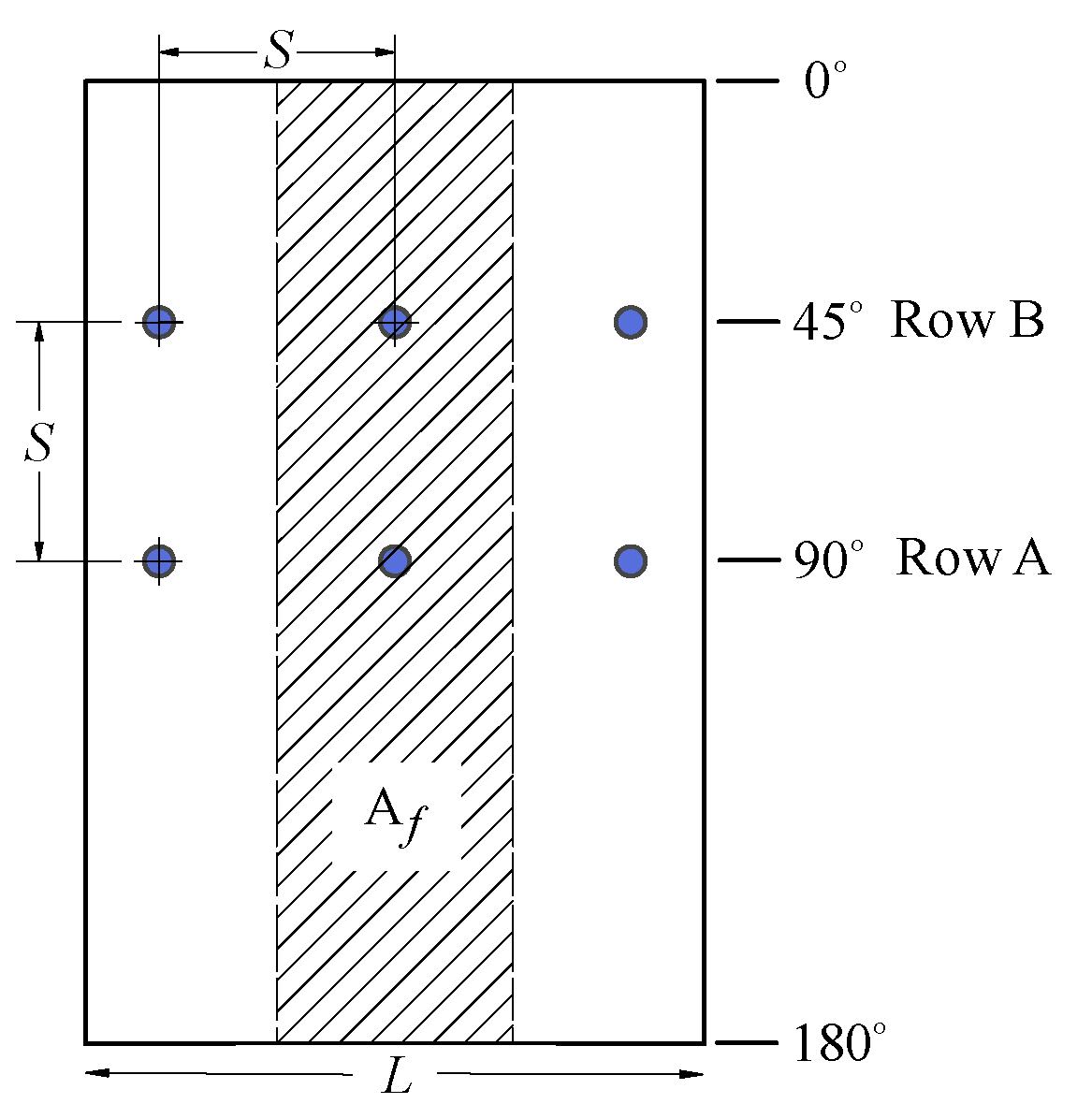
The round jet diameter (d) was 8 mm with jet-to-wall spacing H/d = 1.5, jet-to-jet spacing S/d = 6 and the angles α and θ in the configuration were 45 and 90° , respectively. The hollow cylinder’s outer diameter (Do) was 96, 152 and 192 mm with the outer to inner diameter ratio Do ⁄Di= 1.56, 1.59 and 1.54 respectively and length L =173 mm, see Fig. 1. N stands for number of rows an appellation Row A was used in the 1-row pitch and Row A and B were applied in the 2-row in-line array. The maximum uncertainty of calibrated thermocouple sensor and data acquisition system was ±1.1% at a temperature of 100°C. The uncertainty of thermocouple sensor location, water flow rate and water temperature were ±4.6, ±1.4 and ±4.7%, respectively.
2.2. Data Reduction
In order to understand hydrodynamic phenomena of boiling and effect of the parameters on quenching heat transfer, studying the surface heat flux and temperature is of interest since boiling occurs on quenching surface when liquid and solid interact with each other. Surface temperature measurement is challenging as temperature sensors may disturb water flow field on the surface or cannot withstand harsh conditions during the heating and cooling process. One way to overcome this problem is to apply an inverse solution technique to determine the surface temperature and heat flux. In this study, the generalized minimal residual method (GMRES) [21] developed by Jahedi, et al. [15] for application of quenching rotary hollow cylinder by water impinging jets was used. In this inverse problem technique, recorded interior temperature data of cylinder at two different depths from quenching surface (line R1 and R2) is applied as input into the GMRES method to predict surface temperature and heat flux at line R3, see Fig. 1.
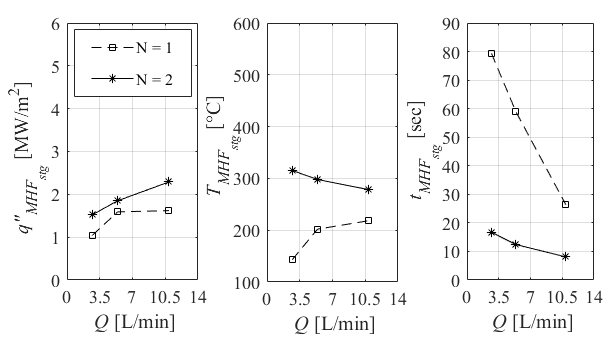
In order to calculate average heat transfer in the boiling regimes, Leidenfrost temperature was calculated based on reported value by Jahedi and Moshfegh [19]. Local maximum heat flux (MHF) and corresponding temperature (TMHF) are obtained from boiling curve (Fig. 3) and time to reach this point (tMHF) is extracted from the heat flux graph. Since MHF is shifted from nucleate boiling toward higher temperature level by some parameters, the corresponding temperature to CHF in onset of nucleate regime is picked up from the boiling curve of experiments where no higher heat flux is captured in lower temperatures in the nucleate regime.
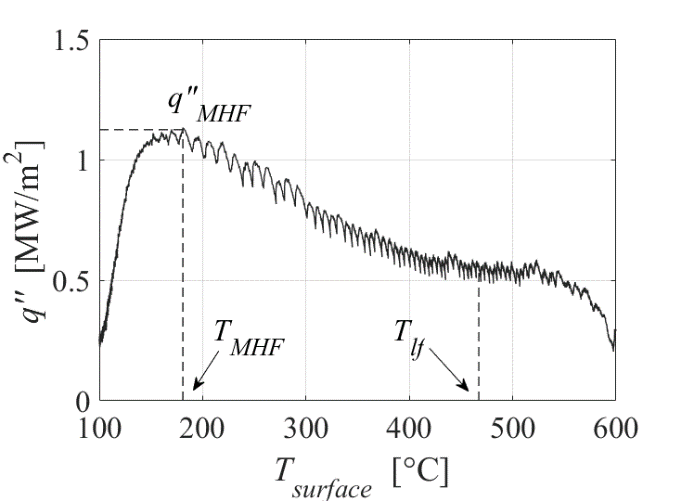
The jet flow rate is a key parameter in the impinging jet technique, which can be implemented as Uj into the surface heat flux to convert it to a dimensionless parameter (![]() ). This dimensionless parameter relates impingement heat transfer performance to the impinging flow rate in the array and multiple array configuration.
). This dimensionless parameter relates impingement heat transfer performance to the impinging flow rate in the array and multiple array configuration.
In the impingement of water into the multiple array, the relation between the total flow rate (Qtotal) in the array and jet’s flow rate becomes
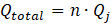
Where n is number of jets in the array and
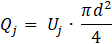
The relation in Eq. (2.1) can be evaluated within two approaches in term of impingement cooling of multiple arrays. The first approach focuses on the individual jet’s flow rate in the array (Qj) by keeping it constant in various multiple arrays. As a result Qtotal becomes double as number of jets in the 2-row array are twice compare to 1-row array. However, in the second approach, Qtotal, is kept constant in the arrays, which leads to decrease of Qj in each individual jet in the 2-row compare to 1-row array.
3. Results and Discussion
3.1. Multiple Array of Jets
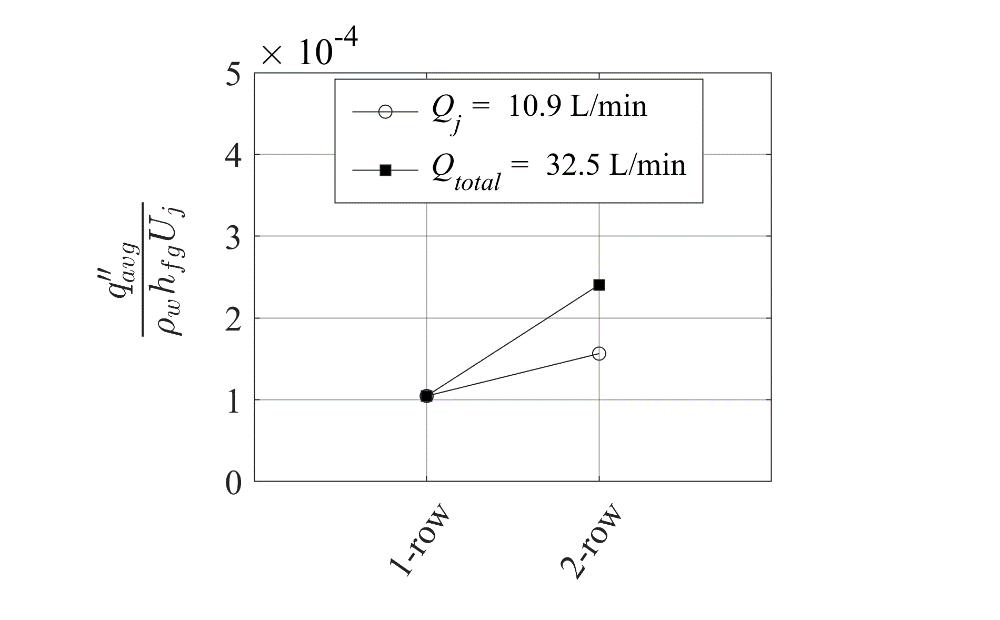
In the study of boiling heat transfer by multiple water impinging jets, it is important to evaluate the heat transfer performance of multiple array (![]() ) by two approaches which are described in the Section (2.2). Fig. 4 presents only small increase of heat transfer performance over the cooling area, Af, in the first approach (Qj=constant) with twice of number of row in the array (twice Qtotal). However, the result of second approach (Qtotal=constant) shows the combination of extended wetted region by larger N and smaller Qj enhances the heat transfer performance significantly. This result shows that enhancement of average boiling heat transfer in the multiple array configuration is not proportional with increase of total flow rate in the array and therefore it does not always lead to increment of the heat transfer performance by multiple array.
) by two approaches which are described in the Section (2.2). Fig. 4 presents only small increase of heat transfer performance over the cooling area, Af, in the first approach (Qj=constant) with twice of number of row in the array (twice Qtotal). However, the result of second approach (Qtotal=constant) shows the combination of extended wetted region by larger N and smaller Qj enhances the heat transfer performance significantly. This result shows that enhancement of average boiling heat transfer in the multiple array configuration is not proportional with increase of total flow rate in the array and therefore it does not always lead to increment of the heat transfer performance by multiple array.
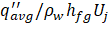 ) in experiments with Ti=600℃, ω= 50 rpm, ∆Tsub= 75 K and Do/d = 24.
) in experiments with Ti=600℃, ω= 50 rpm, ∆Tsub= 75 K and Do/d = 24.
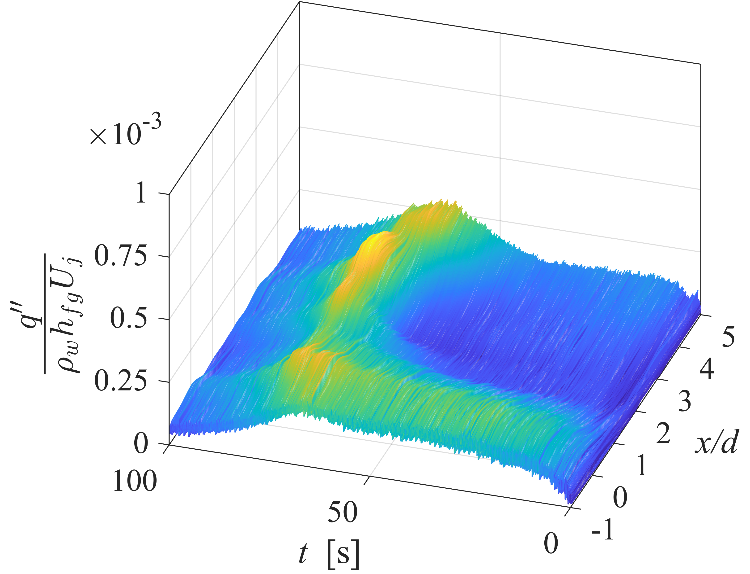
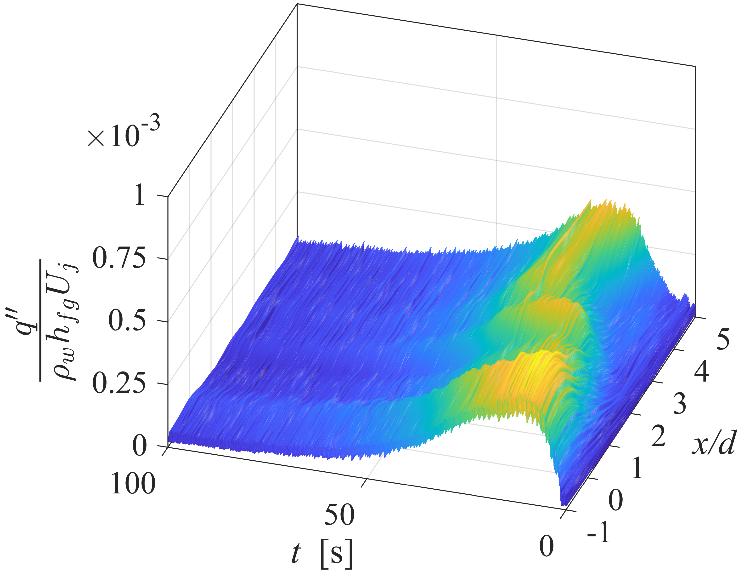
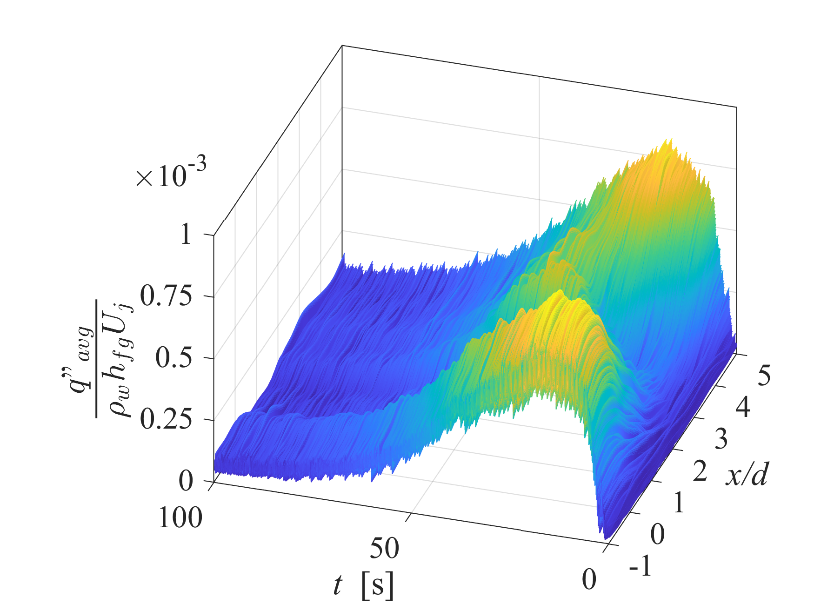
In more detailed analysis, local cooling rate variation in time is important as it can be compared with desired cooling curve in the CCT diagram of quenching. In this manner, Fig. 5 presents surface heat transfer performance of various quenching experiments with 1-row and 2-row array for the studied two approaches. The MHF is achieved with large time delay at the stagnation point (x/d = 0) and upwash flow point (x/d = 3) in the 1-row array in Fig. 5a. In the 2-row array, the poor cooling area in onset of boiling is suppressed in experiments within approach one (Fig. 5b) and is almost vanished within approach two (Fig. 5c). This result show the importance of the multiple array configuration and coverage of boiling surface with more nozzles in the array. The heat transfer performance (![]() ) enhances to the peak value and drops significantly in a shorter time with 2-row array compare to 1-row array in both approaches, which is a proof of improvement of cooling in term of quenching time duration with 2-row multiple array. In the 2-row array, higher heat transfer performance is obtained in the second approach where Uj decreases 50% while the quenching area is extended. In the study of various Do/d in hollow cylinder, author captured very similar trend of heat transfer variation over Af with 1-row and 2-row arrays. However, the time delay to onset of surface heat flux enhancement was reduced gradually and higher heat flux rate was achieved with smaller Do/d. It may be concluded that there is a tradeoff between the multiple array configuration and the flow rate of impinging water into the jets array to optimize the cooling rate in terms of local and average boiling heat transfer over the quenching surface.
) enhances to the peak value and drops significantly in a shorter time with 2-row array compare to 1-row array in both approaches, which is a proof of improvement of cooling in term of quenching time duration with 2-row multiple array. In the 2-row array, higher heat transfer performance is obtained in the second approach where Uj decreases 50% while the quenching area is extended. In the study of various Do/d in hollow cylinder, author captured very similar trend of heat transfer variation over Af with 1-row and 2-row arrays. However, the time delay to onset of surface heat flux enhancement was reduced gradually and higher heat flux rate was achieved with smaller Do/d. It may be concluded that there is a tradeoff between the multiple array configuration and the flow rate of impinging water into the jets array to optimize the cooling rate in terms of local and average boiling heat transfer over the quenching surface.
3.2. Water Jet Flow Rate
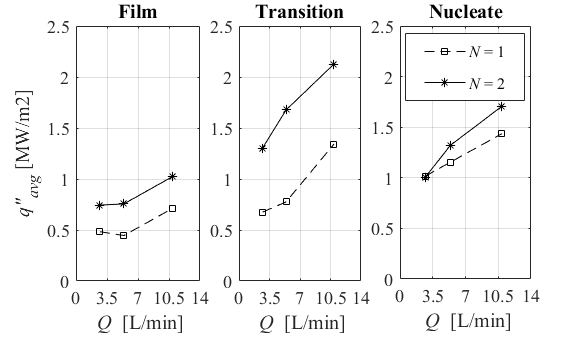
The rate of water flow from each individual impinging jet (Q) has been of interest in the local boiling heat transfer in previous studies. The result in Fig. 6(a) reveals that Q has noticeable influence on local boiling heat transfer, q"avg at xstg in all boiling regimes; higher Q enhances q"avg monotonically in 1-row and 2-row multiple arrays in good agreement with similar reported behavior in quenching rotary cylinder (Do/d = 12) by 1-row array [19].
(a)
(b)
Noticeable result is obtained by looking into effect of pitch and jet flow rate while Qtotal remains constant. Increased number of rows in pitch N = 2 enhances q"avg by an average 90% compared to 45% by two times more Q in 1-row array at xstg in the transition regimes. But in the nucleate boiling strong effect of pitch vanishes and the enhancement of average heat flux becomes 10% by greater N compared to 19% by two times Q in 1-row array. These values become 56% and 27% enhancement by N and Q respectively in the film boiling. This result reveals two times more effect of pitch than Q in the film and transition boiling and less effect in the nucleate boiling regime. Result in Fig. 6(b) shows higher jet flow rate increases q"MHF at xstg in both arrays and this is in agreement with the result of single jet experiment [16]. Temperature corresponding to MHF increases by higher Q in the 1-row array. This is caused by higher jet flow rate which creates shoulder of flux [22] in the transition boiling and therefore MHF occurs at higher temperature in the boiling curve. The TMHF is effected differently where higher Q has little effect to move the MHF point toward lower temperature in boiling curve. The time to reach MHF point (tMHF) decreases drastically by higher jet flow rate in both arrays of jets. The reduction in the time becomes more pronounced in the 1-row jets due to creation of shoulder of flux in transition boiling by higher Q which leads to shorter time to reach MHF at xstg. In agreement with the result in section 3.1, the result shows more dominant influence of multiple array than single jet flow rate (Q) in the local boiling heat transfer.
3.3. Water Subcooling
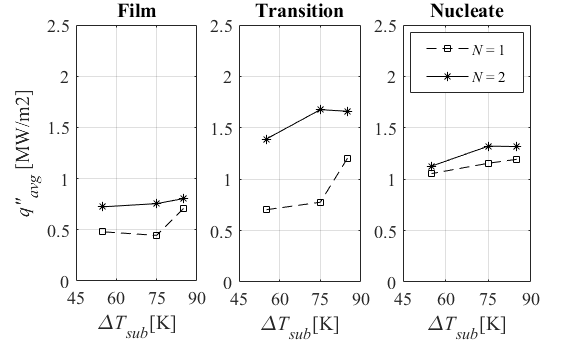
Fig. 7(a) presents result of investigation on q"avg at xstg influenced by water subcooling (∆Tsub). In the general trend, a slight increase is seen on local average heat flux in the film boiling. In the transition regime, dependency of q"avg on subcooling is observed more clearly; enhancement of q"avg by higher ∆Tsub is more pronounced in 75 ≤ ∆Tsub in 1-row array. Similar to the film boiling, slight enhancement is captured in the nucleate boiling by subcooling in both impingement arrays. The different behavior of q"avg in the boiling regimes is in agreement with previous study on single jet by Gradeck, et al. [23] and 1-row array by Jahedi and Moshfegh [19]. In the study of multiple jet array shown in Fig. 7(a), one can notice that enhancement of q"avg is significant in the film and transition boiling regimes, but little increase is captured in the nucleate regime by N = 2.
(a)
(b)
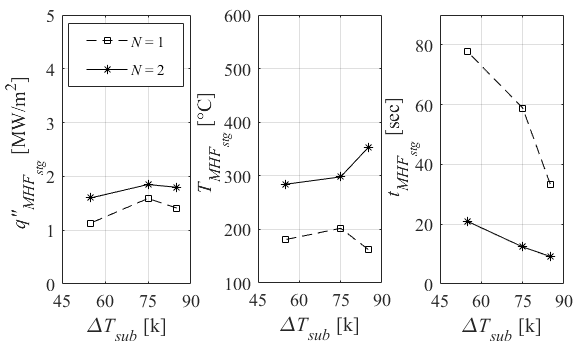
In the study of subcooling influence on maximum local heat transfer, Fig. 7(b) shows higher ∆Tsub increases heat flux in agreement with reported result of quenching rotary cylinder by single and 1-row arrays water jet [16, 19]. Enhancement of q"MHF by higher Qtotal in 2-row pitch again explains the importance of total flow rate and multiple jet configuration on the local boiling heat transfer. The temperature corresponding to MHF remains nearly at low level in 1-row array while TMHF is increased by higher subcooling in 2-row array. This interesting result shows that higher subcooling and Qtotal move the position of MHF toward higher temperatures in the boiling curve. The propagation velocity of WF is decreased gradually by lower subcooling [24] and this means that the stagnation point experiences the boiling regimes for a longer time by lower subcooling, causing increase of TMHF. It is interesting to see that higher Qtotal in 2-row array suppresses the TMHF severely compared to 1-row pitch.
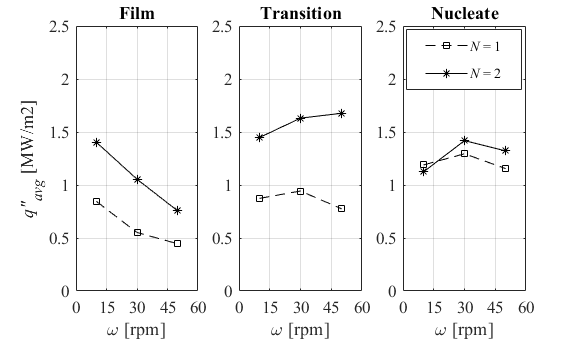
3.4. Rotation Speed
The new parameter in the hydrodynamic phenomena of boiling in presence of rotary test specimen is rotation speed of the cylinder (ω) corresponding to surface moving speed. Lower rotation speed interacts less with the wetted and wetting front zone and disturbs the hydraulic jump of WF less in each cycle of revolution. Surface also experiences longer cooling time under wetted and wetting front zone, but on the other hand, time to pass the dry zone is also greater in each revolution and lower passing frequency through the wet zone is obtained. Higher heat transfer is achieved in prior revolutions by less disturbed water flow over surface and longer time to pass wet zone in lower ω in the film boiling regime, see Fig. 8(a). In the transition boiling, heat transfer variation is little in 1-row pitch and becomes less at both small and large rotation speeds. Added extra row of nozzles in 2-row array extends the wet zone over Af and higher ω shorten the time for surface to approach the wet zone on the next revolutions. And these two parameters may damp the negative effect of water flow agitation by higher ω in the transition boiling and increase the heat transfer slightly. Similar behavior is captured by both arrays on heat transfer result in the nucleate boiling regime; both multiple jets arrays provided higher q"avg in the mid-range rotation speed (ω= 30 rpm) which may be due to less negative interaction effects of both high and low revolution speeds at this speed level. Comparing result of 1-row and 2-row arrays at q"avg in various rotation speeds shows significant increase of q"avg by larger N in the multiple jet array in the film and transition regimes in the presence of rotation speed variation and unaffected local heat transfer at xstg in the nucleate boiling.
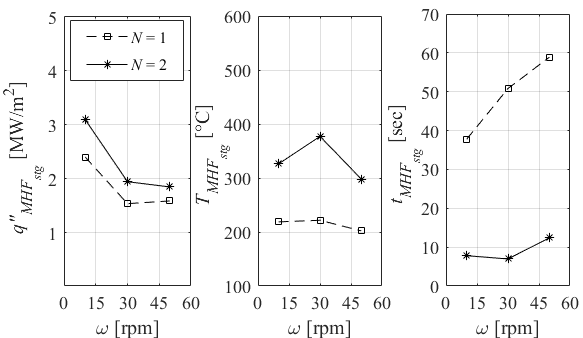
The result in Fig. 8(b) presents significant effect of ω on the MHF parameters. As discussed above, higher heat transfer is achieved at lower rotation speed by longer time of passage through wetted zone and cooling by less disturbed water impinging jets in prior revolutions. As a result, greater MHF occurs in shorter time (tMHF) in both arrays of nozzles. The variation of TMHF shows higher frequency of passing the wet zone at higher rotation speed shifts MHF point into smaller temperature slightly for ω > 30 rpm in the boiling curve at xstg in both pitches.
(a)
(b)
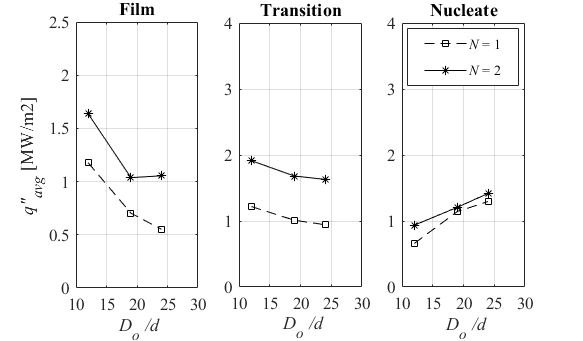
3.5. Curvature Ratio and Solid Thickness
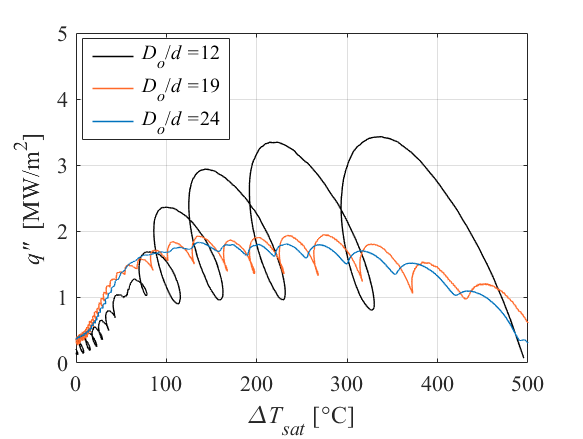
The curvature ratio (Do/d) is defined based on ratio between cylinder and jet size and since Di is dependent on Do in this study, bigger cylinder has larger thickness. In the film boiling regime, higher heat flux is seen by smaller hollow cylinders (Fig 9(a)). By investigation of boiling curves in Fig 9(b), it is found that magnitude of heat flux enhancement is stronger in film boiling with smaller Do/d. In the transition regime, a similar trend is seen with Do/d for smaller cylinder sizes. In the nucleate boiling regime at xstg, average heat flux is enhanced by larger Do/d, in general trend which it may be due to the fact that more mass in cylinder with larger Do/d transfers more heat flux toward surface when surface experiences nucleate boiling. In general, 2-row pitch raises magnitude of heat flux over Af in the film and transition boiling, and nucleate boiling regime appears unaffected by multiple jet array.
In the study of local maximum heat flux, authors found q"MHF and TMHF decreases with larger Do/d and the time corresponding to MHF point increases generally. The result showed that pitch N = 2 enhances MHF characteristics compared to N = 1. The stagnation point’s boiling curve at different cylinder sizes in Fig 9(b) shows clearly the cyclic variation of heat flux and temperature in revolutions by passing wetted and dry zones is suppressed with larger Do/d. This is because size of quenching area and thickness of hollow cylinder become larger with greater Do/d.
(a)
(b)
5. Conclusions
This paper presented an experimental study of quenching rotary hollow cylinder by 1-row and 2-row multiple water impinging jet arrays. The focus of the study was to investigate some important parameters on local and area-averaged heat transfer as well as understanding effect of multiple array configuration on boiling heat transfer in relation to jet’s water flow rate and the array’s total water flow rate. The results showed that water jet’s flow rate and curvature ratio of cylinder had significant effect on the average local heat transfer in the all boiling regimes at stagnation point of water impinging jet. Rotation speed influenced the average local heat transfer in the film and transition boiling regime. However significant effect of subcooling was found in the transition boiling regime. In study of local maximum heat flux (MHF) during quenching, results showed that higher water flow rate, subcooling and larger number of rows in array enhances MHF characteristics (higher heat flux and temperature and less time to reach the MHF). Lower rotation speed and smaller curvature ratio also provided similar effect on MHF parameters.
The effect of pitch combined with other parameters was highly pronounced in the film and transition boiling than in the nucleate boiling regime. It was found that for the constant total flow rate case, there is a trade-off between number of rows in the array (N) and water flow rate in terms of local and average surface heat transfer performance. The result also revealed higher heat transfer performance with constant total flow rate and larger N in the array compare to constant jet’s flow rate and larger N in the multiple array.
Acknowledgements
The authors acknowledge financial support by Swedish Energy Agency, Sweden’s Innovation Agency Vinnova, Ovako Company (Hofors, Sweden) and University of Gävle, Sweden. The authors are thankful for the assistance received by personnel at the laboratory of University of Gävle, Sweden.
References
[1] A. K. Mozumder, M. Monde, and P. L. Woodfield, "Delay of wetting propagation during jet impingement quenching for a high temperature surface," International Journal of Heat and Mass Transfer, vol. 48, no. 25–26, pp. 5395-5407, 12// 2005. View Article
[2] N. Hatta, J.-i. Kokado, and K. Hanasaki, "Numerical Analysis of Cooling Characteristics for Water Bar," Transactions of the Iron and Steel Institute of Japan, vol. 23, no. 7, pp. 555-564, 1983. View Article
[3] N. Karwa, T. Gambaryan-Roisman, P. Stephan, and C. Tropea, "Experimental investigation of circular free-surface jet impingement quenching: Transient hydrodynamics and heat transfer," Experimental Thermal and Fluid Science, vol. 35, no. 7, pp. 1435-1443, 10// 2011. View Article
[4] N. Karwa, L. Schmidt, and P. Stephan, "Hydrodynamics of quenching with impinging free-surface jet," International Journal of Heat and Mass Transfer, vol. 55, no. 13–14, pp. 3677-3685, 6// 2012. View Article
[5] H. Robidou, H. Auracher, P. Gardin, and M. Lebouché, "Controlled cooling of a hot plate with a water jet," Experimental Thermal and Fluid Science, vol. 26, no. 2–4, pp. 123-129, 6// 2002. View Article
[6] C. Agrawal, R. Kumar, A. Gupta, and B. Chatterjee, "Effect of jet diameter on the maximum surface heat flux during quenching of hot surface," Nuclear Engineering and Design, vol. 265, pp. 727-736, 2013. View Article
[7] C. Agrawal, R. Kumar, A. Gupta, and B. Chatterjee, "Effect of jet diameter on the rewetting of hot horizontal surfaces during quenching," Experimental Thermal and Fluid Science, vol. 42, pp. 25-37, 2012. View Article
[8] B. Wang, X. Guo, Q. Xie, Z. Wang, and G. Wang, "Heat transfer characteristic research during jet impinging on top/bottom hot steel plate," International Journal of Heat and Mass Transfer, vol. 101, pp. 844-851, 2016/10/01/ 2016. View Article
[9] A. K. Mozumder, M. Monde, P. L. Woodfield, and M. A. Islam, "Maximum heat flux in relation to quenching of a high temperature surface with liquid jet impingement," International Journal of Heat and Mass Transfer, vol. 49, no. 17–18, pp. 2877-2888, 8// 2006. View Article
[10] T. Kim, D.-W. Oh, K. H. Do, J. M. Park, and J. Lee, "Effect of Initial Temperature of a Cylindrical Steel Block on Heat Transfer Characteristics of Staggered Array Jets During Water Jet Quenching," Heat Transfer Engineering, vol. 36, no. 12, pp. 1037-1045, 2015/08/13 2014. View Article
[11] K. Morisawa, J.-y. Nakahara, K. Nagata, H. Fujimoto, T. Hama, and H. Takuda, "Boiling Heat Transfer Characteristics of Vertical Water Jet Impinging on Horizontally Moving Hot Plate," ISIJ International, vol. 58, no. 1, pp. 140-145, 2018. View Article
[12] M. Gradeck, A. Kouachi, A. Dani, D. Arnoult, and J. Borean, "Experimental and numerical study of the hydraulic jump of an impinging jet on a moving surface," Experimental thermal and fluid science, vol. 30, no. 3, pp. 193-201, 2006. View Article
[13] S. Vakili and M. S. Gadala, "Boiling heat transfer of multiple impinging jets on a hot moving plate," Heat Transfer Engineering, vol. 34, no. 7, pp. 580-595, 2013. View Article
[14] M. A. Kumar, M. Yuichi, and M. Masanori, "Experimental Study of Heat Transfer for a Rotating Cylinder Water Jet Impingement Quenching," Journal of Energy and Power Engineering, vol. 7, pp. 411-422, 2013.
[15] M. Jahedi, F. Berntsson, J. Wren, and B. Moshfegh, "Transient inverse heat conduction problem of quenching a hollow cylinder by one row of water jets," International Journal of Heat and Mass Transfer, vol. 117, pp. 748-756, 2// 2018. View Article
[16] S. Tsuboyama, T. Higashi, Y. Mitsutake, S.B. Illias, A. Mazumder, K. Tsubaki, M. Monde, "Characteristics of Transient Heat Transfer and Wetting Phenomena During Laminar Jet Quenching on Rotating Cylinder," Procedia Engineering, vol. 105, no. Supplement C, pp. 787-797, 2015/01/01/ 2015. View Article
[17] A. K. Mozumder, Y. Mitsutake, and M. Monde, "Subcooled water jet quenching phenomena for a high temperature rotating cylinder," International Journal of Heat and Mass Transfer, vol. 68, no. 0, pp. 466-478, 1// 2014. View Article
[18] M. Jahedi and B. Moshfegh, "Experimental study of quenching process on a rotating hollow cylinder by onerow of impinging jets," in 9th World Conference on Experimental Heat Transfer, Fluid Mechanics and Thermodynamics , Brazil, 2017, vol. 9, 2017.
[19] M. Jahedi and B. Moshfegh, "Quenching a rotary hollow cylinder by multiple configurations of water-impinging jets," International Journal of Heat and Mass Transfer, vol. 137, pp. 124-137, 2019/07/01/ 2019. View Article
[20] S. Slayzak, R. Viskanta, and F. Incropera, "Effects of interaction between adjacent free surface planar jets on local heat transfer from the impingement surface," International journal of heat and mass transfer, vol. 37, no. 2, pp. 269-282, 1994. View Article
[21] Y. Saad, Iterative methods for sparse linear systems. siam, 2003. View Article
[22] D. E. Hall, F. P. Incropera, and R. Viskanta, "Jet impingement boiling from a circular free-surface jet during quenching: Part 1—single-phase jet," Journal of heat transfer, vol. 123, no. 5, pp. 901-910, 2001. View Article
[23] M. Gradeck, A. Kouachi, M. Lebouché, F. Volle, D. Maillet, and J. L. Borean, "Boiling curves in relation to quenching of a high temperature moving surface with liquid jet impingement," International Journal of Heat and Mass Transfer, vol. 52, no. 5–6, pp. 1094-1104, 2// 2009. View Article
[24] P. L. Woodfield, A. K. Mozumder, and M. Monde, "On the size of the boiling region in jet impingement quenching," International Journal of Heat and Mass Transfer, vol. 52, no. 1–2, pp. 460-465, 1/15/ 2009. View Article

