Journal of Fluid Flow, Heat and Mass Transfer (JFFHMT)

ISSN: 2368-6111

1. Introduction

Heating Ventilation and Air-conditioning (HVAC) systems account for 55% and 65% of the total energy and greenhouse gas emissions in the building sector of North America [1]. It is predicted that the global cooling energy demand will increase by 30 times towards the end of this century [2]. Therefore, recent HVAC systems incorporate air-to-air energy exchangers to reduce their energy consumption. Air-to-air energy exchangers condition the supply air by utilizing the energy of exhaust air and hence, reduces the load and size of HVAC systems.

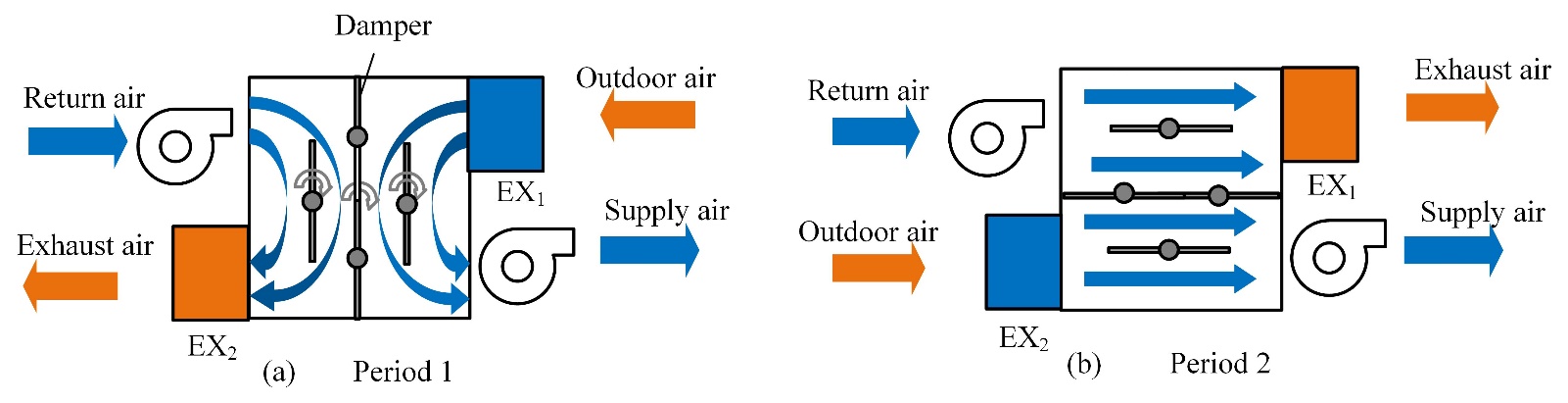
Fixed-bed regenerators are recently introduced in HVAC systems due to their inherent advantages such as the high heat transfer effectiveness and fewer moving components as compared to rotary regenerators [3],[4]. The schematic of an FBR with two stationary exchangers (EX₁ and EX₂ ), two fans, and a damper assembly is shown in Figure 1. One complete cycle of FBR can be divided into two recovery periods. During the first half of the operation (period 1), the dampers are positioned vertically, as shown in Figure 1(a). During summer (hot outdoor air), EX₁ stores the heat from the outdoor air and simultaneously, EX₂ releases the heat stored in the previous period to return air. At the end of period 1, the dampers rotate 90°. During period 2 (EX₂ stores the heat from the outdoor air and EX₁ releases the heat stored in the previous period to return air. The duration of each period is about 60 seconds [5] and the two periods repeat alternatively to deliver conditioned outdoor air continuously to the building.

Each stationary exchanger located in FBR consists of stacks of metallic plates to store and exchange the heat between hot and cold airstreams (i.e., outdoor and indoor air). The use of corrugated plates in exchangers is considered as an effective way for heat transfer enhancement. The corrugations in the plates increase the heat transfer area and generate turbulence even at low Reynolds numbers. Numerous studies have been reported addressing the heat transfer enhancement and pressure drop penalty in heat exchangers having corrugated plates [6],[7],[8]. Heat transfer correlations for various standard geometries such as circular [9], flat plate or sinusoidal flow channels [10] with corrugations are available in the literature. However, these correlations are only valid for specific ranges of operating conditions and a given geometry.

There are only a few experimental studies explaining the performance improvement of regenerators by altering the plate geometry [11],[12] and especially, none of them were focussed on HVAC applications. The available parametric studies in FBRs are limited due to the practical challenges for testing such as high volume of conditioned airflow, transient measurements, large laboratory space, and need of full-scale FBRs [13]. Therefore, a new testing methodology for FBRs is introduced, known as small-scale testing, which is developed and validated in our earlier study [4]. The small-scale methodology eliminates the challenges in full-scale testing and enables researchers to perform experiments for a wide range of operating conditions. This small-scale testing facility is used in the present study to evaluate the performance of corrugated plate FBR. Results from the present study will be useful for HVAC designers to develop FBRs with high effectiveness.

Methodology

This small-scale testing facility is used to evaluate the performance of corrugated plate FBR as explained earlier in the introduction. However, the performance of the parallel plate FBR is estimated using a validated numerical model. Kays and London's correlation [14] is used in the present study to develop a correlation for the heat transfer coefficient of corrugated plate FBR. The test facility, FBR specifications, numerical model, and Kays and London correlation are explained briefly in the following subsections.

2. 1. Test Facility

The test facility consists of two air lines and a test section as shown in Figure 2. Each airline consists of a blower which supplies the required flow rate to the test section. The flow rate of each air stream to the test section is varied by adjusting the blower rotation using a variable voltage transformer and measured using an orifice plate and a differential pressure transducer (model: Validyne DP 17). One of the airstreams is heated to 38°C using a PID controlled tubular heater while the other stream is kept at room temperature. The test section (in which FBR is placed) slides between the two airstreams using a set of linear actuators. FBR stores the heat from the hot air stream during the first half of its operation (hot period) and transfers to the cold air stream during the next half (cold period). The temperatures of both the airstreams at the inlets and outlets of FBR are measured using calibrated T-type thermocouples. The maximum uncertainty in the temperature and flow rate measurements are ±0.2°C and ± 4%, respectively. A detailed description of the test facility, calibration, data acquisition and analysis procedure are already reported in the earlier study of the authors [4].

2.2 Fixed Bed Regenerators

The physical and geometrical properties of both FBRs are listed in Table 1. The corrugated FBR is supplied by Tempeff North America, Canada, and consists of stacked metal plates with a proprietary corrugation profile.

The heat transfer performance of FBRs is quantified using sensible effectiveness (Eqn. 1), which is defined as the ratio of the actual heat transfer rate between the airstreams to the maximum possible heat transfer rate [14].

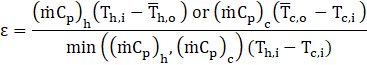
where and T are the heat capacity rate and the temperature of hot/cold air streams, respectively and suffixes h, c, i, and o represent the hot, cold, inlet and outlet air conditions, respectively. The outlet temperatures of air streams in both the FBR vary with time and therefore, the sensible effectiveness of a hot or cold period is calculated using time averaged outlet temperatures over the entire period. Detailed analysis of temperature measurements and effectiveness determination of FBR are explained in the earlier literature [4], [15], [16].

Pressure drop is also an important performance parameter of the flow passages. The pressure drop is reported using non-dimensional friction factor correlation [17], as presented in Eqn. 2.

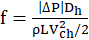
Table 1. Geometrical details and thermophysical properties of FBRs

Sl. No	Configuration	Channel				Plates
		Length (mm)	Width (mm)	Hydraulic Diameter (mm)	Height (mm)	Thermal conductivity (W/m·k)	Density (kg/m3)	Specific heat (J/kg·K)
1	Parallel-plate	200	80	8.16	4	2730	220	904
2	Corrugated-plate	210	83.8	8.18	4	2730	220	904

2.3. Numerical Model

A 1-D numerical model is also used in this study to predict the performance of the FBR. In the case of parallel plate FBR, the air flow inside the exchanger is assumed to be laminar and incompressible since the Reynolds numbers are less than 2000. The heat transfer process is modeled using the bulk mean temperature of the air. The correlation of average heat transfer coefficient derived from the small-scale experiments is used to model the heat transfer process inside the corrugated FBR. The governing energy equations which include energy storage, convection and conduction in the air flow (subscript ‘g’) and matrix (subscript ‘m’) are as follows [3], [18];

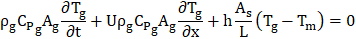
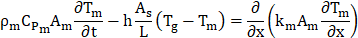
Where: T, x, ρ, C_p, k, U, h, L and t are temperature, axial coordinate, density, specific heat capacity, thermal conductivity, mean airflow velocity, convective heat transfer coefficient, length of channel and time, respectively. The cross-sectional area of the channel, heat transfer surface area and cross-sectional area of the exchanger sheet are denoted by A_g,A_s and A_m.

Appropriate boundary conditions are also implemented to solve the governing equations. Assumptions and solving procedures of the numerical model are explained in Ref [3], [18].

2.4. Kays and London Correlation

Kays and London proposed an empirical correlation (Eqn. (5)) to determine the sensible effectiveness of regenerators by including two correction factors [14]. The correction factors account for the effects of the period and longitudinal conduction through the matrix.

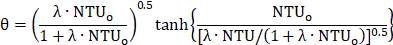
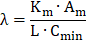
where NTU_o , Cr^*, Cr_min and λ are the number of transfer units, matrix heat capacity ratio, minimum heat capacity rate of fluid and longitudinal heat conduction factor, respectively. The correlation is valid when NTU_o and Cr ^* are higher than unity.

The NTU_o and Cr^* can be determined using Eqs. (8) and (9).

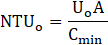
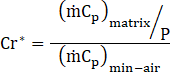
where U_o, and P represents the overall heat transfer coefficient and period of FBR The heat transfer coefficient for parallel plate FBRs is be determined using the following equation [19].

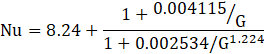
where Nu and G are Nusselt number and Gratez number, respectively.

3. Results and Discussion

The temperature profiles of the airstreams at FBRs outlets, sensible effectiveness and heat transfer coefficients of the parallel and corrugated plate FBRs are presented in this section. The tests were performed at balanced flow conditions . The specific test conditions are listed in Table 2.

Table 2. Tested operating conditions of corrugated and parallel plate FBRs

Air flow rate (L/s)	Face velocity (m/s)	Re	Period (seconds)
5-14	0.85-2.43	500-1450	15, 30, 45, 60

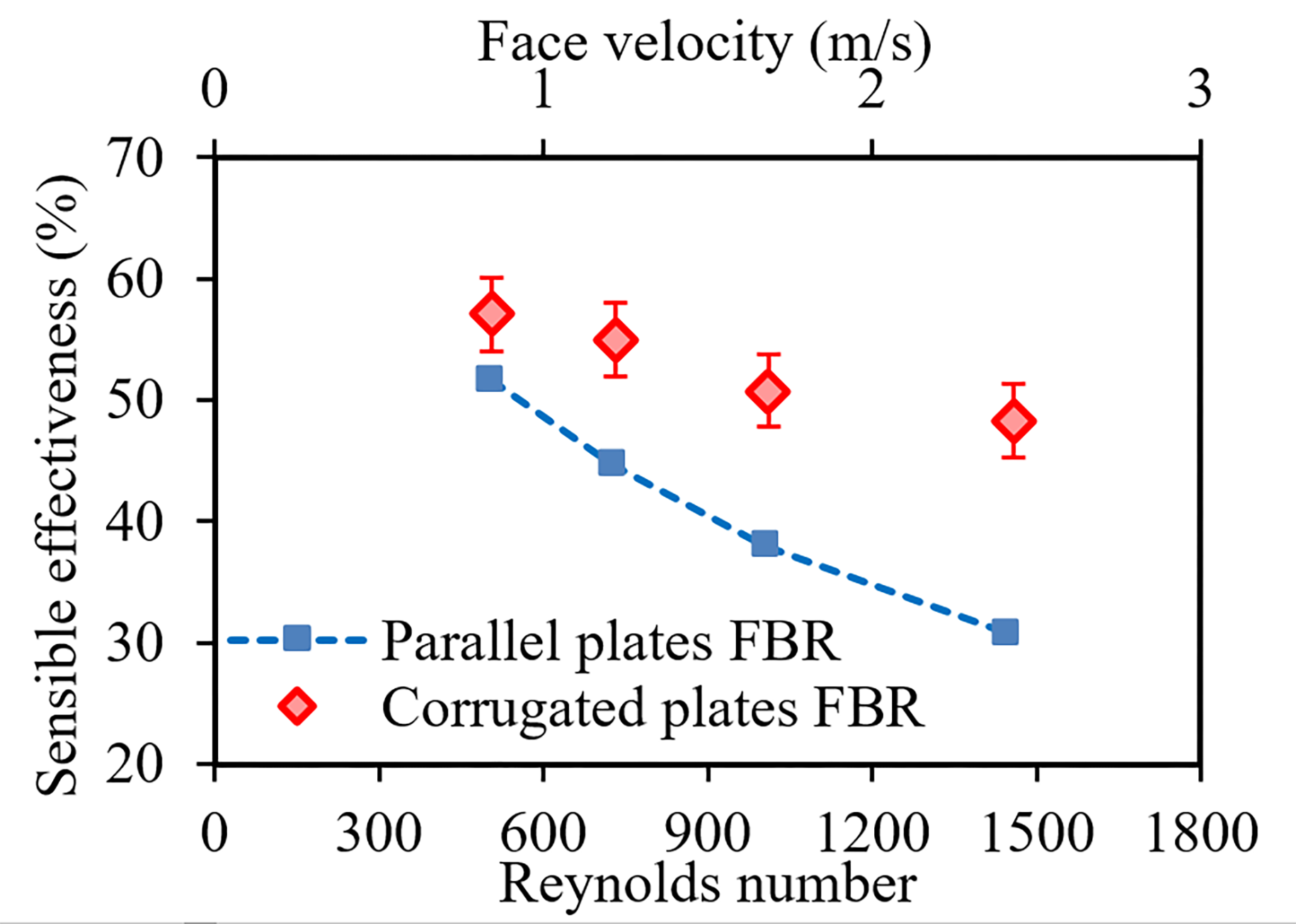
The sensible effectiveness of corrugated plate FBR is compared with that of the parallel plate FBR and the comparison is shown in Figure 3. The effectiveness of corrugated plate FBR is 18% higher than that of parallel plate FBR (Re =1450). This is due to enhancement in the (i) heat transfer coefficient and (ii) increase heat transfer area by the corrugation. For the tested conditions mentioned in Table-2, an area change of 9% can improve only a maximum of 2% sensible effectiveness. Therefore, the effect of heat transfer coefficient is significant, and which is studied in detail.

For the case of parallel plate FBR, the flow through the exchanger must be laminar since Re is less than 2000. Hence, Eqn. (9) is used to determine the average heat transfer coefficient of parallel plate FBR. The procedure for calculating the heat transfer coefficient of corrugated plate FBR is as follows. (i) NTU_o is calculated using the effectiveness determined from experiments (period = 30 s) and Kays and London correlation (Eqn. (5)) the heat transfer coefficient is determined from Eqn. 8 using the heat transfer area of plates and mass flow rate of the air streams. Figure 4 shows the comparison between the heat transfer coefficients of corrugated and parallel plate FBRs. The uncertainties in experimental effectiveness arises from the temperature and mass flow rate measurements. The method of uncertainty evaluation of sensible effectiveness in small tests and numerical model is discussed in detail in Ref [4] [20].

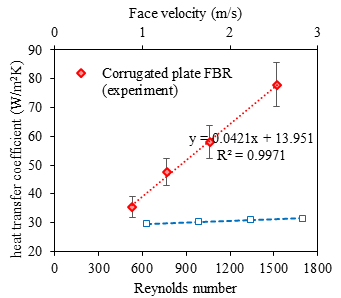
At low face velocities, both the FBRs are having similar heat transfer coefficient values. With an increase in face velocity, the heat transfer coefficient increases significantly for corrugated plate FBR. This is due to its corrugations which leading to the formation of vortices in the flow channel. As a result of vortices, the thermal boundary layer gets disturbed continuously which enhances the mixing of fluid layers. This continuous mixing increases the heat transfer coefficient. It is observed from Figure 4 that the heat transfer coefficient of corrugated plate FBR is 150 % higher than that of parallel plate FBR at the face velocity of 2.5 m/s. In addition, it is found that the heat transfer coefficient of corrugated plate FBR increases about three times of the initial value, whereas it is nearly constant for the entire range in case of parallel plate FBR.

A correlation for heat transfer coefficient in corrugated plate FBR is derived as a function of Reynolds number and is shown below.

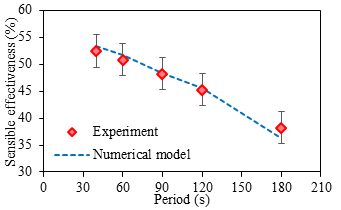
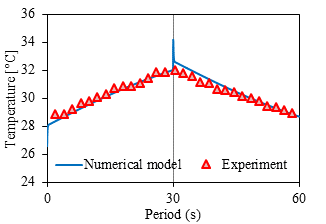
Eqn. 11 is used in the numerical model to evaluate the effectiveness of corrugated plate FBR at different recovery periods. The comparison of sensible effectiveness from experiments and numerical model is shown in Figure 5. The maximum difference in sensible effectiveness is 2% at a period of 90 s. The reason for this deviation includes the uncertainty in experimental measurements and heat loss/gain of the test section with the surrounding. The temperatures of air streams at the outlet of FBRs from the experiment and the numerical model are also compared and shown in Figure 6. The developed correlation for the heat transfer coefficient from this small-scale experimental facility is valid for the practical FBR units having NTU_o ranging from 5-8 and the same range of Re.

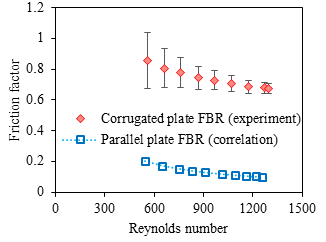
It is necessary to evaluate the pressure drop as it influence the fan energy consumption and thereby, deciding the usefulness of corrugated plate in FBR. The friction factor of corrugated plate and parallel plate FBRs is evaluated from the pressure drop measurements and is shown in Figure 7. The friction factor of corrugated FBR is nearly six times higher than that of parallel plate FBR. However, selecting corrugated FBRs will be beneficial since it has high sensible effectiveness and requires less exchanger material (results in reduction overall size of the exchanger) compared to parallel plate FBR. More studies will be conducted in future to determine the optimum corrugation angle and corrugation depth for achieving maximum sensible effectiveness with minimum pressure drop across the exchanger.

4. Conclusion

The sensible effectiveness of fixed-bed regenerators (FBR) having corrugated, and parallel plates is determined using a small-scale test facility and a numerical model respectively. Experiments and numerical simulations were performed at Reynolds numbers (Re) ranging from 500 to 1450. The results show that the heat transfer coefficient, sensible effectiveness and friction factor of the corrugated plate FBR are higher than that of the parallel plate FBR. It is found that the heat transfer coefficient of corrugated plate FBR increases three times when Re increased from 500 to 1450. However, the friction factor of corrugated plate FBR is nearly six times that of parallel plate FBR. A correlation for the heat transfer coefficient of corrugated plate FBR is derived and evaluated the sensible effectiveness at different operating conditions using a numerical model.

Acknowledgments

Financial support from the College of Engineering and Postdoctoral Studies of the University of Saskatchewan, National Science and Engineering Research Council (NSERC) and Tempeff Inc., Winnipeg are appreciated. Technical supports provided by Hayden Reitenbach and Shawn Reinink (Laboratory managers, Thermal and Fluids laboratory, University of Saskatchewan) are also appreciated.

References