Volume 8 - Year 2021 - Pages 14-22
DOI: 10.11159/jffhmt.2021.003
Numerical and Experimental Analysis of Properties and Performance of Solar Stills
Ghaleb Ibrahim1 and Husham M. Ahmed2
1Associate Professor, 2Professor
1American University of Dubai, School of Engineering,
Dubai, United Arab Emirates
1gibrahim@aud.edu
2AMA International University Bahrain, College of Engineering, Kingdom of Bahrain
2hmahmed@amaiu.edu.bh
Abstract - Potable water not only is important for life but also for industrial and agricultural purposes. For many decades, the problem of water shortage has been one of the main challenges facing the world. Solar distillation is regarded by many investigators as one of the important methods to solve water scarcity problems. A solar still is a simple device which can be effectively used to convert saline water into fresh water. The productivity depends on many parameters, which among them are transmittance of the cover, thermal properties of the basin and water, and heat loss through the solar still. In this research, the effect of three design parameters (basin heat transfer coefficient, glass absorptivity and glass transmissivity) on performance of the conventional solar still was theoretically investigated and compared with experimental results. Iteration was necessary to obtain the values of the design parameters that produce good matching between the theoretical and experimental results. The effect of overall heat transfer coefficient Ub found to be significantly large especially at low values. It was found that reducing the overall heat transfer coefficient from 30 to 0.0 W/m2K will increase the production rate by 64.02% and solar still efficiency will also increase accordingly. It was also found that reducing the absorptivity from 0.1 to 0.01 will increase the solar still efficiency by 23.28%.. The results showed that the solution is highly sensitive and depending on the precision of these parameters. It can be concluded that an accurate prior knowledge of these parameters is essential to obtain reasonable results. The experimental and theoretical hourly production rate are in good agreement at Ub = 5.9W/m2 K,αg=0.075 and τg=0.845 where the maximum discrepancy between them is 23% at around 14:00.
Keywords: Productivity; Solar stills; Water desalination; Wick materials;
© Copyright 2020 Authors - This is an Open Access article published under the Creative Commons Attribution License terms Creative Commons Attribution License terms. Unrestricted use, distribution, and reproduction in any medium are permitted, provided the original work is properly cited.
Date Received: 2020-11-14
Date Accepted: 2020-11-14
Date Published: 2021-01-21
1. Introduction
The available amount of fresh water on earth is very limited, and the demands are significantly increased all over the world due to the rapid population growth and considerable increasing trends of agricultural and industrial requirements. Fresh water reserves are continually decreasing. Industrial wastes and sewage discharges have polluted reserves and underground water. The availability of clean and pure drinking water has become one of the most urgent needs for human community in many countries mainly in the Middle East and North Africa. The majority of areas that have deficiencies in fresh water supply have huge amounts of solar energy freely available [1]-[2]. A solar still is a simple device, which can be effectively used to convert saline water into fresh water. The enhancement of solar stills performance and improving their production capacity of distilled water are the main goals of the investigators in recent years [3].The need for a small-scale solar distillation unit increases continuously, especially in arid regions where sunshine is abundant and fresh water is scarce. These devices are suitable for a single house or a small community for providing good quality of drinking water [4].
In order to have a clear idea about energy efficiency, it is convenient to study heat loss of the solar still. Thermal losses mainly occur through the glass cover by radiation and convection heat transfer to the ambient and through the bottom of the basin plate via the insulation by conduction and convection of heat transfer to the ambient. A prior knowledge of the outcome form solar still using theoretical model is of great importance to design and manufacture a solar still that meets the xpectation in terms of functionality and productivity [5].
Ref. [6] reported a comprehensive study of heat transfer, mass transfer, and entropy rate of humid air for a single solar still. They concluded that minimum glass thickness and decreasing thermal losses of the solar still (mainly due to heat loss through the basin plate to the ambient) are the best operating parameters that give maximum solar still productivity. Ref. [7] studied the effect of parameters on the performance of solar stills. They found that productivity is largely affected by climatic, operational, and design parameters. Ref. [8] conducted a comprehensive energy analysis of a passive solar distillation system. Applying a set of typical design and operating parameters using a computer program, the temperatures of basin-liner, saline water body and inner and outer glass cover are estimated. They found that a 100% increase in insulation thickness of the passive solar still will increase the energy efficiency and daily yield by 5.33% and 5.52%, respectively. Similar results were reported by Ref. [6]. Ref. [9] compared different mathematical models to describe the simultaneous heat and mass transfer process inside solar stills. The results of these models showed a wide range of discrepancy for the estimation of the daily productivity and thermal efficiency of the solar still. Ref. [10] tabulated the simulation parameters used in their model such as transmitivity, emissivity, absorptivity, specific heat and density for the glass, water and basin plate and used as overall heat transfer coefficient of 14 W/m2K . The basin overall heat transfer coefficient used in various publications varied between 2.8 and 20 W/m2K. Although this parameter is of great importance in solar still, most of these works provided no justification or sufficient information with regard to insulation applied in their systems. Therefore, the physical and thermal properties of the insulation materials are important parameters in terms of the solution of theoretical model and so must be accurately known to guaranty reliable results. The transmittance and absorptance of a glass depend on the type and thickness of the glass in particular the angle that the incidence beam of light makes with the normal to the surface. Ref. [11] provided data for the absorption and transmission of thermal radiation by single and double glazed windows (with index of refraction n = 1.2). Ref. [12] studied the effect of glass thickness on performance of flat plate solar collectors for fruits drying. Their results showed that the change in glass thickness results into variation into collector efficiency. They concluded that the use of 4 mm glass thick improves the performance of air solar collector by 7.6% compared to 3, 5, and 6 mm and the 4 mm glass thickness gave optimal transmittance and convective losses, and hence is the best glazing thickness.
The theoretical modelling is necessary in engineering field. It enables researchers easily, relatively and without essential expenses to investigate the properties and behaviour of a system in any conceivable situation. A prior knowledge of the outcome form solar still using theoretical model is of great importance to design and manufacture a solar still that meets the expectation in terms of functionality and productivity. The present work is a theoretical study applied to solar stills to address the importance of the above-mentioned transmissivity, absorptivity, reflectance and the basin overall heat transfer coefficient and investigate their effect on the performance of the solar still.
The theoretical modelling is necessary in engineering field. It enables researchers easily, relatively and without essential expenses to investigate the properties and behaviour of a system in any conceivable situation. A prior knowledge of the outcome form solar still using theoretical model is of great importance to design and manufacture a solar still that meets the expectation in terms of functionality and productivity. The present work is a theoretical study applied to solar stills to address the importance of the above-mentioned transmissivity, absorptivity, reflectance and the basin overall heat transfer coefficient and investigate their effect on the performance of the solar still.
2. THEORETICAL MODELING OF SOLAR STILL
2.1. Principles of Solar Still
Solar radiation is partially reflected to the outside and partially absorbed by the glass cover and mostly it is transmitted through the glass cover to the water in the basin. The water in turn absorbs small portion of the received solar radiation and transmit the rest to the basin in conventional solar stills. The solar radiation absorbed by water and the heat gain by the water from the basin will raise the water temperature above that of the glass cover. This allows the evaporated water to condense on the glass cover surface. Inside the solar still the increase in water temperature causes the vapor pressure at the air water interface to increase above that in the bulk of the air. Thus, the water evaporates as a result of the vapor pressure difference and the air humidity in the tank rise and so its dew point. Since the glass cover temperature is lower than the dew point of the humid air, condensation occurs on the glass surface. The evaporated water must be compensated to keep the water level in the tank [13]-[15].
2.2. Thermal Analysis of the Solar Still
In this work, the model of Ref. [16] who used a time dependent energy balance on solar stills, which will be modified to fit the current work conditions. The theoretical model will be using the measured data of the solar intensity, ambient temperature and wind speed given in Ref. [17]. The solution will be conducted at various absorptivity, transmissivity and basin overall heat transfer coefficient. The operation of solar still is governed by the various heat and mass transfer modes occurring in the system. The major energy transport mechanism in the still is shown in figure 1. Applying the conservation of energy to the conventional solar still components, namely the glass cover, saline water and basin, the following three equations are obtained.
Energy gained by the glass cover (from sun and convective, radiative and evaporative heat transfer from water to glass) is equal to the summation of energy lost by radiative and convective heat transfer between glass and sky, and energy stored by glass.
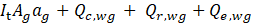
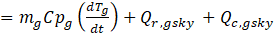

Where It is radiation intensity, A is surface area, a is the Absorptivity, Q is rate of heat transfer, m is mass, Cp is specific heat. The subscript r denotes radiation, g denotes glass and T is temperature, w denotes water, e denotes evaporation and c denotes convection.
Energy received by the saline water in the still (from sun and base) is equal to the summation of energy lost by (1) convective, radiative and evaporative heat transfer between water and glass, plus (2) the energy by the replaced cooler water that replaces the evaporated portion, (3) side wall loss and (4) energy stored by the saline water. The water reflectance is negligibly small.
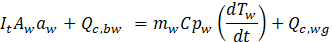
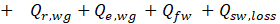
Where the subscript b denotes basin, fw denotes water feed, sw denotes side wall.
Energy received by the basin (from sun) is equal to the summation of energy (1) lost by convective heat transfer between basin and water, (2) heat lost from the bottom of the basin and (3) energy stored by the basin. It is assumed that all solar radiation reached the basin are absorbed by the basin with zero reflectance
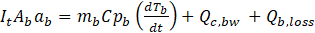
Where ![]() ;
;![]() ;
; ![]() .
. ![]() is the glass reflectance, τg is the glass transmittance.
is the glass reflectance, τg is the glass transmittance.
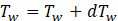
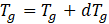
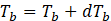
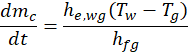
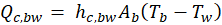
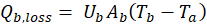
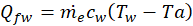
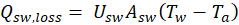
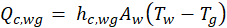
Where mc denotes mass of condensate, hfg is the enthalpy of evaporation at Tw, h is the heat transfer coefficient, U is the over all heat transfer coefficient.
Heat transfer between water and the glass cover: convective heat transfer coefficient is
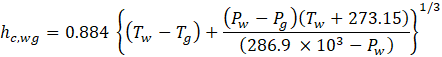
Where Pw is the partial pressure at Tw, Pg is the partial pressure at Tg.
The radiative heat transfers is
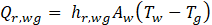
the radiative heat transfer coefficient
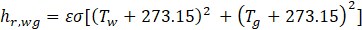
Where
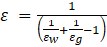
The rate of heat transfer due to evaporation is
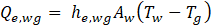
Where the evaporative heat transfer coefficient is
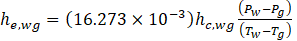
The radiative heat transfers between sky and the glass is
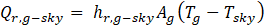
The radiative heat transfer coefficient is
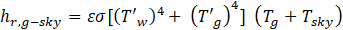
where where T'w=Tw+273 and T'g= Tg+273
The effective sky temperature is [16]-[18]
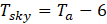
The convective heat transfers between sky and the glass is
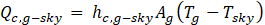
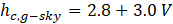
Where V is the wind velocity
Solar still efficiency may be calculated using equation 24.
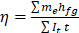
Where η solar still efficiency.
The daily average percentage of thermal heat loss through the basin to the ambient may be calculated relative to the radiation intensity using equation 25.
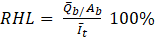
Where RHL is the relative heat loss, ![]() is the daily average rate of heat loss through the basin,
is the daily average rate of heat loss through the basin,![]() is the daily average radiation intensity
is the daily average radiation intensity
2.3. Bottom and sidewall heat transfer coefficients;
Since the solar still contents (basin plate, water and moist air) are at a higher temperatures than the ambient temperatures. A heat loss is expected to occur. Therefore the bottom and side wall are insulated. If the insulation is properly applied, the insulation thermal resistance will be dominant to other thermal resistances. However including all thermal resistance the overall heat transfer coefficient of bottom heat loss is obtained
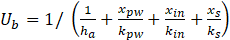
Where in the thermal resistance of the insulation ![]() is dominant. And the side wall
overall heat transfer coefficient is approximated by researcher [9, 19, 20] as
is dominant. And the side wall
overall heat transfer coefficient is approximated by researcher [9, 19, 20] as
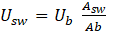
Some researchers embedded the side heat transfer coefficient in the Ub. In this case a value of 14 W/m2 K [15] and 20 W/m2 K[7] were used. Ref. [21] took the side wall heat transfer coefficient as 0.5 W/m2K. In this current work the side wall heat loss is obtained as
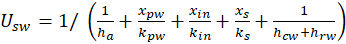
SWhere hcw = hc,wg and hrw = h(r,wg). These coefficients are time dependent. x thickness of plywood, k thermal conductivity, the subscript, pw is ply wood and in is insulation and s is galvanized steel.
3. RESULTS AND DISCUSSIONS
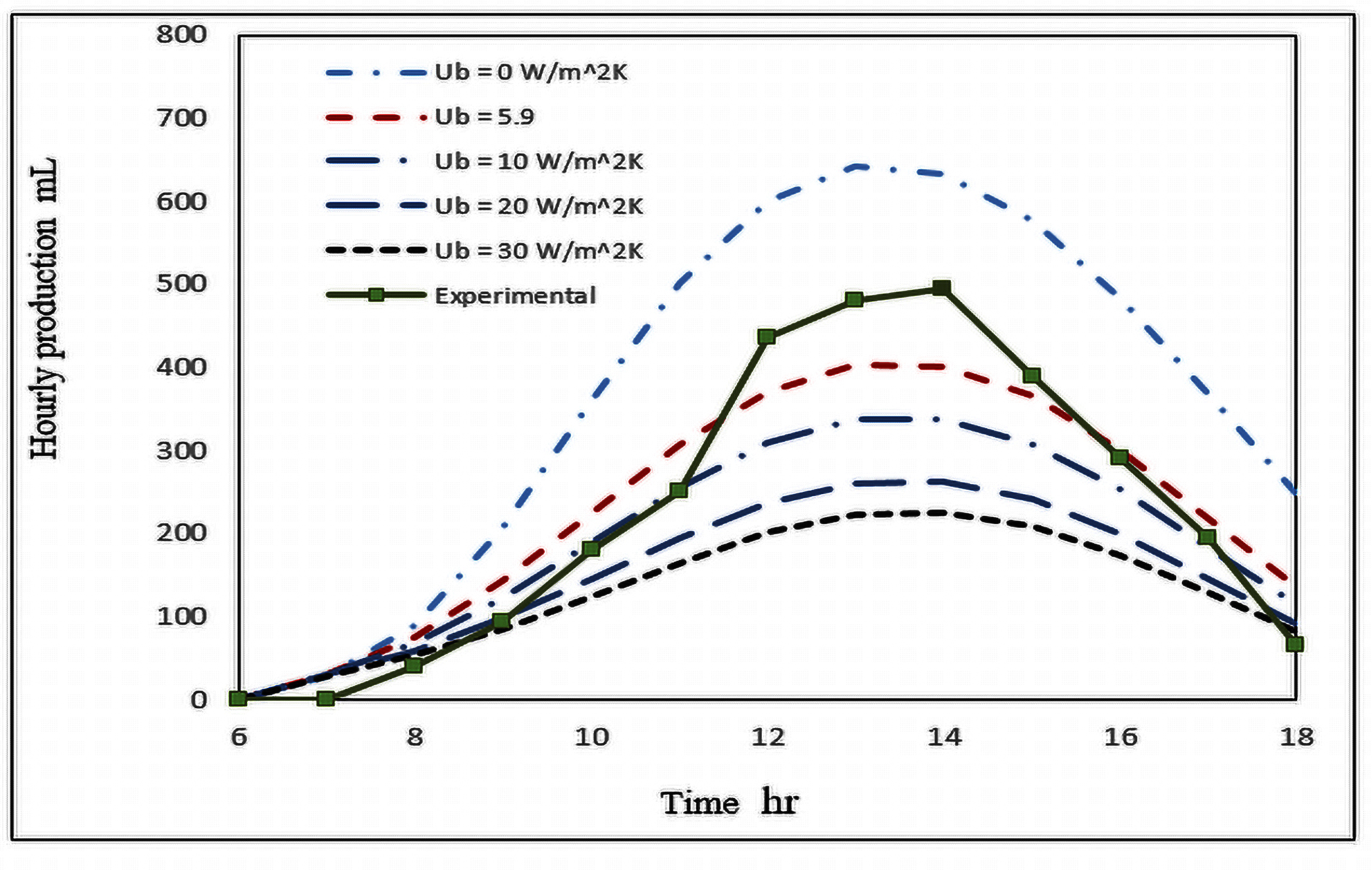
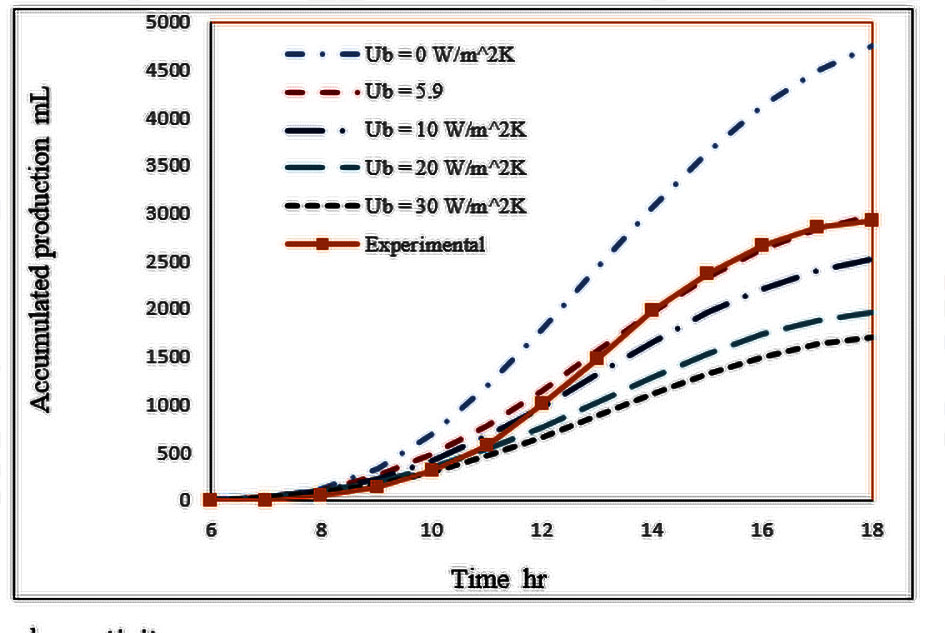
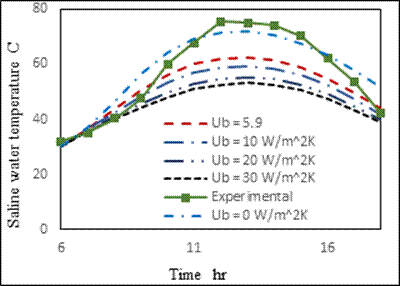
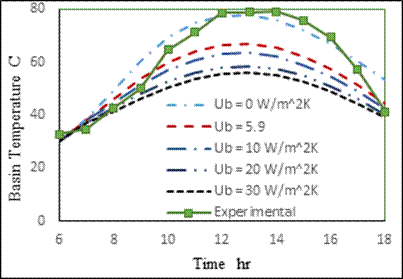
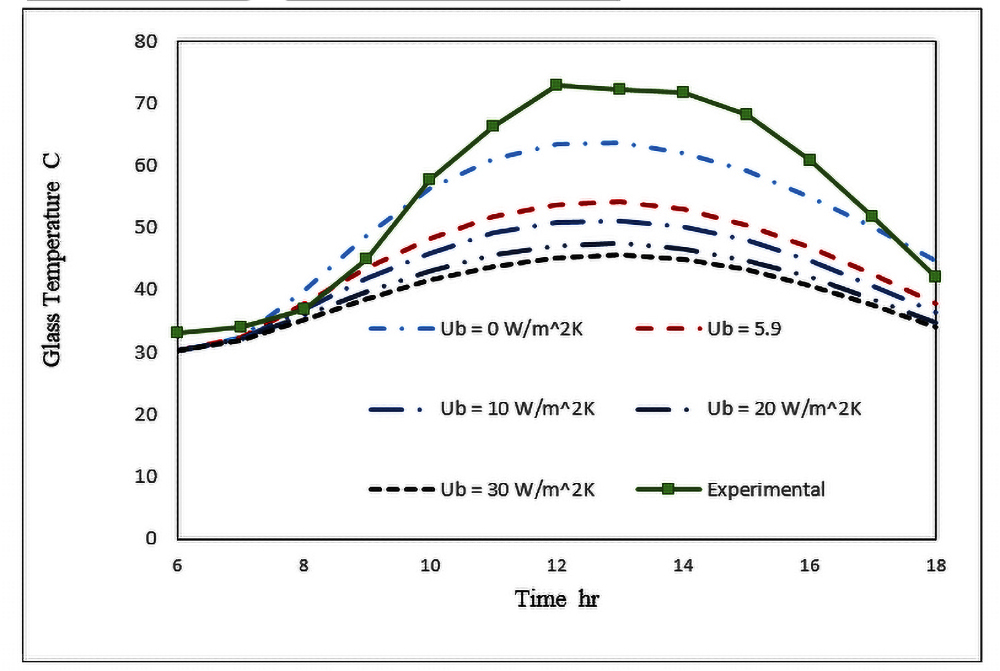
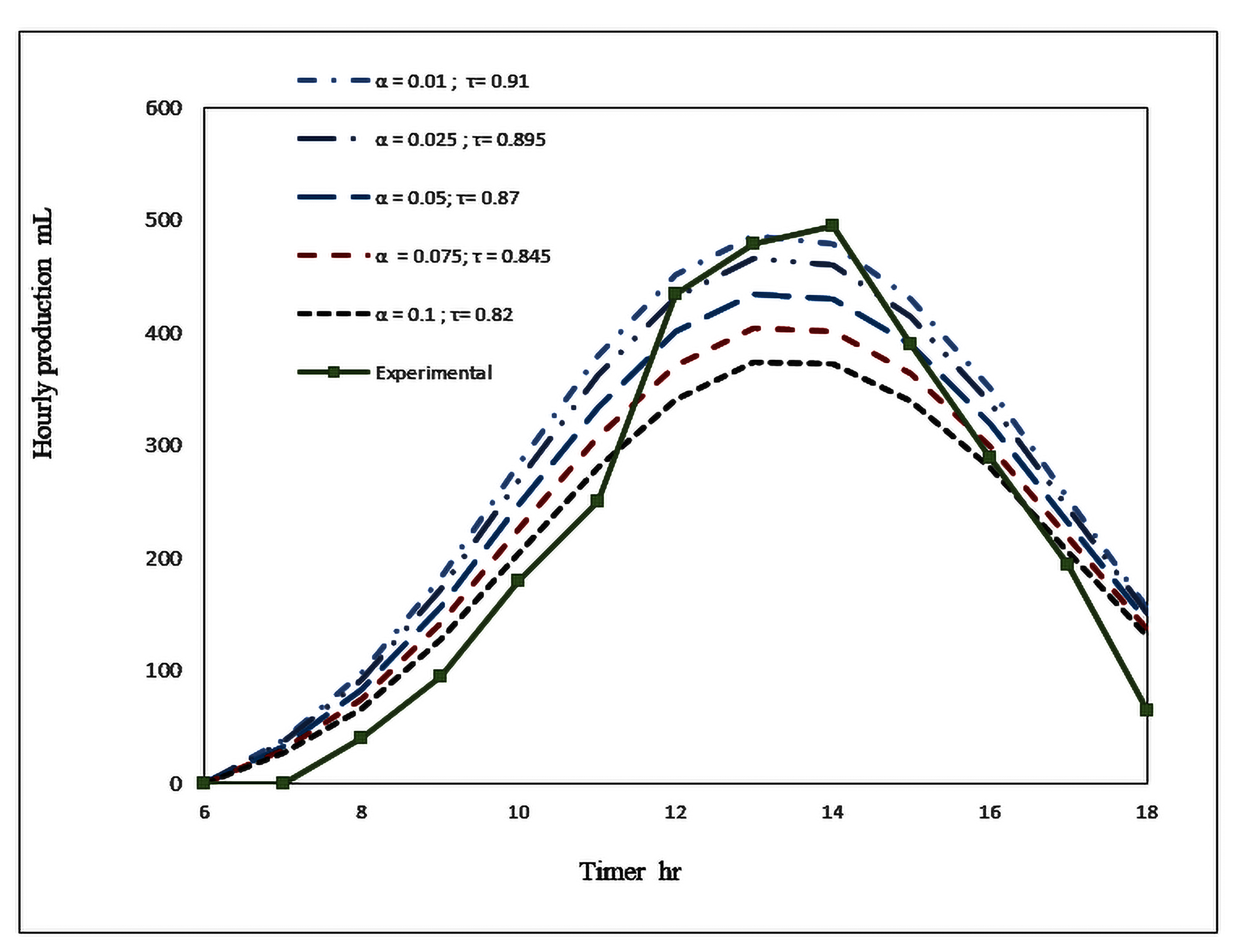
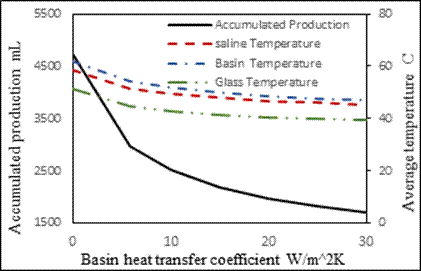
In this research, the effect of the three design parameters on performance of the conventional solar still has been theoretically investigated. These design parameters are basin heat transfer coefficient, glass absorptivity and glass transmiss [5]. To perform the comparison, the model was solved under similar condition as the one used in the experimental study. Other parameters used in this model are shown in table 1. From the current theoretical model the hourly rate production, the accumulated rate production, and the saline water, basin and glass temperatures are calculated and compared with the experimental results (Fig. 2–Fig. 8). This is done iteratively to find the applicable values of basin heat transfer coefficient, glass absorptivity and glass transmissivity. The analysis showed that (see Fig. 2) the experimental and theoretical accumulated production rate are in very good agreement at Ub = 5.9W/m2 K,αg=0.075 and τg=0.845 except around 11:00 a.m. where it shows a discrepancy of 30%. Whereas the hourly production shows a good agreement with a maximum discrepancy of 23%.. At the same conditions, the temperature deviation between theoretical and experiment is by 9.086% for saline water temperature 14.44% for basin temperature and 18.48 % for the glass temperature. As an essential part of the current work, the effect of the three design parameters on the solar still performance is studied. During a design process, a theoretical model that predicts the solar still performance accurately plays a vital role. Thus, knowing the accurate values of these design parameters
in advance will result in a better solar still design. Figures 2-6 shows the effect of the basin heat transfer coefficient on the production and saline water, basin and glass temperatures. Ideally, a solar still must be perfectly insulated and so Ub = 0, which produces the highest accumulated production. An actual solar will always have some basin heat loss depending on the insulation material and installation. Compared with ideal insulated solar still, a Ub of 5.9,10,20 and 30 W/m2K, the accumulated production drops by 37.17%, 47.02 %, 58.53 and 64.02% respectively. The slope of the drop in production is steeper at low Ub (Figure 9) at which the system must be designed. For example if the Ub=1 W/m2K, the drop will 10.64% which is significantly large. Similarly, the effect of U_b’s on the saline water, basin and glass temperatures is significantly large at low Ub’s. The temperatures drops with increasing Ub’s (see Figures 4-5). Based on average values, the deviation from the perfect insulated solar still for Ub of 5.9,10,20 and 30 W/m2K for the saline water is 14.51 %, 18.015% and 24.94% respectively whereas for the basin the drop in temperature is 9.982%, 14.0% 19.32%, and 22.18% and for the glass temperature is 25.77%, 28.88%, 32.75% and 34.71% respectively.
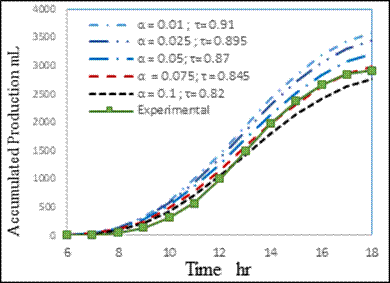
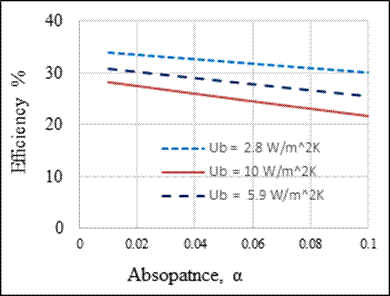
The effect of the glass absorptivity and transmissivity is also studied. The glass reflectance was taken as 0.08 for glass thickness up to 5 mm [22]. Therefore the trade off is then between the absorptivity and transmissivity so the sum of the three is always one. From Figures 7 and 8, the effect of these parameters is obvious. By reducing the glass absorptivity (i.e. increasing the glass transmissivity), the production rate increases due to the fact more solar radiation are passing to the basin. It is essential to use a glass with a low absorptivity in solar still to have high performance. At the same time, it is of great importance to incorporate in the theoretical model accurate values for these parameters in order to produce trustful results. This can be seen from the significant drop in the accumulated production for the absorptivity range of 0.01-0.1 (calculated based on the production at 0.01absorptivity). This drop in accumulated production for absorptivity of 0.025, 0.05, 0.075, and 0.1 is 4.0.%, 10.63 %, 17.04 and 23.28% respectively.
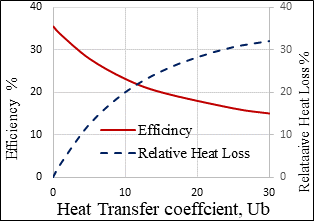
The effect of the basin heat transfer coefficient, Ub and glass absorptivity, α on the solar still efficiency are presented in Figures 10 and 11. As can be seen form Figure 10, the efficiency decreases linearly with increasing the glass cover absorptivity, α. On the other hand, the drop in the solar still efficiency (Figure 11) is more profound when the heat transfer coefficient Ub increases. Figure 11 shows that the efficiency decreases nonlinearly with increasing Ub , where it is steeper at low Ub . The average percentage of the heat loss through the basin is calculated relative the average radiation intensity. These averages are calculated over the 12 hours (6:00 -18:00) during which the system is operating. Figure 11 shows the nonlinear increase in the relative heat loss as expected. The effect of the basin heat transfer coefficient, Ub and glass absorptivity, α are highly significant.
Table 1 applied parameters
| Parameter | Symbol | water | Basin | Glass cover |
| Absorptivity |
|
0.05 | 0.90 | 0.01–0.1 |
| Transmissivity |
|
0.90 | - | 0.91–0.82 |
| Emissivity |
|
0.96 | - | 0.98 |
| Reflectance |
|
0.05 | 0.1 | 0.08 |
|
Specific heat
|
|
4187 | 490 | 670 |
4. CONCLUSIONS
Generally to develop a mathematical model it is required to know the basic design parameters such as the four basic properties that affect radiant energy transfer: transmittance, reflectance, absorptance, and emittance as well as all the external parameters such as the insulation characteristic, which dominate the overall heat transfer coefficient. Previous research using mathematical modeling either gave the values of these provided no clue of what values they used to obtain their results. This study is an attempt to predict production rate of the conventional solar still. In this research, the effect of the three design parameters (Ub , αg and τg) on the performance of the solar still has been theoretically investigated and compared to the experimental results. Iteration was necessary to obtain the values of the design parameters that produce good matching with the experimental which Ub = 5.W/m2 K, αg= 0.075 and τg = 0.845. The effect of Ub found to be significantly large especially at low Ub . Compared to ideally perfectly insulated solar still, i.e. increasing Ub up 30 W/m2 K, the accumulated production drops by 64.02% respectively. Similarly the effect of Ub on the temperatures is significantly large at low Ub. Based on average values, the deviation from the perfect insulated solar still e.g. increasing Ub up to 30 W/m2K for the saline water is 24.94% whereas for the basin the drop in temperature is 22.18% and for the glass temperature is 34.71% respectively. The effect of the αg and τg is also studied. By reducing αg (i.e. increasing τg) the production rate increases due to the fact that more solar radiation are passing to the basin. It is essential to have a glass cover with low absorptivity in solar still to have high performance. The larger the absorptivity, the more significant the drop in the accumulated production. This drop for absorptivity of 0.025, 0.05, 0.075, and 0.1 is 4.0%, 10.63 %, 17.04 and 23.28% respectively. Also the effect of the basin heat transfer coefficient, Ub and glass absorptivity, α on the solar still efficiency was found to be highly significant. The relative heat loss is another measure to show influence of Ub on the system production. In other words, the larger RHL, the less energy consumed by the saline water to evaporator.
Nomenclature

References
[1] Ahmed H M, Ibrahim A G “Performance evaluation of a conventional solar still with different types and layouts of wick materials”, J Energy Technologies and Policy, 6, pp 5-14, (2016).
[2] Alkaisi, A., Mossad, R., and Sharifian-Barforoush, A. “A Review of the Water Desalination Systems Integrated with Renewable Energy” Energy Procedia, Vol 110, pp 268-274, 2017. View Article
[3] Ahmed, H.M., Alshutal, F.S., and Ibrahim, G "Impact of Different Configurations on Solar Still Productivity", Journal of Advanced Science and Engineering Research Vol. 3, No 2, 118-126, 2014
[4] Omara Z.M., Abdullahb, A. S., Kabeelc, A. K., Essaa F. A. “The cooling techniques of the solar stills' glass covers-A review” Renewable and Sustainable Energy Reviews 78. pp 176–193, 2017. View Article
[5] Ibrahim A G, and Ahmed H M, “A theoretical Analysis of a Conventional Solar Still with Different Types of Wick Materials” Unpublished research
[6] Sarray, Y., Hidouri, N., Mchirgui, A., A. B., Brahim “Study of heat and mass transfer phenomena and entropy rate of humid air inside a passive solar still”. Desalination 409, pp 80–95, 2017. View Article
[7] A.F. Muftah,M.A. Alghoul, A. Fudholi,M.M. Abdulmajeed, K. Sopian, Factors affecting basin type solar still productivity: a detailed review, Renew. Sust. Energ. Rev. 32, pp 430–447, 2014. View Article
[8] K.R. Ranjan, S.C. Kaushik, N.L. Panwar, Energy and exergy analysis of passive solar distillation systems, Int. J. Low Carbon Technol. 1–11, 2013. View Article
[9] Abd Elkader M, Safwat Nafy A, Abd Elmotalip A, Mabrouk A. A, “Experimental Evaluation of Solar Still Mathematical Models”, Fourth International Water Technology Conference IWTC 99, Alexandria, Egypt, 2008.
[10] El-Agouz S.A., El-Samadony, Y.A.F., and Kabeelm A.E. “Performance evaluation of a continuous flow inclined solar still desalination system“, Energy Conversion and Management 101, pp 606–615, 2015. View Article
[11] G. P. Mitalas G P, and Stephenso G D, 1962, “Absorption and Transmission of Thermal Radiation by Single and Double Glazed Windows”, National research Council Canada, the Division of Building Research, Research Paper No. 173
[12] Bakari R, Minja R J A,1 and.Njau K N, “Effect of Glass Thickness on Performance of Flat Plate Solar Collectors for Fruits Drying” Journal of Energy, V 2014, Article ID 247287. View Article
[13] Kumar P. V., Kumar A., Prakash O., Kaviti A. K., “Solar stills system design: A review”, Renewable and Sustainable Energy Reviews 51, pp 153–181, 2015. View Article
[14] Ahmed H.M., Hamza R. M, Ibrahim G., and Mahmood Z., " Temperature Analysis of Conventional Solar Still linked to Passive Cylindrical Condensers" Journal of Advanced Science and Engineering Research Vol. 3, No 3, pp 243-251, 2013.
[15] Kumar A., Esakkimuthu, G., Murugave K. K.,” Performance enhancement of a single basin single slope solar still using agitation effect and external condenser” Desalination 399, pp 198–202, 2016. View Article
[16] Alaudeen A, Johnson K, Ganasundar P, Abuthahir A S, Srithar K, “Study on stepped type basin in solar still”, J KSU Engineering sciences, 26, 176-183, 2014. View Article
[17] Ahmed H M, Ibrahim A G, “Performance evaluation of a conventional solar still with different types and layouts of wick materials”, J Energy Technologies and Policy, 6, pp 5-14, 2016
[18] The following Salem Algarni Darin Nutter, PhD, PE, Survey of Sky Effective Temperature Models Applicable to Building Envelope Radiant Heat Transfer, AT-15-029, Conference. Proceeding by ASHRAE, 2015
[19] Haruna, I U, Yerima M, Pukuma A D, Sambo II, “Experimental investigation of the performance of basin type single-slope solar still”, I J Science and technology, 3, pp 169-174, 2014.
[20] Jamil B, Akhtar N,(2014) “Desalination of Brackish Water using Solar Stills-A Review”, Proceedings of the International Conference on Environment and Energy (ICEE-2014), 201
[21] Madhlopa A, Clarke J A,“ Computation of irradiance in a solar still by using a refined algorithm”, Renewbale energy, 51, pp 13-21, 2013. View Article
[22] Gurdian SunGuard Advanced Architectural Glass. View Article Or www.SunGuardGlass.com

