Journal of Fluid Flow, Heat and Mass Transfer (JFFHMT)

ISSN: 2368-6111

1. Introduction

Water is one of the most essential elements for life on earth. Two thirds of the earth’s surface is covered by water. However, only 2.5% of this vast quantity is fresh water, and less than 1% is readily accessible to humans [1]. The human body consists of approximately 75% water and human life strongly relies on drinking water that is necessary for the human body to function properly [2]. Even though, the knowledge base is inadequate to determine an optimal fluid intake because of the myriad of factors that are involved [3], some health officials recommend drinking at least eight glasses (approximately two litres) of water daily to reduce the risk of diseases including some types of cancers. Many illnesses affecting millions of people worldwide, even in developed countries, stem from a simple and mostly unrecognized cause, the insufficient daily ingestion of water [4]. Unfortunately, numerous factors such as climate change and poor resource management lead to water shortages in both the developing and developed countries. Based on recent data published by UNICEF and the World Health Organization (WHO), around 663 million people lack access to adequate drinking water [5]. The United Nations claim that every 8 seconds, one child under age 16 dies because of illnesses related to drinking of contaminated or dirty water.

The industrial sector uses about 20% of global freshwater withdrawals (for hydro and nuclear power generation, industrial processes and thermal power generation), it is forecasted that the water volume used by industry will rise from 752 km³ per year (1995) to 1170 km³ per year in 2025. This amount corresponds to 24% of total freshwater withdrawals [6].

There exist numerous sources of fresh water: rivers, lakes, underground aquifers, rain, and moisture contained in the atmosphere. The global atmosphere contains a huge amount of water vapour which, in addition to render the fresh water supply renewable in many parts of the world, constitutes a potential source of water for drinking purposes. Indeed, it is estimated that 10 000 to 30 000 m³ of water is available in one square kilometre of atmospheric air in most regions [7]. Collecting water from atmospheric air is therefore considered as a supplemental method to alleviate the shortage of drinking water. Even though it is relatively small, it is nevertheless a viable water resource because it occurs naturally in most locations around the world [8]. The extraction of water from atmospheric air can be done using three different methods: condensation [9]-[10], absorption [11], and adsorption [12]-[14]. For the condensation-type method, moist air passes over a cooling surface that is maintained at a temperature that is below the air dew point [15]. Small systems are sold commercially to produce between 10-50 litres per day of fresh water from air: Watermill (Element Four, Kelowna, Canada), Airwater Hellas (Thessaloniki, Greece), Air2Water Dolphin T16 (Santa Monica, USA), etc. Currently, the use of dew water for agricultural irrigation is limited even though many water collection systems were evaluated with some success for their effective dew harvesting capabilities. Tomaszkiewicz et al. [16] showed that with a condensing area of 2 m², one can harvest sufficient water to irrigate a tree seedling for a period of 30-40 days corresponding typically to 4.5 L/seedling, which would be beneficial for reforestation in arid and semiarid regions. To foster the development of this technology, it is paramount to evaluate the impact of many variables affecting dew harvesting [8].

It is obviously interesting to harvest small quantities of water from moist air without resorting to external energy supplies. Some beetles living in the desert use this principle to collect water for their drinking needs [17]-[18]. Dew forms when a surface cools below the dew point temperature of the surrounding air, which occurs mostly on cool nights with clear sky and light winds when radiative cooling is the dominant mechanism of heat loss [19]. These passive water collection methods from the atmospheric air, also referred to as dew collectors, have been investigated by many researchers [20]-]25].

The main advantages of these methods are the negligible labour and energy requirements. Kogan and Trahtman [26] have examined the possibility of recovering water from dew in arid regions. They modified the traditional model of the Crimean water collector by re-examining the role of the air draught in the condensation process. Beysens et al. [27] have critically assessed the work of Kogan and Trahtman [26] and stated that their assumptions were incorrect and the passive dew collector as proposed could not generate as much water as it was claimed. In order to increase the dew condensation from atmospheric air, Muselli et al. [28] constructed and installed two large inclined insulated plane radiative condensers in Corsica Island, France. The performance of the two passive collectors was compared with a horizontal plane, used as a reference. They observed an increase in dew collection with the inclined planes. Clus et al. [29] evaluated dew formation on inclined plane collectors in water-scarce low islands and concluded that dew harvesting appears as an attractive option as a complementary water source. In another study, Clus et al. [30] compared different radiation-cooled dew collectors using Computational Fluid Dynamics (CFD) numerical simulations. Funnel shape collector was compared with 30° inclined planar condenser as a reference, and the best performance was found for a funnel shape with cone half-angle of 60°. Their simulation did not account for the condensation process. Yan and Xu [31] evaluated four different types of dew collectors and found that poplar wood stick collector was optimal. Kidron [32] evaluated the dew condensation on smooth and ragged Plexiglas, bright limestone and dark flint cobbles in order to establish their relationship with the dew yield. Smooth Plexiglas surface gave higher yield than the ragged Plexiglas. No significant differences were found with the limestone and the flint cobbles. Additionally, their study accounts for the effect of neighbouring bodies encountered naturally in the environment such as cliffs, caves, shrubs, and cobbles.

Atmospheric pollutants such as solid particulates, contaminants, microorganism, and heavy metals can accumulate over dew condensing surfaces and can affect the quality of water, especially if it is destined for human consumption. Acker et al. [33] measured nitrite in atmospheric dew samples to assess the quality of water recovered from dew. The samples were collected at different German mountain sites and at a site south of the Bordeaux urban area (France). Often, significant amounts of nitrite have been observed. Muselli et al. [34] investigated the relative contributions of dew and rain water in the Mediterranean Dalmatian coast and islands of Croatia during the dry summer season and they concluded the usefulness of employing inclined dew condensers for that season. Lekouch et al. [35] measured pH and electrical conductivity and analyzed the chemical properties of water collected from dew and rain. The pH of dew and rain was practically the same with very weak acidic properties. Based on their results, the collected dew and rain water corresponded to the WHO requirements for drinking water [36], except for Mg²⁺ for which the concentration was higher than the recommended value. In a separate study, Lekouch et al. [37] collected water from dew during a one-year period in the dry land area of Mirleft (Morocco) and showed that the quantity of collected water was about 40% of the rain accumulated over the same time period. Beysens et al. [38] evaluated the physico-chemical and biological properties of dew and rain water during one year in Bordeaux, France. They found that the presence of chemicals in harvested water was below the limits directed by the WHO whereas the biological limit was sometimes exceeded. Odeh et al. [39] performed a similar study in Amman (Jordan) to evaluate the presence of particulates in dew water from urban dew collectors. They found that the quality of water was adequate for agriculture use whereas for human consumption, an inexpensive pre-treatment would be required to remove dust coming mainly from the neighbouring desert.

Several parameters have an impact on the ability of passive dew collectors to yield appreciable amounts of water. The main parameters that could impact water collection are the air temperature, the relative humidity, the wind speed and direction, the opacity of the sky to earth radiation and the properties of the collecting plate. Passive collectors compared to active collectors must operate in a narrower time window corresponding to the night time period in which the collector plate can lose energy by radiative cooling. During that period of radiative cooling, the plate temperature is dependent on the effective sky temperature. The sky temperature under clear night sky can be estimated as a function of air and dew point temperatures. Water collection will occur when the plate temperature reaches a temperature that is at, or below, the dew point.

Maestre-Valero et al. [40] presented a model where an energy balance was performed to predict the water yield and temperature of the dew condenser. Their model showed the sensitivity of the dew yields to changes in relative humidity and downward longwave radiation. The model was validated in south-eastern Spain and could be a useful tool for predicting the dew yield in arid regions. Beysens [41] developed a model based on cloud coverage, wind velocity, air and dew point temperature data collected at least once daily. The latter model does not consider precise radiative and heat transfer data. Their experimental results demonstrated that the dew yield was mainly limited by convective losses. Benlattar et al. [42] proposed a model that includes meteorological parameters and thermal balance, and fitted this model to predict the dew mass evolution. They showed that the relative humidity, the wind speed and cloud cover affect the dew collection. Lekouch et al. [43] used an artificial neural network (ANN) to model the dew condensing process on the rooftop of buildings using meteorological data. Their model could be used to predict dew formation at 15 other major cities in Morocco. Sharan et al. [44] described the construction and functioning of a combined rain and dew harvesting plant for drinking water. The design and evaluation were performed via CFD simulation, and the dew yield was calculated using meteorological data. Their economic evaluation suggested that water obtained with this method could be cheaper or similar to water obtained by reverse osmosis.

In the present investigation, a parametric study is performed using commercial CFD software to determine the collection plate temperature and the rate of moisture condensation over a wide range of atmospheric conditions. The system consists of a horizontal plate over which flows a stream of air, at a given temperature and relative humidity. This study is aimed at investigating the effects of air temperature, relative humidity, wind velocity and plate emissivity. In addition, the performance in terms of the rate of water condensation of a flat plate dew condenser was compared with that of triangularly corrugated plates with different base and height aspect ratios and V-shape dew condensers. The problem is first defined by providing the main mechanisms and equations involved in passive dew condensation and followed by a presentation of the results where the effects of the wind speed, air temperature and relative humidity, plate emissivity and plate geometry are presented.

2. Problem Statement

Figure 1 shows a horizontal flat plate exposed to the sky, which is employed for passive water extraction from moist atmospheric air. The plate, which has an arbitrary dimensions of 1-m long and 1-m wide, is assumed to be perfectly insulated from underneath such that it exchanges heat only through the top surface exposed to the sky. It is assumed that the plate is very thin and has a low thermal conductivity such that there is an infinite resistance to conduction heat transfer along the plate. Consequently, the local plate temperature can be predicted from the energy balance of the different modes of heat transfer, which in this case are radiation, convection and condensation. The plate loses energy by radiative heat transfer to the clear night sky (q_rad.) and gains energy by convective heat transfer between the plate and air (q_conv.). In addition, if the temperature anywhere on the plate drops below the dew point temperature of ambient air, the plate also gains energy from the condensation of water vapour from air on the plate (q_conden.). It is assumed that whenever condensation occurs, the condensate is instantaneously removed from the surface so that the surface properties are not affected by condensation.

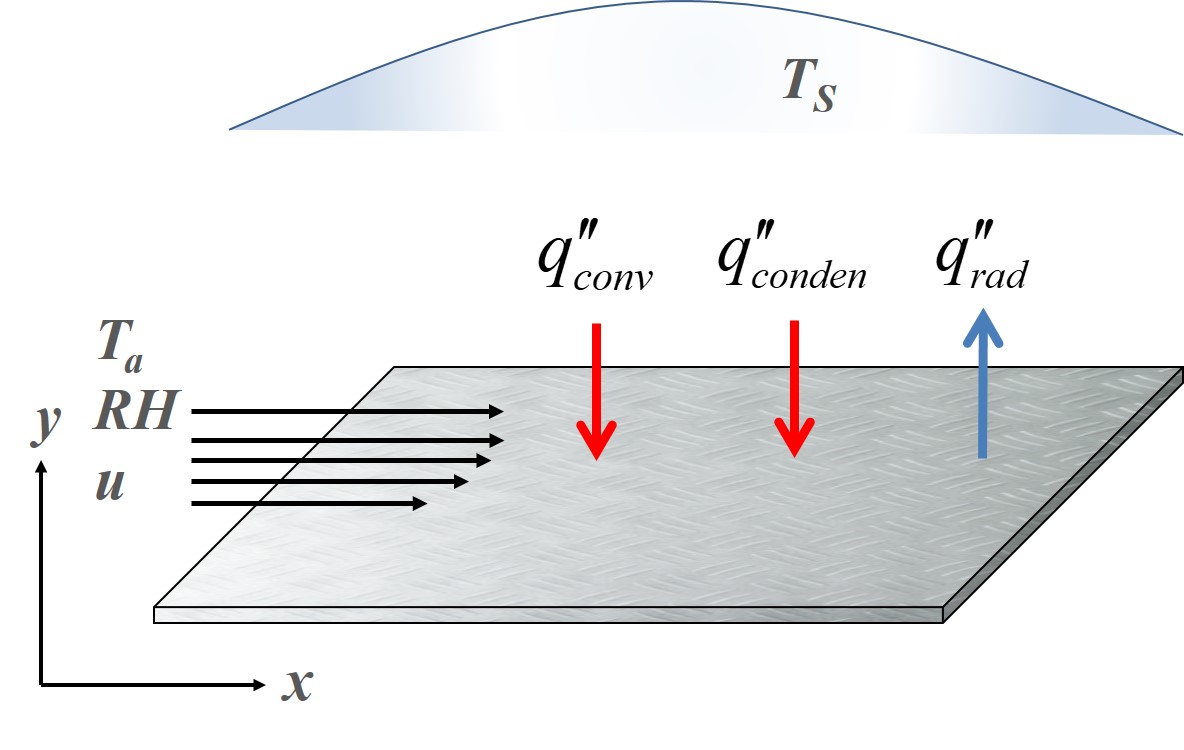
The local energy balance on the plate (T_a > T_p) is given by:

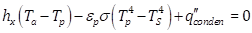
where T_p, T_s, and T_a are the local plate, effective sky, and ambient absolute temperatures, respectively. In addition, e_p, s, and h_x are the plate emissivity, the Stephan-Boltzmann constant, and the local heat transfer coefficient, respectively.

To determine the plate temperature, the heat flux due to condensation should be expressed in terms of T_p. However, condensation of the water vapour on the plate is driven by the difference between the specific humidity of air (H) and the specific humidity at the plate surface (H_w):

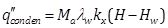
where k_x is the local mass transfer coefficient for the transport of the water vapour across the boundary layer and λ_w is the latent heat of vaporization or condensation. On the other hand, the driving force for condensation can be expressed in terms T_p using the following equation [45]:

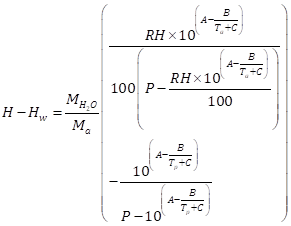
where the A, B, and C are the constants of Antoine equation for water. They are equal to 7.2324, 1750.285^oC and 235.0^oC, respectively [46]. P is the pressure in [kPa], RH is the relative humidity of air in the free stream, and M the molecular weights of air and water. Eq. (3) is defined with all temperatures expressed in [^oC].

The latent heat of condensation at a dew point temperature T_d expressed in [^oC], which corresponds to the given relative humidity of ambient air, can be evaluated from the following equation, which was obtained by fitting the data from steam tables:

                                                                                                             

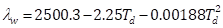
It is important to emphasize that if T_p < T_d, should also include the sensible heat of water, which is directly proportional to the difference between T_d and T_p, but in practice this sensible heat is negligible compared the latent heat.

For the laminar flow of moist air over a flat plate, the local mass transfer coefficient for the transport of the water vapour from the free stream of air to the plate surface can be evaluated from the following equation [47]:

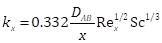
in which the local Reynolds number is given by:

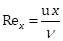
and x is the distance from the leading edge of the plate, u is the wind velocity, n is the kinematic viscosity of air, Sc is the Schmidt number, and D_AB is the diffusivity of water vapour in air. A similar equation is also applicable for the evaluation of the local heat transfer coefficient:

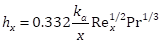
where k_a is the thermal conductivity of air and Pr is the Prandtl number. It is important to emphasize that Eqs. (5-7) are applicable for an isothermal plate, which is not the case in this analysis. However, the application of these equations will help understanding the effect of different parameters on the plate temperature and the condensation rate.

Substitution of Eqs. (3, 5-7) into Eq. (2) and then back into Eq. (1) leads to:

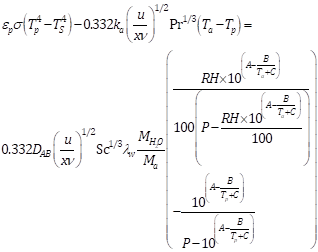
The determination of T_p from Eq. (8) requires the numerical value T_s, which can be estimated from the sky emissivity (e_s) using the following equation [48].

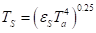
Gliah et al. [49] have shown the significant variability of the estimation of the sky temperature. In turn, the sky emissivity is estimated by the following equation [50]:

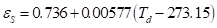
The dew point temperature, which is required by Eq. (10) but also by Eq. (4), is evaluated using the Magnus formula [51] with temperatures T_d and T_a expressed in degrees Kelvin:

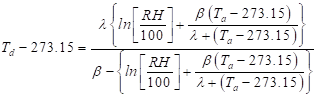
The parameters l and b in Eq. (11) are equal to 243.12^oC and 17.62, respectively.

The objective of this study is to investigate the effect of environmental parameters on the plate temperature and the condensation rate of moisture on the plate. Variables u, T_a, RH, e_p, and plate geometry are examined. Specifying the above parameters allows the determination of the local T_p from Eq. (8). Moreover, dividing the right hand side of Eq. (8) by λ_w gives the local condensation flux. The integration of the local condensation flux over the entire plate leads to the total condensation rate.

To facilitate the parametric studies on the effect of the above-mentioned parameters on T_p and the condensation rate, two-dimensional steady state simulations in the present study were carried out using commercial CFD code Fluent®. The commercial code, Fluent®, with a segregated solver was used to simultaneously solve the equations of continuity, momentum, heat and mass transfer. The governing differential equations and boundary conditions were discretized by the finite volume method (FVM). For the pressure-velocity coupling, the well-known SIMPLE (Semi-Implicit Method for Pressure-Linked Equations) algorithm was used. The first-order upwind discretization scheme for convective terms was employed, and the convergence criterion was set to 10^‑6. The parametric study was performed over a wide range of wind speed, relative humidity, ambient air temperature, and plate emissivity. The range of the wind speed considered results in a laminar boundary layer over the entire plate, which was assumed in the derivation of Eq. (8). Due to the higher velocity and temperature gradients at the leading edge of the plate and in its proximity, finer discretization meshes were used in that region.

Results of this parametric study can clarify the role of u, T_a, RH, and e_p on the ability of a surface exposed to a clear night sky to collect water and to assist in the design of passive water collectors having optimal efficiency. The underlying criterion is truly the difference in temperature between the plate temperature and the dew point temperature. The geometry of the passive collector may also have an influence on the ability to collect dew water and will be briefly assessed in this investigation. The evaluation of the condensed moisture at different conditions for a specific geographic area will be the determining factor in deciding on constructing an apparatus for water extraction from atmospheric air for different seasons.

3. Results and Discussion

3. 1. Effect of wind speed

Wind speed plays a key role in convective heat transfer between the plate and ambient air and, consequently, in the condensation rate on the plate when the plate temperature is below the dew point. As indicated by Eq. (8), an increase in the wind speed u increases both the convective heating of the plate and the mass transfer coefficient for condensation. However, the effect of u on the condensation rate on the plate is not immediately obvious, because as u increases, the driving force for condensation decreases, while the mass transfer coefficient for condensation increases.

Figure 2 presents the variation in the plate temperature with the distance from the leading edge for five different wind speeds when the ambient air temperature is 293 K (20^oC) with a plate emissivity of 0.94. Figure 2a presents the plot of the plate temperature for an air relative humidity of 40% while Figures 2b and 2c present the plate temperature profiles for an air relative humidity of 60% and 80%, respectively. All data in Figure 2 were obtained using the commercial CFD code Fluent^®. The dew point temperature evaluated using Eq. (11) was also plotted for comparison. It is important to emphasize that the plate in this study was assumed to be nonconductive so that its temperature changes locally according to the changes in the convective, radiative and condensation components of the energy balance along the plate.

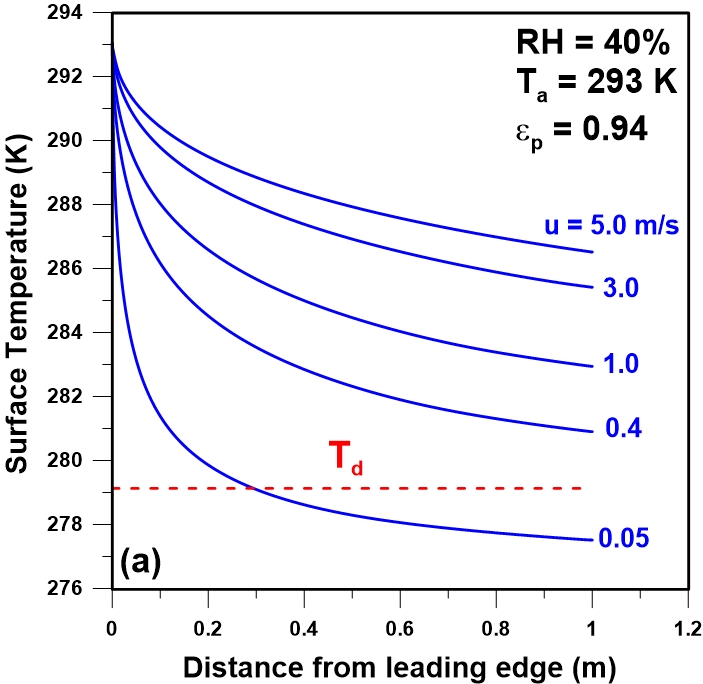
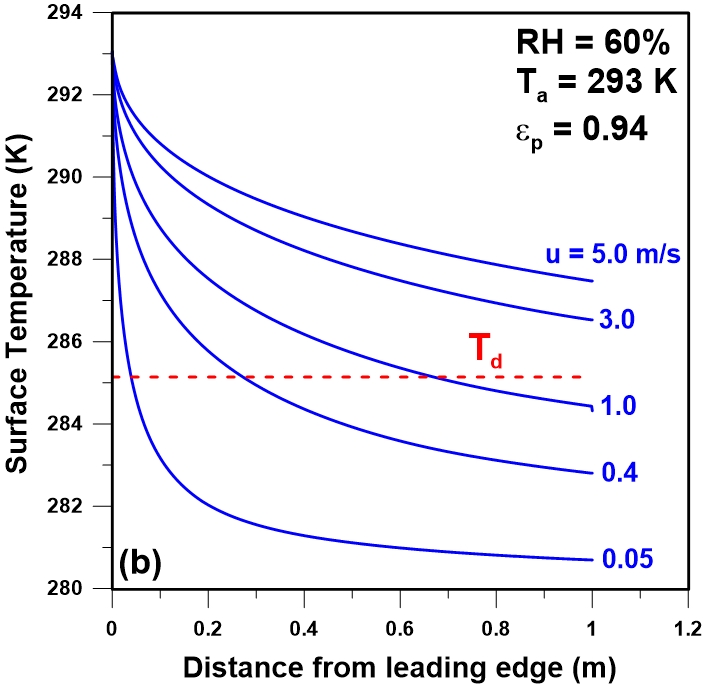
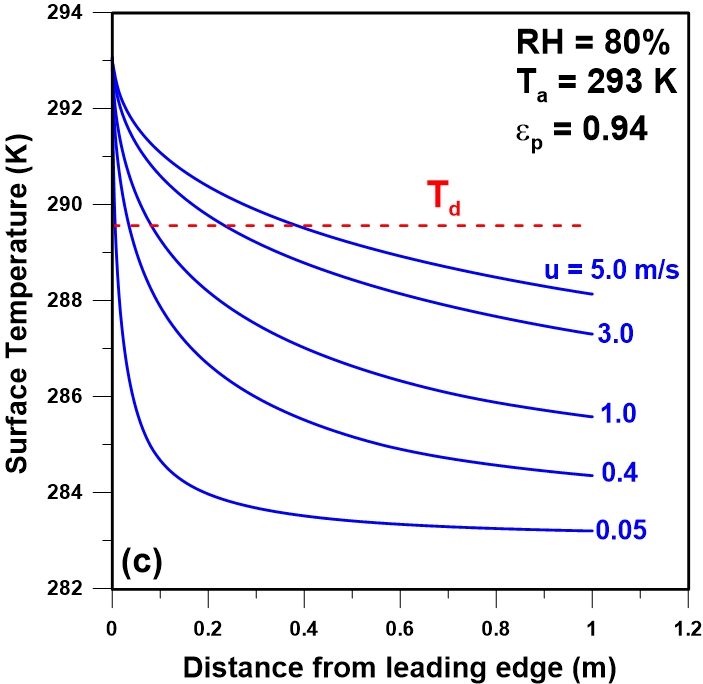
At the leading edge of the plate, because of the thinner boundary layer, the convective heat transfer coefficient is relatively large and the plate temperature remains closer to the air temperature. As the air flow moves downstream, the convective heat transfer coefficient decreases and the plate temperature gradually decreases reaching the lowest value at the end of the plate. It is evident from Figure 2 that at a given distance from the leading edge, regardless of the relative humidity, the plate temperature decreases with a decrease the wind speed, which is expected considering that the convective heat transfer coefficient increases with wind speed. As long as the plate temperature remains above the dew point, the plate is heated only by convection such that the plate temperature results from the balance between the convective heating and the radiative cooling. When the plate temperature (T_p) drops below the dew point temperature (T_d), the plate is also heated by the condensing water vapour, and the rate of heating is proportional to the rate of condensation.

For the lower wind speed (u = 0.05 m/s), the convective heat transfer coefficient is very small which leads to a relatively low plate temperature since the relative contribution of radiation becomes more important. In this case, even though at lower plate temperatures the radiative heat transfer is smaller, the rate of heat transfer by convection decreases more rapidly than the decrease of the rate of heat transfer by radiation. Simulation results for a relative humidity of 40% (Figure 2a) show that the dew point temperature is lower than the plate temperature for all wind speeds considered except for the last portion of the plate at the lowest wind speed. As a result, it would be impossible to recover water under these conditions. Similar plate temperature profiles for a relative humidity of 60% and 80% at the same wind speeds and air temperature are presented in Figures 2b and 2c. In Figure 2b, for a wind speed of 0.05 m/s, nearly the entire length of the plate is lower than the dew point whereas for a wind speed of 1 m/s more than half of the latter portion of the plate temperature is below the dew point. In Figure 2c, because of the higher moisture content and the corresponding higher dew point temperature, it would be possible to recover some water even at a wind speed of 5 m/s.

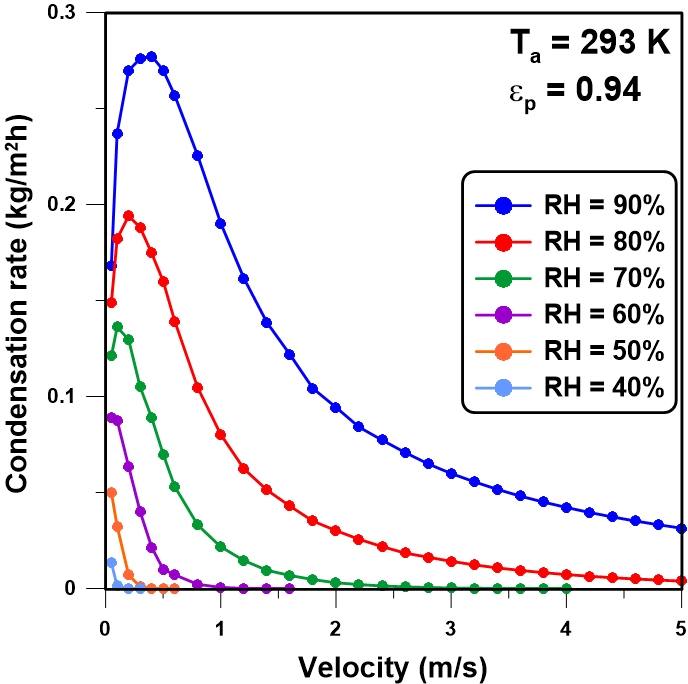
Figure 3 presents the effect of the wind speed on the condensation rate on the plate for an ambient air temperature T_a = 293 K and for different values of the relative humidity. It can be observed that, at lower wind speed and higher relative humidity, the condensation rate under these conditions increases with the wind speed. This effect is not immediately obvious because, as the wind speed increases, the plate temperature increases, which in turn decreases the driving force for condensation. However, this decrease in the driving force is overcompensated by an increase in the mass transfer coefficient for condensation, which leads to a net increase in the condensation rate with the wind speed. It is important to emphasize that a further increase in the wind speed will eventually lead to a maximum condensation rate and then a decrease in the condensation rate because the higher heat transfer coefficient will eventually bring the plate temperature above the dew point temperature. For lower relative humidity, this maximum condensation rate is lower and occurs at a much lower wind speed as was suggested by the results of Figures 2a and 2b where the plate temperature is below the dew point for a larger surface of the plate. increases the forced convection heat transfer and consequently the plate temperature increases. On the other hand, higher air velocity introduces more moisture to the plate by virtue of a higher mass transfer coefficient such that it favours the recovery of more water from ambient air. The condensation rate is based on a compromise between these opposite effects. Similarly for a totally different system, Monteith [52] found that for dew condensation on grass, the condensation rate was negligible for wind speed of less than 0.5 m/s at 2 m from the ground whereas the maximum condensation rate was obtained for wind speed of less than 1.5 m/s.

3. 2. Effect of the relative humidity

Air humidity is related to the amount of water vapour that air contains and uniquely defines the dew point temperature. Therefore, the potential for recovering water from air should increase with the air relative humidity for a given air temperature. On the other hand, in addition to dictating the dew point temperature (Eq. 11), the relative humidity has also an impact on the sky emissivity and the effective sky temperature. As the relative humidity increases, the sky emissivity increases (Eq. 10). In turn, an increase in the sky emissivity results in an increase in the effective sky temperature (Eq. 9). As the effective sky temperature increases, the radiative cooling decreases. It is important to emphasize that the radiative cooling is the only mechanism by which the plate temperature can drop below the dew point of air, which is the necessary condition for the condensation on the plate to occur. Consequently, the effect of the relative humidity on the condensation rate on the plate is not as obvious as it might appear.

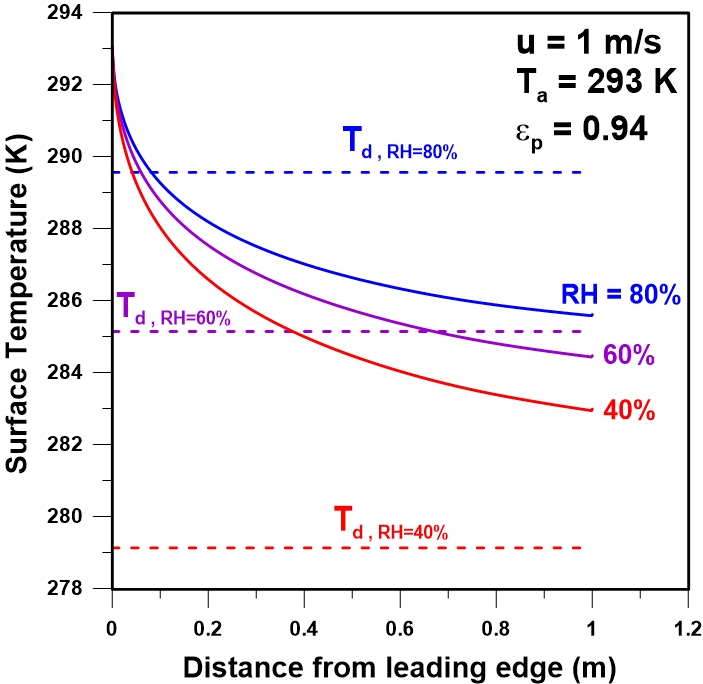
Figure 4 presents the variation of the plate temperature along the plate surface for three different percentages of the air relative humidity when the ambient air temperature is 293 K, the wind speed is 1 m/s and the plate emissivity is 0.94. The corresponding dew point temperatures are plotted for each relative humidity. Results show that water recovery from air would be possible for a relative humidity of 80%. On the other hand, the plate temperature is higher than the dew point temperature for a relative humidity of 40% and 60% such that these conditions are not feasible for water collection at that particular wind speed.

At a given distance from the leading edge, the plate temperature increases with the relative humidity of air because the latter increases the effective sky temperature. In addition, the decrease in plate temperature is more pronounced when the relative humidity is lower, such that the difference of the plate temperature between curves of different relative humidity increases along the plate. This increase occurs because the driving force for condensation increases, which leads to a higher condensation rate and higher heating of the plate with this mode of heat transfer. It is also important to note that, despite the increased heating of the plate by condensation, its temperature continues to decrease. This observed decrease confirms that the plate temperature is primarily controlled by the convective and radiative heat transfer phenomena.

3. 3.   Effect of ambient air temperature

Since the ambient air temperature changes throughout the year and throughout the night, it is interesting to examine how it influences the potential of water recovery using a passive dew collector. For a constant relative humidity, the water content of ambient air increases with air temperature and greater water availability thereby exists at higher temperature. On the other hand, a decrease in air temperature for a constant relative humidity not only leads to a decrease in the plate temperature but also leads to a decrease in the dew point temperature, the sky emissivity and the effective sky temperature such that the exact effect of the air temperature is not trivial.

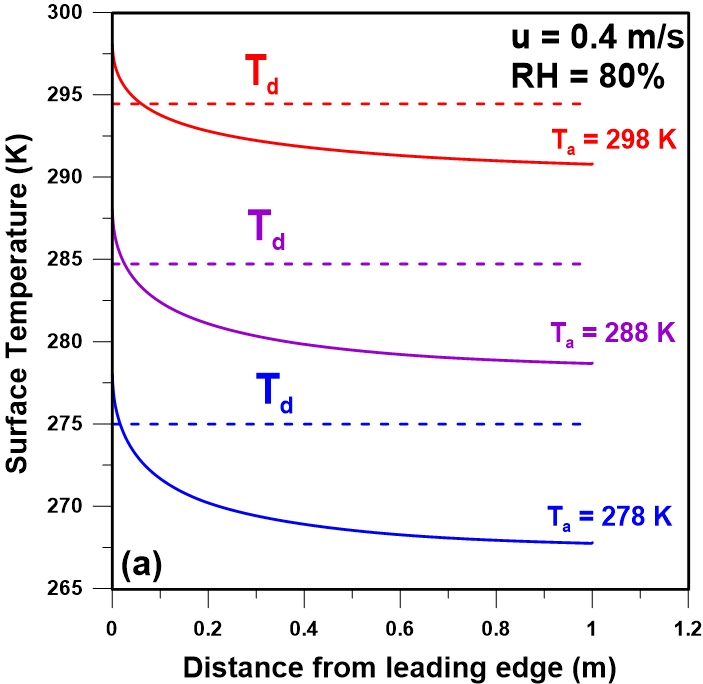
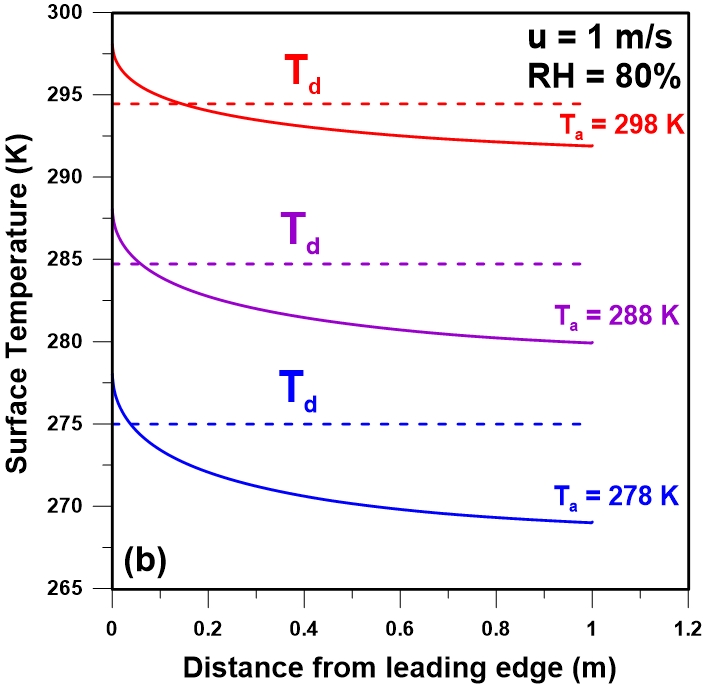
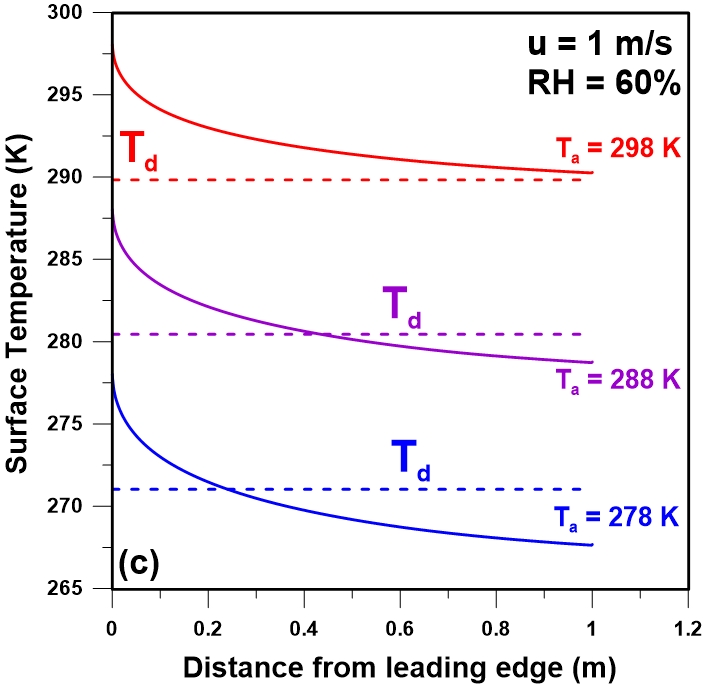
A series of simulations were performed to calculate the plate temperature profiles for six different air temperatures (5-30^oC) and two different wind speeds (0.4 and 1 m/s) for a constant percentage relative humidity of 80%. Results are presented in Figures 5(a-b). The dew point temperature associated to each condition has also been indicated on each plot of the temperature profiles. The effect of the air temperature is significant. In both cases, a decrease in the fraction of the plate that is below the dew point is observed at higher air temperature. This decrease is more pronounced at higher air velocity. Figure 5c shows the effect of the air temperature for a wind speed of 1 m/s and a constant relative humidity of 60%. Results show that the plate temperature at some locations on the plate is higher than the respective dew point. For example, for an air temperature of 298 K and u = 1 m/s, the plate temperature is above the dew point over the entire length of the plate.

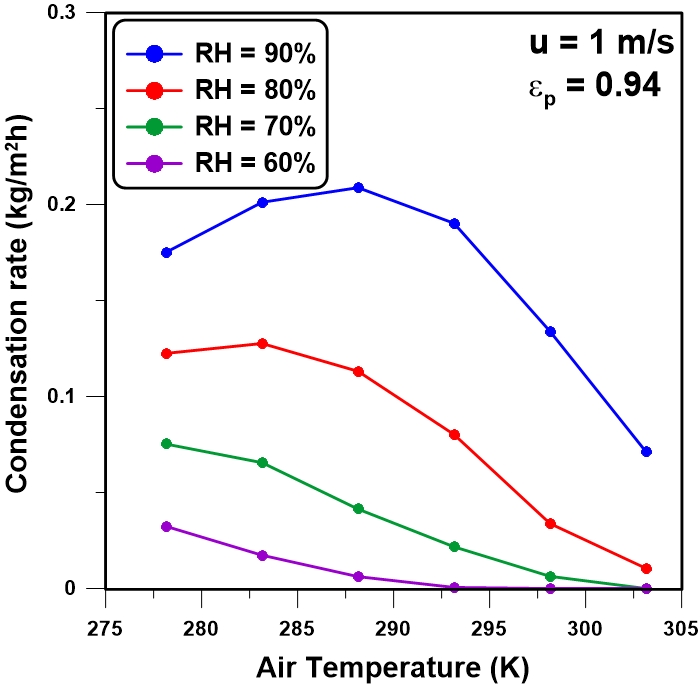
The effect of the ambient temperature on the condensation rate for four levels of the relative humidity is presented in Figure 6. Results show that a maximum in the condensation rate occurs at higher relative humidity. Indeed, the condensation rate increases initially when the ambient temperature increases, and then goes through a maximum condensation rate prior to decrease with an increase in ambient temperature. At a constant relative humidity, the amount of water present in air is higher at higher ambient temperature. However, higher moisture content inhibits radiation losses to the sky such that the plate temperature remains closer to ambient temperature. Competition between these effects results in specific plate temperature distribution and water collection rate. At higher ambient temperature and lower relative humidity, the plate temperature is higher than the corresponding dew point temperature over a portion of the plate, which leads to a lower water collection rate. At an ambient temperature lower than the ambient temperature at which the observed maximum condensation rate occurs, the plate temperature becomes cooler but, since the air water content is significantly lower, the water condensation rate is lower.

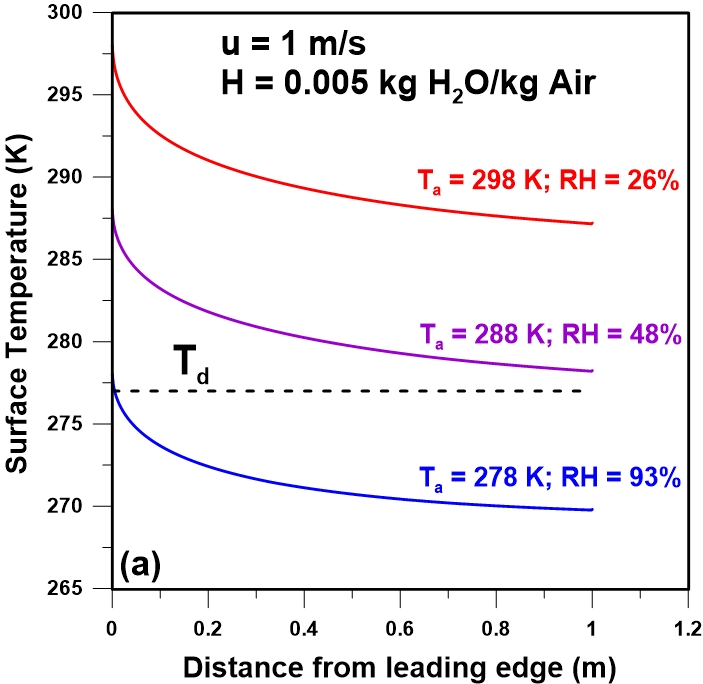
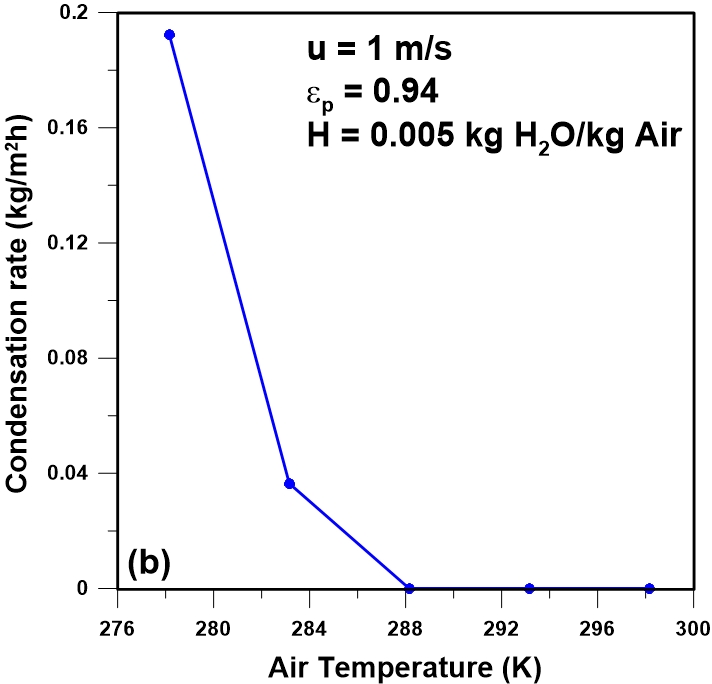
In practice, when the air temperature changes, the air moisture content may remain more or less constant until the dew point temperature is reached. As a result, a decrease in temperature is accompanied by an increase in the relative humidity. To test the effect of the air temperature on the rate of condensation for constant moisture content, a series of simulations were performed at five different air temperatures. Results are presented on Figure 7(a-b) for fixed moisture content of 0.005 kg H₂O/kg dry air. Because the air moisture content is constant for all air temperatures, the dew point temperature remains constant at approximately 277 K. At an air temperature of 278 K, the plate temperature over nearly the total plate surface area is below the dew point temperature and condensation will occur over a large portion of the plate area. An increase in the ambient temperature leads to a higher plate temperature under steady state conditions. Based on the results of Figure 7a, as the air temperature is increased, the plate temperature also increases and condensation prevails over a much smaller fraction of the plate. For an air temperature in the vicinity of 288 K, the temperature of the entire plate remains higher than the dew point temperature and no condensation occurs (Figure 7b).

3. 4.   Effect of the plate emissivity

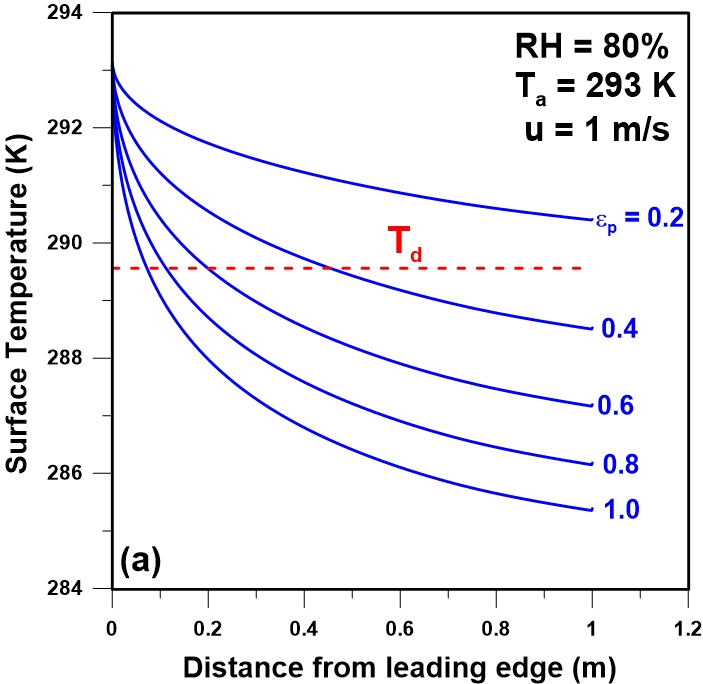
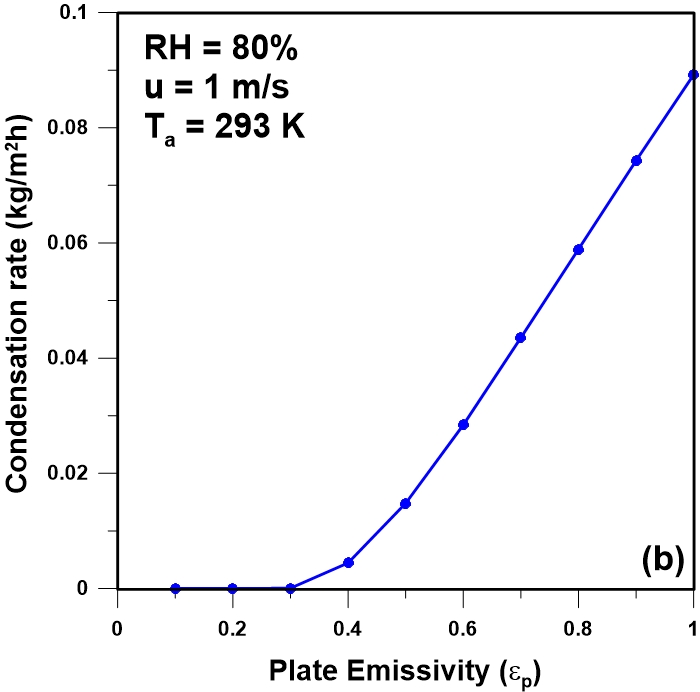
Emissivity is defined as the percentage of the energy a plate would radiate compared to a perfect blackbody at a given temperature. The plate emissivity should therefore affect the plate temperature and the rate of water condensation. Figure 8a presents the results of the variation in the plate temperature as a function of the distance from the leading edge of the plate for five different values of the plate emissivity and for an ambient temperature of 293 K and a relative humidity of 80%. As expected, results show that the plate temperature increases as the plate emissivity decreases, resulting in a higher water vapour partial pressure of the condensing water at the surface of the plate and a lower driving force for mass transfer. The higher water vapour partial pressure translates in a decrease in the water condensation rate at the surface of the plate as shown in Figure 8b. Results show that the rate of condensation is nearly a linear function of the plate emissivity. It is therefore important to have a plate emissivity as high as possible to favour water collection with passive dew collectors.

3. 5. Effect of the geometry of the dew collector

To improve the performance of passive water collectors, their geometry can be adapted to maximize the water harvesting rate. In this investigation, the performance of triangularly-corrugated surfaces with different base and height of corrugations and V-shape collectors with an angle of 120^o was also studied and compared with the flat plate collector to determine the impact of the collector geometry. Figure 9 shows the geometrical configuration of triangularly-corrugated and V-shape passive condensers. The impact of the radiation view factors is considered in the calculation of the radiative heat transfer for both configurations.

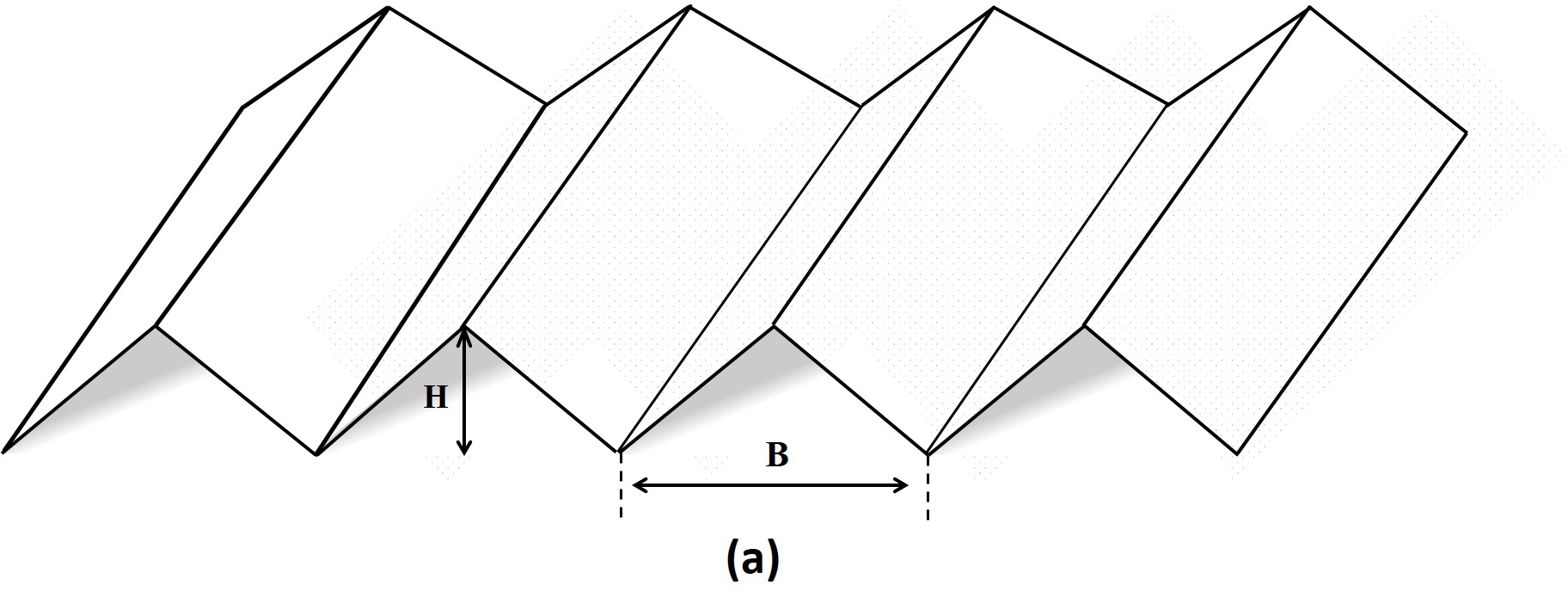
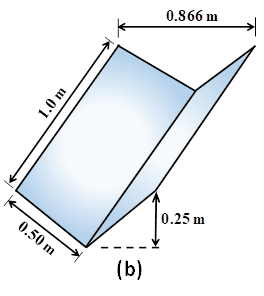
Figure 10(a-b) shows the water condensation rate as a function of the wind speed for various configurations of the triangularly-corrugated collectors. Results show that the rate of condensation for a corrugated plate is greater than for horizontal flat plate condensers at lower wind speeds. At higher wind speeds, the effect the geometrical effect of the plate on the condensation rate becomes negligible and the flat plate may in fact performed better. Based on the results obtained at lower wind speeds, it is clear that by decreasing the base and increasing the height of the triangular channels, the condensation rate increases.

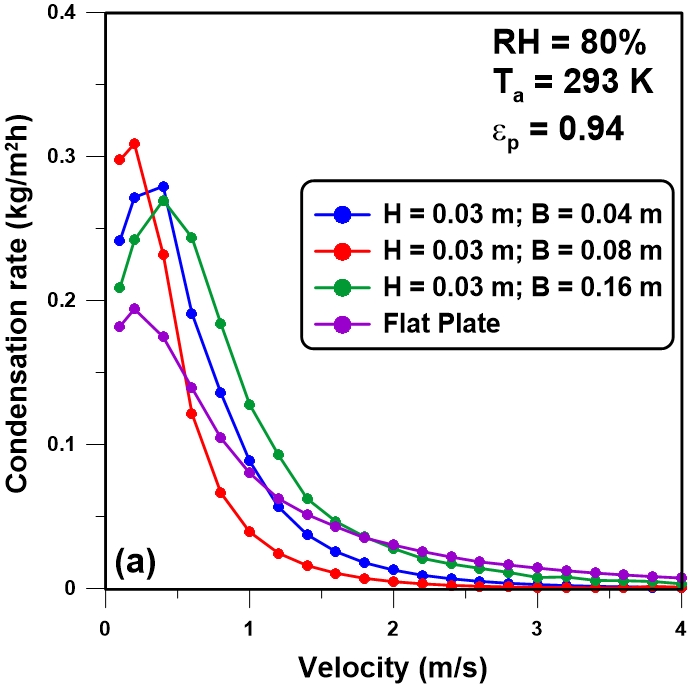
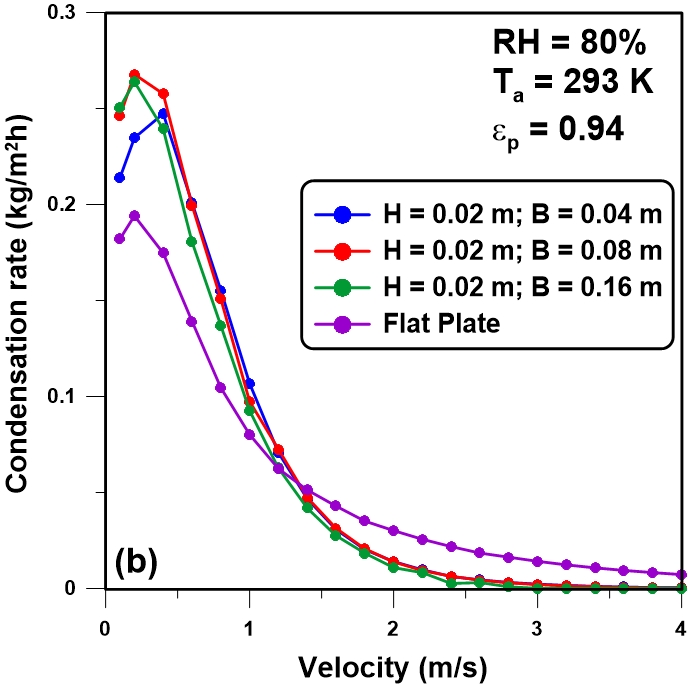
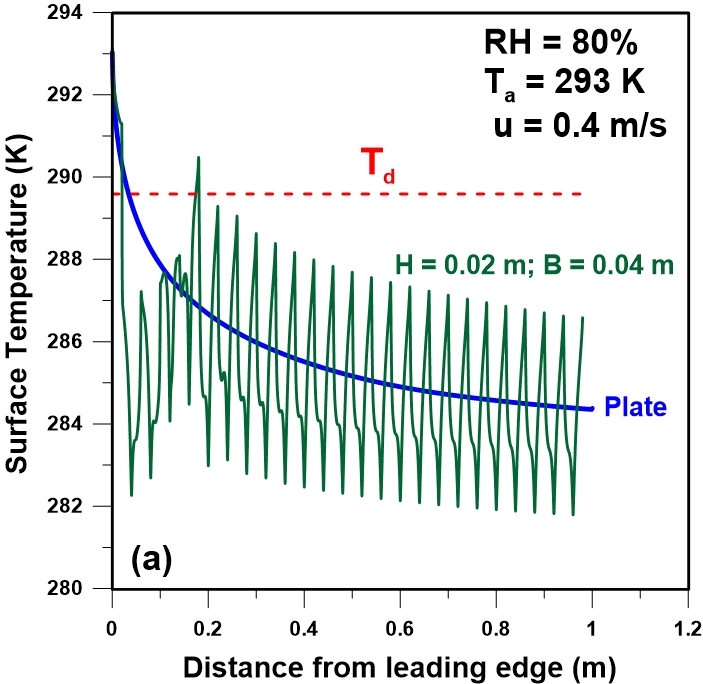
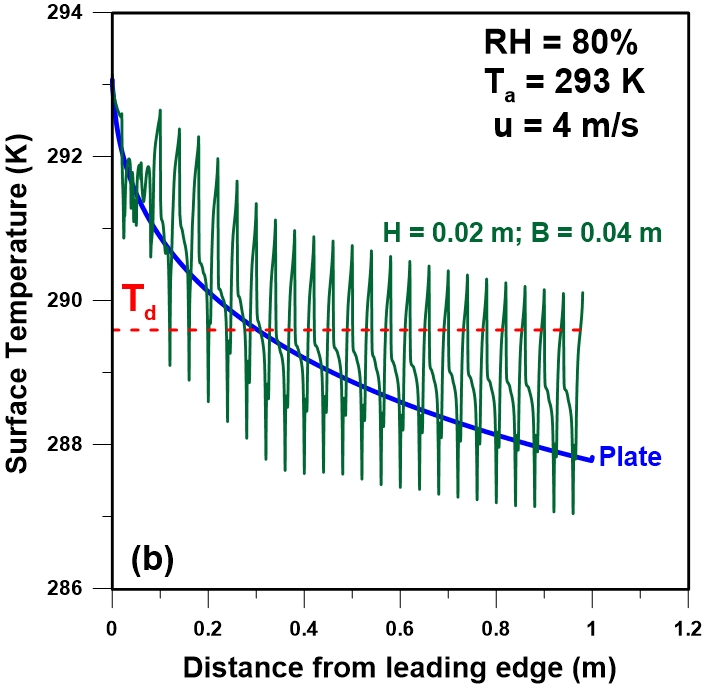
Figure 11(a-b) presents the temperature profile of a flat plate condenser and a triangularly-corrugated condenser at the wind speed of 0.4 m/s and 4 m/s. When the wind speed is low, the surface temperature decreases rapidly (Figures 11a) due to the air collision to the top of the triangular corrugations and the flow deviation that reduce the wind speed near the surface. This decrease is significant at lower wind speed whereas at higher wind speeds this decrease is small and the decrease in the convective heat transfer is not important. This explains the higher rate of condensation at lower wind speed for this type of collector in comparison to the flat plate condenser. However, similar condensation rates are obtained at higher wind speed (Fig. 10). Since it was assumed that the conductivity of the plate was negligible, the local variation of the temperature along the grooves of the corrugated plate is adopting a repeating temperature pattern with an average value that follows very closely the decreasing flat plate temperature. However, the temperature for the first portion of the corrugated plate is lower than the flat plate temperature prior to assuming a more uniform and decreasing pattern. This initial lower temperature will favour a higher condensation when the plate temperature is below the dew point.

The rate of condensation obtained with the flat plate and corrugated plates was compared to the water collection rate that would be achieved with a 1-m V-shape collector. Figures 12 presents the condensation rate for the V-shape collector, the planar condenser and the best triangularly-corrugated surface for different wind speeds, air temperature of 293 K and relative humidity of 80%. Results show that when the wind speed is less than 1 m/s, the condensation rate with the corrugated surface is larger than the condensation rate with the other two geometries. When the wind speed increases, the rate of condensation initially increases before reaching a maximum at relatively low wind speeds and then progressively decreased thereafter. Indeed, according to these results, all water collectors are more efficient when the wind speed is in the range of 0.5 to 1 m/s.

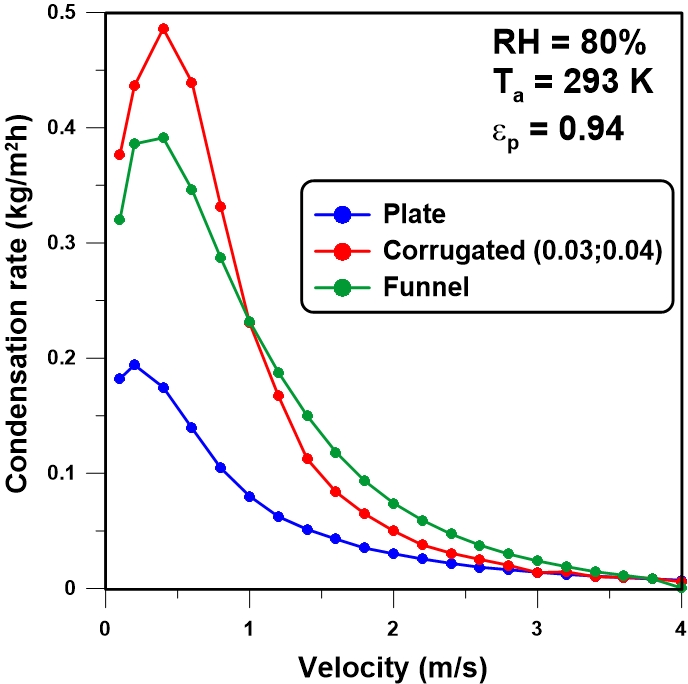
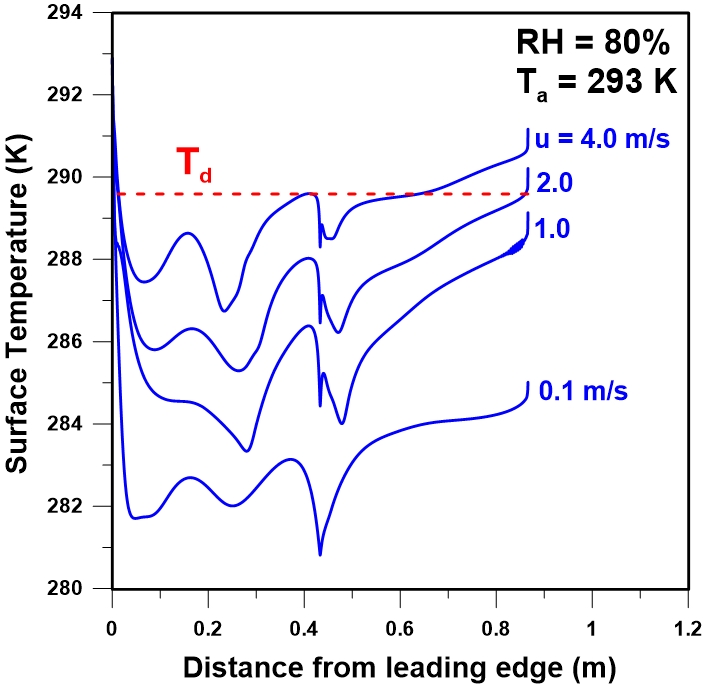
Figure 13 shows the variation in the surface temperature for five different wind speeds when the ambient air temperature is 293 K with a relative humidity of 80%. As expected, the surface temperature on the upwind side is lower than the temperature on the downwind side of the V-shape collector. An increase in the wind speed leads to an increase in the surface temperature caused by the increase of in the convective heat transfer.

4. Conclusion

A numerical investigation was carried out to assess the atmospheric conditions and some plate properties that may affect water harvesting using a horizontal plate condenser exposed to clear night sky conditions. Generally, the surface temperature of the passive plate collector is a trade-off between radiation heat transfer responsible for cooling, convection heat transfer for heating, and also heat associated with condensation. It was found that the wind speed, the relative humidity, the air temperature and the plate emissivity all have an impact on the ability of a plate to condense water vapour. Numerical results highlighted the significant role of the wind speed which increases the forced convection heat transfer and leading to an increase in the plate temperature. On the other hand, increasing the air velocity increases the mass transfer rate, resulting in higher vapour condensation rate. A higher percentage relative humidity increases the dew point temperature which favours the potentiality of water collection but, on the other hand, also leads to a slight increase in the plate temperature. Combination effects cause higher vapour condensation rate for the case of higher relative humidity.

For a constant relative humidity, the air temperature affects the plate temperature and the vapour condensation rate. For higher ambient temperature, the plate temperature increases and the potential to collect water decreases. On the other hand, at lower temperature the plate temperature is much lower but the amount of moisture in the air is also much lower such that the condensation decreases. These two opposing effects give rise to a maximum condensation rate at a given temperature.

Air temperature and relative humidity are environmental variables which greatly vary throughout the year and from one geographic location to another. The only design-dependent variable that can be changed to improve passive water collectors is the wind speed as seen by the surface. In order to reduce air contact with the surface, V-shape collector and triangularly-corrugated surfaces were proposed and simulated for their ability to collect water. Results show that the condensation rate for the triangularly-corrugated surface is greater than for the flat plate condenser, especially at lower wind speeds. For higher wind speeds, the water collection rate is low for all collector geometries. When the wind speed is less than 1 m/s, the water yield for triangularly-corrugated surface is higher for than the V-shape collector.

Nomenclature
A	Plate surface area (m2)
B	Dimension of the base of corrugations (m)
DAB	Mass diffusivity (m2/s)
hx	Local heat transfer coefficient at a distance x from the edge (kJ/m2 s K)
H	Air humidity (kg H2O/kg dry air) or height of corrugations (m)
k	Thermal conductivity (J/m s K)
kx	Local mass transfer coefficient (mol/m2s)
M	Molecular weight (kg/kmol)
P	Ambient pressure (kPa)
Pr	Prandtl number (dimensionless)
q”	Heat transfer rate (W)
Re	Reynold number (dimensionless)
RH	Relative humidity (dimensionless)
Sc	Schmidt number (dimensionless)
T	Temperature (oC or K)
u	Wind speed (m/s)
x	Distance from the leading edge (m)
ε	Emissivity (dimensionless)
σ	Stefan-Boltzmann constant (5.67 ×10-8 W/m2K4)
b	Constant (17.62, dimensionless)
n	Kinematic viscosity (m2/s)
l	Constant (515.27 K)
lw	Latent heat of condensation of water (kJ/kg)
Subscripts
a	Air
conden	Condensation
conv	Convention
d	Dew point
p	Plate
rad	Radiation
s	Sky
x	Distance from the leading edge (m)