Volume 5 - Year 2018 - Pages 1-9
DOI: 10.11159/jffhmt.2018.001
Natural Convection in an Annular Enclosure: Influence of Magnetic Field-dependent Thermal Conductivity on Heat Transfer
Mohammadhossein Hajiyan, Shohel Mahmud, Mohammad Biglarbegian, Hussein A. Abdullah
School of Engineering, University of Guelph
50 Stone Rd. East, Guelph, Ontario, Canada N1G2W1
Mhajiyan@uoguelph.ca, Smahmud@uoguelph.ca, Mbiglarb@uoguelph.ca, Habdulla@uoguelph.ca
Abstract - In this paper, the natural convection heat transfer characteristics are investigated inside an annular enclosure containing Magnetic Nanofluid (MNF) (i.e., Fe3O4 nanoparticles are dispersed in Kerosene). A uniform magnetic field (H) is applied along the axial direction of the enclosure. Magnetic field-dependant thermal conductivity (k) of the MNF is considered as a nonlinear function which is interpolated from the experimental results. Finite element method is utilized to solve the governing equations for various magnetic field strengths, volume fractions of MNF, and Rayleigh numbers. Average Nusselt numbers along the hot wall are calculated and compared for different scenarios. The results show that the applied magnetic field has a significant effect on the heat transfer rate, more specifically on the Nusselt number, in the enclosure for higher volume fractions of nanoparticles. Thermal conductivity enhancement as a result of using magnetic field can be used for various applications such as thermal energy storage in which the heat transfer needs to be accurately controlled.
Keywords: Magnetic nanofluid (MNF), Magnetic Field-dependant thermal conductivity, Lorentz force, Natural convection.
© Copyright 2018 Authors - This is an Open Access article published under the Creative Commons Attribution License terms Creative Commons Attribution License terms. Unrestricted use, distribution, and reproduction in any medium are permitted, provided the original work is properly cited.
Date Received: 2017-10-12
Date Accepted: 2018-01-24
Date Published: 2018-03-05
- Nomenclature
- B Magnetic flux density [T]
- Bz Component of magnetic flux density
- Cp Heat capacitance at constant temperature [J/kg.K]
- Dp Diameter of nanoparticles [nm]
- D Thickness of nanofluid in radial direction [m]
- E Electrical field [V/m]
- J Current density [A/m2]
- K Pyromagnetic coefficient
- K Thermal conductivity [W/m.K]
- L Characteristic Length [m]
- M Magnetization respect to temperature
- T Temperature [K]
- r, z Space coordinates [m]
- u, v Velocity components [m/s]
- Greek symbols
- α Thermal diffusivity [m2 /s]
- β Coefficient of thermal expansion [1/K]
- χ Magnetic Susceptibility
- ν Kinematic viscosity [m2 /s]
- µ Dynamic viscosity [kg/ms]
- σ Electrical conductivity [(Ω.m)−1 ]
- ρ Density [kg/m3]
- φ Volume fraction [%]
- Subscripts
- c Cold
- h Hot
- cu Curie
- f Fluid
- s Solid
- nf Nanofluid
1. Introduction
Heat transfer enhancement has been a challenging topic for researchers for many years to enhance the efficiency of many applications such as cooling and electronic equipment and solar systems. Numerous studies have been carried out on passive and active heat transfer systems to increase their efficiencies [1]. One of the effective ways to improve the heat transfer rate in fluids is adding conductive nanoparticle to the fluid [2].
Adding nanoparticles to the base fluid can change the thermophysical properties of nanofluids. To have more control on the properties of nanofluids, magnetic nanofluids (MNF), which consist of magnetic nanoparticles in a base fluid, are introduced. The application of magnetic fields caused nanoparticles to aggregate in the carrier fluid, creating highly conductive paths for the heat flow inside the convective heat transfer environment. Therefore, the thermal conductivity of the nanofluid enhances. Several studies reported that having nanoparticles with higher thermal conductivity can enhance the heat transfer rate [3, 4]. However, in another study when Fe nanoparticles and Cu nanoparticles were examined and compared, it was indicated that adding conductive nanoparticle is not always the most effective way to improve the conductivity [5].
The main advantage of having magnetic nanoparticles is the capability to control thermophysical properties using external magnetic fields [6]. The use of MNF creates opportunities in different applications such as electrical application, thermal engineering systems, heat exchanger designs, thermal energy storage systems, and thermal batteries or medical applications such as Magnetic Resonance Imaging (MRI) enhancement and bioseparation for targeted cancer treatment [7-10]. Magnetic nanoparticles are suspended in the carrier/base fluid and subjected to the gravitational and magnetic fields; thus, the particle sedimentation is a factor that has to be taken into account [11]. The percentage of nanoparticles inside the carrier fluid is very important. Moreover, the interaction forces between nanoparticles, which cause Brownian motion, directly depend on size of the nanoparticle.
Tynjala and Ritvanen [12] studied the thermo-magnetic convection of MNF in annulus enclosure. The effect of gravity, which causes the buoyancy force, and magnetic field were numerically investigated. The results showed that the average Nusselt number increased when Rayleigh number increased [12]. Experimental and theoretical studies were conducted on thermal conductivity and viscosity by Murshed et. al., [13]. In [13], it was found that the thermal conductivity strongly depends on the temperature. They also proposed the model to accurately estimate the thermal conductivity with only 2% error [13]. In an experimental study by Pastoriza-Gallego et. al. [14], the volumetric behaviours of iron oxide nanofluids and enhancement of thermal conductivity were investigated. It was reported that the enhanced thermal conductivity is a function of volume fraction and does not depend on temperature (up to 1% volume fraction of the nanoparticle) [14]. Ashorynejad et. al., numerically investigated the effects of magnetic field on a cylindrical annulus filled with Ag-water nanofluid when a radial magnetic field was used parallel to temperature gradient [15]. It was reported that the average Nusselt number increased when volume fraction/Rayleigh number increased; however, it was a decreasing function of Hartmann number [15]. Two-phase simulation of nanofluid in an annulus subjected to the axial magnetic field was studied by Sheikholeslami and Abelman [16]. A reduced model (ODE) of the geometry in their study was solved numerically and the results showed a direct relationship between Nusselt number and Hartmann number, but reverse relationship with Reynolds number and Brownian parameter [16]. In much of literature, the applied magnetic field was assumed constant and uniform. However, in the study conducted by Sheikholeslami et. al., forced convection heat transfer in a semi-annulus geometry was studied when a variable magnetic field was used [17]. In [17], Fe3O4-water was used as MNF and the thermal conductivity was estimated using Maxwell-Garnett (MG) model. Results showed that for high Rayleigh numbers, the effects of Kelvin body forces are notable [17].
Based on the literature on MNF, thermal conductivity is an
important parameter to improve the heat transfer rate. To the best knowledge of
the authors, no numerical study is conducted in which thermal conductivity was a
function of both magnetic field and volume fraction![]() . Thus, as a continuation of our
previous work [18], the motivation of this study was to investigate the
development of heat transfer inside the annular enclosure filled with MNF in
which the thermal conductivity of MNF is a nonlinear function of both magnetic
field and volume fraction.
. Thus, as a continuation of our
previous work [18], the motivation of this study was to investigate the
development of heat transfer inside the annular enclosure filled with MNF in
which the thermal conductivity of MNF is a nonlinear function of both magnetic
field and volume fraction.
In this study, we proposed the annular enclosure filled with kerosene-Fe3O4 when the thermal conductivity was a nonlinear function of both magnetic field and volume fraction. The proposed enclosure is subjected to the uniform magnetic field. Natural convection of MNF inside the enclosure for various Rayleigh numbers was studied.
The rest of the paper is organized as follows: Section 2 defines the problem, the geometry of enclosure, and assumptions. Section 3 provides governing equations and boundary conditions. Section 4 describes the numerical procedure in details to solve the governing equations followed by Section 5 that reports the results and discusses the findings in this study. Finally, Section 6 concludes the paper.
2. Geometry and Properties
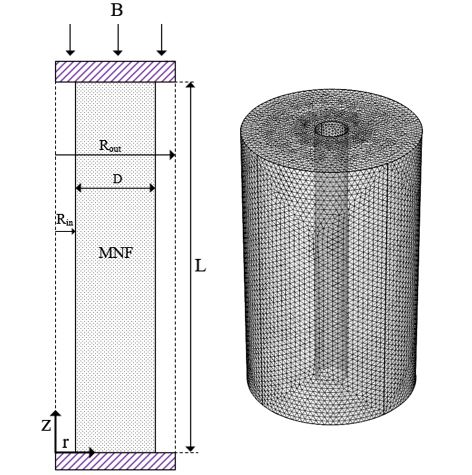
Figure 1 shows the enclosure filled with MNF (kerosene and Fe3O4). The material of the enclosure is acrylic glass and the inner pipe is copper. The bottom and top of the annulus are adiabatic. The properties of pure kerosene and Fe3O4 are provided in Table.1
Table 1. Properties of kerosene and Fe3O4 [19, 20].
| ρ | Cp | 𝑘 | dp | σ | µ | β | |
| Kerosene | 788 | 2010 | 0.129 | - | 5e-11 | 1.64e-3 | 8e-4 |
| Fe3O4 | 5200 | 670 | 6 | 47 | 25000 | - | 1.3e-5 |
The thermophysical properties
of MNF, except thermal conductivity (![]() ), are calculated using classical
models as follows [20-22]:
), are calculated using classical
models as follows [20-22]:
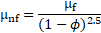
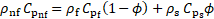
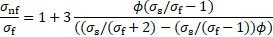
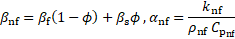
Note that in Eq. 4, ![]() is a function of magnetic field and
volume fraction of nanoparticles and obtained experimentally by [23].
is a function of magnetic field and
volume fraction of nanoparticles and obtained experimentally by [23].
3. Mathematical Modelling and Boundary Conditions
In this study, it is assumed that the flow is laminar and steady,
and the MNF is incompressible. In addition, the effect of Brownian motion is
neglected. The cylindrical coordinates system of (![]() ) that represents the velocity
components of (
) that represents the velocity
components of (![]() ) are illustrated in Figure 1. To
simulate the heat transfer through the magnetic nanofluid and by assuming
Boussinesq approximation, the conservation of mass, momentums, and energy
equations are as follows:
) are illustrated in Figure 1. To
simulate the heat transfer through the magnetic nanofluid and by assuming
Boussinesq approximation, the conservation of mass, momentums, and energy
equations are as follows:
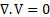
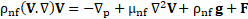
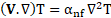
The Electric potential and Lorentz force which depend on the electrical conductivity of the MNF and velocity of nanoparticles, are calculated as follows:
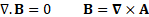
where ![]() is the magnetic field intensity (A/m)
and B is the magnetic flux density (
is the magnetic field intensity (A/m)
and B is the magnetic flux density (![]() ).
It is assumed that the magnetic field is uniform and azimuthally symmetric only
along
).
It is assumed that the magnetic field is uniform and azimuthally symmetric only
along ![]() . In this case, we only have
. In this case, we only have ![]() in
in ![]() direction as the magnetic field is applied perpendicular to the temperature gradient. In
our simulation, we assumed no slip-velocity condition on the walls. The hot
surface is the copper pipe where the hot fluid passes through and the cold
surface is the acrylic glass. Having steady single phase flow inside the
enclosure and thermal insulations on the top and the bottom of the enclosure,
we have the following boundary condition:
direction as the magnetic field is applied perpendicular to the temperature gradient. In
our simulation, we assumed no slip-velocity condition on the walls. The hot
surface is the copper pipe where the hot fluid passes through and the cold
surface is the acrylic glass. Having steady single phase flow inside the
enclosure and thermal insulations on the top and the bottom of the enclosure,
we have the following boundary condition:
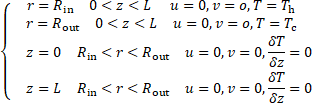
where L is the height of the
enclosure (3.5 in) and the thickness of the MNF in a radial direction (![]() ) is 22.24 mm . Using polynomial curve
fitting method, we obtained the thermal conductivity as a function of both
volume fraction
) is 22.24 mm . Using polynomial curve
fitting method, we obtained the thermal conductivity as a function of both
volume fraction ![]() and magnetic field (
and magnetic field (![]() from the literature [24]. In our
numerical study, we chose five different volume fractions (1.115%, 1.7%, 2.23%,
3.465%, and 4.7%). Also, the reference velocity and thermal thickness are
expressed as follows [25]:
from the literature [24]. In our
numerical study, we chose five different volume fractions (1.115%, 1.7%, 2.23%,
3.465%, and 4.7%). Also, the reference velocity and thermal thickness are
expressed as follows [25]:
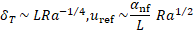
where ![]() is the thermal thickness
and
is the thermal thickness
and ![]() is a thermal diffusivity
of MNF. Moreover, the stream function
is a thermal diffusivity
of MNF. Moreover, the stream function ![]() is defined as
is defined as ![]() and
and ![]() . Thus, the stream
function which satisfies the governing equations for the annular geometry is as
follows:
. Thus, the stream
function which satisfies the governing equations for the annular geometry is as
follows:
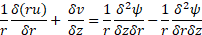
subject to ![]() and
and ![]() for initial condition. Note that the
formulation in Eq. 11 satisfies the continuity where
for initial condition. Note that the
formulation in Eq. 11 satisfies the continuity where ![]() =0. To compare and validate our
simulation results with previous studies in which Ra versus Nu is provided (no
magnetic field and no nanoparticles), we defined the Rayleigh number as
=0. To compare and validate our
simulation results with previous studies in which Ra versus Nu is provided (no
magnetic field and no nanoparticles), we defined the Rayleigh number as ![]() and the local Nusselt number on the
hot surface is defined as follows:
and the local Nusselt number on the
hot surface is defined as follows:
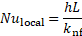
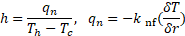
where ![]() is
effective length,
is
effective length, ![]() is
the heat transfer coefficient, and
is
the heat transfer coefficient, and ![]() is normal heat flux from the wall.
Finally, by substituting Eq. 13 into Eq. 12, we calculated the average Nusselt
number along the hot wall as follows:
is normal heat flux from the wall.
Finally, by substituting Eq. 13 into Eq. 12, we calculated the average Nusselt
number along the hot wall as follows:
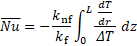
where ![]() ,
, ![]() is thermal conductivity of fluid
obtained from Table.1, and
is thermal conductivity of fluid
obtained from Table.1, and ![]() is a polynomial function of both
magnetic field and volume fraction of nanoparticles.
is a polynomial function of both
magnetic field and volume fraction of nanoparticles.
4. Numerical Procedure and Grid Testing
In this study, we used finite element method (FEM) to solve the
governing equations. We used direct solver method for three fully coupled
modules (heat transfer in solid, fluid and laminar flow) and solved numerically
with the commercial COMSOL Multiphysics software (4.3b). The convergence was
set to be ![]() for termination criteria, and linear
approximation was assumed within the elements. In order to validate the
numerical scheme and accuracy of the simulation, the Nusselt number is
calculated when the Prandtl number (Pr) is 0.7. Our simulation results showed
the good agreement when they were validated against the previous literature in
Figure. 2.
for termination criteria, and linear
approximation was assumed within the elements. In order to validate the
numerical scheme and accuracy of the simulation, the Nusselt number is
calculated when the Prandtl number (Pr) is 0.7. Our simulation results showed
the good agreement when they were validated against the previous literature in
Figure. 2.

 , and H=60 ×
, and H=60 ×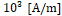 ).
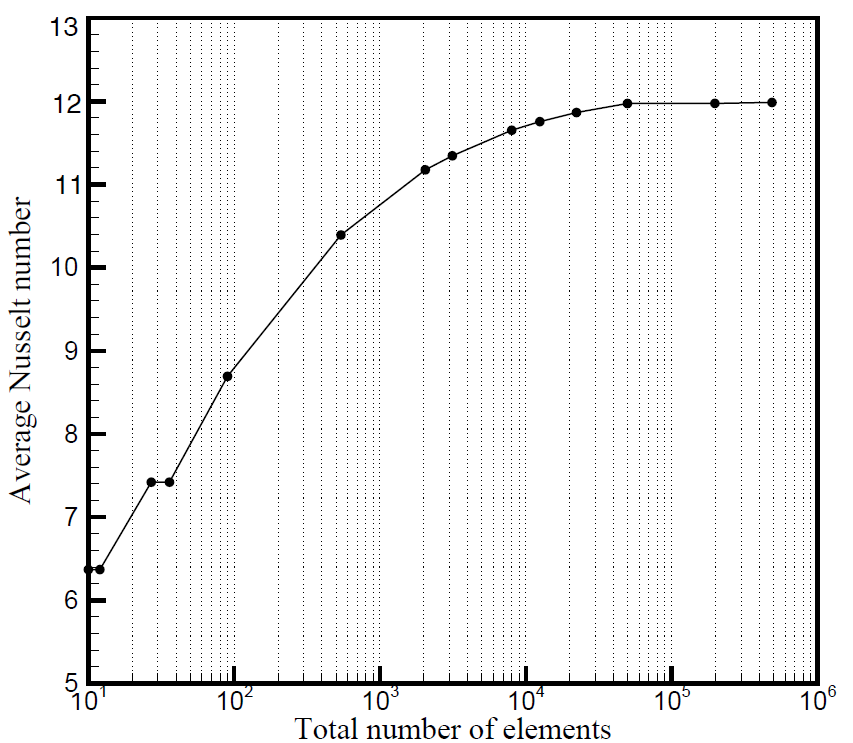
).To ensure the grid independency in our simulation results, we used different element sizes (various grid in z and r directions) and computed the average Nusselt number. Figure 3 illustrates the average Nusselt number along the hot wall versus total number of elements. Based on our results in Figure 3, the total number of 22275 (75 × 297) provided the sufficient accuracy and beyond this point, the results did not change significantly. Thus, we used this number of elements to compute our results in this study.
5. Results and Discussion
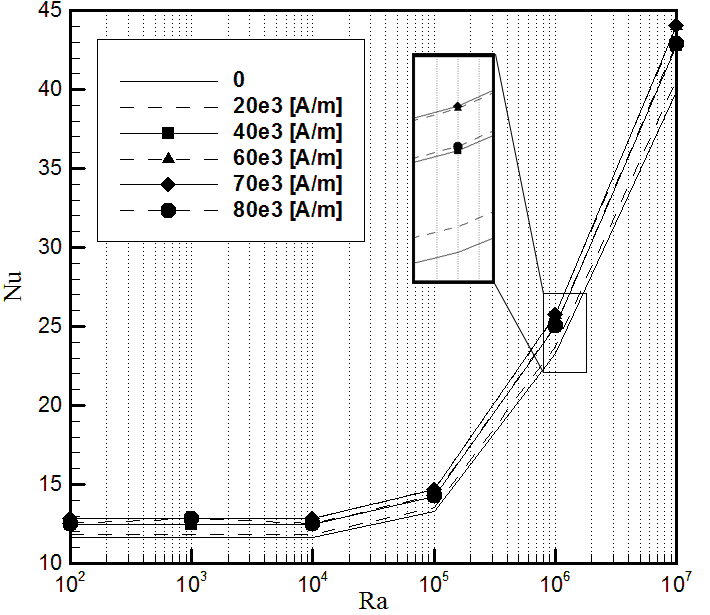
Effects of the uniform transverse magnetic field on heat transfer distribution inside the annular enclosure filled with kerosene- Fe3O4 is investigated. Figure 4-Figure 6 show the effect of magnetic field on the average Nusselt number when Rayleigh is changing from 104 to 107 for various volume fractions (1.115%, 1.7%, 2.23%, 3.465% , and 4.7%), and magnetic fields (0-80×103 [A/m]). As it can be seen from Figure 4 - Figure 6, the Nu is an increasing function of volume fraction. Also, increasing the magnetic field with higher volume fractions result in increasing the Nusselt number. However, a slight decrease is observed for high volume fractions at/about 70×103 [A/m] which can be explained by the atomic motion of the particles and induction heating which was occurred inside the enclosure exposed to the external magnetic field.
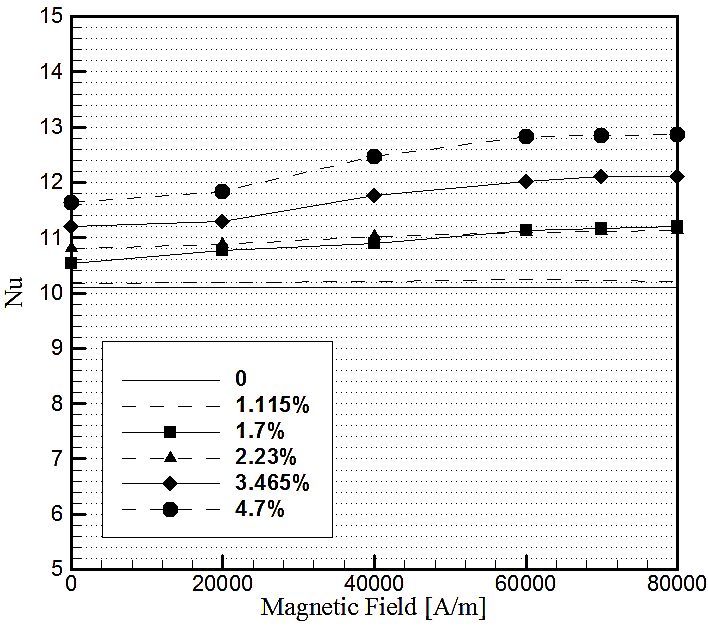
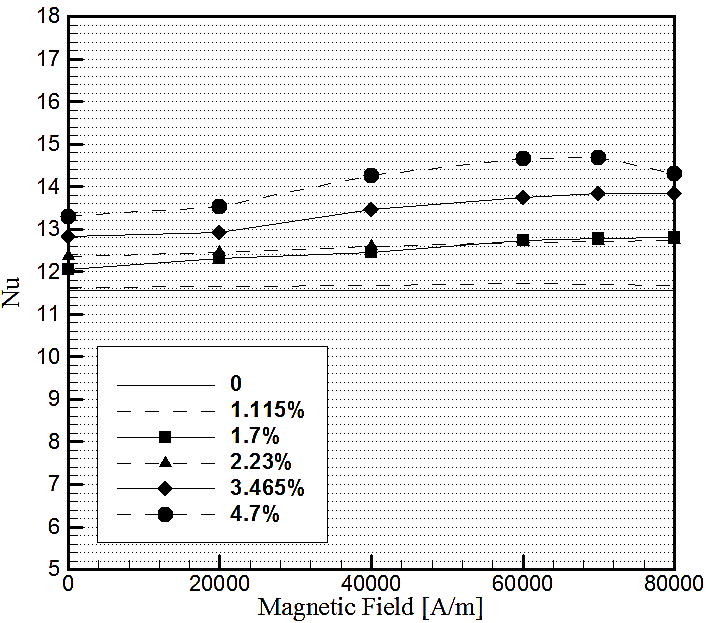
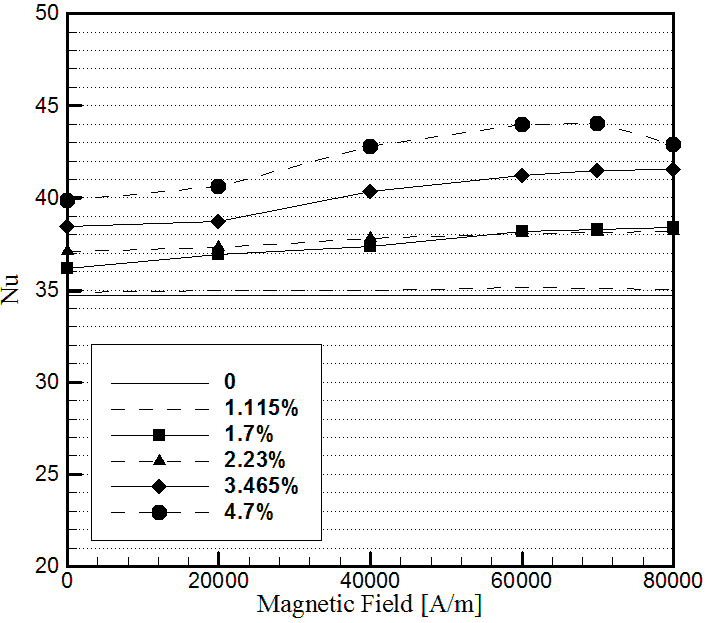
The main contribution of this study is depicted in Figure 7 and Figure 8 for two specific volume fractions (φ=1.115% and φ=4.7%. Figure 7 shows the relative Nusselt number which is calculated as follow:
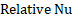 =
=
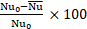
where Nu0 is the
average Nusselt number without any magnetic field (![]() = 0). Both figures show that the
average Nusselt number increases with increasing Rayleigh number. The variation
of Nu in the presence of the magnetic field is notable for magnetic nanofluid
with a high volume fraction of nanoparticle. Due to the fact that the magnetic
field affects the thermal conductivity; this effect became noticeable for the
high volume fraction of MNF. Note that the MNF can be saturated due to the high
applied magnetic field. This phenomenon can be seen easily in Figure 7 where
the highest relative Nu obtained when the applied magnetic field is 60×103
[A/m].
= 0). Both figures show that the
average Nusselt number increases with increasing Rayleigh number. The variation
of Nu in the presence of the magnetic field is notable for magnetic nanofluid
with a high volume fraction of nanoparticle. Due to the fact that the magnetic
field affects the thermal conductivity; this effect became noticeable for the
high volume fraction of MNF. Note that the MNF can be saturated due to the high
applied magnetic field. This phenomenon can be seen easily in Figure 7 where
the highest relative Nu obtained when the applied magnetic field is 60×103
[A/m].
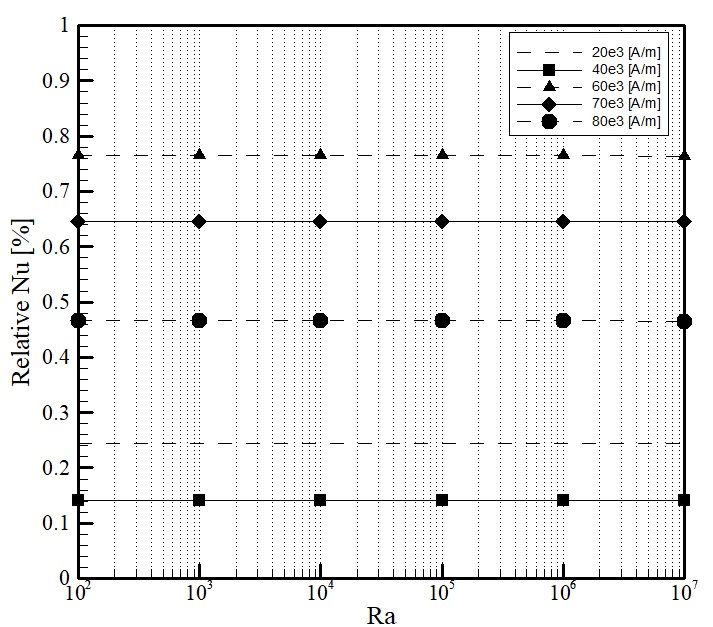
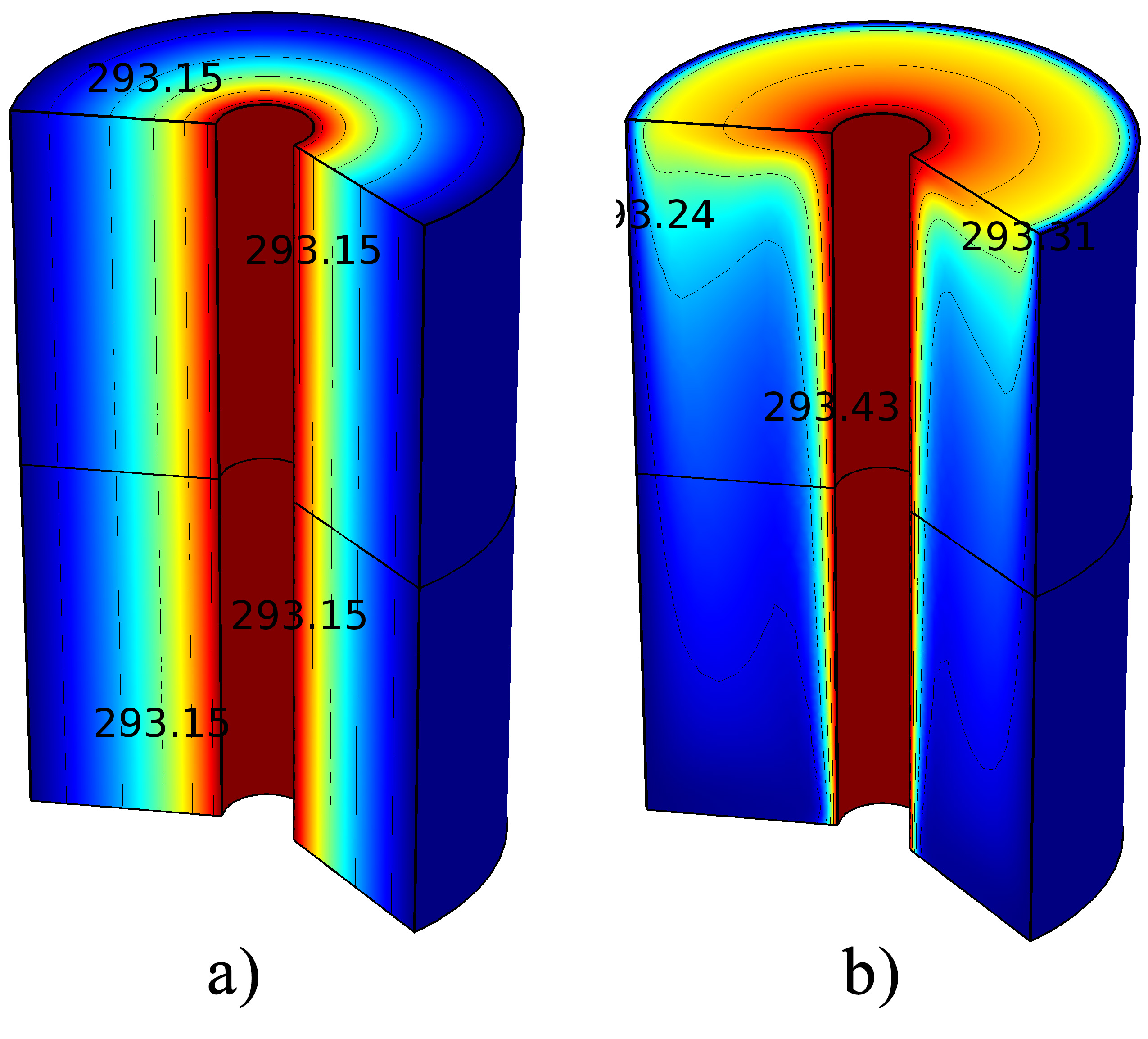
Figure 9 illustrates the temperature distribution for different Rayleigh numbers when φ = 4.7% and H=80×103 [A/m]. In Figure 9 (a), when Ra is 102, the uniform temperature distribution is observed along the radius of the enclosure while in (b), where Ra=107, the effect of buoyancy force on natural convection inside the enclosure is dominant.
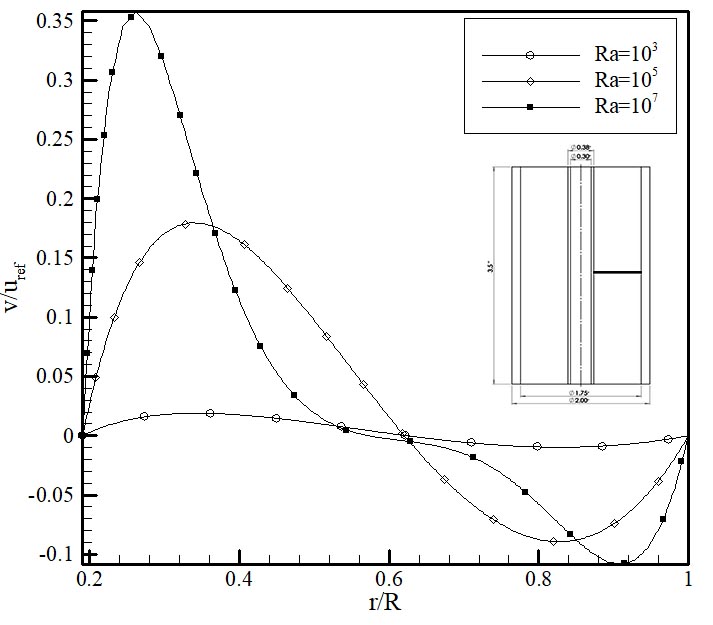
In Figure 10, the variation of the dimensionless velocity inside the enclosure is depicted along the radial distance at the centre of the enclosure. It can be observed that the variation of velocity for higher Rayleigh numbers is more pronounced. The applied magnetic field affected the velocity and consequently convective heat transfer inside the enclosure. Since this effect is very small, it cannot be visualized. Thus, the average Nusselt numbers at the hot wall for different Ra and H are tabulated in Table 2. According to Table 2, the average Nusselt number is an increasing function of the magnetic field. Note that the Nusselt number slightly dropped at/beyond 90×103 [A/m]; this decrease in Nu can be explained by the deformation of chain-like structures of nanoparticles inside the enclosure in the presence of the high-intensity magnetic fields. Another reason for the decrease in Nu beyond 90×103 [A/m] is the application of strong magnetic fields which can internally heat up the MNF (Joule heating) and has an impact on the average Nusselt number.
Table 2. Average Nusselt number for different Ra and magnetic fields (![]() =
3.465%).
=
3.465%).
| H[A/m] | |||||
| Ra | 10×103 | 30×103 | 50×103 | 70×103 | 90×103 |
| 102 | 11.428 | 11.744 | 12.318 | 12.460 | 11.969 |
| 103 | 11.428 | 11.745 | 12.318 | 12.460 | 11.970 |
| 104 | 11.453 | 11.770 | 12.345 | 12.487 | 11.995 |
| 105 | 13.065 | 13.426 | 14.082 | 14.244 | 13.684 |
| 106 | 22.721 | 22.350 | 24.489 | 24.771 | 23.797 |
| 107 | 38.100 | 39.153 | 41.061 | 41.533 | 39.902 |
Figure 11 shows the comparison between streamlines for different
Rayleigh numbers and volume fraction of nanoparticles when magnetic field varies.
Although the streamline patterns stayed the same for each Rayleigh number, the
stream function values decreased in the presence of magnetic field (Table. 3).
Note that the changes of stream function values in low Ra are small; this
decrease is quite notable in high Rayleigh numbers. Table 3 shows the variation
of stream function (![]() ) for various Ra and magnetic fields.
From Table 3 and Figure 11, it can be concluded that strong magnetic field
affected the Buoyancy driven flow and significantly decreased the velocity of
the flow.
) for various Ra and magnetic fields.
From Table 3 and Figure 11, it can be concluded that strong magnetic field
affected the Buoyancy driven flow and significantly decreased the velocity of
the flow.
Figure 12 illustrates the isotherms for Ra=103, Ra=104, Ra=105, Ra=106, and Ra=107. The results show the conduction and convection regimes for low and high values of Ra, respectively. From Figure 12, it can be concluded that for small values of Rayleigh the conduction like flow was dominant, while for higher values of Rayleigh the convection like regime was observed.
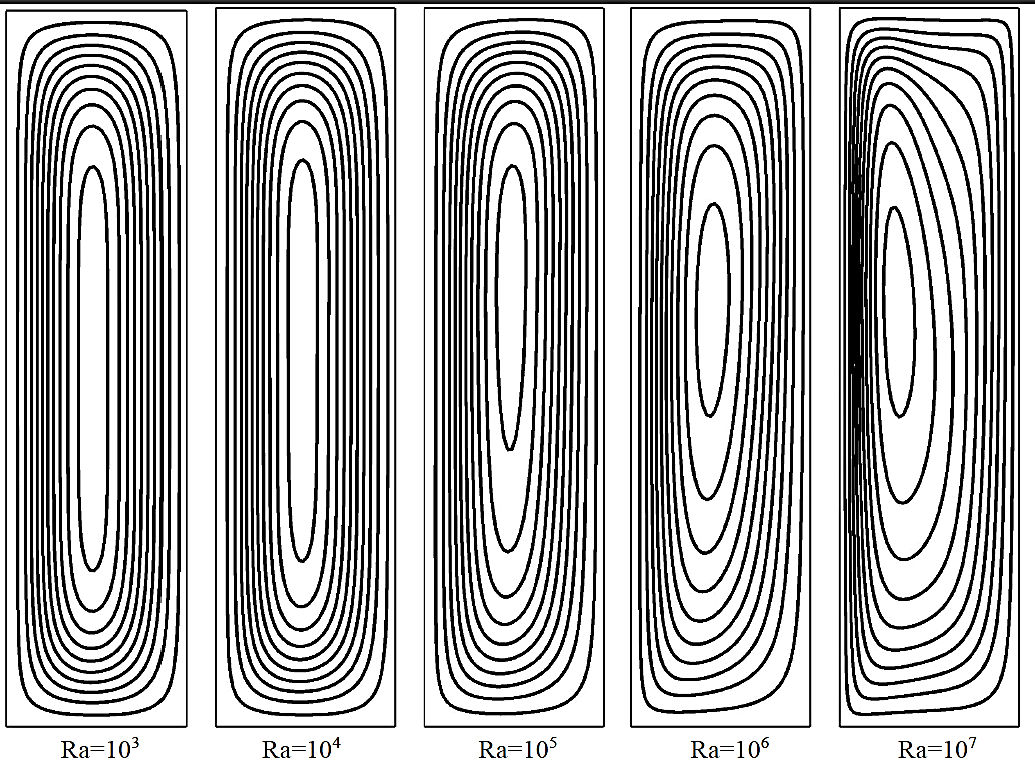
Table 3. Variation of stream function values versus Rayleigh number (φ=3.465%).
| H\Ra | 103 | 104 | 105 | 106 | 107 |
| 10×103 | 0.000021 | 0.002086 | 0.019918 | 0.074701 | 0.101500 |
| 30×103 | 0.000021 | 0.002086 | 0.019919 | 0.074716 | 0.101474 |
| 50×103 | 0.000021 | 0.002086 | 0.019920 | 0.074745 | 0.101427 |
| 70×103 | 0.000021 | 0.002086 | 0.019921 | 0.074752 | 0.101416 |
| 90×103 | 0.000021 | 0.002086 | 0.019919 | 0.074728 | 0.101455 |

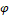 Kerosene with Fe3O4
Kerosene with Fe3O4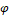 =3.465%
(H=70×103).
=3.465%
(H=70×103).6. Conclusion
In this paper, we investigated the effect of the transverse magnetic field on the annular enclosure filled with magnetic nanofluid (kerosene-Fe3O4). Nonlinear relationships between thermal conductivity and magnetic field were obtained and used as polynomial functions for MNF property. Variation of the average Nusselt number along the hot wall was studied for different magnetic field intensities. Heat transfer rate enhanced significantly when the thermal conductivity was a function of magnetic field and volume fraction instead of a constant value. The results show the increase of magnetic fields strength and Rayleigh number both lead to increase the Nusselt number, significantly.
References
[1] I. Nkurikiyimfura, Y. Wang, and Z. Pan, “Heat transfer enhancement by magnetic nanofluids-a review,” Renewable and Sustainable Energy Reviews, vol. 21, pp. 548-561, 2013. View Article
[2] H. Ozoe and K. Okada, “The effect of the direction of the external magnetic field on the three-dimensional natural convection in a cubical enclosure,” International Journal of Heat and Mass Transfer, vol. 32, no. 10, pp. 1939-1954, 1989. View Article
[3] J. Philip, P. Shima, and B. Raj, “Enhancement of thermal conductivity in magnetite based nanofluid due to chainlike structures,” Applied Physics Letters, vol. 91, no. 20, p. 203108, 2007. View Article
[4] G. Huminic, A. Huminic, I. Morjan, and F. Dumitrache, “Experimental study of the thermal performance of thermosyphon heat pipe using iron oxide nanoparticles,” International Journal of Heat and Mass Transfer, vol. 54, no. 1, pp. 656-661, 2011. View Article
[5] T.-K. Hong, H.-S. Yang, and C. Choi, “Study of the enhanced thermal conductivity of nanofluids,” Journal of Applied Physics, vol. 97, no. 6, p. 064311, 2005. View Article
[6] A. Jafari, T. Tynjala, S. Mousavi, and P. Sarkomaa, “CFD simulation and evaluation of controllable parameters effect on thermomagnetic convection in ferrofluids using taguchi technique,” Computers Fluids, vol. 37, no. 10, pp. 1344-1353, 2008. View Article
[7] D. Wen, G. Lin, S. Vafaei, and K. Zhang, “Review of nanofluids for heat transfer applications,” Particuology, vol. 7, no. 2, pp. 141-150, 2009. View Article
[8] A. Ito, M. Shinkai, H. Honda, and T. Kobayashi, “Medical application of functionalized magnetic nanoparticles,” Journal of bioscience and bioengineering, vol. 100, no. 1, pp. 1-11, 2005. View Article
[9] G. Pooja, “Magnetic nanoparticles enhance medical imaging,” The Journal of Young Investigators, vol. 15, no. 2, 2006.
[10] J.-J. Chieh, S.-J. Lin, and S.-L. Chen, “Thermal performance of cold storage in thermal battery for air conditioning,” International journal of refrigeration, vol. 27, no. 2, pp. 120-128, 2004. View Article
[11] H. Engler, D. Borin, and S. Odenbach, "Thermomagnetic convection influenced by the magnetoviscous effect,” Journal of Physics: Conference Series, IOP Publishing, vol. 149, p. 012105, 2009. View Article
[12] T. Tynjala and J. Ritvanen, “Simulations of thermo-magnetic convection in an annulus between two concentric cylinders,” 2004.
[13] S. Murshed, K. Leong, and C. Yang, “Investigations of thermal conductivity and viscosity of nanofluids,” International Journal of Thermal Sciences, vol. 47, no. 5, pp. 560-568, 2008. View Article
[14] M. Pastoriza-Gallego, L. Lugo, J. Legido, and M. Pi˜neiro, “Enhancement of thermal conductivity and volumetric behaviour of fexoy nanofluids,” Journal of Applied Physics, vol. 110, no. 1, p. 014309, 2011. View Article
[15] H. R. Ashorynejad, A. A. Mohamad, and M. Sheikholeslami, “Magnetic field effects on natural convection flow of a nanofluid in a horizontal cylindrical annulus using lattice Boltzmann method,” International Journal of Thermal Sciences, vol. 64, pp. 240-250, 2013. View Article
[16] M. Sheikholeslami and S. Abelman, “Two-phase simulation of nanofluid flow and heat transfer in an annulus in the presence of an axial magnetic field,” IEEE Transactions on Nanotechnology, vol. 14, no. 3, pp. 561-569, 2015. View Article
[17] M. Sheikholeslami, K. Vajravelu, and M. M. Rashidi, “Forced convection heat transfer in a semi annulus under the influence of a variable magnetic field,” International Journal of Heat and Mass Transfer, vol. 92, pp. 339-348, 2016. View Article
[18] M. Hajiyan, S. Mahmud, M. Biglarbegian, and H. A. Abdullah, “Natural convection in an enclosure: Effect of magnetic field dependent thermal conductivity,” in Proceedings of the 4th International Conference of Fluid Flow, Heat and Mass Transfer (FFHMT’17), 2017. View Article
[19] W. Yu, H. Xie, L. Chen, and Y. Li, “Enhancement of thermal conductivity of kerosene based Fe3O4 nanofluids prepared via phase-transfer method,” Colloids and Surfaces A: Physicochemical and Engineering Aspects, vol. 355, no. 1, pp. 109–113, 2010. View Article
[20] T. Edwards, “Kerosene fuels for aerospace propulsion composition and properties,” AIAA Paper, vol. 3874, 2002. View Article
[21] H. Brinkman, “The viscosity of concentrated suspensions and solutions,” The Journal of Chemical Physics, vol. 20, no. 4, pp. 571-571, 1952. View Article
[22] Y. Xuan and W. Roetzel, “Conceptions for heat transfer correlation of nanofluids,” International Journal of heat and Mass transfer, vol. 43, no. 19, pp. 3701-3707, 2000. View Article
[23] M. Levin and M. Miller, “Maxwell a treatise on electricity and magnetism,” Uspekhi Fizicheskikh Nauk, vol. 135, no. 3, pp. 425-440, 1981.
[24] K. Parekh and H. S. Lee, “Magnetic field induced enhancement in thermal conductivity of magnetite nanofluid,” Journal of Applied Physics, vol. 107, no. 9, p. 09A310, 2010. View Article
[25] A. Bejan and A. D. Kraus, Heat transfer handbook, vol. 1. John Wiley & Sons, 2003. View Article

