Journal of Fluid Flow, Heat and Mass Transfer (JFFHMT)

ISSN: 2368-6111

1. Introduction

Ampacity, a term for amperage capacity, is a measure of the current carrying capability of a wire or a collection of wires in a bundle.  Current practice relies on the use of published standards (e.g., [1]) to derate, both, single wires and bundles.  However, use of the standards is limited as none of the publicly-available standards provide a procedure to determine the unmargined maximum current on a conductor  within a bundle (for use in protective setting sizing), nor do they allow for mixed wire sizes, different wire jacket emittances, or a variety of currents on individual conductors.  Pursuit of an analytical approach is highly desirable to allow assessment of real world configurations not readily addressed by conditions assumed in the standards.

For a single wire under steady state conditions, the resulting conductor temperature is readily calculated by establishing a heat balance, i.e., the rate at which is heat generated within the wire due to ohmic heating must be equal to the rate at which it is rejected from the wire.  For a sufficiently long wire, heat losses through the end terminations may be neglected and the heat leaving the wire is by convection and radiation from the wire insulation jacket.  For wire bundles, characterization of the heat transfer is complicated due to the presence of multiple heat generating wires and interface conductances, radiation, and even gas conduction between adjacent wires.  Various studies have been performed by [2] and [3].  The complexities introduced with the bundle configuration result in a more tortuous heat transfer path from wires deep within the bundle to the free surface where heat is rejected from the bundle. Heat transfer considerations for wire-to-wire heat transfer within a bundle are presented.  The capability to model wire bundles has been extended from the methodology presented in [4] in the form of a complex wire bundle thermal model builder.  In this work, the model builder has been used to formulate three analytical configurations for use in comparison with a published derating standard.

2. Thermal Modeling

2.1. Wire to Wire Heat Transfer within Wire Bundles

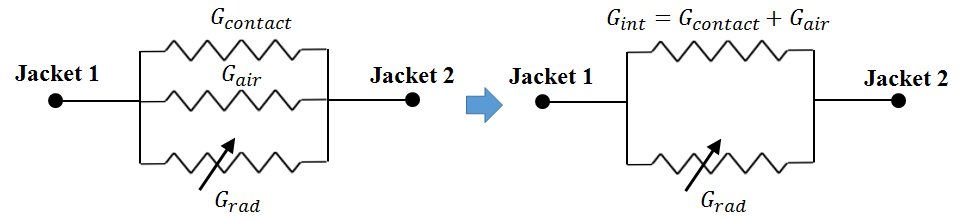
Reference [4] provided the derivation of the thermal network representing heat transfer within a wire bundle and noted wire-to-wire heat transfer between adjacent wire insulation jackets consisted of both radiative and conductive heat transfer paths.  Heat transfer between adjacent wires can occur due to direct contact between adjacent insulation jackets, via radiation, and also via air conduction in the gaps between wires for cases where an atmosphere is present.  A typical thermal network between wire jackets for two adjacent wires is shown in Figure 1. While the radiation conductance between adjacent wire jackets can be expressed as a fixed value, bench testing has suggested that the overall interface conductance , is a function of both temperature and pressure. Thermal radiation conductance , contact conductance (), and air conductance are discussed in the following sections.

2.1.1. Radiation Heat Transfer between Adjacent Wire Jackets

The general form of radiation heat transfer between two objects, is given by:

where the radiation conductance, , is the emittance of wire 1;  is the radiation interchange factor between wire jackets 1 and 2; is the Stefan-Boltzmann constant; and is the surface area of wire jacket 1.

Implementation of wire jacket-to-wire jacket radiation within the thermal model assumed the following:

1. Only first order radiation heat transfer was considered (i.e., direct radiation heat transfer between adjacent wire jackets with no reflection off of other wire jackets in view of the two wires of interest);
2. Both wire jackets were assumed to have the same infrared emittance;
3. Diffuse radiation heat transfer.

Under these assumptions, values were calculated for the range of possible wire size combinations (using the Cullimore and Ring Technologies, Inc. RadCAD^® application) by modeling adjacent wire jackets as infinite cylinders and normalizing the results based on radius ratios (Figure 2).

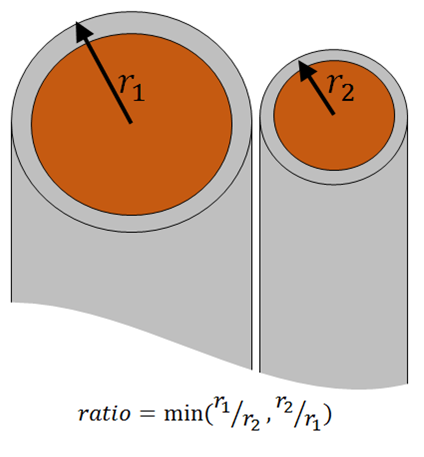
Results were formatted into a spreadsheet look-up table across the range of expected radius ratios and emittances.  When a wire bundle analysis configuration is changed, updating of the matrix (i.e., the interchange factor between wires i and j) is required.  For each pair of wires, the radius ratio is calculated and then a look-up of the corresponding value is performed based on the wire jacket emittance.  When the radius ratio exceeds that for which data is calculated, reciprocity is used, namely:

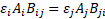
where, again,  and  are the emittances and wire jacket surface areas, respectively, for wires i or j. The radiation conductance between two adjacent wire jackets,  is:

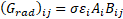
2.1.2. Variation of Contact Conductance with Wire Bundle Temperature

The remaining heat transfer paths are linear in nature (i.e., heat transfer from one jacket to another is linear function of ).  The heat transfer paths comprising , specifically,  and  may be considered to be in parallel with one another.  Between two insulation jackets the aggregate interface conductance is given by:

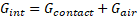
Heat transfer paths between three adjacent wire jackets are depicted in Figure 3.

Bench testing of wire bundles over a range of background currents for both in-air and vacuum conditions provided opportunities to correlate the thermal model for a large bundle comprised of approximately one hundred wires with a mixture of ethylene tetrafluoroethylene (ETFE) jacketed, 20 American Wire Gauge (AWG) and 22 AWG sizes.  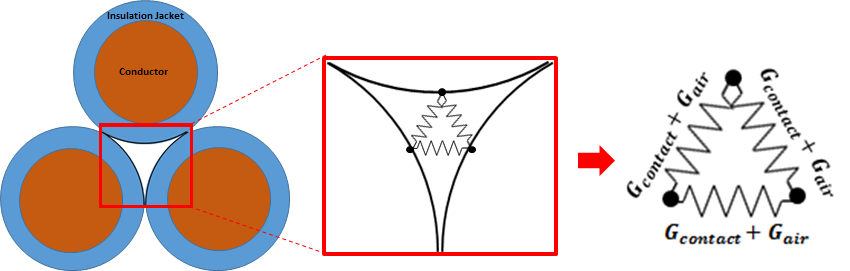By varying the wire background current a correlation between the wire bundle bulk average temperature and interface conductance was found by changing the interface conductance in the thermal model based on the calculated bundle bulk average temperature by trial and error.  A curve fit to the interface conductance data for the in-air analysis cases was performed and showed excellent correlation with a parabola (), the shape of which is depicted in Figure 4.

Once established, the equation was used to generate for bundle bulk average temperatures up to 200 ℃.  These data became the interface conductance values used in the thermal model over the use range of 20 ℃ to 200℃.

It was hypothesized that the interface conductance increase with the bundle bulk average temperature could be due to the thermal expansion of conductors and their jackets within the bundle.  As wire bundles are constrained on their exterior by an external jacket and/or cable ties, an increase in the bundle bulk average temperature could result in higher contact normal forces between adjacent wire jackets.  It is reasoned that even local heating within a bundle will result in expansion of the affected conductors and jackets resulting in a global effect across the bundle since the bundle is externally constrained.  As a demonstration of this mechanism, a thermal-stress model was formulated based on the following assumptions:

1. Copper and the ETFE jacket expand with temperature in accordance with published coefficient of thermal expansion (CTE) data. 
2. The bundle exterior radius was constrained to simulate the effect of an outer jacket and/or tie wrap.
3. Average temperature in the bundle was assumed constant for the analysis.

To test the hypothesis, a 19-wire bundle thermal stress model was built using MSC Patran^®, imported into MSC Mentat^® 2015, and solved using MSC Marc^® 2015.  Marc^® is a nonlinear finite element solver.  CTE data for, both, ETFE and copper were obtained from [5] and [6], respectively.  A quarter symmetry finite element model was developed in order to take advantage of the inherit dual symmetry.

The outer bundle perimeter was constrained from expansion to simulate the presence of an outer jacket or tie wrap.  The outer three elements represent the ETFE insulation jacket.  The inner three or more elements beyond the ETFE represent the copper wire.  The elements used are Quad 4 elements.  The model was comprised of 2,270 nodes and 1,368 elements with 702 elements for the conductors and 666 elements for the insulation jackets.

The ETFE insulation assumed a Young’s modulus value of 1.52 GPa, a density of 1700 kg/m³, and a thermal expansion coefficient of 4.11×10^-5 °C^-1 .  The copper conductor assumed a Young’s modulus of 117.2 GPa, a density of 8940 kg/m³, and a thermal expansion coefficient of 5.06×10^-6 °C^-1.  The 2-D model was constrained on the nodes on the leftmost boundary for translation in the x- and on the bottom nodes for y-displacement.  The constraints along with the starting temperature were the initial conditions.  The bulk temperature was increased from 20°C to 200°C across 10 equal increments of 18°C.  The model was run using the fixed adaptive/constant time step option. 

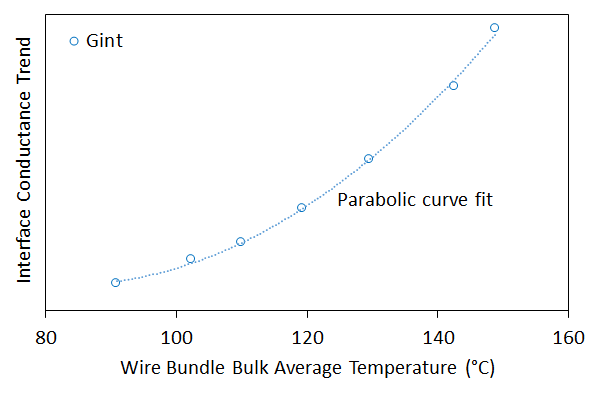
Normal contact force, assumed to be zero at 20℃, was recovered from the model over the temperature range of 20 ℃ to 200℃.  The calculated contact normal force for 200℃ the case is presented in Figure 5.  Both, linear and parabolic fits to the normal contact force versus bundle bulk average temperature curve yielded excellent fits with  and , respectively.  As the analysis showed, as bundle bulk average temperature increases, so too does the normal contact force which supports the hypothesis that contact conductance between adjacent wire jackets may be due to increasing normal contact force induced by temperature rise in the constrained bundle.  Figure 5 depicts a normalized contact normal force plot which shows higher forces between wires (yellow and orange elements) when compared to the lower contact forces (red and purple elements), signifying the forces between the wire bundle perimeter and wire insulation.

2.1.3. Air Conductance at Ambient Pressure

Correlation of the wire bundle thermal models at ambient pressure required adjustment of the wire jacket-to-wire jacket interface conductance which was shown to be a function of bundle bulk average temperature in the previous section.  In the presence of gravity, air will rise as it is warmed due to buoyancy driven forces.  However, if the region in which the air is contained is small, there is insufficient space for convection to develop and the resulting heat transfer occurs via gas conduction.  To determine whether air conduction or buoyancy driven convection is the driving heat transfer mode, the Rayleigh number, Ra is calculated by:

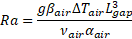
where  is the acceleration due to gravity,  is the air volume coefficient of expansion,  is the temperature difference across the air gap,  is the characteristic dimension of the interstitial region between wires, is the kinematic viscosity for air, and is the thermal diffusivity of air.

When , convection is possible.  For a gap between three 22 AWG wires (shown in Figure 6) and an assumed air temperature of 80 °C and air properties from [7],  and it is concluded that heat transfer is via air conduction.

A finite element approximation of the air gap formed by three adjacent wire jackets was used to estimate the effect of air conduction between wires.  In the model, the leftmost boundary of the air region is heated while the other two boundaries were held at a constant boundary temperature of 80 °C.  Steady state analysis was performed using Thermal Desktop^® and the Systems Improved Numerical Differencing Analyzer (SINDA), both by Cullimore and Ring Technologies, Inc. and temperature distributions at the left hand boundary are shown on the right hand side of Figure 6.

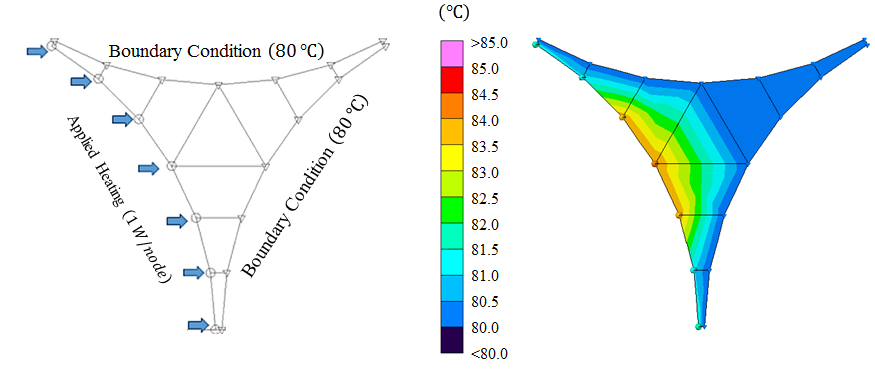
As can be seen from the steady state analysis results, temperatures on the heated wire jacket range from 81.13 °C to 84.04 °C.  A representative average temperature is 82.5 °C resulting in a .  For this air conduction analysis, it is noted that the heat transfer between the heated wire and the adjacent two wires is approximated by Fourier’s Law (i.e., ).  With a single heated wire and two parallel conduction paths, the equation becomes:

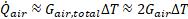
For the case analyzed, .

When comparing aggregate interface conductance for the air and vacuum cases, the difference between the two values is representative of the heat transfer contribution of air conduction.  At 80 °C, the difference between the air and vacuum cases was determined to be on the order of 1 W/℃ which is in general agreement with the calculation.

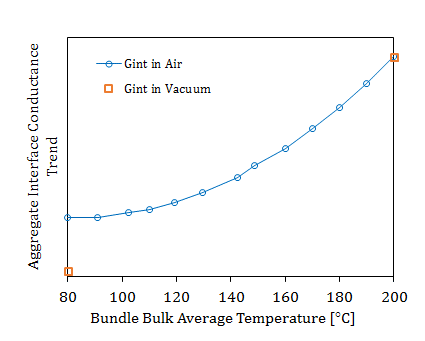
2.1.4. Aggregate Interface Conductance

Analysis in the preceding sections showed that heat transfer between adjacent wire jackets within a bundle varies with both temperature and the presence of air.  The effects were combined to form interpolation arrays used in the thermal model depending on whether an in-air or in-vacuum case is analyzed and is shown in Figure 7.  The blue curve represents the array of data used for correlation of the in-air cases whereas the orange squares represent correlation values derived from the in-vacuum test data.  Note that no curve was drawn between the orange data points as only two test points were available for correlation.  However, it is expected that any curve connecting the two vacuum points will lie on or below the blue curve due to the absence of air conduction between wire jackets in the vacuum case.  At high temperatures, the best correlation was found assuming the same vacuum conductance as the in-air case suggesting that at higher temperatures, contact conductance becomes the predominant heat transfer mechanism.

2.2. Complex Wire Bundle Thermal Model Builder

The Complex Wire Bundle Thermal Model Builder was developed due to the aforementioned limitations of the bundle spreadsheet model discussed in [4].  Specifically, due to Microsoft Excel^® matrix inversion limitations, a maximum of 50 wire bundle elements could be modeled.  Additionally, for vacuum analyses, the convergence of the temperature solution algorithm was not achieved for very low external bundle emittances.

The Complex Wire Bundle Thermal Model Builder also uses Microsoft Excel^® but only as a “front end” allowing users to specify wire bundles comprised of up to 150 elements where an element may be a wire, a sub-bundle jacket or an outer jacket.  When a user specifies a wire, the model building logic creates a wire conductor as well as an insulation jacket for each wire specified.  Users may specify current values for each individual wire, wire gauge, jacket type, proximity to adjacent wires within the bundle, external environment (air or vacuum) and environment temperature.  The tool uses Microsoft Excel^® functions and Microsoft Visual Basic^® routines to create an equivalent thermal network model in the Cullimore and Ring Technologies, Inc. Systems Improved Numerical Differencing Analyzer (SINDA) format.

2.3. Comparison of Wire Bundle Analytical Models with a Derating Standard

In order to determine the feasibility of applying wire bundle thermal models as a tool for bundle derating, three wire bundle models were analyzed and compared with [1].  Wire bundles comprised of seven, nineteen, and thirty-seven 22 AWG wires, depicted in Figure 8, were modeled using the Complex Wire Bundle Thermal Model Builder and SINDA input files were generated.  Minor edits were made to the SINDA files to allow for user adjustment for bundle external jacket emittance, wire resistance per unit length and wire current.

The selected bundle sizes allowed comparison to the derating procedure over a reasonable range of bundle sizes.  Additionally, the selected bundle sizes afforded a symmetry to aid the modeling process whereby each configuration had a single, centrally-located conductor which resulted in the highest predicted temperature.

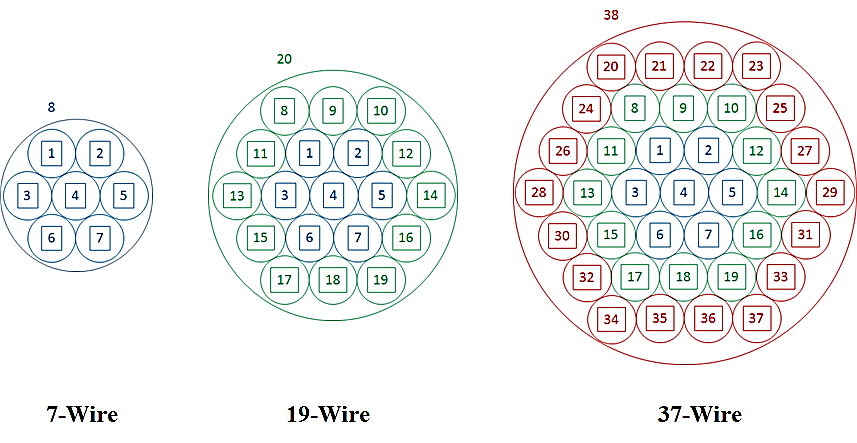
Steady state analysis was performed to determine the background current required in each wire that would result in a predicted central conductor temperature of 200 ℃.  The derating procedure in [1] was applied to determine ampacity for similarly sized bundles assuming a 100 percent loaded bundle in air at atmospheric pressure at 20 ℃.  Two analysis cases were studied for each bundle size.  The first case assumed the measured resistance per unit length, whereas the second case assumed the maximum allowable  per the wire specification (e.g., [8]).  For both cases, a high emittance external bundle jacket () was assumed to demonstrate the difference between what is allowed per the specification and the potential gain by using a measured value.  A comparison of the results is presented in Table 1.

Table 1. Comparison of model-predicted maximum allowable current with derating procedure.

	Maximum Current per Wire to Attain 200 °C on Hottest Wire (A)
Configuration	Model Prediction Meas. , High	Model Prediction Spec. , High	SAE 50881 F (Section 6.7) [1]
7 Wire	10.26	10.00	9.68
19 Wire	7.54	7.18	6.34
37 Wire	6.12	5.90	4.71

It is important to note that while the model builder has produced models that have been correlated to test data, the analysis discussed here has not been corroborated with test data and is only meant to serve as a comparison with a published derating standard.  Future work will aim to obtain such data.  However, it is noted that the standard produces a conservative result when compared to the model.

It should also be noted that different standards may rely on different assumptions.  At the very least, some assumptions are not stated or are vague and would benefit from clarification.  A history of wire derating standards is given in [9] and notes a safety factor for individual wires but changes in wire construction have made the applicability of the originally assumed safety factor less clear.  This makes a direct comparison between the model predictions and the standard impossible until additional test data are obtained.

3. Conclusion

Improvements to existing wire bundle thermal models for ampacity determination have been presented.  Components of wire jacket-to-wire jacket heat transfer consist of direct contact conductance, thermal radiation, and, for in-air cases, air conduction.  The heat transfer mechanisms have been implemented in a Complex Wire Bundle Thermal Model Builder.  A large bundle model was correlated to test data resulting in data to correlate the wire jacket-to-wire jacket heat transfer.  The wire jacket-to-wire jacket contact conductance is observed to be a function of the wire bundle bulk average temperature.  It is hypothesized that thermal expansion of the wire jackets within a constrained bundle leads to increased contact normal force between adjacent wire jackets and, hence, increased contact conductance and has been supported with finite element analysis.  Subsequently, three bundles of various sizes were modeled and compared to a derating standard with encouraging results.  Additional test data should be pursued and correlated to corresponding models to determine the potential for wider applicability of analysis as a tool for wire bundle derating.

References