Journal of Fluid Flow, Heat and Mass Transfer (JFFHMT)

ISSN: 2368-6111

1. Introduction

Nearly a fifth of the UK’s final energy consumption in 2015 was used for heating applications in the domestic sector, using gas boilers as the heat source [1]. In order to decarbonize this sector, the use of heat pumps is an option being considered; however, their use should when possible be restricted to off peak times to prevent an increase in the peak electrical grid demand [2].

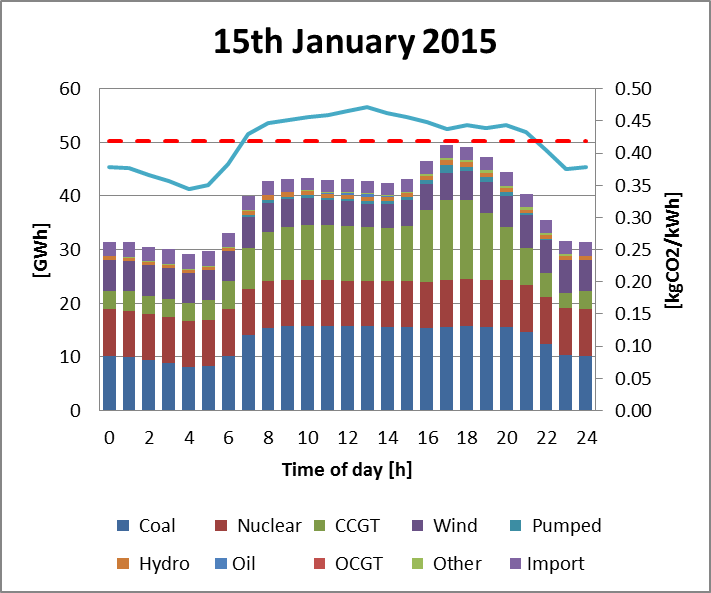
Figure 1 presents the composition of electricity generation by source supplied to the UK national grid on the 15^th January 2015. The CO₂ emissions associated with this profile were calculated based on the emission coefficients obtained by Hawkes et al. [3].

To effectively decarbonize this sector, heat pump CO₂ emissions should be less than that of the currently used conventional gas burning domestic heating systems (around 204 gCO₂/kWh_th [3], [4]); and their usage should the restricted to off peak electrical load times to minimise both carbon intensity and peak load.

To meet these requirements, heat pumps are usually operated using either the economy 10 or economy 7 tariffs [4], with hot water buffer tanks used to offset the electrical load and meet the heat demand required.

Hot water buffer tanks have a constant heat capacity over their working temperature range from 40 to 65°C when used for conventional space heating [5], hence requiring a considerable volume to meet 8h of space heating load.

Encapsulated phase change materials (PCMs) with a phase transition temperature between 50 and 60 °C can effectively increase the storage capacity of common hot water cylinders for the required temperature range, hence reducing the buffer tank water volume, allowing more heat to be stored for a given volume.

Known organic PCMs melting in this temperature range are the Paraffin waxes (RT54HC [6]) and fatty acids, as the eutectic mixture studied by Baran et al. [7]. Other known candidate PCMs are salt hydrates, but their high subcooling usually prevents them from working within a narrow temperature range.

The eutectic mixture of magnesium nitrate hexahydrate with magnesium chloride hexahydrate along with the other 2 organic candidates discussed, were characterized experimentally using differential scanning calorimetry.

The heat capacity thermograms of each PCM, presented in Figure 2, were experimentally determined using a TA instruments Discovery differential scanning calorimeter [8] with a temperature ramp rate of (1°C/min).

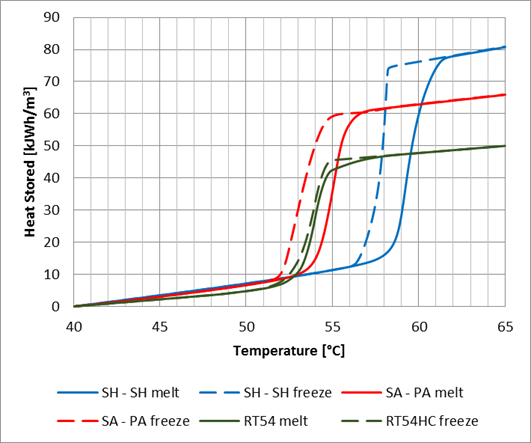
Table 1 presents a comparison between the three selected PCMs , from which it can be seen that the salt hydrate eutectic mixture is nearly 3 times more energy dense than water, within the 40 to 65˚C temperature range.

Table 1. Properties of  PCMs selected for potential use in space heating applications.

PCM	Temperature Range		H stored	H/ HH2O	λ	Price
	T min (°C)	T max (°C)	kWh/ m3		W/ m.K	£/ m3	£/ kWh
41%MgCl2.(H2O)6 + 59%Mg(NO3)2.(H2O)6(SH-SH)	40	65	81	2.81	0.600	99	1.21
36% stearic acid + 64% palmitic acid (SA-SPA) [7]			67	2.29	0.260	351	5.24
RT 54HC [6]			50	1.74	0.200	800	15.72

2. Numerical Model Developed

A 2D finite volume model was developed in Matlab to simulate a packed bed latent heat energy storage system, with macro-encapsulated PCM spheres. In the numerical model it was assumed isotropic heat propagation among the PCM, varying density, heat capacity and thermal conductivity with temperature to account phase change.

Charge and discharge of the container was simulated by passing a fluid flowing through the packed bed, exchanging heat by convection with the spheres.

The Heat Transfer Flow (HTF) Reynolds number was calculated using equation (1), based on the void fraction between the spheres within the container (φ), and the flow length specified to be half of a sphere’s cross sectional perimeter. The convective heat transfer coefficient was determined using the method detailed by Wakao et al. [9], where the average Nusselt Number, expressed in eq. (2), is the product of the form factor (fa), calculated according to eq. (3) for a packed bed with spheres of the same size and the laminar and turbulent Nusselt numbers,  for a packed bed, equations (4) and (5), calculated according to Gnielinski et al. [10].

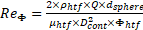
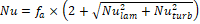
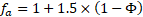
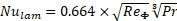
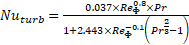
The numerical algorithm used required formulation and solution of both mass and transport matrices at each time step to solve the transient problem. Equation (6) presents the three set of equations used to compute the solution during each time step ([Γ1] the transport matrix, [C] the mass matrix, f is a variable (range from 0 to 1) that can be used to tune the algorithm from an explicit to an implicit approach (all models were solved implicitly, f=1). The term {F_out} accounts for the inlet mass flow.

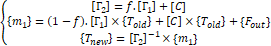
The packed bed in the simulation consisted of a specified number of horizontal layers each having a set number of spheres, illustrated in Figure 3 A. The spheres in each layer were considered to behave in the same way with identical temperatures the model thus required that equations were solved for a single sphere per row, as illustrated in Figure 3 B and C.

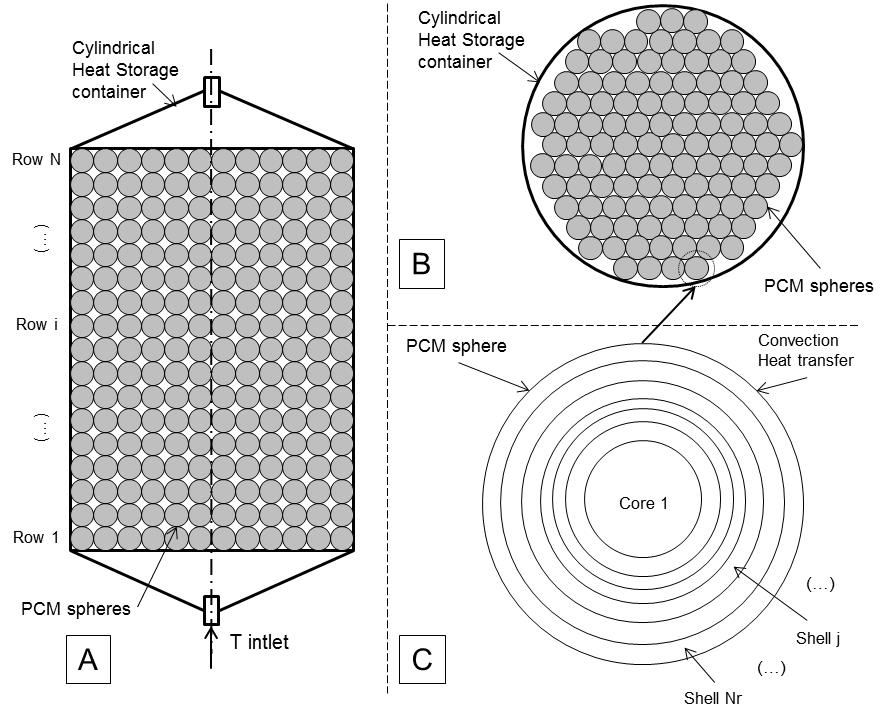
The model employed backward spatial discretization for the mass flow in the HTF, and unidirectional radial heat transfer within the sphere, illustrated schematically in.

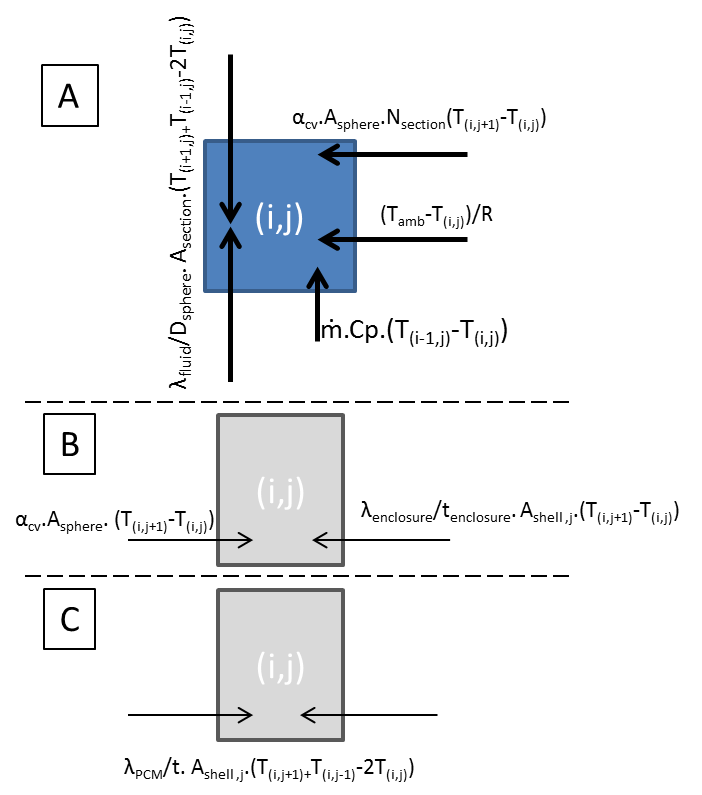
The container’s heat loss to ambient represented by the thermal resistance coefficient (R) in Figure 4 (A), assumed an ambient temperature of 20 °C and a convective heat transfer coefficient of 5 W/m².K.

The convergence criteria applied in each time step was achieved by setting the mass flow coefficients to zero and the convective coefficients to a Nusselt of 1 in the transport matrix, simulating a zero flow rate. Then based on the temperature residuals between iterations, the algorithm was looped until the absolute cumulative difference for all spheres was below 10^-5 °C.

2.1. Model Verification

Tanvir et al. [11] studied a packed bed with 770 capsules containing the PCM sodium nitrate [12]. The latent heat store was charged and discharged with air 20 °C above and below the PCM melting point respectively. A schematic of their rig configuration is presented in Figure 5. The system could store a total of 1.05 kWh_th between 286°C and 326°C. Air heaters were used to maintain the charge and discharge temperatures at the required levels. The system performance was recorded measuring is transient temperature evolution in 4 rows of thermocouples spaced 50.8 and 203.2 mm from the bottom of the tube. In the numerical model developed, they were named row 1 and 4 respectively.

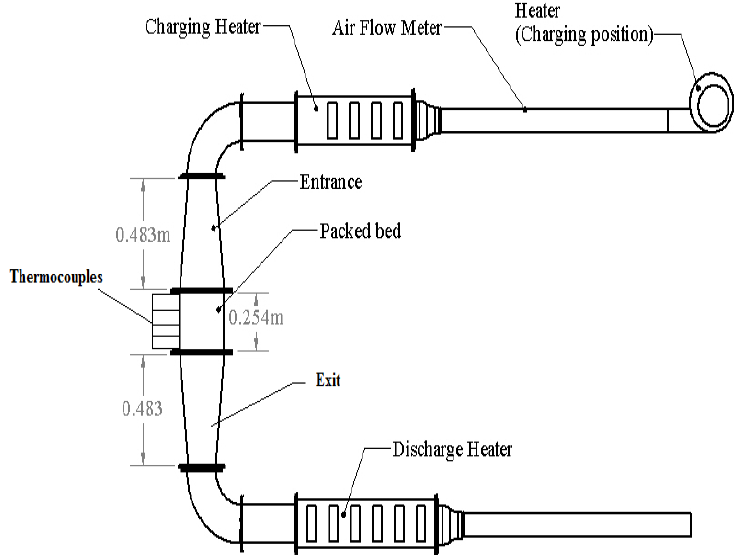
The packed bed store was formed from a 254mm length of a 10” carbon steel tube insulated with flexible insulation 152mm thick. The key system properties are presented in Table 2.

Table 2. Store dimensions and heat transfer fluid flow properties for the experiments performed  by Tanvir et al. [11].

Bed height [mm]	254
Bed Diameter [mm]	254
Total Volume of packed bed [L]	12.87
Bed Porosity	0.35
Insulation thickness [mm]	152
λ insulation [W/m.K]	0.1
HTF:
Flow rate [m3/s]	0.0419
Reynolds Number (Re)	1293 - 1171
Prandlt (Number)	0.77
Nusselt Number (Nu)	52.3 – 49.6
Convection HT coefficient (hcv) [W/m2.K]	86 - 87

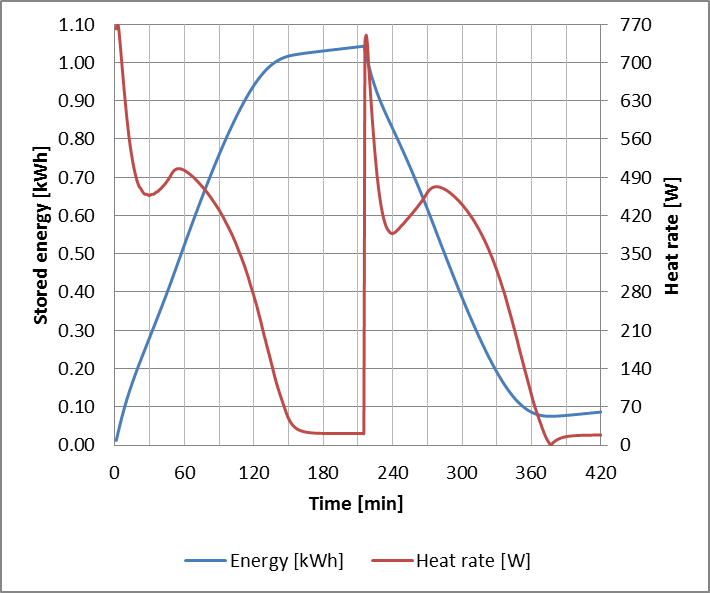
The model predictions and the experimental results are presented in Figure 6. The predictions from the developed model are in good agreement with both the experimentally measured air and PCM temperature profiles. The abrupt temperature changes at 0 and 225 minutes are due to the higher initial temperature differential between HTF inlet and the store, leading to surge in the container’s heat rate, as it can be seen in Figure 7.

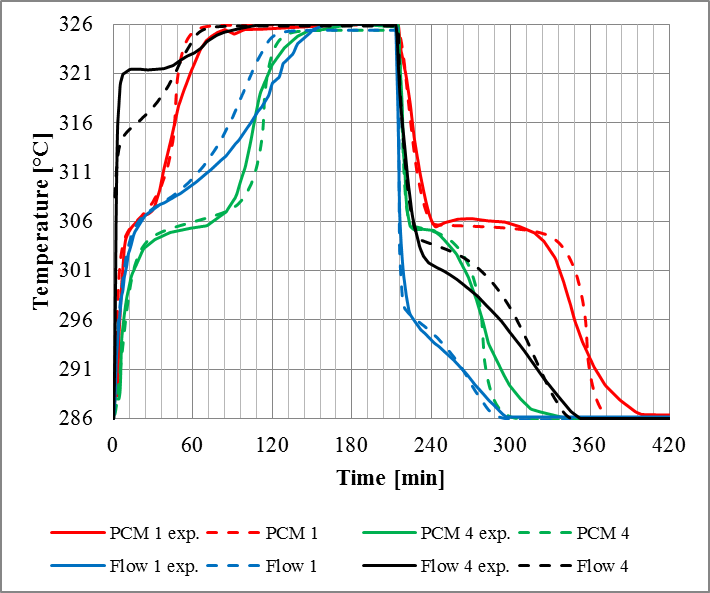
The slight discrepancies observed during both charging and discharging processes may be due to some geometrical irregularities from the experimental packed bed resulting from the molten PCM, leading to an uneven air flow spread among the packed bed of spheres [11].

The predicted values for power input/output and stored energy are presented in Figure 7. Of the 1.05 kWh_th transferred to the store, only 0.98 kWh_th were effectively discharged, losing 0.07 kWh_th through heat losses to ambient.

2.2. System Design and Integration

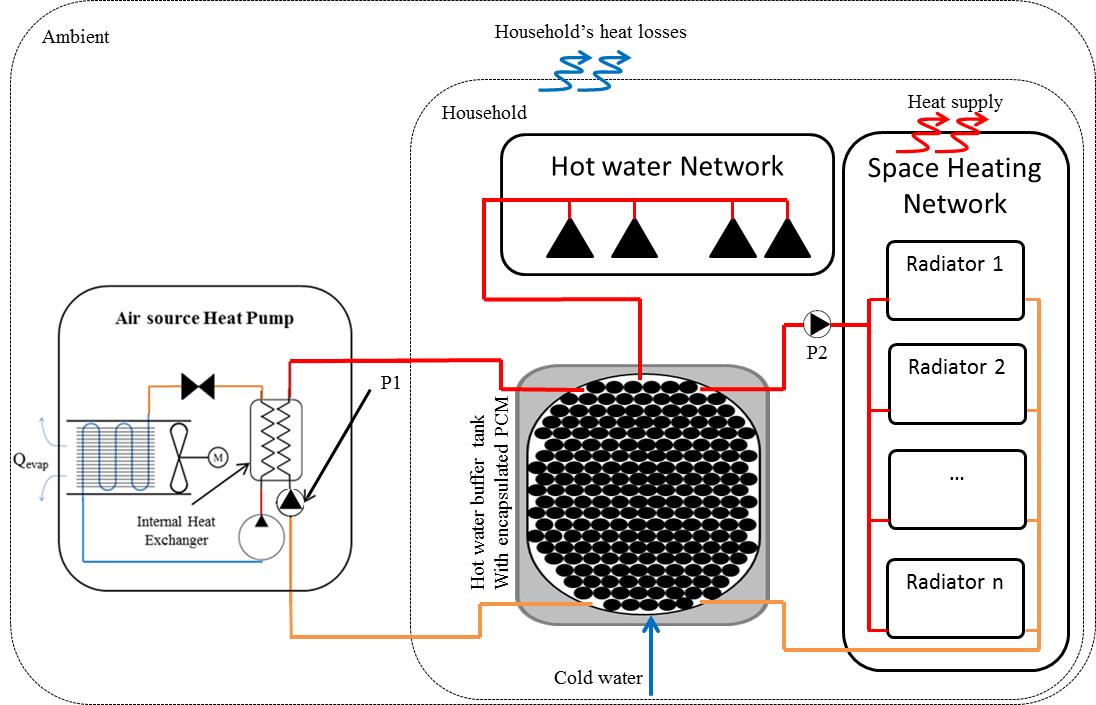
Following a numerical optimization, the optimized latent heat store was integrated in a domestic heating system, illustrated schematically in Figure 8. For the simulation the store was charged during off peak hours, based on  economy 10 electricity tariffs [4], using the characteristics of Daikin Altherma V high temperature air source heat pump [13].

The latent heat store was sized to meet the highest 8 hour heat demand for a typical semi-detached dwelling during a winter day. The building fabric thermal performance was considered to have been improved by insulation retrofit. The reason of selecting these type of household is due to its importance, since it represents around 6 million dwellings, more than a quarter of the UK’s housing stock in 2014, based on the English housing survey report made by the Department for Communities and Local Government [14].

The building properties employed are displayed in Table 3, were those used in an high-resolution stochastic integrated thermal and electrical domestic demand model developed by Mckenna et al. [15], [16].

Table 3. Dwelling properties used to predict system performance.

Space Heating Demand	32.86	kWh
DHW demand	5.62
Latent heat storage capacity	16.85
Avg U per floor area	1.273	W/m2.K
Household’s internal capacitance	530.7	kJ/K
Floor area	87	m2
Set temp.	20	°C
Emitters total water volume	42.03	l
Emitters total surface area	20.54	m2

Daily carbon emissions associated with the heating system were calculated using the grid CO₂ emissions presented in Figure 1. To determine the heat pump’s coefficient of performance (COP), Daikin Altherma V technical data sheets [17] were used, with a 65 °C outlet temperature assumed, including also the effect of defrost cycles.

Circulating pump (P2) transferred heat from the latent heat storage to the household heat distribution system, assuming a water flowrate of 6 l/min and circulating pump (P1) transferred heat from the heat pump to charge the store, with a maximum flow of 30 l/min varying according to the household needs and store capacity, as shown schematically in Figure 8. Pump (P2) controlled the inside air temperature band of 19.5/20.5°C from 07.00 to 23.00 and 15.5/16.5°C in the remaining hours. Figure 9 presents the balance equations for the 2 extra nodes added to simulate the house central heating system.

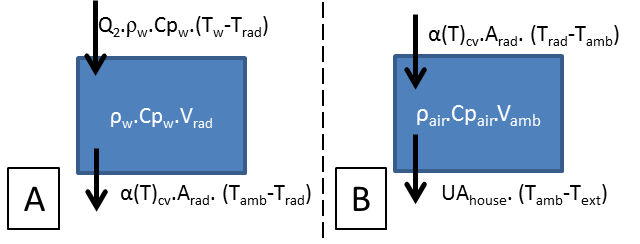
The convective heat transfer coefficient of the heat emitters was determined during each time step by calculating the Rayleigh number using the instantaneous emitter-ambient temperature difference, considering a typical emitter height of 600m and the emitters to be connected in parallel to the circulation loop.

The highest household’s heat demand was measured from 05.00to 13.00, being 14.61 kWh_th.

After a market research, common hot water buffer tanks have 450mm diameter, varying their height according to the required capacity. A 300L buffer tank was chosen having 430 PCM spheres with a 90mm diameter, then compared to similar storage capacity using only water. Table 4 presents the geometrical properties of the modelled packed bed and hot water stores. The volumetric ratio for the spheres was determined from the trend line studied by Mueller et al. [18]; having the latent heat store a ratio of container to sphere diameter of 5.

Table 4. Buffer tanks geometrical properties and heat transfer characteristics.

Parameter	LHS	DHW Tank
Number of spheres	430	-
Sphere OD [mm]	90	-
Sphere wall thickness [mm]	1	-
Container diameter [mm]	450	558
Container height [mm]	1890	2345
H/D ratio	4.2
Container volume [L]	301	574
PCM volume [L]	153	-
PCM store fraction [%]	51	-
Heat transfer area [m2]	10.942	-
Specific HT area [m2/m3]	36	-
To water buffer tank [kWh/kWh]	1.91	1
Flow Reynolds Number (12 l/min)	176-262	-
HTF hcv [W/m2.K]	204-225	-
Container heat storage capacity between 40 and 65⁰C [kWh]	16.50
PCM heat storage capacity [kWh]	12.39	-
Water + encapsulant heat storage capacity [kWh]	4.11	16.50
Overcapacity [%]	12.93
λ Insulation [W/m/K]	0.035
t insulation [mm]	50

With the eutectic mixture of magnesium nitrate hexahydrate and magnesium chloride hexahydrate (specs detailed in Table 1), occupying 51% of the container volume, its thermal energy storage capacity nearly doubled compared to the same stored volume using only water, between 40 and 65°C, due to the increased heat capacity of the PCM between 56 and 62 °C, as shown in Figure 2.

Table 4 presents also the general heat transfer characteristics of the latent heat stores. The packed bed latent heat store has a laminar fluid flow regime, having higher convective heat transfer coefficients due to the enhanced flow mixing provided by the PCM spheres.

For comparison purposes, both had the same height to diameter ratio of 4.2 and the same overcapacity.

3. Results Discussion

Figure 10 presents the predictions of heat supplied for the semi-detached dwelling in a winter day using McKenna’s high resolution stochastic model [16]. In these simulations, there is significant variance in the household’s internal temperature around the set point, varying from 14.2 to 24.6 °C, consequence of having wider boiler set point temperatures.

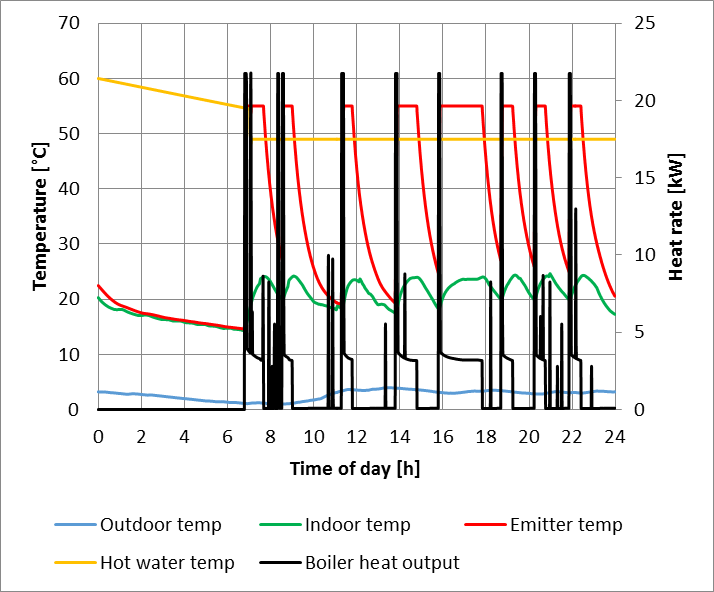
The predicted temperatures and heat supply rates from simulations using the developed Matlab model for the latent heat store are presented in Figure 11 and for the hot water buffer tank in Figure 12.

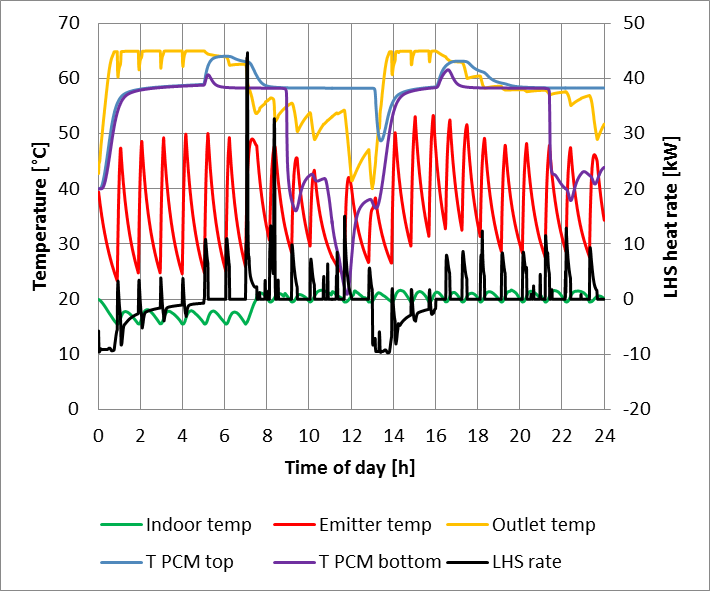
The model predicted more frequent indoor temperature variations due to the narrow temperature control band (+-1°C). This operating mode can easily be achieved by using the circulating pump in off peak hours transferring the stored heat to the household’s space heating system.

The predictions show that the PCM’s higher thermal capacity around 60°C, allows the latent heat store to provide heat for two 8h periods (from 05.00 to 13.00 and from 16.00 to 24.00) of hot water, successfully offsetting the heat pump operation to economy 10 low tariff periods. The latent heat store had longer charging times; due to the slow heat propagation among the PCM spheres.

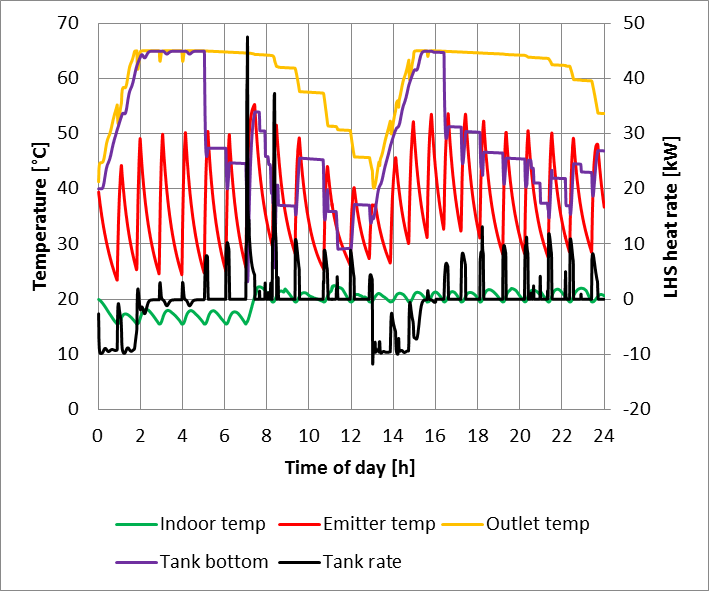
In the end of the 1^st discharge period (around 12.00), both stores were fully discharged, requiring the latent heat store an extra heat of 579Wh and the hot water tank and extra heat of 534Wh, due to the high heat demands from space heating and hot water combined.

The predicted reduction in carbon emissions based on the current grid emission values [1], [3] for the heat pump systems with the latent heat store was 11%, and nearly negligible (2%) for the hot water tank; compared to the conventional boiler system. That is due to the important role that the PCM spheres have enhancing thermal stratification, allowing the packed bed tank to reach the required temperature at its top faster.

4. Conclusions

Thermal stores including phase change materials have the potential to store larger amounts of thermal energy within smaller temperature ranges compared to stores just using water. Due to the low thermal conductivity of many PCMs, poor rates of thermal diffusion within the PCM can reduce significantly the nominal storage system charge and discharge heat transfer rates.

Due to the versatility in store geometry possible with encapsulated packed bed systems they appear to be a feasible option for integrating PCMs into conventional domestic space heating systems. Inserting the PCM filled spheres into standard water buffer tanks can be achieved without major technical challenges.  The lower PCM volume fraction achievable when compared to more compact store designs such as the tube in tube, can limit the increase in heat storage capacity.

The numerical model developed to evaluate the replacement of conventional gas fired boilers with heat pumps coupled with a PCM thermal store to offset heat pump operation from peak electrical demand periods, predicted that CO₂ emissions could be reduced by 11% for the improved semi-detached dwelling studied using current grid emission values, being that reduction negligible when inserted a bigger hot water tank instead. That reduction applied to the 6 million semi-detached dwellings in the UK would result in an overall reduction of 1.68 million tonnes of CO₂ yearly.

To meet the UK’s 80% carbon emissions reduction targets by 2050, the electrification of current water heating systems must be decarbonized. Increased decarbonisation of the UK electrical grid will have more impact if the domestic heating sector is electrified. The increased peak electrical load generated by electrification of heat can therefore be moderated by using buffer tanks with their thermal capacity increased by including encapsulated PCMs to allow the operation of heat pumps to be time shifted to periods of low grid electrical load while still meeting heat demand and comfort requirements.

Acknowledgements

The research presented in this paper is funded by the EPSRC through grant [EP/K011847/1], the Interdisciplinary centre for Storage, Transformation and Upgrading of Thermal Energy (i-STUTE) and Loughborough University.

References