Volume 3 - Year 2016 - Pages 92-98
DOI: 10.11159/jffhmt.2016.011
Theory and Indirect Measurements of the Drag Force Acting On a Rising Ellipsoidal Bubble
Abdullah A. Kendoush1, Kim W. Gaines2, Carrie W. White2
1Department of Nuclear Engineering Technology
2Department of Electrical & Computer Engineering Technology
akendoush@augustatech.edu, kgaines@augustatech.edu, cwcarriewild@gmail.com
Augusta Technical College
Augusta, Georgia, USA
Abstract - A series of experiments were performed to obtain the drag force and rise characteristics of oblate ellipsoidal bubbles (OEB) in tap water at room temperature. The experiment utilized a 1.219m tall Plexiglas column with square cross section of 15.24cm sides designed and constructed for this purpose. Photographs captured the bubbles as they rose and grew vertically in the water column, and were analysed to determine the bubble radius. The drag force and velocity of rise were determined indirectly. An equation (CD=2.667/Fr) was derived for the drag coefficient of the OEB where Fr is the Froude number. The experimental results validated this equation and earlier work by Reference [8]. The merit of this work is in the capability of the bubble's semi-major and semi-minor axes measurement being used to determine the drag coefficient and mean rising velocity of bubbles. Results were compared favourably with the current and published theoretical results.
Keywords: Ellipsoidal bubble, Two-phase flow, Drag coefficient, Froude number.
© Copyright 2016 Authors - This is an Open Access article published under the Creative Commons Attribution License terms Creative Commons Attribution License terms. Unrestricted use, distribution, and reproduction in any medium are permitted, provided the original work is properly cited.
Date Received: 2016-12-05
Date Accepted: 2016-10-24
Date Published: 2016-12-13
Nomenclature
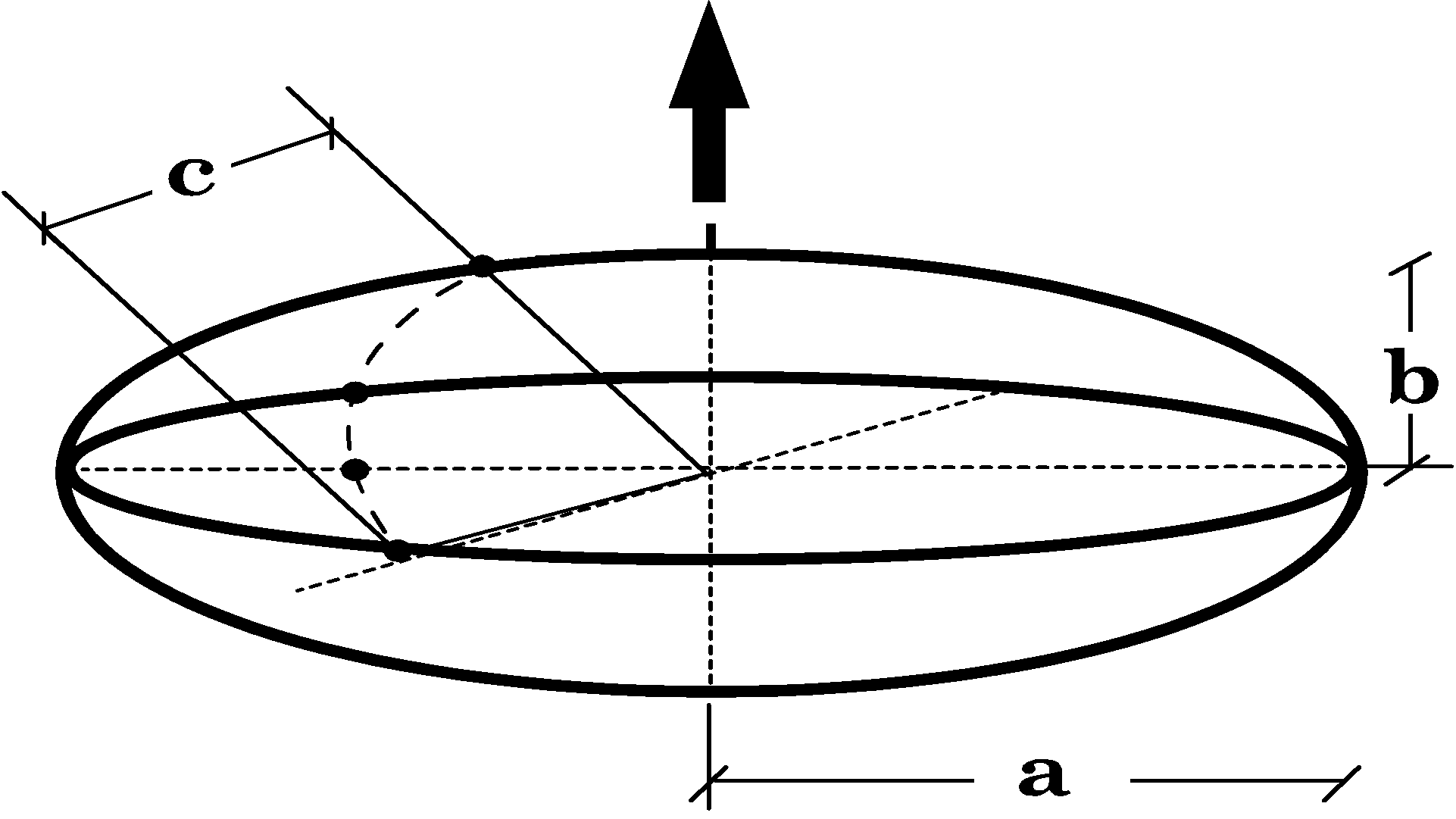
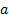 : semi-major axis of the OEB
: semi-major axis of the OEB- b: semi-minor axis of the OEB
- c: semi-depth axis of the OEB
- B: buoyancy force
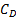 : drag coefficient
: drag coefficient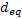 : equivalent diameter of the OEB
: equivalent diameter of the OEB- D: drag force
- Eo: Eötvös number (
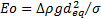 )
)  : Froude number (
: Froude number ( for OEB) and (
for OEB) and (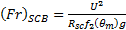 for SCB)
for SCB)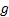 : acceleration due to gravity
: acceleration due to gravity- M: Morton number (
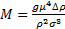 )
) - OEB: oblate ellipsoidal bubble
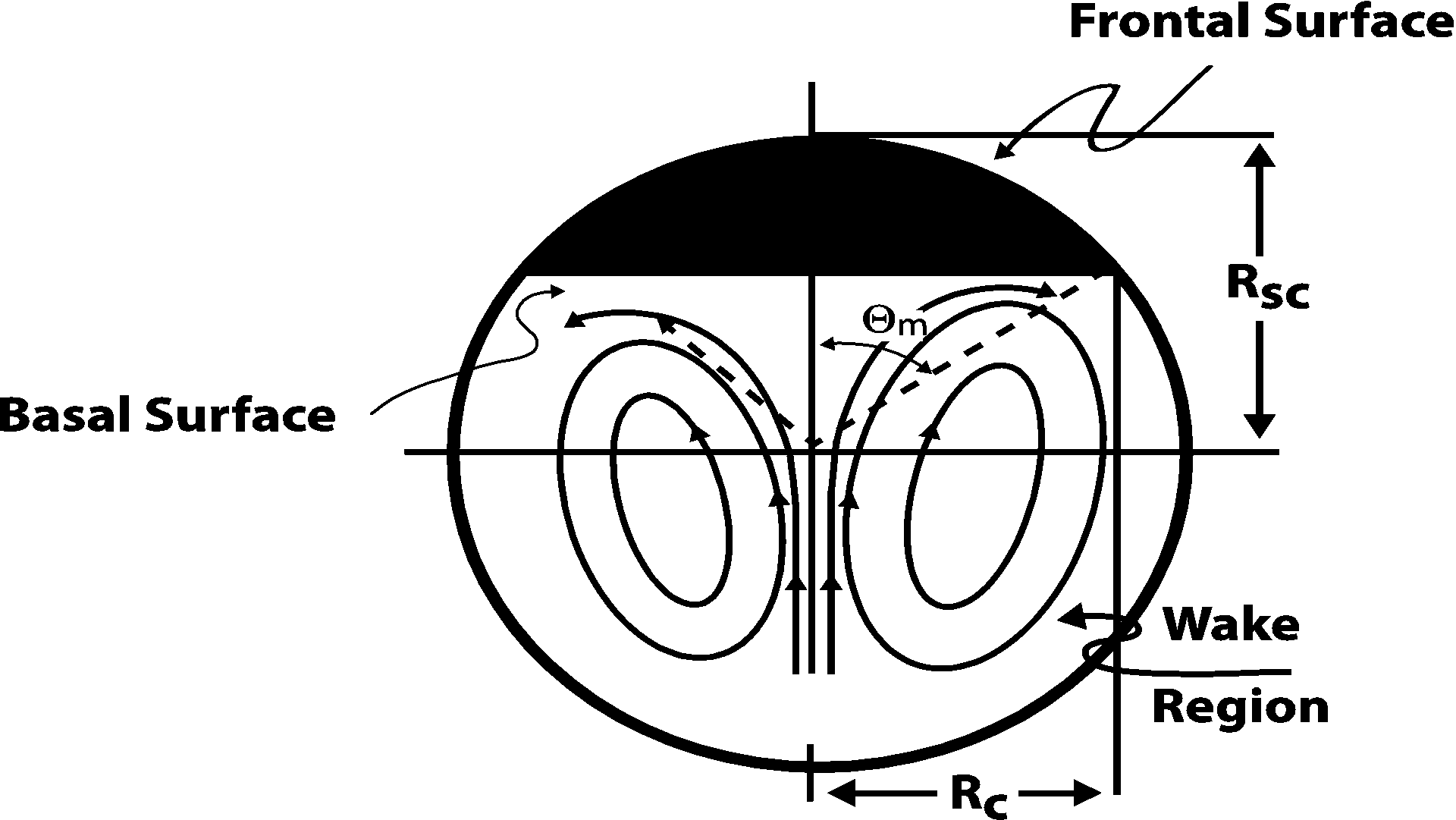
- Rc: basal radius of SCB
- Re: Reynolds number (Re=
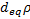 U/
U/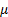 )
) 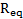 : equivalent radius
: equivalent radius- Rsc: radius of curvature of the SCB
- SCB: spherical-cap bubble
- U: velocity of the OEB
- We: Weber number (We=2
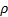 U2/
U2/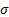 )
) - x: aspect ratio of the OEB
- V: volume of the OEB
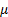 : absolute
viscosity
: absolute
viscosity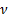 : kinematic
viscosity
: kinematic
viscosity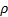 : density
of liquid
: density
of liquid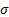 : surface
tension
: surface
tension
1. Introduction
There are three main stages of bubble shape development during rise in an extended liquid: spherical, ellipsoidal, and spherical-cap (SCB). The main industrial applications of bubble dynamics are found in nuclear power generation, chemical industry, oil transportation, heating, ventilation, and air conditioning, and mineral processing.
Moore
[1] analysed the motion of the OEB and obtained an equation for the variation
of the drag coefficient with respect to the aspect ratio of the OEB and
Reynolds number (Re=Udeq/![]() ) where U is the bubble
velocity, deq is the equivalent diameter, and
) where U is the bubble
velocity, deq is the equivalent diameter, and ![]() is
the kinematic viscosity of the liquid.
is
the kinematic viscosity of the liquid.
Meiron [2] solved for the distortion of the OEB from its spherical shape as the
bubble velocity increased using potential flow theory. He predicted a
functional relationship between Weber number(We=2![]() U2/
U2/![]() )
where σ is the surface tension and aspect ratio
)
where σ is the surface tension and aspect ratio ![]() (Fig.
1).
(Fig.
1).
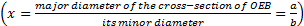
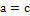 ).
).On the experimental front, Wu and Gharib [3] concluded from their experiments that the OEB acquired a spiral path and became unstable when the bubble equivalent diameter exceeded 0.15cm or the aspect ratio exceeded 1.6. Talaia [4] performed a similar experiment to ours but used air-water system and air- glycerol system as an additional testing liquid. He acknowledged the viscosity-independence rise of a large bubble but did not make a clear distinction between the OEB and the SCB.
Wenyuan et al. [5] performed similar experiments to ours, but they used non-Newtonian aqueous solutions of polyacrylamide (PAM) and carboxymethylcellulose (CMC). Only in CMC aqueous solutions, bubbles shapes look oblate ellipsoidal similar to the ones we observed and recorded. PAM aqueous solutions produced some peculiar shaped bubbles. Aoyama et al. [6] studied the shapes of OEB's rising in infinite stagnant liquids and produced an empirical correlation for the bubble aspect ratio as a function of Eötvös and Reynolds numbers. Their definition of the aspect ratio is the reciprocal of ours. The work of Veldhuis et al.[7] revealed the existence of wakes behind the rising OEB's by using Schliern optics. They found a correspondence between these wakes and the spiraling motion of the OEB.
It appears from the literature survey that no information was provided for the experimental measurements of the drag coefficient of OEB. The main objective of this experiment was to demonstrate the possibility of measuring the dimensions of the OEB to determine its velocity and drag coefficient. In addition, some validation of previous theoretical work, by the first author, was attempted.
2. Theory
2.1. The Drag on the OEB
The drag coefficient of the OEB is defined as follows
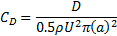
The drag force D in this equation was obtained by calculating the buoyancy force B acting on the OEB as these two forces oppose each other during the rise of the OEB under steady state conditions. Omitting the weight of the bubble, the buoyancy force B becomes
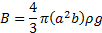
where ![]() is the density
of the liquid and
is the density
of the liquid and ![]() is the
acceleration due to gravity. Substituting this equation in Eq. (1) and B=D,
yields the following
is the
acceleration due to gravity. Substituting this equation in Eq. (1) and B=D,
yields the following
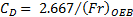
Here ![]() is the Froude number that compares the inertial
forces to the gravitational forces acting on the bubble. This equation shows
the viscous effects and the presence of surfactants do not play a significant
role on the drag particularly at high Re numbers. Ellingsen and Risso
[14] arrived at similar equation but with different parameters. This specific Fr
number was chosen to be based on the minor axis "b" because it is
considered as the main axis responsible for the symmetry of the bubble. This
specific Fr number is a more sensitive indicator of the oblateness of
the bubble, than that based on the equivalent diameter normally employed by
other authors.
is the Froude number that compares the inertial
forces to the gravitational forces acting on the bubble. This equation shows
the viscous effects and the presence of surfactants do not play a significant
role on the drag particularly at high Re numbers. Ellingsen and Risso
[14] arrived at similar equation but with different parameters. This specific Fr
number was chosen to be based on the minor axis "b" because it is
considered as the main axis responsible for the symmetry of the bubble. This
specific Fr number is a more sensitive indicator of the oblateness of
the bubble, than that based on the equivalent diameter normally employed by
other authors.
To make the
drag coefficient based on the equivalent radius, we used ![]() .
.
2.2. The Drag on the SCB
The following proof is to check the validity of the drag dependence on the Fr
number. We analyzed the case of the steady rise of the SCB. For Re >
100, the drag coefficient data approaches ![]() , a value obtained by many authors
(e.g., [9, 10]).
, a value obtained by many authors
(e.g., [9, 10]).
The volume of the SCB (Fig. 2) is as follows [11]
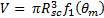
where ![]() is the wake angle, and
is the wake angle, and ![]() =
=![]() .
.
The
wake angle ![]() of the SCB lies within the range of
(45 - 56) degrees [12, 13]). Assuming that an average wake angle of 52 degrees
was considered, Eq. (4) becomes the following
of the SCB lies within the range of
(45 - 56) degrees [12, 13]). Assuming that an average wake angle of 52 degrees
was considered, Eq. (4) becomes the following
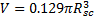
It
should be noted that the factor 0.129 in this equation has a range of 0.077-
0.166 based on the choice of ![]() with the average value of
with the average value of ![]() . The volume
of an equivalent sphere corresponding to the above volume is as follows
. The volume
of an equivalent sphere corresponding to the above volume is as follows
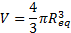
Equating Eq. (4) and (5) yields,
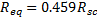
From
the idealized geometry of the SCB (Fig. 3), we have ![]()
This radius is useful in calculating the drag coefficient as it provides for the projected area as shown below
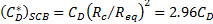
where ![]() is the drag coefficient of the SCB
based on equivalent radius, and
is the drag coefficient of the SCB
based on equivalent radius, and ![]() is the equivalent
radius of the equivalent spherical volume of the SCB. Setting the drag force
equal to buoyancy, the following is derived
is the equivalent
radius of the equivalent spherical volume of the SCB. Setting the drag force
equal to buoyancy, the following is derived
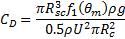
Through further simplification of this equation,
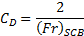
where
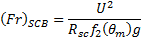
and
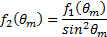
Davis and Taylor [18] found in their work that
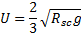
Substituting Eq. (13) into Eq. (10) yields
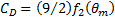
As
far as the authors are aware, this new equation for the drag coefficient of the
SCB was not reported before. Further, the equation needs consideration for
future validation work. This is a powerful equation that determines the drag
from a single measurement of the wake angle. For ![]() 52 degrees, this equation becomes
52 degrees, this equation becomes
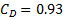
Substituting this equation into Eq. (8), yields
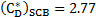
This is the same equation of Wegener and Parlange [9] mentioned earlier. Thus, we proved that the new Fr number-dependent drag coefficients of Eq. (3) have some kind of validity.
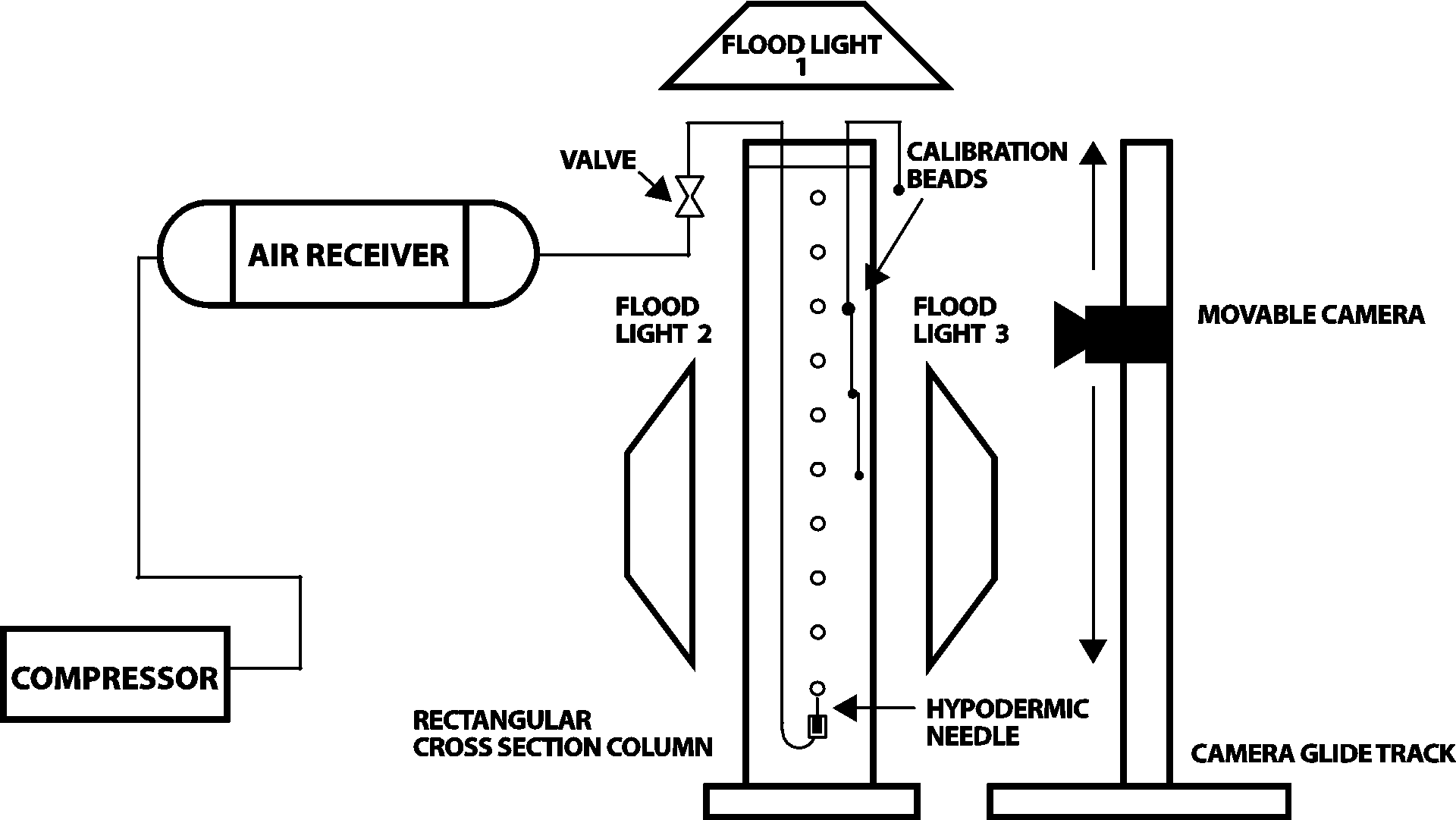
3. Apparatus and Procedure
The experiments were carried out in a Plexiglas column with a 1.219m height and a cross-section of 15.2x15.2 cm (Fig. 3). The column was filled with tap water at 20 oC at atmospheric pressure.
Air was introduced into the column via an air compressor, a pressure regulated air receiver, clear vinyl tubing, and a manually operated valve. The clear tube was fitted with a glass cane-shaped appendage. The cane-shaped glass ensured the bubble would rise in the middle of the tank. A 1cc syringe with an inside needle diameter of 0.1397mm was used to introduce air bubbles into the column through a hand controlled valve. Illumination for the experiment was achieved using flood lights. A Canon camera 60D, with a Tamron SP 24-70MM F/2.8 Di VC USD lens was used with an image resolution of 0.084 x 0.081 mm/pixel (5184 x 3456 effective pixel size). The camera with a 7 fps (frames/second) rate was manually moved to ensure the bubble remained in the center of the frame of reference throughout its rise. Calibration of bubble size was accomplished via three solid spherical beads with diameters of 4.978 ±0.001mm, 3.3937±0.0001mm, and 2.972±0.001mm respectively. The beads were lowered into the rectangular column with clear fishing string. The typical distance on which the bubble was filmed was (20-30cm). No attempt was made to measure the rising speed of the camera. The camera was moved manually following the rise of the OEB bubble. The following equivalent sphere diameter was used in the processing of the data
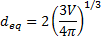
where ![]() is the volume of the OEB that is
given by
is the volume of the OEB that is
given by
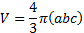
and ![]() is
the semi-major axis, b is the semi-minor axis, and c is the semi
depth axis ( Fig. 1). The photographs produced a two-dimensional image with
measurable
is
the semi-major axis, b is the semi-minor axis, and c is the semi
depth axis ( Fig. 1). The photographs produced a two-dimensional image with
measurable ![]() and
b axes. The length c was assumed to be equal to the semi-major
axis; therefore, Eq. (18) becomes
and
b axes. The length c was assumed to be equal to the semi-major
axis; therefore, Eq. (18) becomes
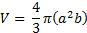
The OEB bubble velocity was not measured directly, but calculated using the following [12]
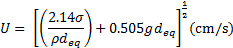
![]() in this equation was measured and
used to calculate bubble velocity. The water properties were listed in Table 1.
When the bubble detaches from the needle, its shape is spherical (
in this equation was measured and
used to calculate bubble velocity. The water properties were listed in Table 1.
When the bubble detaches from the needle, its shape is spherical (![]() =1).
As the bubble rises in the column, its shape flattens, gradually becomes OEB
and its motion becomes oscillatory.
=1).
As the bubble rises in the column, its shape flattens, gradually becomes OEB
and its motion becomes oscillatory.
Figure
4 shows the flow regime map of the three main bubble shapes (i.e. spherical,
ellipsoidal, and spherical cap) as given by Clift et al. [12]. Based on
calculating Re number, Morton number (![]() ), and Eötvös number (
), and Eötvös number (![]() ), our experimental results fall
within the OEB region (filled dots). This region was characterized by Clift et
al. [9] as a wobbling OEB. Our results were concerned with the mean rising
motion and deformation of the bubble.
), our experimental results fall
within the OEB region (filled dots). This region was characterized by Clift et
al. [9] as a wobbling OEB. Our results were concerned with the mean rising
motion and deformation of the bubble.
Our
range of Re number was 506 - 979, M = 2.569 x ![]() , and the range of
, and the range of ![]() was 0.415 - 2.41.
was 0.415 - 2.41.
Figure 5 shows a typical photograph of the rising OEB in water with the hanging calibration beads.
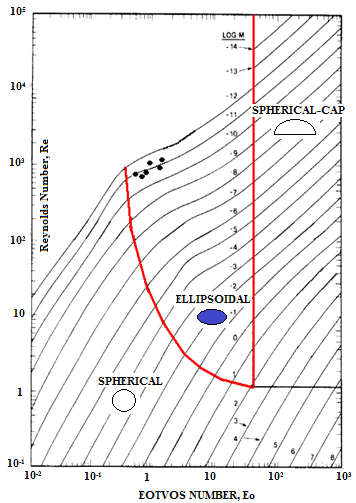
Table 1. Water properties at 20 ̊C.
| Density kg/m3 | Surface Tension N/m | Kinematic viscosity m2/s |
| 998.2 | 72.74*10-3 | 1.0034*10-6 |
4. Results and Discussion
We followed the experimental evidence of Ellingsen and Risso [14] who proved the influence of surfactant of the tap water was negligible on the bubble motion. This, in addition to the derived Eq. (3), motivated us to use Eq. (20) in the present calculations of the bubble velocity, despite the fact that the equation was supposed to be applied to a clean system. The bubble emerges from the tip of the needle via a hand-regulated valve. It starts rising in spherical form, and then it changes to ellipsoidal.
Figure
6 A, B, and C show favourable comparisons between the present experimental data
(particularly Fig. 6B and C) and the theoretical results of Kendoush [8], Moore
[1], and Blanco and Magnuadet [15]. There is a discrepancy at ![]() =1.5
of Fig. 6A between theory and experimental data. This can be attributed to
the closeness of
=1.5
of Fig. 6A between theory and experimental data. This can be attributed to
the closeness of ![]() =1.5
to bubble sphericity. Bubble motion in this region is rectilinear and Ellingsen
and Risso [14] indicated that the rectilinear trajectory is unstable. However,
Kendoush's [8] theory seems to be closer to the experimental data than both
Moore [1] and Blanco and Magnuadet [15]. It should be noted that the values of
the aspect ratio
=1.5
to bubble sphericity. Bubble motion in this region is rectilinear and Ellingsen
and Risso [14] indicated that the rectilinear trajectory is unstable. However,
Kendoush's [8] theory seems to be closer to the experimental data than both
Moore [1] and Blanco and Magnuadet [15]. It should be noted that the values of
the aspect ratio ![]() was
obtained directly from the photographs of the OEB, hence the photographs
determined the values of
was
obtained directly from the photographs of the OEB, hence the photographs
determined the values of ![]() .
.
The
newly-derived Equation (3) indicates that the drag forces are independent of
viscous effects. For sufficiently high Reynolds number, the drag coefficient no
longer evolves with the Re number. Figure 7 shows a close agreement between the derived Eq. (3) and the experimental data. The
experimental data are based on the velocity of bubble rise obtained from Eq.
(20) and the measured bubble dimension b. These velocities and b
were used into ![]() to get
to get ![]() .
.

5. Uncertainty Analysis
To
find the uncertainty in the measured values of ![]() , we substitute Eq. (19) into (17) to
get the following after simplification
, we substitute Eq. (19) into (17) to
get the following after simplification
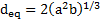
Call
the uncertainty in ![]()
![]() Uncertainty can be obtained by
applying the following equation (Holman [16])
Uncertainty can be obtained by
applying the following equation (Holman [16])
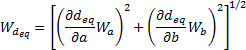
where
the uncertainty in measuring the parameter "![]() " is
" is ![]() = ± 0.01mm and the uncertainty in
measuring b is
= ± 0.01mm and the uncertainty in
measuring b is ![]() = ± 0.05 mm. Adding these errors to
those reported in §3, we get
= ± 0.05 mm. Adding these errors to
those reported in §3, we get ![]() mm and
mm and ![]() = ± 0.0952 mm. Partial
differentiating Eq. (21) and substituting in Eq. (22) yielded
= ± 0.0952 mm. Partial
differentiating Eq. (21) and substituting in Eq. (22) yielded ![]() = ± 1.665 mm or (21.16%).Suneetha
and Raghuram [17] measured the bubble diameter by using a high speed camera.
They reported 18% percentage error in their measurements. The same procedure
was done on Eq. (20) and yielded
= ± 1.665 mm or (21.16%).Suneetha
and Raghuram [17] measured the bubble diameter by using a high speed camera.
They reported 18% percentage error in their measurements. The same procedure
was done on Eq. (20) and yielded ![]() = ± 3.596 cm/s or 9.65 %. In
addition, using Eq. (3) yielded
= ± 3.596 cm/s or 9.65 %. In
addition, using Eq. (3) yielded ![]() = ± 0.0783 or 19.79 %.
= ± 0.0783 or 19.79 %.
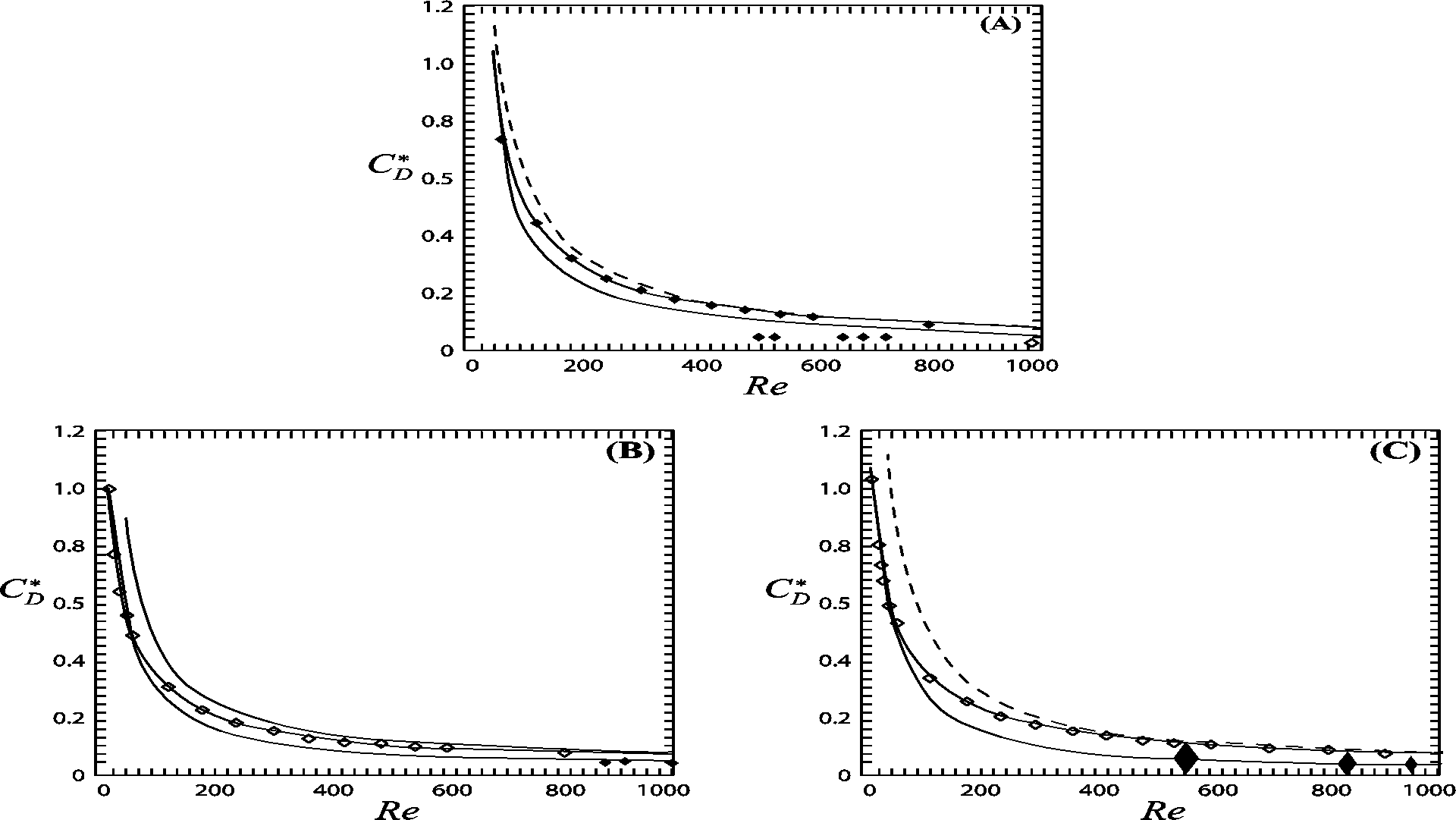
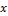 = 1.5, (B)
= 1.5, (B) 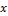 = 1.75, and (C)
= 1.75, and (C) 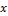 = 1.95.
= 1.95.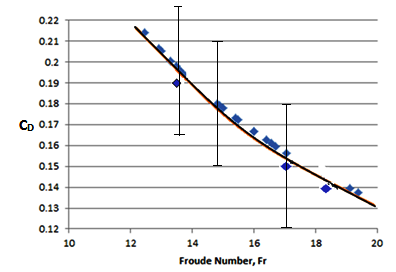
6. Conclusion
The present work dealt with experiments on isolated air bubbles of the oblate ellipsoidal shape. Oblate ellipsoidal bubble was rising in still water. Photographs of OEB's were captured and analysed, and the data were recorded. From the photographic data, we obtained information on bubble velocity and drag. The present experimental results validated the newly-derived drag Eq. (3). This study showed that the present results also validated earlier publication of Kendoush's [8] drag equations of the OEB at high oblateness values.
Future studies will include alternate fluids, thus varied Re numbers, and aspect ratio values.
Acknowledgements
Thanks to the Southern Nuclear Company, Mr. Stephen Schroeder, Mr. J. Michael Weiksner, Sr., Dr. David M. Maryniak, and Ms. Sherrie Rowe for their efforts and support.
References
[1] D. W. Moore, "The velocity of rise of distorted gas bubbles in a liquid of small viscosity," J. Fluid Mech., vol. 23, pp. 749-766, 1965. View Article
[2] D. I. Meiron, "On the stability of gas bubbles rising in an in viscid fluid," J. Fluid Mech., vol. 198, pp. 101-114, 1998. View Article
[3] M. Wu and M. Gharib, "Experimental studies on the shape and path of small air bubbles rising in clean water," Phys. Fluids, vol. 14, pp. L49- L52, 2002. View Article
[4] M. A. R. Talaia, "Terminal velocity of a bubble rise in a liquid column," Int. J. Mathematical, Computational, and Quantum Engineering, vol. 1, pp. 214-218, 2007. View Article
[5] F. Wenyuan, M. Youguang, J. Shaokun, Y. Ke and L. Huaizhi, "An experimental investigation for bubble rising in non-Newtonian fluids and empirical correlation of drag coefficient," ASME J. Fluids Engineering, vol. 132, pp. 021305-1 - 021305-7, 2010. View Article
[6] S. Aoyama, K. Hayashi, S. Hosokawa and A. Tomiyama, "Shapes of ellipsoidal bubbles in infinite stagnant liquids," Int. J. Multiphase Flow, vol. 79, pp. 23-30, 2016. View Article
[7] C. Veldhuis, A. Biesheuvel and L. Van Wijngaarden, "Shape oscillations on bubbles rising in clean and tap water," Phys. Fluid, vol. 20, p. 040705, 2008. View Article
[8] A. A. Kendoush, "Heat, mass, and momentum transfer to a rising ellipsoidal bubble," Ind. Eng. Chem. Res., vol. 46, pp. 9232-9237, 2007. View Article
[9] P. P. Weneger and J.-Y. Parlange, "Spherical-cap bubble," An. Rev. Fluid Mech., vol. 5, pp. 79- 100, 1973. View Article
[10] D. D. Joseph, "Rise velocity of a spherical-cap bubble," J. Fluid Mech., vol. 488, pp. 213-223, 2003. View Article
[11] A. A. Kendoush, "Theory of convective heat and mass transfer to spherical-cap bubbles," AIChE Journal, vol. 40, pp. 1440-1448, 1994. View Article
[12] R. Clift, J. R. Grace and M. E. Weber, Bubbles, drops, and Particles, New York: Academic Press, 1978. View Book
[13] J. R. Landel, C. Cossu and C. P. Caulfield, "Spherical-cap bubbles with a toroidal bubbly wake," Phys. Fluids, vol. 20, no. 12, pp. 122101-1-122101-3, 2008. View Article
[14] K. Ellingsen and F. Risso, "On the rise of an ellipsoidal bubble in water: oscillatory paths and liquid-induced velocity," J. Fluid Mech., vol. 440, pp. 235-249, 2001. View Article
[15] A. Blanco and J. Magnuadet, "The structure of the axisymmetric high-Reynolds number flow around an ellipsoidal bubble of fixed shape," Phys. Fluids, vol. 7, no. 6, pp. 1265-1274, 1995. View Article
[16] J. P. Holman, Experimental Methods for Engineers, New York: McGraw-Hill, Inc., 1989. View Book
[17] T. B. Suneetha and P. T. Raghuram, "Bubble size measurements and error analysis in a gas-liquid ejector," Indian J. Chemical Technology, vol. 19, pp. 442-446, 2012. View Article
[18] R. M. Davies and S. G. I. Taylor, "The mechanics of large bubbles rising through extended liquids in tubes," in Proc. Roy. Soc., London, 1950. View Article

