Journal of Fluid Flow, Heat and Mass Transfer (JFFHMT)

ISSN: 2368-6111

1. Introduction

Indirect contact drying is a unit operation in which the wet material to be dried is not in direct contact with the heating medium but separated by a conducting surface. One approach to model the behavior of this type of drying operation is through the use of the penetration model developed by Schlünder [2], which is based on fundamental physical principles. In its origin, the penetration model was developed to describe heat transfer from a hot surface to a solid bed of particles at rest occurring in two sequential stages [1]. In the first stage, heat is transferred from the heated surface to the first layer of particles adjacent to the surface, resulting in a contact resistance. In the second stage, heat is conducted progressively inside the bed of particles, causing a penetration resistance of the solid bed [2], [3], [4]. This concept was adapted to represent the indirect drying of solids, subjected to some mixing action, by introducing a geometrical parameter to include the random motion of the particles.

The penetration model has been used to describe the drying process under different operating conditions such as vacuum [1], [5] and in the presence of an inert gas atmosphere [6]. Tsotsas and Schlünder [7] have included the solid hygroscopic affinity to the model with the addition of an adsorption curve in the development of the model. They have studied the influence of the solid particle size distribution on the model prediction. Even though the penetration model was developed for the drying of a bed of solid particles resting on a heated horizontal flat surface, it was possible to use it to model the drying of a solid bed occurring in various types of dryers: moving discs, rotating cylinders equipped with lifters, fixed cylinders with rotating blades.

Intelvi [8] and Intelvi et al. [9] modelled the drying of pharmaceutical products in a rotating-disc batch dryer, under both vacuum and atmospheric pressure with very satisfactory results. They used discrete element method (DEM) model for their simulation and compared their results with the experimental results published by Schlünder and Mollekopf [1] where it was determined that the results were very well simulation except at very high RPM (> 45) and very low moisture content (< 0.1%) where the internal mass transfer resistance becomes non-negligible. Osman et al. [10] also used the DEM model where they added the heat transfer phenomena and obtained good results. Jorquera [11] and Vega [12] have applied the penetration model to describe the batch drying of different types of solids in a rotating-tube dryer, a much more complex geometry than disc dryers. They obtained results that were consistent with experimental data. Shene et al. [13] introduced the concept of continuous operation to the penetration model. This concept was subsequently implemented by Riquelme [14], who obtained very good results when compared with experimental results. Tsotsas et al. [15] proposed a new approach in order to identify the missing elements in the conventional penetration model, such as the mechanical and statistical properties of solid particles.

However, the penetration model has been mostly tested at the laboratory scale with dryer prototypes (discs, rotating drums and rotating drum with flights) of relatively low capacity, which raises the question on the predictive ability of the penetration model for the indirect drying of solids at an industrial-scale operation using rotary-tubes, rotating-coils and rotating-discs dryers. One research group has, however, extended the penetration theory to compute the drying kinetics of municipal sewage sludge [16][17].

The main objective of this paper is to model the continuous indirect drying of copper concentrate in a rotating-coil dryer at an industrial scale where steam condensing within the rotating coils serves as the heat source. This is in contrast with the applications reported in the literature where modeling and simulation are performed with prototypes of indirect dryers of low capacity most often operating in batch mode. In this paper, it is therefore desired to model and simulate the drying behavior of an industrial copper concentrate rotating-coil dryer using the penetration model of [1].

The main objective of this paper is to model the continuous indirect drying of copper concentrate in a rotating-coil dryer at an industrial scale where steam condensing within the rotating coils serves as the heat source. This is in contrast with the applications reported in the literature where modeling and simulation are performed with prototypes of indirect dryers of low capacity most often operating in batch mode. In this paper, it is therefore desired to model and simulate the drying behavior of an industrial copper concentrate rotating-coil dryer using the penetration model of [1].

2. Model Description

The penetration model of Schlünder and Mollekopf [1] was developed for indirect drying operation in a rotating disk dryer in which the heating surface had a circular geometry. The solid bed of particles is distributed over the surface of the heated disks where it absorbs heat such that the solid moisture eventually reaches the saturation temperature and the evaporation process begins. While the bed is static, the contact time between the hot disk surface and the solid particles is known and equal to the residence time. However, in order to improve heat transfer, the solid bed is agitated using a series of mixers. As a result, the time for which the solid is in direct contact with the heating medium is not known and, to include this mixing effect in the model, a geometric parameter known as the mixing number N_mix is used. The mixing number correlates the estimated time (t_R) during which the solid particles are in contact with the heating surface and the time constant or the inverse angular velocity of the stirring device (t_mix):

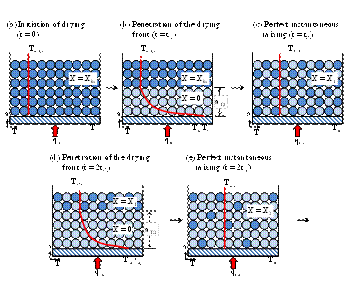
In this model (Figure 1), it is assumed that the stationary mixing process can be viewed as a sequence of unsteady mixing steps. Each step has a duration t_R which corresponds to an imaginary or fictitious time that the solid to be dried is in static contact with the heating surface (contact surface area between particles and heating surface for rotating disk dryers, rotary cylinder dryers equipped with lifters, cylindrical dryers with rotating blades or others).

At t = 0, the bed has an initial moisture content X_in and an initial temperature T_b,in. A drying front coming from the heating surface (a = 0) penetrates the bed to an arbitrary distance a_T,1. In the region between 0 < a < a_T,1, the solid particles are completely dry (X = 0) under the assumption that there is no bound moisture (non-hygroscopic bed), as schematically represented by the light color particles of Figure 1(b). In this zone, a temperature profile has developed and the bed properties can be approximated by treating the bed as a quasi-continuous medium. Beyond the moving drying front, for a > a_T,1, the solid particles are still at the same initial moisture content (X_in) and at a temperature T_b,in, as schematically represented by dark color particles of Figure 1(b). At the end of the static period (t = t_R), the bed is mixed instantaneously and perfectly. This step results in a uniform bed moisture X₁ and bed temperature T_b,1. This step marks the completion of the first period of contact and the initialisation of a second contact period. This process is repeated in the same manner until the bed of particles becomes completely dry. Figure 1 illustrates schematically the progressive drying of a bed of solid particles via the repeated drying-mixing cycles.

In this work, it is assumed that the control of the drying process depends solely on heat transfer and thus the mechanisms by which heat is transferred. In indirect dryers such as rotating discs, rotary cylindrical equipped with lifters, static rotary drum with rotating blades, rotating coils and others, it is possible to observe the presence of several heat transfer resistances. These resistances, going from the heating medium to the gaseous phase containing water vapor coming from the drying bed, are in series: (1) 1/h_vw is the resistance prevailing between the heating medium and the conductive wall (typically negligible compared to other resistances if the heating medium is steam), (2) 1/h_wall is the resistance due to conduction through the wall (negligible for metal wall), (3) 1/h_ws is the contact resistance between the heating wall and the solid bed of particles, (4) 1/h_sb is the resistance due to heat penetration into the bed of particles, (5) 1/h_p is the internal particle heat resistance (considered negligible for copper concentrate particles because of the small particle diameter of the order of tenths of microns, negligible porosity and high thermal conductivity) and (6) 1/h_vg is the resistance at the evaporation surface (considered negligible in this work). Even though there are several resistances in series, only two resistances are considered important: the contact resistance between the heating wall and the solid bed of particles and the penetration heat resistance of the solid bed [18].

The contact heat transfer coefficient (h_ws) can be estimated using the mathematical model developed by Mollekopf and Martin [19] while the bed penetration transfer coefficient (h_sb) is determined based on the properties of the particles for the dried bed. In addition, there are two mass transfer resistances: one for the bed permeation (1/β_sb) and another one for particle permeation (1/β_p). Studies have shown that the bed permeation resistance for static solid beds is very small and, for mixed solid beds, it is roughly zero such that it can be safely neglected [1]. The particle permeation resistance can also be neglected for non-porous particles, which is the case in this investigation for copper concentrate.

In summary, the penetration model proposes that the drying rate is a property of the solid bed instead of a property of the particles, which is the reason why the resistances due to solid particles are neglected. This is amply justified in this investigation due to the specific properties of copper concentrate particles. Therefore, the model proposed by Schlünder and Mollekopf [1] is used as a simplification of the real continuous drying process.

Performing an energy balance on a quasi-continuous medium with respect to the temperature gradient, the heat diffusion equation is obtained [20]:

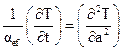
where α_ef represents the effective thermal diffusivity of the bed, defined as:

k_ef is the thermal conductivity of the bed, r_ef is the bed density and c_p.ef is the thermal capacity of the solid bed.

The initial and boundary conditions for the section of the bed in the vicinity of the heating surface can be defined as follows (Figure 1):
IC:    t < 0    T = T_b
BC1:   a = 0   T = T_h
BC2:   a = a_T T = T_b

By introducing these boundary conditions in Eq. (2), it is possible to describe the temperature profile of the bed at each instant within the time interval 0 < t < t_R:

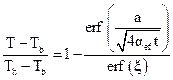
where ξ is the normalized drying front position, defined by:

The reduced drying front position can be estimated from the following expression [1]:

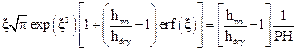
where PH is the phase change number that represents a measure of the intensity of the latent heat of vaporization compared to the sensitive heat. It is defined as:

An average individual heat transfer coefficient, h_sb,wet, for the penetration of the moist bed can be defined as:

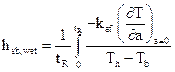
Evaluating  and substituting it in Eq. (8), the following equation is obtained for the average penetration heat transfer coefficient for the wet bed:

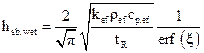
On the other hand, the individual heat transfer coefficient, h_sb,dry, for the penetration of the dry bed can be obtained from Eq. (9) because when the moisture content X tends to zero, ξ tends to infinity and erf ( ξ ) tends to unity giving rise to Eq. (10):

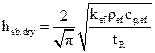
Combining the two individual heat transfer resistances in series (1/h_ws and 1/h_sb), it is possible to determine the overall heat transfer resistance to the flow of heat for both the dry bed (h_dry) and the wet bed (h_wet):

Knowing the overall heat transfer coefficient h_wet, it is possible to determine the heat flux both at the heating surface (a = 0) and the location of the drying front (a = a_T):

Assuming that the heat absorbed by the moisture at the drying front of the solid bed is only latent, that is the heat required to change the moisture from liquid to vapor without increasing the temperature, the rate of evaporation of the moisture from the bed can therefore be calculated as:

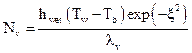
The change in the moisture content of the bed during the time period 0 < t < t_R is given by

where A_EFT is the total effective surface area for heat transfer (total contact surface between the solid particles and the heating surface) and M_SS is the total mass of the dry solid. Performing an energy balance on the bed, during the time period of the imaginary or fictitious static contact, the average increase in temperature of the bed (ΔT_b) can be determined by the following equation:

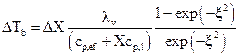
2.1. Model adaptation to a continuous drying operation

The penetration model was developed at the laboratory scale on batch dryers (rotating disks, rotary drum and fixed drum with rotating blades). For the modeling of a continuous indirect dryer such as rotary-coil dryers, it is assumed that all the particles move as a plug flow system with a uniform and constant speed throughout the dryer. Therefore, the axial movement during each imaginary or fictitious contact period t_R is the distance traveled by the particles along the length of the dryer. According to Shene et al. [13], this distance is given by:

where V_con represents the average velocity of the copper concentrate particles in the axial direction and is given by the following expression:

W_con is the mass flow rate of the dry concentrate within the dryer, ρ_ef is the effective density of the bed of dry concentrate and S_con is the cross sectional area of the flow of concentrate, which is obtained as a function of the internal geometry of the dryer and the solid holdup [21]. During the time period t_R, both the mass of solid and the effective heat transfer area () are given by the following expressions [14]:

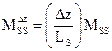
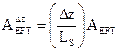
where L_S is the length of the dryer. Moreover, the residence time of the concentrate within the dryer can be calculated using an expression similar to Eq. (18).

It is also possible to relate the section of the dryer Dz calculated using Eq. (18) and the overall length of the dryer L_S:

where N_T is the number of sections of the dryer of length Dz that the concentrate travels during each time interval t_R, as discussed before. Likewise, a similar expression can be established between the residence time t_res and the imaginary od fictitious contact time t_R:

3. Materials and Methods

The rotary-coil dryer is enclosed in a fixed metal chamber. The bottom portion of the drying chamber is cylindrical whereas the top of the drying chamber has a rectangular shape. The coils, serving as the heat transfer surface, are mounted on a hollow central shaft and supplied with steam. The central shaft and the coils are attached to a drive unit which is rotated to provide mixing and heat transfer. Figure 2 gives the schematic diagram of the lateral and transversal cut-out views of the rotary-coil dryer showing the main components of the dryer.

The heating system consists of a central cylindrical rotor to which heating coils are attached. The heating coils consist of a series of concentric rings connected through tube manifolds as shown in Figure 3.

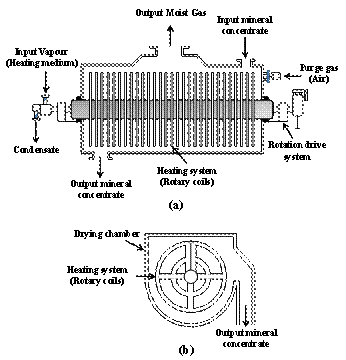
Steam is the heating medium and is supplied from a boiler to the central rotating shaft of the dryer and subsequently distributed to the surrounding coils. Due to the rotation of the heating system, the condensate produced when heat is transferred to the concentrate is withdrawn through the tube manifolds to the rotor and then recirculated to the boiler.

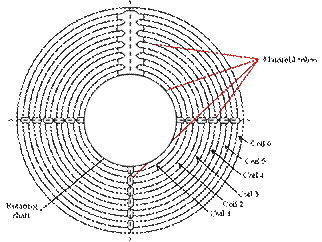
Table 1. Main dimensions of the industrial rotating-coil dryer.

Dimensions	Magnitude [units]
Length	8.480 [m]
Diameter (circular bottom section)	2.772 [m]
Height above shaft (rectangular section)	1.664 [m]
Total heat transfer surface area	460 [m2]
Total effective area for heat transfer	237 [m2]
Total heat transfer volume	16.2 [m3]
Internal volume of the dryer shell	64.7 [m3]

The concentrate inlet port of the dryer is located at one end of the dryer. The inlet port is equipped with a double-gate valve used to regulate the amount of moist concentrate entering and to prevent at the same time undesired air intake. The dry concentrate is discharged through an adjustable damper at the opposite end of the dryer which allows controlling the solid holdup within the dryer. Moisture that evaporates during the drying process is driven by the purge air flowing co-currently with the concentrate. The gaseous mixture is discharged to the atmosphere through an exhaust gas fan then directed to a stack. Dimensions of the dryer and the heating system are given in Table 1.

3.1. Effective area for heat transfer

Schlünder and Mollekopf [1] performed their investigation with batch rotating disk dryers of different diameters in which the solid was in contact with the entire heating surface. They also investigated dryers of different geometry such as rotary drum with lifters and stationary cylinder with rotating blades. Unlike rotating disc dryers, these dryers are not completely filled with solids such that only a portion of the heating surface is in contact with the solid. This fraction of the heating surface, called the effective heating surface A_EFT, is assumed equivalent to the heating surface that would have a rotating disk dryer and this is the surface area that is used in the model of the dryer presented in Figure 1.

In this work, the same concept applies to the continuous rotary-coil dryer which possesses a greater geometric complexity. Therefore, the solution is to consider the rotary-coil dryer as a rotary-disk dryer. A detailed study on the industrial copper concentrate dryer allowed determining the area and the volume of both the inner shell of the dryer and the heating mechanism of the rotary-coil dryer [21].

As mentioned above, the solid concentrate travels a distance Dz during each time interval t_R and is in contact with a fraction of the total heating area , as indicated in Eq. (21). Therefore, for the purpose of the model, the rotary-coil dryer from a national foundry can be represented by N_T rotating disk dryers connected in series, where N_T is the number of sections of the dryer of length Dz.

Unlike batch rotating-disk dryers where the solid is in contact with the entire heating surface area, the pan of the industrial copper concentrate continuous rotary-coil dryer is not completely filled such that a fraction of the heating surface is above the concentrate bed and exposed to the flow of hot gas.

According to the dryer manufacturer's specifications, the optimum utilization of the heating surface occurs when the level of concentrate above the central rotor is about a meter, resulting in a solid holdup percentage volume fraction (ϕ) of approximately 56%. The effective heat transfer surface area of the industrial rotary-coil dryer used for the copper concentrate, estimated using the geometrical dimensions of the industrial dryer, was estimated to be 237 m² [21].

3.2. Simulation Data

Data presented in Table 2 correspond to average values obtained during normal operation of the industrial dryer over a period of several months. These values were provided by engineers that were in charge of the process.

Table 3 presents the physical and thermodynamic properties of typical copper concentrate of a Chilean foundry that collaborated in this investigation and as an end-user of this model. The characterization of the concentrate samples includes the following properties: the average particle diameter, the average density of the solid particles of the dry concentrate, the effective density of the dry concentrate, and the specific heat thermal capacity of the dry concentrate.

The thermal conductivity of the dry bed was determined experimentally using a current metre (CT METRE), which consists of a controller (setting of parameters, programming and executing the desired measurement), a solid immersion measurement probe (interface between the controller and the solids sample) and a rectangular container which receives the samples for which thermal conductivity is required.

Table 2. Operational data.

Type	Parameters	Magnitude [units]
Operational	Pressure	1 [atm]
	Steam pressure in coils	11.74 [atm]
	Coil surface temperature	186 [°C]
	Rotating speed	4 [rpm]
	Concentrate hold-up	55.6 [%]
Characteristics of concentrate	Mass flow rate (dry)	41.3 [td/h]
	Initial moisture (wet)	10.5 [%]
	Exit moisture (wet basis)	0.2 [%]
	Initial solid temperature	20 [°C]
	Exit solid temperature	148 [°C]

Table 3. Physical and thermodynamic properties of the concentrate.

Properties	Magnitude [units]
Sauter mean particle diameter	21.9 [μm]
Particle density	4252 [kg/ m3]
Effective density of dry concentrate	2030 [kg/ m3]
Heat capacity of dry concentrate (100°C)	500 [J/kg K]
Effective thermal conductivity of dry bed	0.28 [W/m K]

4. Results and Discussion

Model simulations were performed using Visual Basic for Applications (VBA - Version 7 in Excel 2010). Basically, the process model iteratively calculates the value of the mixing number (N_mix) such that the value of final moisture content of the concentrate (0.2% wet basis) is achieved. When convergence has been achieved, a summary of the most relevant simulation results are recorded into an Excel spreadsheet. The process model includes model equations, initial data, and correlations to calculate the physical, thermodynamic and effective properties involved in the process. Table 4 shows the most relevant results obtained with the simulation model.

Table 4. Summary of simulation results.

Parameter/Variable	Magnitude [units]
Mixing number, Nmix	2.41
Concentrate exit temperature	148.2 [°C]
Fictitious or imaginary time of contact, tR	36 [s]
Number of sections of the dryer	76
Length of each section of the dryer, Dz	0.11 [m]

4.1. Purge air flow rate

A purge stream of hot air is fed to the dryer to remove the evaporated liquid from the surface of the particles. The purge air stream is in fact a stream of ambient air that is used to pneumatically transport the hot solid concentrate from the exit of the dryer to the solid silos and to recover a portion of the sensible heat from the hot solid concentrate. The heated ambient air is then sent to a cyclone prior to be fed to the dryer. The purge air can be considered as a resistance to mass transfer of the liquid from the interface of the particle to the gas phase. This mass transfer resistance is assumed to be negligible in this study. The purge air stream enters at a temperature of approximately 120°C and, because it is in contact with the heating surface above the bed of solid concentrate, its exit temperature reaches 135°C. Under these thermal conditions, the purge air will not reach saturation conditions and its temperature will always be above the dew point temperature, thus allowing for proper operation for the filter bag and thus minimizing concentrate particle losses to the atmosphere.

4.2. Mixing number

The mixing number (N_mix) is an empirical parameter and, according to the definition given by Schlünder and Mollekopf [1], can be viewed as the number of revolutions of the mixing device required to completely mix the bed of particles once, i.e. homogenizing the bed of particles such that the humidity and the temperature reach uniform conditions. The mixing number is considered as a purely geometrical and mechanical parameter and is identical for both wet and dry beds. A value of 2.41 was obtained in this investigation for the mixing number. This value is related on the one hand to the output moisture of the concentrate (0.2 % wet basis) and to the total length of the dryer (L_S = 8.48 m) on the other hand. There exists a unique value of the mixing number N_mix that satisfies the operating output conditions.

Hoekstra et al [22] used a bench-scale dryer to determine by regression analysis the unknown mixing parameters that allowed them to determine the drying curve at an industrial production scale with excellent results. They concluded that the mixing number could be used to scale up the dryer provided the solids do not exhibit extreme stickiness.

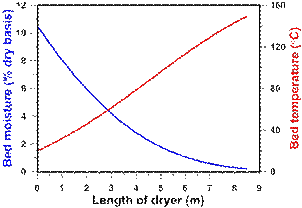
4.3. Analysis of the moisture content and temperature profiles of the copper concentrate

Figure 4 presents the profiles of the temperature and the bed moisture content along the length of the dryer predicted by the model. With respect to the relative moisture content profile, the model predicts the typical decay normally observed in concentrate moisture content along the length of the dryer. A close look at the moisture content profile, it is possible to observe that the solid concentrate has lost more than three quarters of its initial moisture content prior to reaching the midpoint location of the dryer (L = 4.24 m). This profile can be explained by considering the model of vacuum drying where there is a negligible resistance to mass transfer in addition to the assumption that the solid is saturated from the beginning of the drying process. Therefore, the heat transfer is equivalent to the absorption of the latent heat of evaporation, resulting in higher drying rates such that the moisture content decays faster.

With respect to the temperature profile of the solids along the bed, a rapid and sustained increase in temperature is observed. The decrease in the solid moisture content causes the nearly dried particles to reach temperatures beyond the saturation temperature of water. In addition, the concentrate outlet temperature simulated by the model is 148.2°C, which is very close to the actual exit concentrate temperature of 148°C.

The temperature changes more rapidly in the center portion of the bed. The rate of change at the entrance of the dryer is slightly smaller because of the colder entering solid and its sensible heat. In the last section of the dryer, the temperature increase more slowly of the decrease of temperature driving force.

The net heat flow into the bed can be calculated based on the sum of the fluxes of heat estimated using Eq. (13):

Furthermore, the net flow of the latent heat absorbed by the bed is estimated similarly to Eq. (25) using heat flux densities estimated using Eq. (14):

It is estimated via the simulation that the net heat flow (Q_in) is approximately equal to 4663 kW whereas the heat flow associated with the latent heat of evaporation (Q_lat) is 3564 kW. By performing an energy balance using the actual industrial conditions of the copper concentrate drying process, a value of Q_in of 4253 kW and an estimated value Q_lat of 3409 kW were calculated. Therefore, there is a relative good match between the simulated and the actual heat flow values.

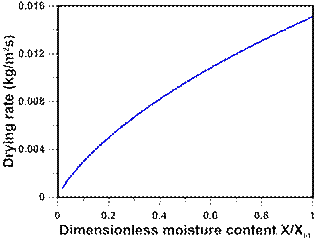
Figure 5 presents the profiles of the drying rate of the bed of concentrate as a function of the relative moisture content. The drying curve of Figure 5 is maximum at the beginning of the drying process (X/X_in = 1) because at the inlet end of the dryer the solid moisture content is at saturation temperature and, therefore, does not require heat to be used for heating the bed moisture. Then, a continuous decrease in the drying rate is observed until the ratio X/X_in finally approaches zero towards the end of the dryer. In this particular operation, a constant-rate period is not observed. The fact that the feed moisture content is relatively low also contributes to the absence of a constant-rate period.

The drying rate profile has been plotted as a function of the dimensionless moisture content (X/X_in) such that its value varies between 0 (final moisture) and 1 (initial moisture). Applying the penetration model, it is possible to obtain the drying curve as a function of the moisture content of the bed and to solve the following integral equation:

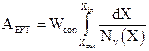
where W_con denotes the mass flow rate of the dry concentrate. The estimated residence time of the concentrate in the dryer is 2751 s, which can be obtained both using Eq. (22) and Eq. (24).

5. Conclusion

In this investigation, an industrial rotary-coil dryer used for drying copper concentrate was simulated successfully based on the model proposed by Schlünder and Mollekopf [1]. In this model, the fact that the resistance to mass transfer is negligible allows the development of a model to simulate a vacuum operation with presence of an inert purge gas. Due to the lack of experimental data internal to the solid bed, the determination of the mixing number was performed based on the inlet and outlet moisture contents of the solid bed. Simulation results for the continuous drying operation of a Chilean foundry were quite satisfactory. For obvious reasons, it was not possible to compare the simulated temperature and moisture content profiles along the length of the dryer with experimental data. Nevertheless, the predicted solid moisture content and temperature profiles are quite representative of profiles typically observed in drying operation.

In this investigation, a mixing number of 2.41 was determined. Since the mixing number is identical for wet and dry solid beds, it can be used for the industrial copper concentrate bed even though the initial moisture content varies provided that the angular frequency of the mixing device remains the same.

Acknowledgement

The authors acknowledge the financial support of DICYT-USACH - Number 051311 AG.

References