Volume 3 - Year 2016 - Pages 34-43
DOI: 10.11159/jffhmt.2016.005
Numerical Simulation of Al2O3/Automatic Transmission Fluid and Al2O3/Water Nanofluids in a Compact Heat Exchanger
Mohammed Ismail, Shahram Fotowat, Amir Fartaj
University
of Windsor, 401 Sunset Avenue, Windsor, Ontario, Canada N9B 3P4
ismailf@uwindsor.ca; fotowat@uwindsor.ca;
fartaj@uwindsor.ca
Abstract - This research presents a numerical study of the effects of nanoparticles on high viscosity fluid as well as low viscosity fluid in heat transfer characteristics. Automatic transmission fluid (ATF) and water based aluminum oxide (Al2O3) nanofluids are used in a multiport slab minichannel heat exchanger (MICHX) under laminar flow conditions. The MICHX test specimen with the test section is modelled and solved using a finite volume method based CFD code. Three different concentrations ranges from 1%-3%vol of Al2O3 nanoparticles are considered in this study. Liquids of a steady temperature of 76°C are cooled through a constant air flow rate of 507g/s and temperature of 14°C in a cross-flow orientation. Different mass flux ranging from 300 to 1200 kg/m2s are maintained for each volume concentration. The effects of volume fraction of Al2O3 nanoparticles on liquid-side heat transfer rate, dimensionless temperature, heat transfer co-efficient, and Nusselt number (Nu) are computed. The numerical results show the enhanced heat transfer coefficient for both Al2O3/ATF and Al2O3/water nanofluids. The enhancement of heat transfer coefficient of Al2O3/water is insignificant with the increase of nanoparticle volume fraction; however, it is significant for Al2O3/ATF nanofluid.
Keywords: Nanoparticles, nanofluid, automatic transmission fluid, numerical simulation, minichannel, multiport slab, aluminum oxide.
© Copyright 2016 Authors - This is an Open Access article published under the Creative Commons Attribution License terms Creative Commons Attribution License terms. Unrestricted use, distribution, and reproduction in any medium are permitted, provided the original work is properly cited.
Date Received: 2015-07-19
Date Accepted: 2016-01-13
Date Published: 2016-03-22
Nomenclature
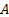 : surface area, m2
: surface area, m2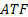 : automatic transmission
fluid
: automatic transmission
fluid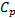 : specific heat,
: specific heat, 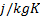
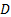 : channel diameter,
: channel diameter, 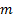
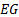 : ethylene glycol
: ethylene glycol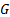 : generations of
turbulence kinetic energy,
: generations of
turbulence kinetic energy, 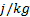 or
or 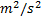
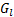 : Liquid-side mass flux,
: Liquid-side mass flux, 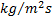
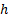 : heat transfer
coefficient,
: heat transfer
coefficient, 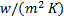
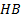 : heat balance
: heat balance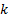 : thermal conductivity,
: thermal conductivity, 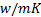
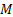 : mass flow rate,
: mass flow rate, 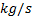
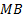 : mass balance
: mass balance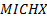 : minichannel heat
exchanger
: minichannel heat
exchanger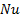 : Nusselt number
: Nusselt number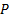 : pressure,
: pressure, 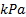
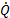 : heat transfer rate,
: heat transfer rate, 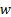
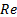 : Reynolds number
: Reynolds number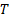 : temperature,
: temperature, 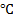
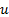 : fluid velocity,
: fluid velocity, 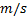
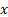 : direction x,
: direction x, 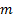
Greek Symbols
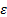 : turbulence dissipation
rate,
: turbulence dissipation
rate, 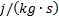 or
or 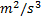
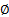 : volume fraction
: volume fraction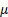 : dynamic viscosity,
: dynamic viscosity, 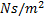 or
or 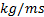
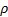 : density,
: density, 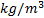
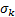 : turbulent Prandtl number
for
: turbulent Prandtl number
for 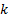
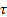 : shear stress,
: shear stress, 
Subscripts
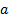 : air
: air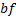 : base fluid
: base fluid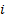 ,
, 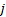 , and
, and 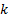 : x, y and z components
respectively
: x, y and z components
respectively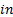 : inlet
: inlet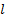 : liquid
: liquid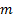 : mean
: mean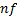 : nanofluid
: nanofluid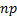 : nanoparticle
: nanoparticle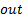 : outlet
: outlet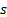 : surface
: surface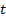 : turbulence
: turbulence
1. Introduction
Rapidly increased energy demands, space limitations, and materials savings are the key issues of everyday life, and thus a secured and available supply of energy is important for the sustainability and economic development [1]. Most of the energy using today is produced in or through the form of heat which needs to be transferred into a system or removed from the system. Enhanced heat transfer rate is a demanding challenge in rapid cooling and heating environment. In order to achieve the increased and faster heat transfer, Al2O3 nanoparticles suspensions in ATF and water are introduced due to the high thermal properties and large surface area of the nanoparticles. In addition, minichannel heat exchanger (MICHX) is employed to reduce the weight and increase the thermal performance [2]. In automotive and industrial applications, miniature heat exchanger has been becoming more popular because of its increased heat transfer flux, lighter weight, and enhanced heat transfer area density compared with conventional one [3].
The use of nanoparticles in heat transfer field was first studied at the Argonne National laboratory by Choi and Eastman [4]. In order to overcome the low heat transfer properties of common fluids, it is essential to search for the solid particles having several hundred times higher thermal conductivities than those of conventional fluids as shown by Daungthongsuk and Wongwises [5]. It is claimed that nanofluids show superior stability, rheological properties, and thermal conductivities with no penalty in pressure drop compared with suspended mili-or-micro particles.
Improvement of convective heat transfer is reported by numerous researchers [6-9]. Flow boiling heat transfer investigations are performed in laminar flow condition using low volume concentration of up to 170nm nanoparticles sizes. A heat transfer increment of up to 200% for Cu2O and Al2O3/DI-water nanofluids compared to DI-water is established. However, it is claimed that the improvement and applications of nanofluids may be slowed down by several reasons e.g. long term stability, increasing pressure drop, and nanofluids’ thermal performance in fully developed flow, lower specific heat of nanofluids, and greater cost of nanofluids preparation.
The effects
of Peclet number, volume concentration and size of ![]() -Al2O3/water and TiO2/water
nanofluids on the heat transfer behavior were investigated by Farajollahi et al
[10]. They conducted the experiment under turbulent flow condition and found
that for a particular Peclet number, heat transfer performance of TiO2/water
nanofluid at its optimum nanoparticle concentration are greater than those of
-Al2O3/water and TiO2/water
nanofluids on the heat transfer behavior were investigated by Farajollahi et al
[10]. They conducted the experiment under turbulent flow condition and found
that for a particular Peclet number, heat transfer performance of TiO2/water
nanofluid at its optimum nanoparticle concentration are greater than those of ![]() -Al2O3/water nanofluid.
Whereas,
-Al2O3/water nanofluid.
Whereas, ![]() -Al2O3/water nanofluid
possesses higher heat transfer performance at higher nanoparticle
concentration.
-Al2O3/water nanofluid
possesses higher heat transfer performance at higher nanoparticle
concentration.
The thermal performance and effects of various forces on particle distribution of the Al2O3/water nanofluid flows in a uniform wall heat flux inside a pipe, was studied by Bahiraei et al [11]. The Brownian, thermophoretic, drag, lift, and virtual mass forces were considered in their two-phase Euler-Lagrange model. They observed higher concentration of the nanoparticles in the centre of the pipe, which intensify the nonuniformity in the properties distributions and likewise flattens the velocity profile. It was also concluded that disregarding the Brownian force in the simulation causes a larger error at lower Reynolds number due to the direct dependency of the Brownian diffusion coefficient on the temperature.
Several researchers [12-14] investigated the influence of the concentration as well as the density of nanofluids to the heat transfer performance. They introduced Al2O3, CuO, TiO2, and SiO2 nanoparticles into a DI-water or an ethylene glycol (EG) and water mixture (60:40 by weight) in a variety of volume concentrations and sizes. Significantly increased Nusselt number and heat transfer coefficient of nanofluids are reported. The specific heat of Al2O3/water nanofluid is studied by Zhou et al [15] and found that the specific heat of nanofluid decreases with increase of volume fraction of nanoparticles. Moreover, Barbes et al [16] conducted an experimental study on specific heat of Al2O3/water and EG nanofluid at 25℃-65℃ temperatures and verified with the Hamilton–Crosser model.
Lee and Choi [17] conducted an investigation to evaluate the thermal conductivity of γ-Al2O3 dispersed in water. The thermal conductivity of γ-Al2O3 is three times that of water, which allows nearly three-fold increases in heat fluxes of liquid nitrogen–cooled microchannel heat exchanger. In addition, the heat transfer coefficients of several graphitic nanofluids have been studied by Yang et al [18] in a horizontal tube heat exchanger under laminar flow. They claimed that the nanoparticles improve the heat transfer coefficient of the fluid system in laminar flow. However, the improvement is found much lower than that of the predicted values obtained from the thermal conductivity correlations. The authors recommended to consider type of nanoparticles, particle loading, base fluid chemistry as well as the process temperature during preparation of nanofluids in order to improve heat transfer coefficient.
A theoretical study of the thermal conductivity of nanofuids is introduced by Xuan and Li [19]. They claimed that the nanofuids showed great potential in enhancing the heat transfer process. They stated that the volume fraction, shape, dimensions, and properties of the nanoparticles affect the thermal conductivity of nanofluids. Eastman et al [20] stated that a ‘‘nanofluid’’ consisting of copper nanoparticles dispersed in ethylene glycol (EG) has a higher effective thermal conductivity than either pure EG or CuO/EG.
CuO nanoparticles in EG/water (60:40) of 0% to 6.12% at temperature of −35℃ to 50℃ are studied by Namburu et al [21]. They stated that the viscosity of nanofluid decreases exponentially as the temperature increases. The relative viscosity of CuO nanofluid increases with the increase of %vol and decreases substantially with temperature for higher concentration. Furthermore, Garg et al [22] investigated the thermal conductivity and viscosity of 2%vol CuO nanoparticles in water/EG and claimed that the thermal conductivity is twice that of the Maxwell model and the viscosity is about four times that of the predicted value of Einstein model [23].
The viscosity and thermal conductivity of 21nm TiO2 nanoparticles in DI-water up to a volume fraction of 3% of particles at temperatures of up to 55℃ were also examined by Turgut et al [24]. They established that the thermal conductivity of the nanofluid increases with an increase of particle volume fraction, and the enhancement is observed to be 7.4% higher than the base fluid at 13℃. Moreover, Elçioğlu [25] experimentally and analytically studied the viscosity of Al2O3/water nanofluid for different nanoparticle volumetric fractions, nanoparticle diameters, and temperatures. Their results showed that the viscosity of Al2O3/water nanofluid increases with the nanoparticle diameter and decreases exponentially with temperature. Experimental investigations are performed to determine the viscosity of TiO2 and Al2O3 nanoparticles suspended in a mixture of EG/water. Another experimental study at various volume fractions between 0% and 4% and a temperature range of 15℃–60℃ is conducted by Yiamsawas et al [26]. Results indicate that the theoretical models are not suitable to predict the viscosity of nanofluids.
Study on heat transfer characterization of ATF based Al2O3 nanofluid in narrow channels is very rare in open literatures. Therefore, the current study dealing with ATF and water based Al2O3 nanofluid heat transfer characteristics might supplement the useful information for industrial applications. The main purpose of this study is to evaluate the dimensionless temperature and heat transfer characteristics of ATF and water/Al2O3 nanofluids as a homogeneous single-phase fluid in a MICHX.
2. Numerical Method
The numerical simulation is performed in a serpentine slab multiport minichannel heat exchanger (MICHX) as shown in Fig. 1a and Fig. 1b.

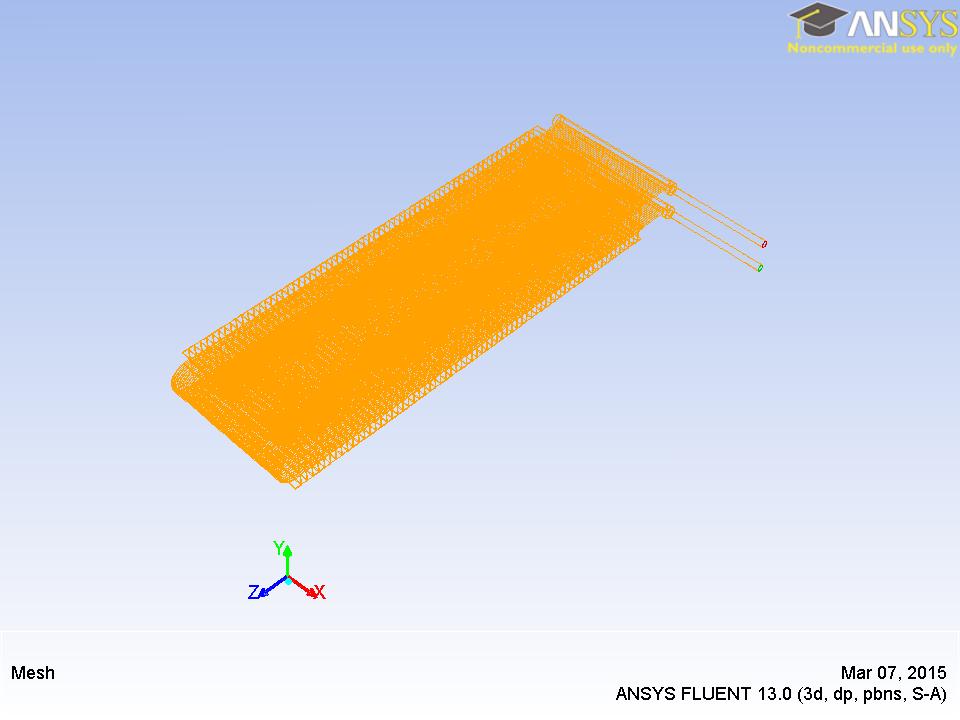

The specifications of the MICHX are presented below in Table. 1.
Table 1. Specifications of MICHX [27].
| Parameters | Magnitudes | |
| Materials of MICHX | Aluminum | |
| Number of channels | 68 | |
| Channel diameter | 1mm | |
| Port to port distance | 1.463mm | |
| Slab | length (x-axis) | 304mm |
| thickness (y-axis) | 2mm | |
| width (z-axis) | 100mm | |
| Inner dia. of serpentine curve | 20mm | |
| Inner dia. of Header | 4.76mm | |
| Fin | density | 8 fins/25.4mm |
| height: middle | 20 mm | |
| height: top & bottom | 10 mm | |
| thickness | 0.1 mm | |
Since the suspended particles in nanofluid are very fine, the particles may easily be fluidized; subsequently, by overlooking the slip motion between particles and fluid and assuming the base fluid and the nanoparticles are in thermal equilibrium, the nanofluid has been treated as a homogenous fluid. The following time-averaged instantaneous governing equations are used to compute steady state and incompressible fluid flow without chemical reaction:
Continuity:
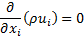
Momentum:
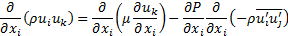
Energy:
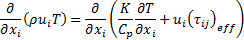
Turbulence kinetic energy:
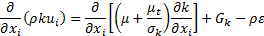
The main challenge of this approach is to calculate the thermos-physical properties of nanofluid. For a single-phase model, the following equations are used to compute the thermophysical properties of nanofluids:
Density:
Applying the
principle of mass conservation of the two species in a finite control volume of
the nanofluid, the density of nanofluid, ![]() is
obtained from the (Pak and Cho correlation [28] correlation as:
is
obtained from the (Pak and Cho correlation [28] correlation as:
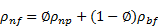
Where ![]() is the volumetric fraction of nanoparticles in
the base fluid,
is the volumetric fraction of nanoparticles in
the base fluid, ![]() is the density of nanoparticles, and
is the density of nanoparticles, and ![]() is the density of base fluid. This equation is
frequently used by several researchers [12], [25], [29-32] for calculating the
density of nanofluids.
is the density of base fluid. This equation is
frequently used by several researchers [12], [25], [29-32] for calculating the
density of nanofluids.
Specific heat:
The thermal conservation of energy of the two species in a finite control volume yields the overall specific heat of the nanofluid [32]. For calculating the specific heat of nanofluid, (Xuan and Roetzel [33] correlation is used. The equation is
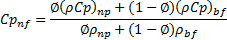
Where ![]() and
and ![]() represent the specific heat of nanoparticles and
base fluid respectively. It is an advanced form of Pak and Cho [28] correlation
and used by many researchers [12], [16], [29-30], [32].
represent the specific heat of nanoparticles and
base fluid respectively. It is an advanced form of Pak and Cho [28] correlation
and used by many researchers [12], [16], [29-30], [32].
Thermal conductivity:
There are numerous correlations to evaluate the thermal conductivity of nanofluid. Yu and Choi [34] correlation, which is the simplified form of Hamilton and Crosser [35] correlation of single phase homogeneous nanofluid of spherical nanoparticles is used in this study. The correlation is
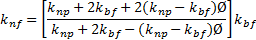
where ![]() and
and ![]() represent the thermal conductivity of
nanoparticles and base fluid respectively.
represent the thermal conductivity of
nanoparticles and base fluid respectively.
Dynamic viscosity:
For calculating the dynamic viscosity of nanofluids, Brinkman [36] correlation is used in this study. The correlation is
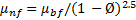
This is an advanced form of the well-known Einstein’s model [23], and applicable to moderate particle volume concentration less than 4%.
2. 1. Boundary conditions
For both
liquid-side and air-side, temperature and mass flow rate boundary conditions
are applied at the inlet, and pressure outlet condition is specified at the out
let. The inlet temperature of the liquid is kept constant at 76![]() while the mass fluxes are varied from 300 to 1200
kg/m2s. For the air-side, a constant mass flow rate of 507g/s and a
constant temperature of 14
while the mass fluxes are varied from 300 to 1200
kg/m2s. For the air-side, a constant mass flow rate of 507g/s and a
constant temperature of 14![]() are applied at the inlet of the test chamber.
are applied at the inlet of the test chamber.
An adiabatic or zero heat flux boundary condition is employed at the walls of the manifolds, serpentine bend, and test chamber. A no-slip boundary condition is applied on the wall for fluids.
2. 2. Grid independency and model validation
In order to validate the model, a numerical verification including a grid dependence study and an overall error in mass balance (MB) and heat balance (HB) is performed. The detail of the grid independency study is previously published [27] and is not repeated here. The errors in MB and HB are defined as
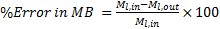
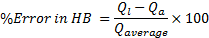
The overall error in mass balance between liquid inlet and outlet mass flow rates and heat balance between air-side and liquid-side heat transfer rates in all cases of simulations considered in this study is observed in a range of ±0.11% and 0.85% respectively.
In addition, a set of simulation results of water and 50:50 ethylene glycol-water mixture (EG) were compared with experimental results of Khan and Fartaj [1] as shown in Fig. 2. The figure shows a very good agreement with the experimental measured data and ensures accuracy and reliability of the model and its simulation results.
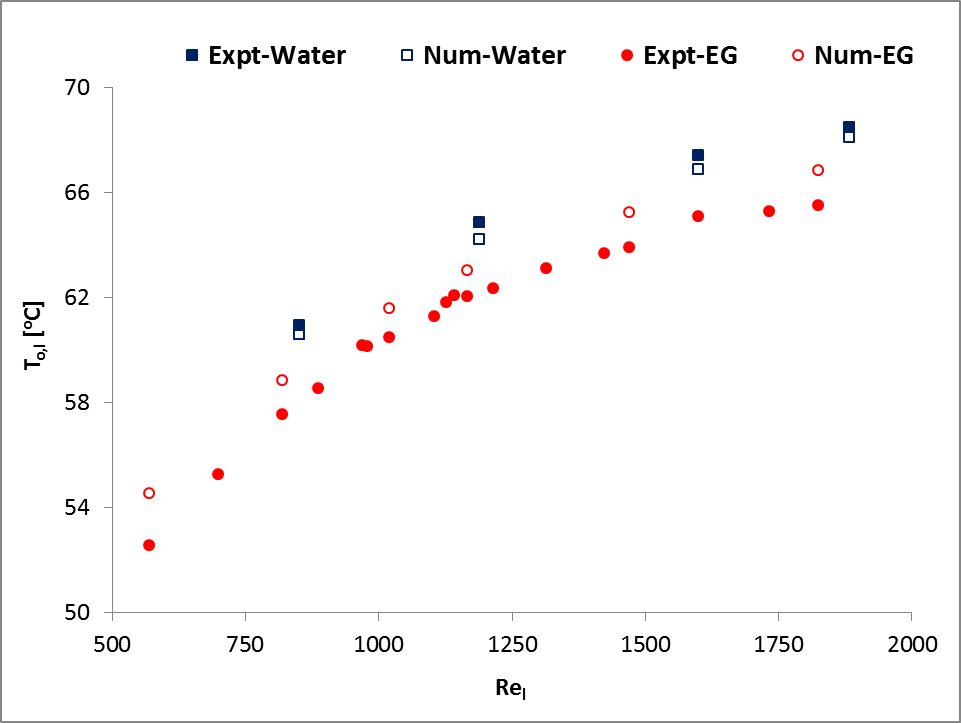

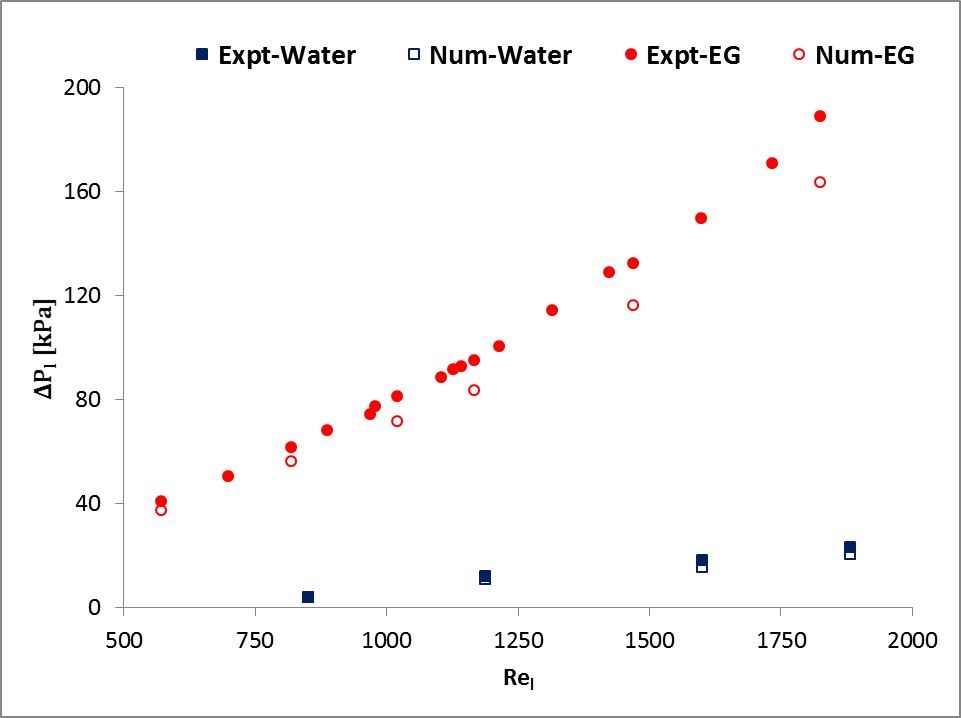
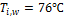 and
and 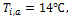 for water cooling;
for water cooling; 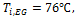 and
and 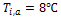 for EG cooling].
for EG cooling].3. Results and Discussions
3.
1. Centreline velocity (![]() )
)
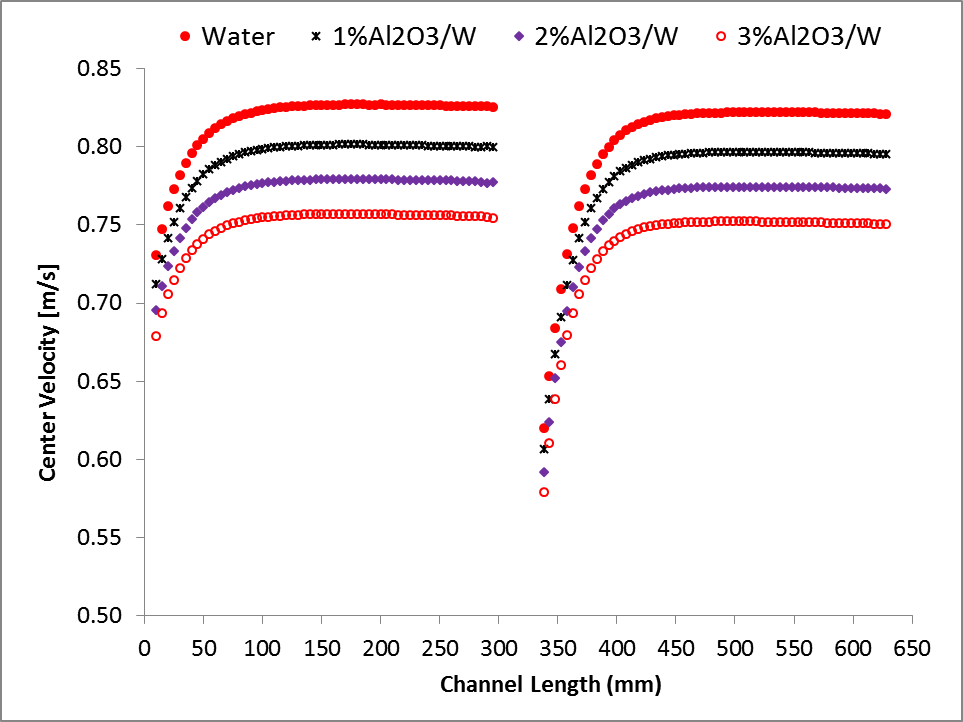
The variations of centreline velocity of liquid streams at the top and bottom slabs along the length of the channel are shown in Fig. 3. It shows that a hydrodynamic boundary layer develops along the channels when liquid flows in the channels at the top and bottom slabs. The flow becomes hydro-dynamically fully developed before entering to the serpentine and leaving from MICHX. For the same mass flux of the liquid, the centreline velocity is lower for higher volume fraction.
3. 2. Heat transfer
coefficient (![]() )
)

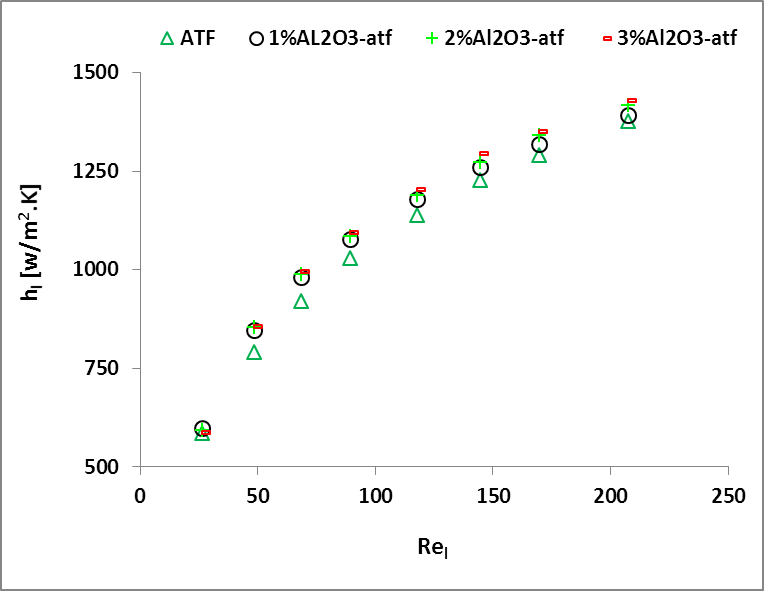
The
variations of the liquid-side heat transfer coefficient (![]() ) with different concentration (
) with different concentration (![]() ) and Reynolds number (
) and Reynolds number (![]() ) are shown in Figs. 4a and 4b . The figures
illustrate that
) are shown in Figs. 4a and 4b . The figures
illustrate that ![]() increases nonlinearly with the increase of
increases nonlinearly with the increase of ![]() . It is found that the enhancement of
. It is found that the enhancement of ![]() for Al2O3/water nanofluid
is 4.4%-5.3%. However, the trend indicates insignificant enhancement of
for Al2O3/water nanofluid
is 4.4%-5.3%. However, the trend indicates insignificant enhancement of ![]() with the increase of
with the increase of ![]() . It is also observed that the enhancement of
. It is also observed that the enhancement of ![]() for Al2O3/ATF nanofluid is
2.4%-6.4%, which shows a lower improvement in heat transfer coefficient for lower
volume concentration; but the enhancement increases significantly with the
increase of concentration.
for Al2O3/ATF nanofluid is
2.4%-6.4%, which shows a lower improvement in heat transfer coefficient for lower
volume concentration; but the enhancement increases significantly with the
increase of concentration.
3. 3. Dimensionless
Temperature (![]() )
)
The
dimensionless temperature (![]() ) is defined as the ratio of the liquid side
temperature drop to the maximum temperature difference between air and liquid.
The dimensionless temperature,
) is defined as the ratio of the liquid side
temperature drop to the maximum temperature difference between air and liquid.
The dimensionless temperature, ![]() is defined as
is defined as
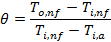
where, ![]() outlet temperature of the nanofluid,
outlet temperature of the nanofluid, ![]() ,
, ![]() inlet temperature of the nanofluid,
inlet temperature of the nanofluid, ![]() , and
, and ![]() inlet
temperature of air,
inlet
temperature of air, ![]() .
.
Fig. 5 shows the variations of mass flux and nanofluids concentration on the dimensionless temperature.
At a
particular mass flux, it is observed from the graph that the liquid side
temperature drop is higher for ATF than water. Also, the ![]() decreases nonlinearly with the increase of
liquid-side mass flux (Gl). Moreover, owing to its larger heat conduction,
higher nanofluids concentration shows higher dimensionless temperature which
indicates higher temperature drop for a constant mass flux.
decreases nonlinearly with the increase of
liquid-side mass flux (Gl). Moreover, owing to its larger heat conduction,
higher nanofluids concentration shows higher dimensionless temperature which
indicates higher temperature drop for a constant mass flux.

3. 4. Convective heat
transfer coefficient (![]() )
)
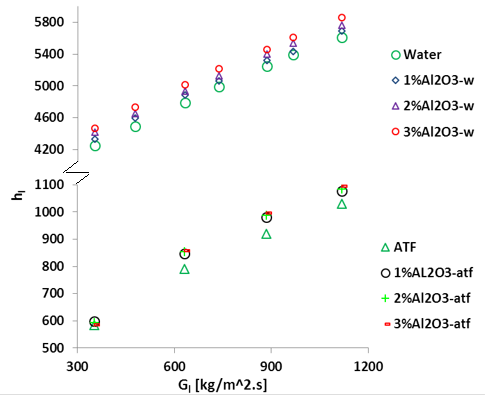
The heat transfer coefficient is an important parameter for heat exchanger design. The heat transfer coefficient of liquid, hl is defined as
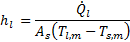
Where ![]() is the liquid-side heat transfer rate,
is the liquid-side heat transfer rate, ![]() is the total heat transfer surface area,
is the total heat transfer surface area, ![]() is the liquid mean temperature, and
is the liquid mean temperature, and ![]() is the mean surface temperature.
is the mean surface temperature.
The
liquid-side heat transfer rate, ![]() is defined as
is defined as
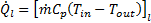
Where ![]() ,
, ![]() ,
, ![]() , and
, and ![]() represent the mass flow rate, specific heat,
inlet temperature, and outlet temperature respectively.
represent the mass flow rate, specific heat,
inlet temperature, and outlet temperature respectively.
The liquid
side heat transfer coefficient (ℎl) vs mass flux (![]() ) for ATF and water at
various nanofluid concentrations is illustrated in Fig. 6. It shows that ℎl increases with
the increase of
) for ATF and water at
various nanofluid concentrations is illustrated in Fig. 6. It shows that ℎl increases with
the increase of ![]() and is higher for water than ATF as expected.
Results also show that effect of Al2O3 nanoparticles on
the heat transfer coefficient higher for low viscosity fluid (Al2O3/water)
than that of high viscosity fluid (Al2O3/ATF). For a
particular
and is higher for water than ATF as expected.
Results also show that effect of Al2O3 nanoparticles on
the heat transfer coefficient higher for low viscosity fluid (Al2O3/water)
than that of high viscosity fluid (Al2O3/ATF). For a
particular ![]() , the increase of ℎl becomes
2.4%-6.4% for ATF and 4.4%-5.3% for water in the range of 1%vol≤∅≤3%vol.
, the increase of ℎl becomes
2.4%-6.4% for ATF and 4.4%-5.3% for water in the range of 1%vol≤∅≤3%vol.
However, at a particular mass flux of 300kg/m2s, there is no significant improvement on heat transfer coefficient for Al2O3/ATF nanofluid. This is due to the counteract effect of the specific heat against the heat transfer coefficient improvement.
3. 5. Nusselt Number (Nu)
The Nusselt number of liquid (Nul) is calculated by using the following equation;
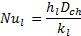
Where d and ![]() represent the hydraulic diameter of the channel
and the thermal conductivity of liquid respectively.
represent the hydraulic diameter of the channel
and the thermal conductivity of liquid respectively.
Fig. 7 shows
the effects of ![]() on
on ![]() for nanofluid concentration from 1% to 3% at
constant inlet liquid temperature of 76
for nanofluid concentration from 1% to 3% at
constant inlet liquid temperature of 76 ![]() and air temperature of 14
and air temperature of 14 ![]() . It shows that the 𝑁𝑢l increases
nonlinearly with the increase of Gl. The slop of 𝑁𝑢l is found
steeper at lower
. It shows that the 𝑁𝑢l increases
nonlinearly with the increase of Gl. The slop of 𝑁𝑢l is found
steeper at lower ![]() compared with those of higher
compared with those of higher ![]() . 𝑁𝑢l is found to be
higher for lower concentration because its thermal conductivity dominates the 𝑁𝑢l compared with
heat transfer coefficient of nanofluids.
. 𝑁𝑢l is found to be
higher for lower concentration because its thermal conductivity dominates the 𝑁𝑢l compared with
heat transfer coefficient of nanofluids.
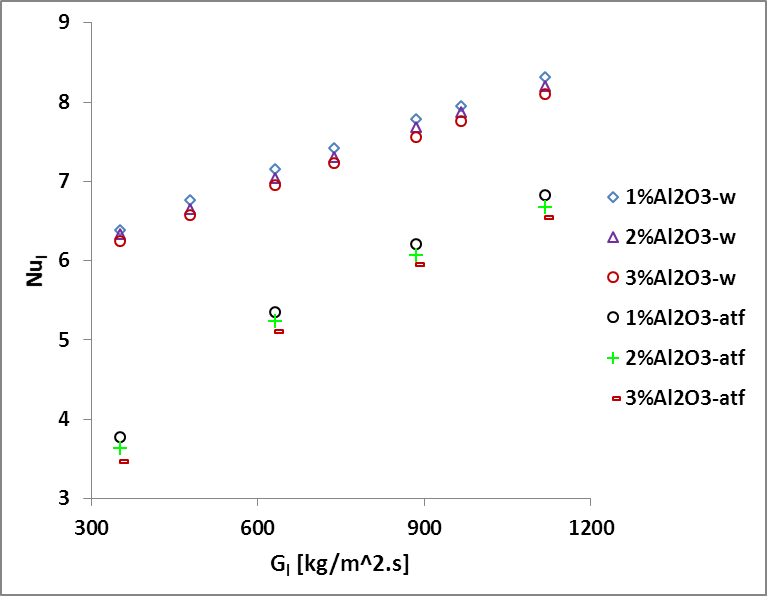
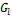 and nanofluid concentration on
and nanofluid concentration on 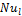 .
.4. Conclusions
In this study, the effects of nanoparticles in low and high viscosity fluids on heat transfer characteristics are conducted in a multiport slab compact heat exchanger. The volume concentrations of Al2O3/ATF and Al2O3/water nanofluids are varied from 1%≤∅≤3%. The constant inlet temperatures of liquid and air are maintained at 76℃ and 14℃ respectively in all simulations.
It is found
that the flow reaches hydro-dynamically fully developed before entering to the
serpentine and leaving from MICHX. For the same mass flux of the liquid, the
centreline velocity is lower for higher volume fraction. As it is expected, the
heat transfer coefficient, ℎl increases with
the increase of mass velocity, ![]() . For a particular
. For a particular ![]() , heat transfer coefficient of fluids are higher
for higher concentration of nanoparticles. The enhancement of
, heat transfer coefficient of fluids are higher
for higher concentration of nanoparticles. The enhancement of ![]() for Al2O3/water nanofluid
is 4.4%-5.3%. But, the trend indicates insignificant enhancement of
for Al2O3/water nanofluid
is 4.4%-5.3%. But, the trend indicates insignificant enhancement of ![]() with the increase of
with the increase of ![]() .
.
The improvement of ℎl for Al2O3/ATF nanofluid is 2.4%-6.4%, which displays a lower improvement in heat transfer coefficient for lower volume fraction; however, the significant enhancement of ℎl is observed for higher volume fraction. 𝑁𝑢𝑛𝑓 is observed lower than 𝑁𝑢bf due to its dominating thermal conductivity.
References
[1] M. G. Khan and A. Fartaj, "A review on microchannel heat exchangers and potential applications," International Journal of Energy Research, vol. 35, no. 7, pp. 553-582, 2011. View Article
[2] M. Ismail, S. Fotowar and A. Fartaj, "Effect of channel size on heat transfer and pressure drop in thin slabs minichannel heat exchanger," International Journal of Mechanical Engineering and Mechatronics, vol. 2, no. 1, pp. 33-42, 2014. View Article
[3] M. Ismail, S. Fotowar and A. Fartaj, "Study of Al2O3/water nanofluid in a multiport slab heat exchanger," in Proc. of the 25th Canadian Congress of Applied Mechanics (CANCAM), London, Canada, 2015. View Article
[4] S. Choi and J. A. Eastman, Enhancing thermal conductivity of fluids with nanoparticles, Argonne, IL: Argonne National Laboratory, 1995. View Book
[5] W. Daungthongsuk and S. Wongwises, "A critical review of convective heat transfer of nanofluids," Renewable and Sustainable Energy Reviews, vol. 11, no. 5, pp. 797-817, 2007. View Article
[6] A. Dominic, J. Sarangan, S. Suresh and M. Sai, "Heat transfer performance of Al2O3/water nanofluids in a mini channel heat sink," Journal of Nanoscience and Nanotechnology, vol. 14, no. 3, pp. 2368-2376, 2014. View Article
[7] S. Z. Heris, Z. Edalati, S. H. Noie and O. Mahian, "Experimental iInvestigation of Al2O3/Water nanofluid through equilateral triangular duct with constant wall heat flux in laminar flow," Heat Transfer Engineering, vol. 35, no. 13, pp. 1173-1182, 2014. View Article
[8] E. Nourafkan, G. Karimi and J. Moradgholi, "Experimental study of laminar convective heat transfer and pressure drop of cuprous oxide/water nanofluid inside a circular tube," Experimental Heat Transfer, vol. 28, no. 1, pp. 58-68, 2015. View Article
[9] J.-Y. Jung, H.-S. Oh and H.-Y. Kwak, "Forced convective heat transfer of nanofluids in microchannels," International Journal of Heat and Mass Transfer, vol. 52, no. 1-2, pp. 466-472, 2009. View Article
[10] B. Farajollahi, S. G. Etemad and M. Hojjat, "Heat transfer of nanofluids in a shell and tube heat exchanger," International Journal of Heat and Mass Transfer, vol. 53, pp. 12-17, 2010. View Article
[11] M. Bahiraei and S. M. Hosseinalipour, "Effects of various forces on particle istribution and thermal features of suspensions containing alumina nanoparticles," Journal of Dispersion Science and Technology, vol. 35, pp. 859-867, 2014. View Article
[12] J. Albadr, S. Tayal and M. Alasadi, "Heat transfer through heat exchanger using Al2O3 nanofluid at different concentrations," Case Studies in Thermal Engineering, vol. 1, no. 1, pp. 38-44, 2013. View Article
[13] A. M. Hussein, K. V. Sharma, R. A. Bakar and K. Kadirgama, "The effect of nanofluid volume concentration on heat transfer and friction factor inside a horizontal tube," Journal of Nanomaterials, pp. 1-12, 2013. View Article
[14] R. S. Vajjha and D. K. Das, "Specific heat measurement of three nanofluids and development of new correlations," Journal of Heat Transfer, vol. 131, no. 7, pp. 071601-1-7, 2009. View Article
[15] S.-Q. Zhou and R. Ni, "Measurement of the specific heat capacity of water-based Al2O3 nanofluid," Applied Physics Letters, vol. 92, no. 9, pp. 093123-1-3, 2008. View Article
[16] B. Barbes, R. Paramo, E. Blanco, M. J. Pastoriza-Gallego, M. M. Pineiro, L. L. Legido and C. Casanova, "Thermal conductivity and specific heat capacity measurements of Al2O3 nanofluids," J. Therm. Anal. Calorim, vol. 111, no. 2, pp. 1615-1625, 2013. View Article
[17] S. Lee and S. Choi, "Application of metallic nanoparticles suspensions in advanced cooling systems," in Proc. of 1996 Int. Mechanical Engineering Congress and Exhibition, Atlanta, USA, 1996. View Article
[18] Y. Yang, G. Z. Zhang, E. A. Grulke, W. B. Anderson and G. Wu, "Heat transfer properties of nanoparticle-in-fluid dispersions (nanofluids) in laminar flow," International Journal of Heat and Mass Transfer, vol. 48, no. 6, pp. 1107-1116, 2005. View Article
[19] Y. Xuan and Q. Li, "Heat transfer enhancement of nanofluids," Int. J. Heat and Fluid Flow, vol. 21, no. 1, pp. 58-64, 2000. View Article
[20] J. A. Eastman, S. U. S. Choi, S. Li, W. Yu and L. J. Thompson, "Anomalously increased effective thermal conductivities of ethylene glycol-based nanofluids containing copper nanoparticles," Applied Physics Letters, vol. 78, no. 6, pp. 718-720, 2001. View Article
[21] P. K. Namburu, D. P. Kulkarni, D. Misrab and D. K. Das, "Viscosity of copper oxide nanoparticles dispersed in ethylene glycol and water mixture," Experimental Thermal and Fluid Science, vol. 32, no. 2, pp. 397-402, 2007. View Article
[22] J. Garg, B. Poudel, M. Chiesa, J. B. Gordon, J. J. Ma, J. B. Wang, Z. F. Ren, Y. T. Kang, H. Ohtani, J. Nanda, G. H. McKinley and G. Chen, "Enhanced thermal conductivity and viscosity of copper nanoparticles in ethylene glycol nanofluid," Journal of Applied Physics, vol. 103, pp. 074301-1-6, 2008. View Article
[23] A. Einstein, "A new determination of molecular dimensions," Annln. Phys., vol. 19, no. 4, pp. 289-306, 1906.
[24] A. Turgut, L. Tavman, M. Chirtoc, H. P. Schuchmann, C. Sauter and S. Tavman, "Thermal conductivity and viscosity measurements of water-based TiO2 nanofluids," Int. J. Thermophys, vol. 30, no. 4, p. 1213-1226, 2009. View Article
[25] E. B. Elçioğlu, "Experimental and theoretical investigations on alumina-water nanofluid viscosity with statistical analysis," Thesis, Middle East Technical University, Turkey, 2013. View Article
[26] T. Yiamsawas, O. Mahian, A. S. Dalkilic, S. Kaewnai and S. Wongwises, "Experimental studies on the viscosity of TiO2 and Al2O3 nanoparticles suspended in a mixture of ethylene glycol and water for high temperature applications," Applied Energy, vol. 111, pp. 40-45, 2013. View Article
[27] M. Ismail, A. Fartaj and M. Karimi, "Numerical investigation on heat transfer and fluid flow behaviors of viscous fluids in a minichannel heat exchanger," Numerical Heat Transfer, Part A, vol. 64, no. 1, pp. 1-29, 2013. View Article
[28] B. C. Pak and Y. I. Cho, "Hydrodynamic and heat transfer study of dispersed fluids with submicron metallic oxide particles," Experimental Heat Transfer, vol. 11, no. 2, pp. 151-170, 1998. View Article
[29] S. Goktepe, K. Atalık and H. Ertürk, "Comparison of single and two-phase models for nanofluid convection at the entrance of a uniformly heated tube," International Journal of Thermal Sciences, vol. 80, pp. 83-92, 2014. View Article
[30] M. Akhtari, M. Haghshenasfard and M. R. Talaie, "Numerical and experimental investigation of heat transfer of α-Al2O3/water nanofluid in double pipe and shell and tube heat exchangers," Numerical Heat Transfer, Part A, vol. 63, no. 12, p. 941-958, 2013. View Article
[31] P. C. M. Kumar, J. Kumar and S. Suresh, "Experimental investigation on convective heat transfer and friction factor in a helically coiled tube with Al2O3/water nanofluid," Journal of Mechanical Science and Technology, vol. 27, no. 1, pp. 239-245, 2013. View Article
[32] W. H. Azmi, K. V. Sharma, R. Mamat, A. B. S. Alias and I. I. Misnon, "Correlations for thermal conductivity and viscosity of water based nanofluids," in 1st International Conference on Mechanical Engineering Research (ICMER 2011), 2012. View Article
[33] Y. Xuan and W. Roetzel, "Conceptions for heat transfer correlation of nanofluids," International Journal of Heat and Mass Transfer, vol. 43, no. 19, pp. 3701-3707, 2000. View Article
[34] W. Yu and S. Choi, "The role of interfacial layers in the enhanced thermal conductivity of nanofluids: A Renovated Maxwell Model," Journal of Nanoparticle Research, vol. 5, no. 1-2, pp. 167-171, 2003. View Article
[35] R. L. Hamilton and O. K. Crosser, "Thermal two-com conductivity of heterogeneous two-component systems," I & EC Fundamentals, vol. 1, no. 3, pp. 187-191, 1962. View Article
[36] H. C. Brinkman, "The viscosity of concentrated suspensions and solutions," The Journal of Chemical Physics, vol. 20, no. 4, p. 571, 1952. View Article

