Journal of Fluid Flow, Heat and Mass Transfer (JFFHMT)

ISSN: 2368-6111

1. Introduction

The cardiovascular system transports oxygen and nutrients to all the tissues of the body, from where it removes carbon dioxide and other harmful waste products of cell metabolism. From a physical point of view, the system consists of a pump that propels a viscous liquid (the blood) through a network of flexible tubes. The heart provides energy to move blood through the circulatory system and is one key component in the complex control mechanism of maintaining pressure in the vascular system ([20]). The aorta is the main artery originating from the left ventricle and then bifurcates to other arteries, and is identified by several segments (ascending, thoracic, abdominal). There are several features of the aorta that have an effect on the blood flow, such as the tapering of the aorta or the fact that ascending aorta is arched (curved). Still, the functionality of the aorta, considered as a single segment, is worth exploring from a modeling perspective, in particular in relationship to the presence of the aortic valve.

There has been extensive literature describing the dynamics of the vascular network coupled with a heart model (e.g. [1], [7], [8], [9], [10], [16], [17]), the majority focusing on either a detailed description of the four chambers of the heart or on the spatial dynamics in the aorta, but not on both. In fact, there seem to be no studies addressing the heart rate variability based on the detailed spatial description of the pressure and flow patterns in the aorta. More broadly, theory and applications of optimization and control in spatial networks have been extensively developed in literature, and several numerical approaches have been successfully applied to telecommunications, transportation or supply networks ([5], [6], [15]).

In this paper we propose to capture through simulation and optimization the dynamics of the pressure and flow in the aorta as well as the heart rate variability. We take into account the elasticity of the aorta, considered as a single vessel, together with an aortic valve model at the inflow and a peripheral resistance model at the outflow (Section 2). We develop a numerical scheme to find approximate solutions to the system (Section 3) and then we describe and simulate a control mechanism for maintaining constant mean pressure in the aorta by allowing for variable heart rate and peripheral resistance (Section 4). Finally, we propose a spectral discretization of the optimal control problem to simulate this phenomenon (Section 5). The novelty of this paper is in considering the boundary control problem for a 1D PDE coupled with a valve model, which translates to a Dirichlet boundary condition for pressure during systole and for flow during diastole. The switch between the two type of boundary conditions is not prescribed a priori in time, but rather it is a function of the computed solution in time. This make the synthesis of the optimal control to be a non-standard problem, which is difficult to solve theoretically so we propose instead an effective numerical approach.

2. Mathematical Model

We start with the standard hyperbolic system (see [2], [14], [21]) which models cross-section area A(x,t) and average velocity u(x,t) in the spatial domain:

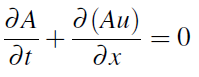
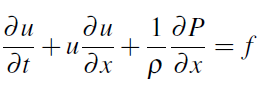
where f = f (x,t) is a friction force, usually taken to be , μ is the fluid viscosity, and P(x,t) is the hydrodynamic pressure. Here we include the inertial effects of the wall motion, described by the wall displacement :

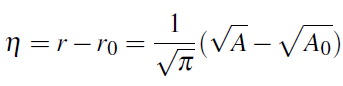
The fluid structure interaction is modeled using inertial forces, which gives the pressure law (see [3], [7])

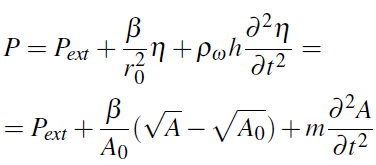
where r(x,t ) is the radius, r₀(x,t); A₀ = A(x0); P_ext is the external pressure, , σ is the Poisson ratio (usually taken to be , E is Young modulus, h is the wall thickness, , ρ_ω is the density of the wall. The relation (4) was obtained by putting:

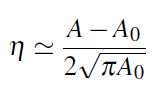This leads to the following Boussinesq system:

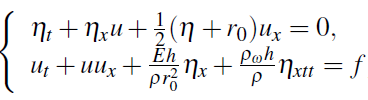
where ρ is the blood density. Considering the relation , we get the system:

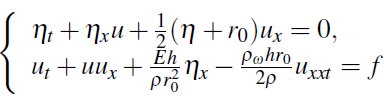
or, rearranging terms in u,

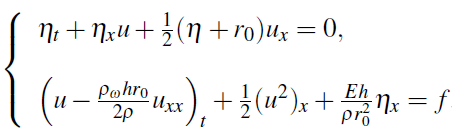
If we use cross-section area instead of the wall displacement, we have

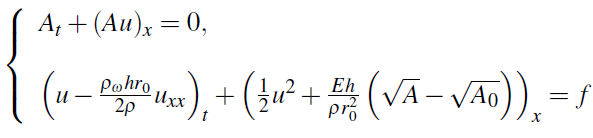
which can be written in compact form:

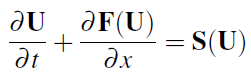
where

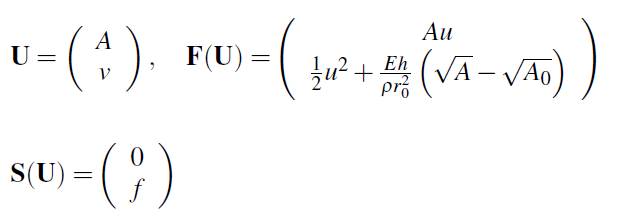
and is the solution of the boundary value problem

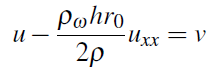
together with boundary conditions that are indicated below.

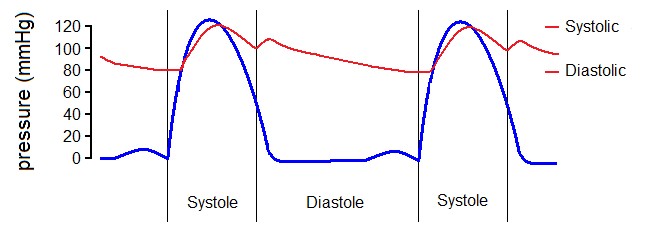
Inflow conditions (at x = 0) are implemented using a valve model, which mimics the real behavior of the physiological system. The aortic valve is one of the two semilunar valves of the heart and lies between the left ventricle and the aorta. It permits the flow of the blood from the left ventricle of the heart to the aorta. During ventricular systole, pressure rises in the left ventricle. When the pressure in the left ventricle rises above the pressure in the aorta, the aortic valve opens, allowing blood to exit the left ventricle into the aorta. When ventricular systole ends, pressure in the left ventricle rapidly drops. When the pressure in the left ventricle decreases below the aortic pressure, the aortic valve closes, and remains closed until the next heart beat. The opening and closing of valve is determined by the pressure difference between the left ventricle (P_LV(t) ) and the aortic pressure. More specifically, the valve opens when

in which case the pressure at the inflow gets prescribed

and it closes when the velocity becomes negative, in which case the velocity at the inflow is prescribed to be zero:

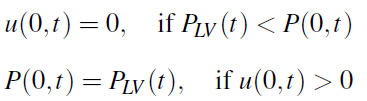
in which case the pressure at the inflow gets prescribed

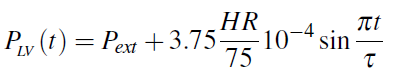
with HR representing the heart rate and t the duration of the systole, taken to be a quarter of the heart beat (τ = 15/HR). This model accounts for the fact that peak amplitude of the left ventricular pressure depends on the heart rate.

As terminal condition, we have used a model with terminal reflection coefficient R_t, (see [2]), which is based on the assumption that W_b is proportional to W_f:

where Here W_b is the backward characteristic and W_f is the forward characteristic of the hyperbolic system (9):

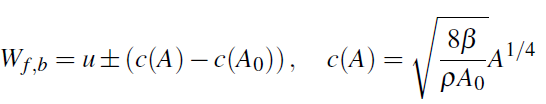
Note that R_t = 1 corresponds to u = 0, which means the outflow is completely blocked, while R_t = -1 corresponds to A = A₀. For general values of the boundary conditions is

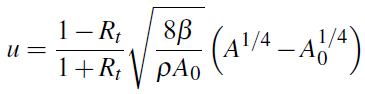
This is a nonlinear relation between the two components (area and velocity) of the system of PDEs.

We note that the reduced 1D model (1)–(2) can be derived ([21]) from the full 3D fluid flow equations under both the assumption of newtonian or non-newtonian nature for the fluid, the difference being in the nonlinearity of the velocity. Here we followed the standard non-newtonian assumption of a blunt velocity profile across the vessel wall, which is typical for blood flow in large arteries. Alternative (and more realistic) models for the rheology of the blood (such as Casson model, [18], [23], which assumes a nonlinear stress strain relation for the fluid) will lead to different expressions for the friction forces in the reduced model and to different nonlinear terms for the momentum equation. While these models are worth considering for a more realistic mathematical model (see also comments in the conclusion section), for the scope of the present paper it is sufficient to stay with simplest model for the fluid and fluid structure interactions, since we do not expect significantly different qualitative conclusions if we were to incorporate other models.

3. Numerical Discretization

In order to solve the system (9)–(11) on Ω = [0;L] we use a discontinuous Galerkin scheme for the first equation and a spectral method for the second one.

We write the weak formulation of the problem, approximate U(x,t) with its discretized expansion and integrate twice by part (for details see [21]), so we get:

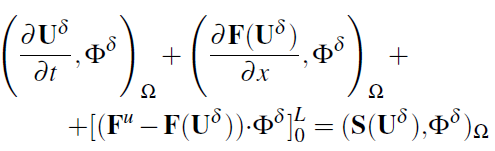
To simplify the method, we have mapped each elemental region onto the standard element . This mapping is defined as

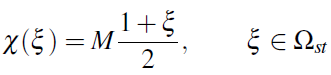
and its inverse is given by

.

We selected as expansion basis the Legendre polynomials , with k the polynomial order, because they are orthogonal with respect to the product inner product of L². In this way, the solution is expanded on Ω as

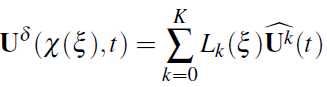
with the time-varying coefficients of the expansion. We have chosen Legendre points (which are the zeros of Legendre polynomials) as collocation points. Replacing (13) in (12) and letting , we obtain the following system of 2(K + 1) differential equations to be solved:

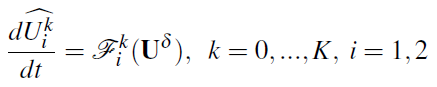
where , are each of the two components of and

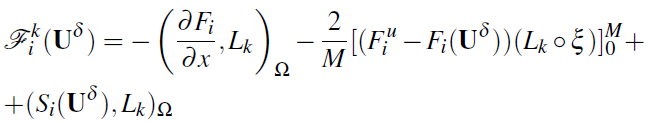
with M as the length of the edge. The method is completed with a second-order Adams-Bashforth timeintegration scheme:

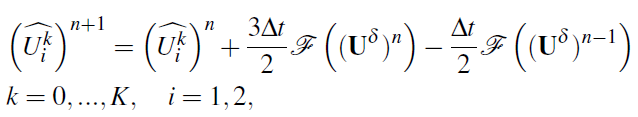
in which is the time step and n the number of every time step. To calculate the integrals we use a Gauss quadrature formula of order

The upwinded fluxes are computed solving a Riemann problem that takes into account the characteristic information moving away. At a time t, each interface separates two constant states, and , and we need to determine the two upwinded states, and (, originated on each side of interface at time . To do this, the following equations are required:

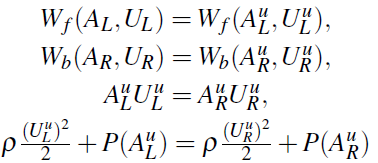
The first two equations come from the assumption that the flow between two initial states is inviscid, and the forward characteristic information, W_f , and the backward characteristic information,W_b:

To approximate the second order derivative of u, we use the spectral method involving Chebyshev differentiation matrixes, defined for the Chebyshev collocation points as follows (see [22]):

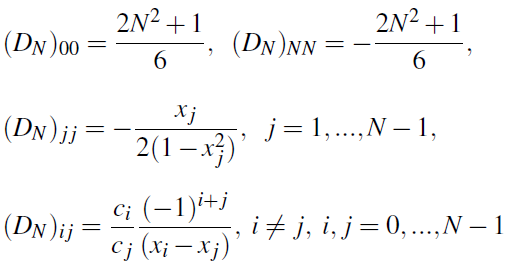
where

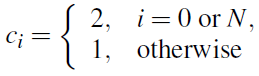
This discretization can be coupled with the discontinuous Galerkin scheme described above, by matching the solution at Chebyshev points, performing the derivative using these points, then returning back to the Legendre points.

Using this method, we compare dispersion (ρ_ω > 0) and dispersionless (ρ_ω = 0) models. We choose a rather high density for the wall in order to underline the difference. The result of the simulation is given below:

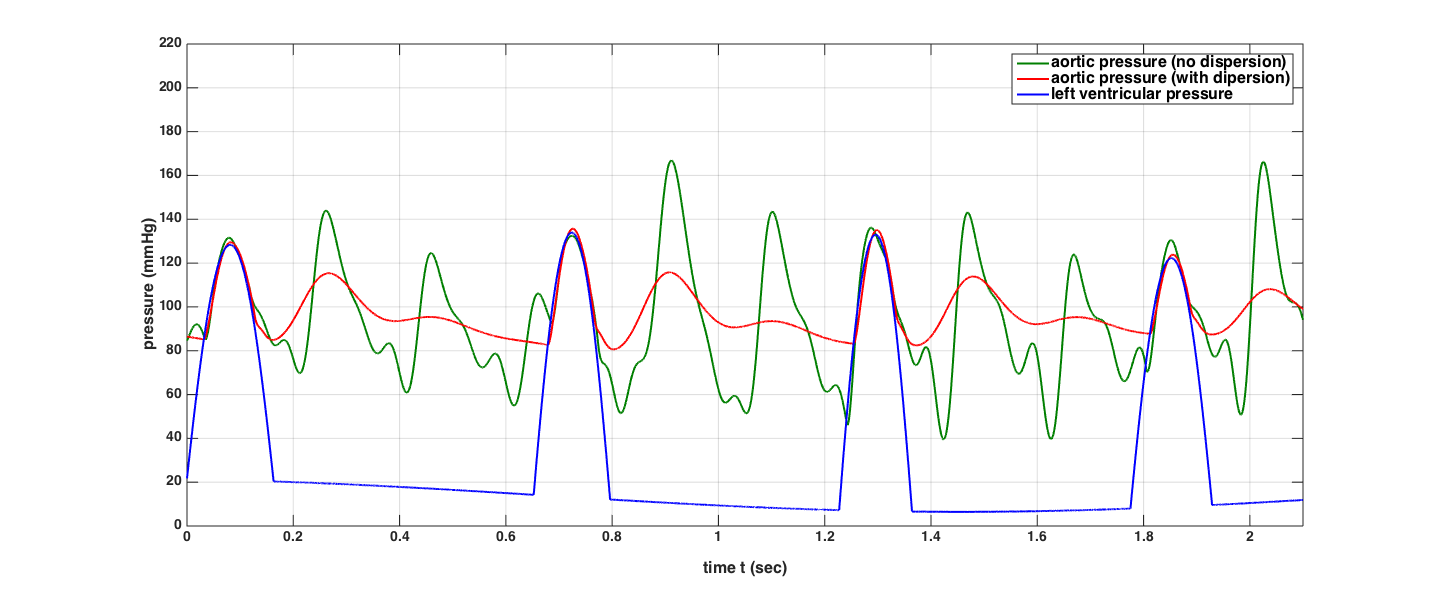
We observe that for the dispersionless case, the multiple peaks between heartbeats indicate that the waves which originate during a systole reflect off the boundaries and travel back and forth (with decreased amplitudes) during the diastole. These can be used to compute the speeds of the pulse waves in relation to the heart rates, similar to [12].

In the dispersive case, the pressure waves have much fewer oscillations than in the dispersionless case. This can be explained by the higher density of the wall, hence higher wall inertia, and consequently fewer transversal oscillations. Since these are temporal recordings at one spatial location, these show an averaging effect due to dispersion of flow along the vessel, and not a dampening of the waves. In simulations we also witnessed a greater degree of the averaging when the wall density increase. If on the other hand we keep all the parameters (e.g. wall density etc) but we consider a shorter length of the vessel M, then by rescaling the spatial variable , one obtains a similar effect - of increasing the value of the wall density, and hence of averaging the pressure pulses originating from the left ventricle. Another effect which can be captured in our numerical model is the variable (along the vessel length) radii and elasticity.

4. Optimization of Mean Arterial Pressure

We now use the numerical model developed so far to perform several optimization tasks, in the same spirit as [4]. The first one is to maintain the mean arterial pressure close to a prescribed reference value (P_ref), in presence of external pressure changes. The external pressure P_ext is taken to vary with time, to mimic the respiratory cycle, according to

Here we consider an arterial segment of length 0.5 m. The following parameter values are used throughout the sequel: μ= 3 x 10^-10 mmHg (viscosity of the blood), ρ = 1050 Kg/m³ (blood density), β = 1418 N/m (elasticity parameter), P_ref = 100 mmHg and the total time of the simulation is t_final = 10 sec.

We are interested in finding the optimal HR (and later also terminal resistance R_t - assumed constant during one heartbeat) which leads to the minimization of the following cost functional

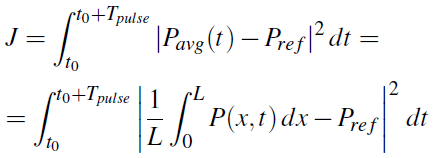
Here the integration is done using an entire heartbeat, with duration T_pulse = 60/HR. The systolic period is taken to be consistently one quarter of T_pulse.

Upon optimization on HR alone, we obtain the following 10-sec recording of the aortic pressure, plotted together with the left ventricular pressure. The first heartbeat has not been included in the plot, since the initial condition is anomalous and does not affect the subsequent dynamics.

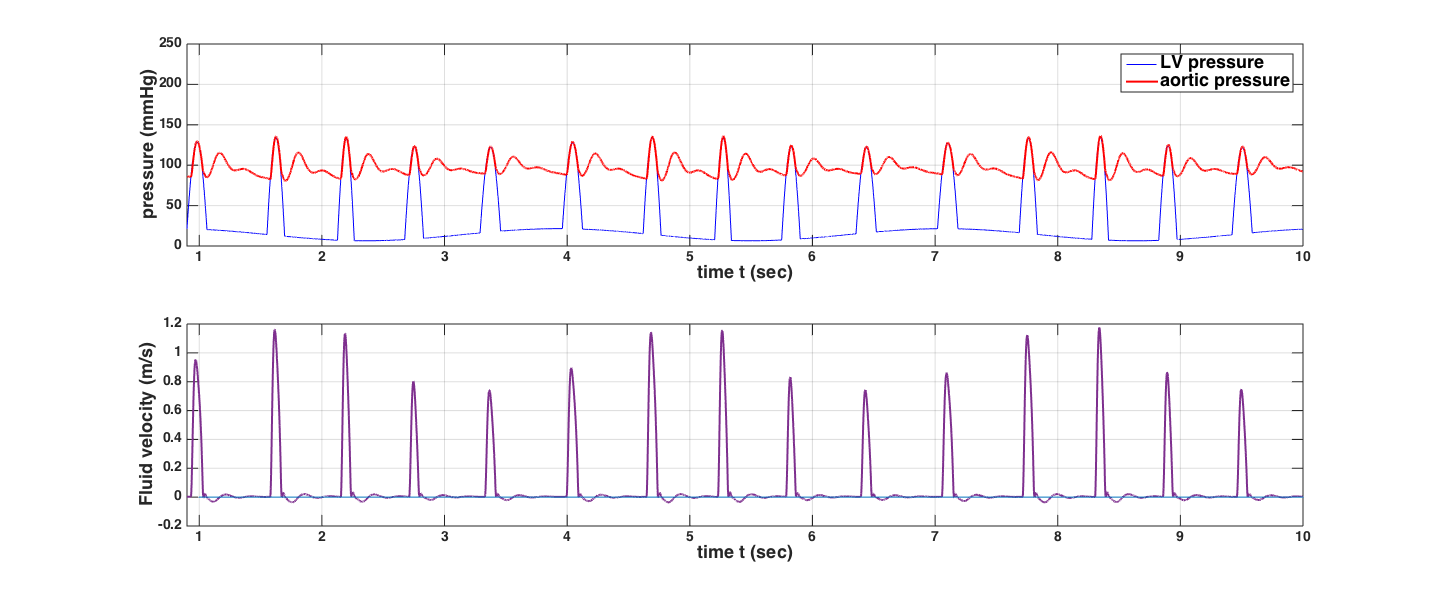
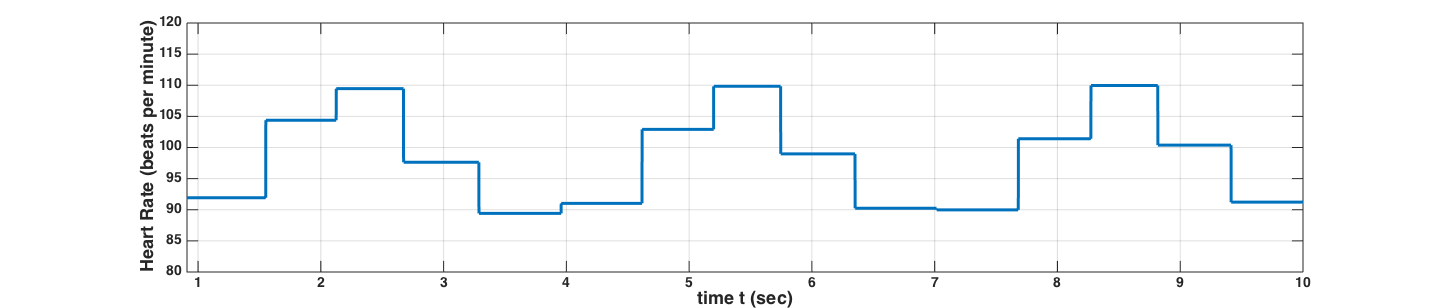
When including the terminal resistance as one of the optimization parameters, we notice a different pattern of the optimal HR, which is to be expected. The variability of the HR and terminal resistance R_t are shown in the figures below:

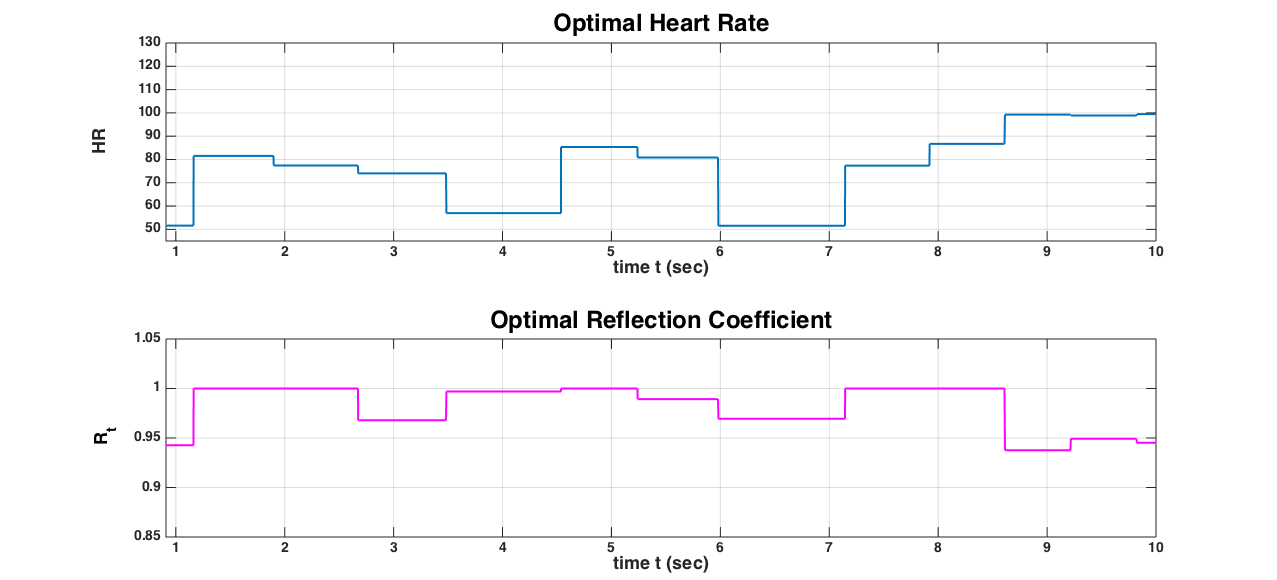
We observe that the terminal resistance R_t is close to 1, which means that there is almost a complete reflection of the characteristic waves and almost complete blockage in the terminal site. HR varies in sync with the respiratory cycle, but the presence of peripheral resistance mechanism is breaking the periodicity of the HR variability, which is what is observed in the real system. Also we note that comparing this range of HR with the results above (when only HR was used in optimization, keeping R_t = 0.9 fixed), leads us to the conclusion that in order to maintain a prescribed mean pressure over one heart beat increasing the R_t (even to its maximal value) is more efficient than increasing the HR. Naturally, the consideration of a single arterial segment (aorta) avoids the effects of the complexity of the vascular network, which would add additional irregular behavior in the HR variability.

5. Optimal Control of Mean Arterial Pressure

We consider the optimal control problem of achieving a prescribed mean arterial pressure by allowing for variable terminal resistance R_t = R during the time period [t₀, t₀ + T_pulse] of one heart beat, T_pulse = 60/HR. Note that we do not perform optimization on the heart rate HR, since the HR can be controlled separately.

For simplicity, we formulate our optimal control problem using the dispersionless system:

and write it as an initial value problem in the Hilbert space :

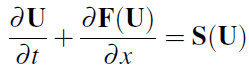
where and A_y is an unbounded operator on X:

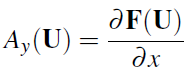
with domain

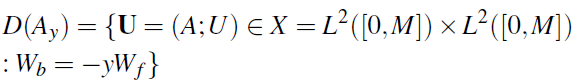
encodes the boundary conditions in terms of the control variable y (expressed as boundary control). In our application y = R_t is the terminal reflection coefficient which is allowed to vary during the time period of one heart beat T = 60/HR.

The optimization task is defined as follows: determine the optimal terminal resistance that achieves the desired mean pressure. This is a nontrivial fact, since we assume the external pressure is variable (possibly due to a sudden drop or rise in pressure,) the system tries to find the optimal value of the Heart Rate that achieves the desired goal.

The optimal control problem is to find y = y(t) that minimizes the integral

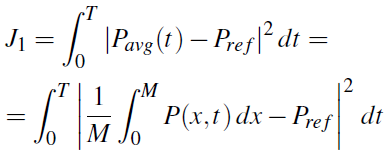
Due to the non-standard nature of the Dirichlet boundary control problem posed, we expect that the full PDE boundary control will lead to an adjoint formulation of the optimal control problem involving integral formulation of the necessary condition for optimality (see [13]). This will be pursued elsewhere. In the sequel we turn to a pseudo spectral discretization of the optimal control problem [15], [19]. The discretization uses the same framework as the numerical scheme already discussed, using Legendre polynomials and Legendre Gauss nodes. For simplicity, we describe this discretization procedure on an optimal control problem for the Dirichlet boundary control for the viscous Burgers equation:

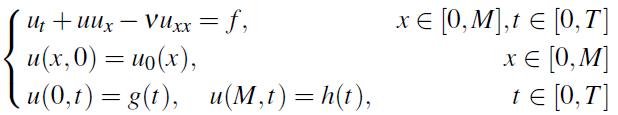
with g and h the controls, and cost functional to be minimized

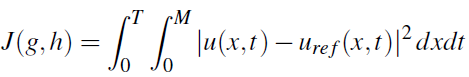
where u_ref is a reference (desired) profile for the solution.

We choose the Legendre-Gauss-Lobatto (LGL) points , (cf. [19]), where x₁,...x_N-1are the zeros of L^'_N, the derivatives of the Legendre polynomial of degree N and we approximate the function u using the Lagrange interpolant for the points (x_j,u(x_j)). Then we introduce the approximate solution:

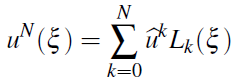
and convert the optimal PDE control problem to the optimal ODE control problem:

Minimize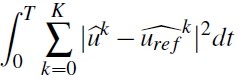


subject to

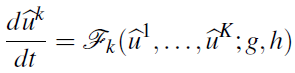
Here the right-hand side is obtained from the variational formulation of the PDE:

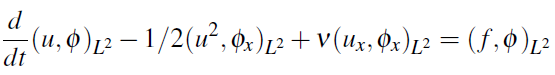
If we restrict the test functions to polynomials of degree N or less, then we obtain

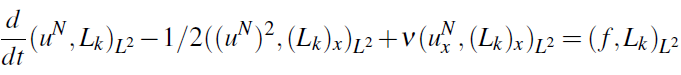
or

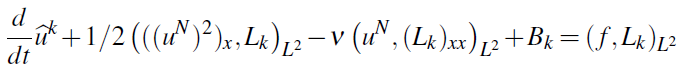
Here the boundary contribution is

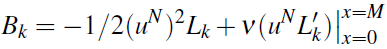
This leads to the expression for the right hand side in (16):
.
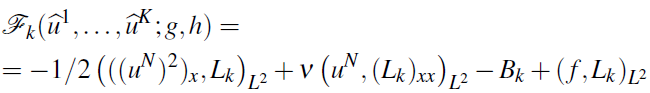Note that B_k can be written in terms of the boundary control as:
.

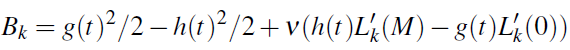Applying Pontryagin minimum principle we are led to an adjoint problem for the adjoint variables λ^k, k = 0,...K.

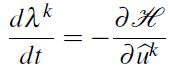
where

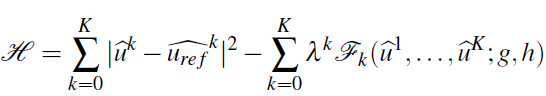
is the Hamiltonian. A necessary optimal condition is then
, for each fixed time t, which yields the optimal values and .

A similar construction can be carried out for the inviscid Euler system (15), which yields, upon discretization using the same Gauss Legendre Lobatto points, the system

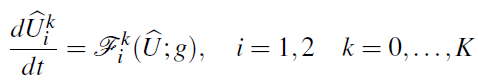
The adjoint system takes the form

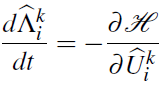
where the Hamiltonian function is

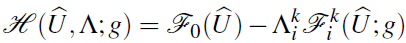
Applying of the Pontryagin minimum principle leads to the computation of the optimal . We remark that while this is a nonstandard application of the Pontryagin minimum principle, it follows the same steps as the traditional principle where pure Dirichlet boundary conditions are involved. A numerical implementation of this discretized control problem as well as a more detailed discussion on the connection with the full PDE boundary control will be reported elsewhere.

6. Conclusions

The numerical optimization results presented here are relevant for understanding how boundary control affects the dynamics of the pressure and flow in an arterial segment, via the valve model at the root of the vascular network and via peripheral resistance model at the outflow. The consideration of a single edge can be viewed as certainly restrictive from a physiological point of view, but can help in further studies where the entire vascular network is considered. Furthermore, more realistic models for the rheology of blood, for the mechanical characteristics of the tube walls and for the fluid-structure interactions are worthy to be incorporated in the optimization studies presented here, something we intend to report elsewhere.

Acknowledgement

R.C. was supported by a grant from the UCCS BioFrontiers Center of the University of Colorado. R.C. is also grateful for the hospitality of the Universit`a degli Studi di Salerno during his stay there.

References