Journal of Fluid Flow, Heat and Mass Transfer (JFFHMT)

ISSN: 2368-6111

Nomenclature

• C_P: Specific Heat, [J/kg.K]
• d_h: Hydraulic diameter, [m]
• h: Heat transfer Coefficient, [W/m².K]
• k: Thermal conductivity, [W/m.K]
• Nu: Nusselt number, [-]
• Q: Heat flux, [W/m²]
• R: Radius, [m]
• Re: Reynolds number, [-]
• T: Temperature, [K]

Greek Symbols

• φ: Nanoparticle Volumetric Concentration, [%]
• µ: Dynamic Viscosity, [kg/m.s]
• ρ: Density, [kg/m³]

Subscripts

• bf: Base fluid
• i: Inlet, inner
• nf: Nanofluid
• o: Outlet, outer
• p: Particle
• w: Wall

1. Introduction

Heat transfer by convection is very important for many industrial heating and cooling applications. The heat convection can passively be enhanced by changing flow geometry, boundary conditions or by enhancing fluid thermophysical properties. With presenting the concept of nanofluid (Choi, 1995), it attracted the attention of many researchers who were interested in increasing the heat transfer coefficient of liquids in many industrial applications.

They show that use of nanofluids does enhance heat transfer coefficient for heat transfer applications. Such enhancement mainly depends upon factors such as the shape of particles, the dimensions of particles, the volume fractions of particles in the suspensions, and the thermal properties of particle materials.

Pak et al., 1998; Qiang et al., 2002; Xuan et al., 2003; Yang et al., 2005; Heris et al., 2007; Nguyena et al., 2007; VELAGAPUDI et al., 2008; Duangthongsuk et al., 2010; Nasiri et al., 2011; Murugesan et al., 2012; Darzi et al., 2013; Nield et al., 2014 have investigated the convective heat transfer of nanofluids. They show that use of nanofluids does enhance heat transfer coefficient for heat transfer applications. Such enhancement mainly depends upon factors such as the shape of particles, the dimensions of particles, the volume fractions of particles in the suspensions, and the thermal properties of particle materials.

Pak and Cho (Pak et al., 1998) published a correlation for the turbulent connective heat transfer for dilute dispersed fluids with submicron metallic oxide particles which is given by the following equation:

While Xuan and Li (Xuan et al., 2003) correlate Nusslet number for both laminar and turbulent flow as follows;

(Qiang et al., 2002) highlighted that the conventional convective heat transfer correlation of the pure fluid is not applicable to the nanofluid and recommended the correlation for Nusslet number for convective heat transfer with nanofluid flows in Equations (2) and (3).

(VELAGAPUDI et al., 2008) recommend a new correlations (4) and (5) for water-Al₂O₃ and water-CuO when the flow is turbulent;

(Bianco et al., 2009) concluded that single phase and two phase methods revealed approximated results, especially in the case of using temperature dependent properties. Demir (Demir et al., 2011) mentioned that although the nanofluid is actually a two-phase fluid in nature, the results show that the nanofluid behaves more like a pure fluid than a liquid-solid mixture. Kumar (Kumar, 2011) after validation his numerical study with experimental works, he emphasized single phase approach does not predict heat transfer coefficient as accurately as in the turbulent regime.

(Maїga et al., 2005) studied forced convection flow of water-Al₂O₃ and ethylene glycol-Al₂O₃ nanofluids inside a uniformly heated tube at the wall and a system of parallel, coaxial for both laminar and turbulent flow. Numerical results showed better heat transfer enhancement. Finally, he recommends with a correlation (Maїga et al., 2006) to estimate Nu, Equation (6).

(Namburu et al., 2009) found in his numerical analysis for different nanofluids (CuO, Al₂O₃ and SiO₂) in ethylene glycol and water mixture flowing through a circular tube under constant heat flux condition that Gnielinski correlation can be used in determining the Nusselt number with volume concentration up to 6%.

(Sharifi et al., 2012) examined the heat transfer coefficient for laminar flow inside tube subjected to constant heat flux with a concentration ratio from 1 to 10% by experimental and numerical methods. Good agreement was achieved between both methods and increase of heat transfer coefficient of about 60%.

Most numerical researches in convection heat transfer for nanofluids flow were in a cylindrical shape, (Rostamani et al., 2010) in rectangular duct, (Manca et al., 2012) in a triangular cross sectioned, (Bhattacharya et al., 2009) in rectangular micro-channel, (Pathipakka et al., 2010) in a circular tube fitted with helical twist inserts, (Vajjha et al., 2010) in flat tubes of the radiator and (Manca et al., 2012) in a ribbed channel and square cross section tubes. While others considered the natural convection for annular enclosures (Cianfrini et al., 2011; Abouali et al., 2012) and horizontal tube (Rashmi et al., 2011).

Turbulent flows are significantly affected by the existence of walls, where the areas that described by viscosity-affected areas have large gradients in the solution variables and accurate presentation of the near-wall region determines successful prediction of wall bounded turbulent flows. (Gerasimov, 2006) proposed in his seminar a strategy of computed wall y+ that dealing with near-wall turbulent flows using Fluent from ANSYS. This technique eliminates the traditional step of what is termed the grid independence test that requires a lot of time and computational effort. This strategy assists in selecting the most suitable near-wall treatment (wall functions or near-wall modeling) and the corresponding turbulence model based on the wall y+ (Salim et al., 2009).

The aim of this paper is to investigate numerically the application of YPlus strategy in heat transfer characteristics for Al₂O₃/water and TiO₂/water flow through an annulus by applying two turbulence models of k-e and Spalart-Allmaras (S-A), evaluating its performance and assessment of the results with the proposed correlations.

2. Mathematical Formulation

2. 1. Problem Statement

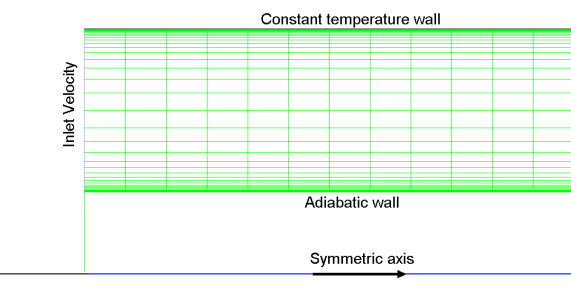
The geometry of the annular channel has an outer diameter, inner diameter and length of 30, 10 and 1500 mm, respectively. This geometry is represented by a two-dimensional rectangular duct of height h (difference between outer and inner diameter) and length l. The tube has an appropriate length in order to obtain fully developed profiles (velocity and thermal) at the outlet section (L/D_h > 10), (Incropera et al., 2007). The outer wall is subjected to a constant wall temperature. The nanofluid enters the duct with uniform velocity and temperature and is affected only by the duct conditions. The nanofluid is incompressible and the flow is turbulent.

Also, it is assumed that the liquid and solid are in thermal equilibrium and they flow at same velocity. The resultant mixture may be considered as a conventional single phase fluid. The assumption of single phase for a nanofluid is validated to an extent by (Choi et al., 2001; Bianco et al., 2009; Demir et al., 2011; Kumar, 2011). Model is constructed and discretized using the strategy of computed wall y+ that is recommended when dealing with such flows as proposed by Gerasimov in using Fluent from ANSYS (Gerasimov, 2006). This strategy assists in selecting the most suitable near-wall treatment (wall functions or near-wall modeling) and the corresponding turbulence model based on the wall y+ (Salim et al., 2009).

The CFD commercial code, Fluent, is employed to solve the problem by means of finite volume method. Two turbulence model namely k-e and Spalart-Allmaras (S-A) are implemented. Spalart-Allmaras model is the most popular one-equation model. This model has been shown to give acceptable results for a wide variety of situations and is known for its stability. The numerical simulation results are also compared with correlations found by (Pak et al., 1998, Xuan et al., 2003, Maїga et al., 2006, and VELAGAPUDI et al., 2008). To save computational time, half of the domain is selected as the computational domain since the problem is Axi-symmetric (Fig. 1).

2. 2. Governing equations

The single-phase model, which has been used frequently for nanofluids, is also implemented to compare its predictions with the mixture model. The following equations represent the mathematical formulation of the single-phase model by (Choi et al., 2001; Bianco et al., 2009; Demir et al., 2011; Kumar, 2011):

Conservation of mass:

Momentum equation:

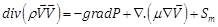
Energy equation:

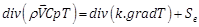
The compression work and the viscous dissipation are assumed negligible in the energy equation; the source/sink terms S_m and S_e represent the integrated effects of momentum and energy exchange with base fluid, as shown in the following, and they are equal to zero in the case of single-phase model.

The previous equations can be solved with the following boundary conditions;

At outer wall:

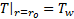
At inner wall

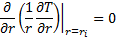
2. 3. Thermophysical Properties of Nanofluid

In the absence of experimental data for nanofluid densities, constant value temperature independent values, based on nanoparticle volume fraction, the following parameters were used as reported by (Pak et al., 1998; Maїga et al., 2004; Roy et al., 2004) and others.

Density:

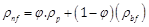
Specific heat:

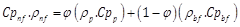
Effective thermal conductivity:

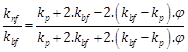
Viscosity

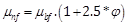
where, µ_bf, Cp_nf, Cp_bf, Cp_p, r_p, k_bf, k_p, and ϕ are basefluid viscosity, nanofluid heat capacity, base fluid heat capacity, nanoparticles heat capacity, nanoparticles density, thermal conductivity of base fluid, thermal conductivity of nanoparticles, and volume fraction of nanoparticles respectively.

The results of (Duangthongsuk et al., 2010) showed that use of the viscosity models to describe the Nusselt number of nanofluids gives different values compared with use of the measured data, by about 2-3%.

Specifications of nanoparticles used in this study are available in Table 1.

Table 1. Nanoparticles specifications.

Particle	Size (nm)	r (kg/m3)	k (W/m.K)	Cp (J/kg.K)
Al2O3	25	3970	46	750
TiO2	10	3840	11.7	710

2. 4. Data Analysis

Heat transfer (q") between nanofluid and outer wall is obtained through the following equation:

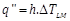
Where DT_LM is mean logarithmic temperature deference and is defined by:

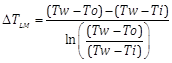
In order to calculate Reynolds number (Re), Nusselt number (Nu) and Peclet number (Pe) for annular tube, hydraulic diameter (d_h) of the channel is used.

Where d_h is hydraulic diameter and calculated by:

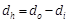
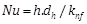
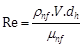
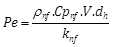
Where d_o, d_i is the outer and inner diameter of the annular passage. K_nf, r_nf, V and µ_nf are thermal conductivity, density, velocity, and viscosity of nanofluid respectively.

3. Results and Discussions

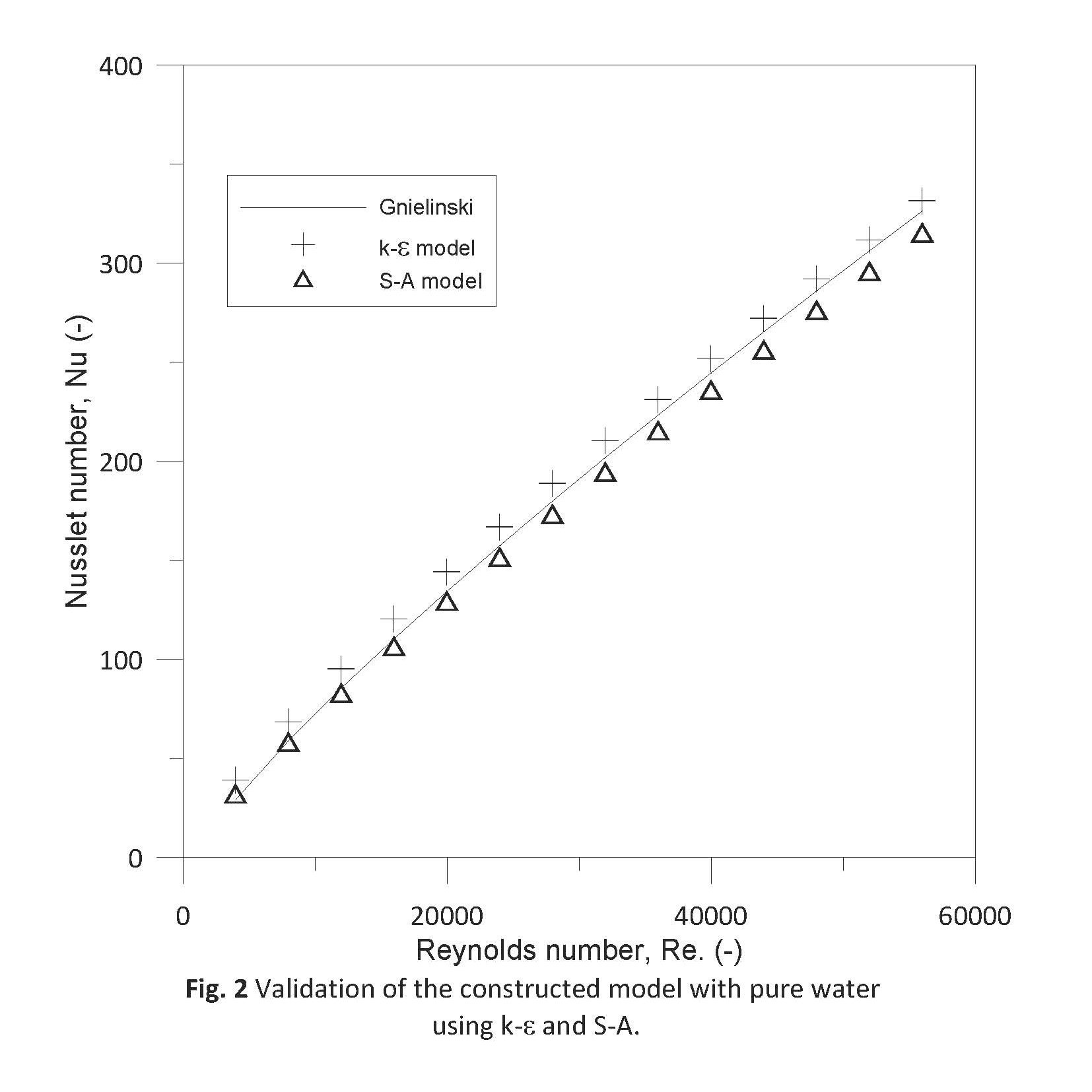
The results of this investigation obtained for distilled water for both k-Ɛ and S-A turbulence models were compared with famous equation of Gnielinski (Incropera et al., 2007) as shown in Fig. 2. It is clear to note that S-A model and k-Ɛ models exhibited good agreement with Gnielinski equation with a maximum deviation of 6% for a S-A model rather than k-Ɛ model which revealed 34% maximum error decreased with increasing Re to reach 2% in the end of the range (about Re = 56000).

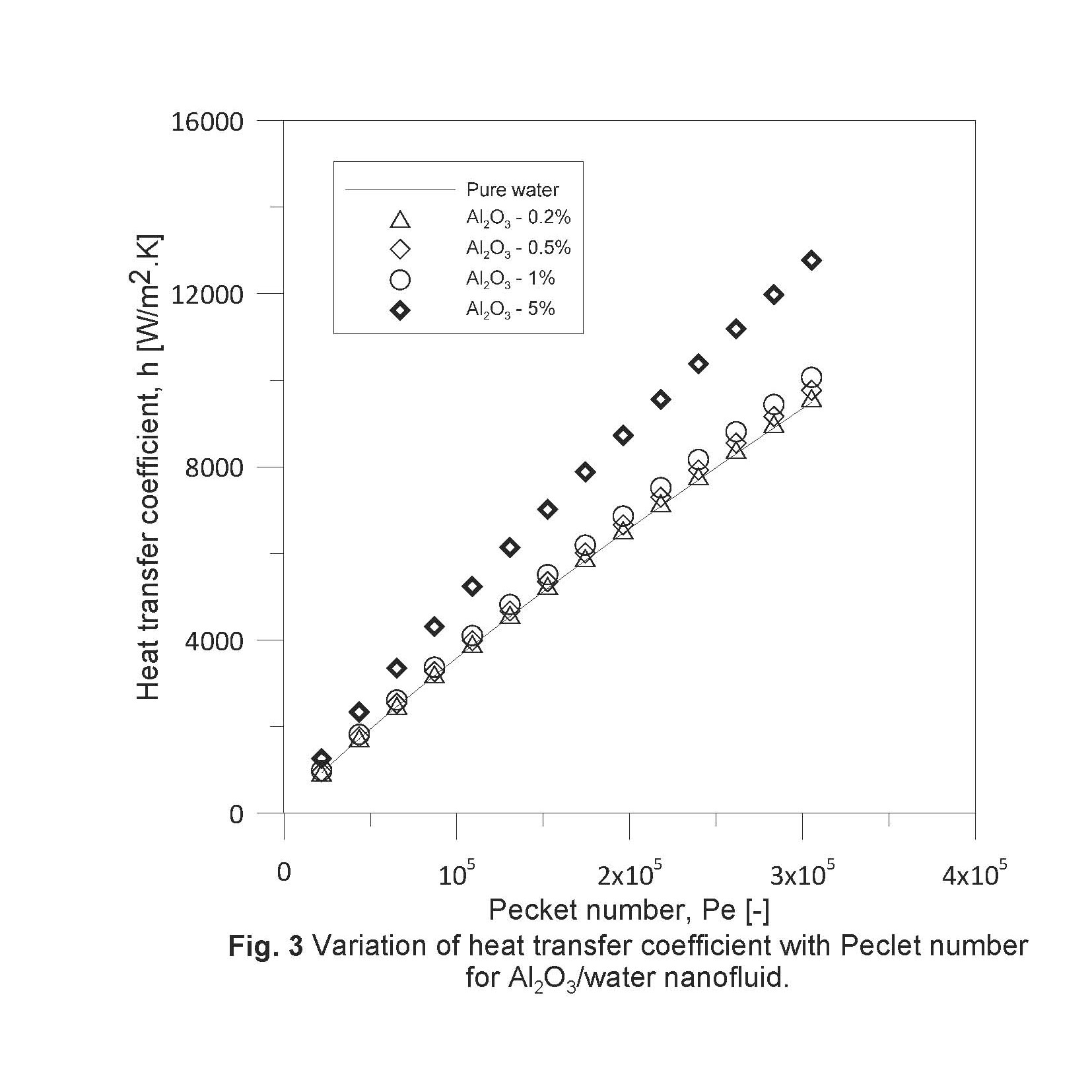
The study were conducted for volumetric concentrations of 0.2, 0.5, 1.0 and 5% of Al₂O₃ and TiO₂ nanoparticles. The convection heat transfer coefficient related to Al₂O₃/water nanofluid versus Peclet number is presented through Fig. 3. The Peclet number (Pe) is a comprehensive parameter to describe such effects, (Xuan et al., 2000).

Based on the results, for definite Peclet number, the convective heat transfer coefficient (h) of nanofluid is higher than that of base fluid. This enhancement considerably is dependent on the concentration of nanoparticles. For example at Peclet number about 21,800, the heat transfer coefficients are 6.4% and 36.1% greater than those of the base fluid when the nanoparticle concentration are 1.0 vol.% and 5.0 vol.% respectively.

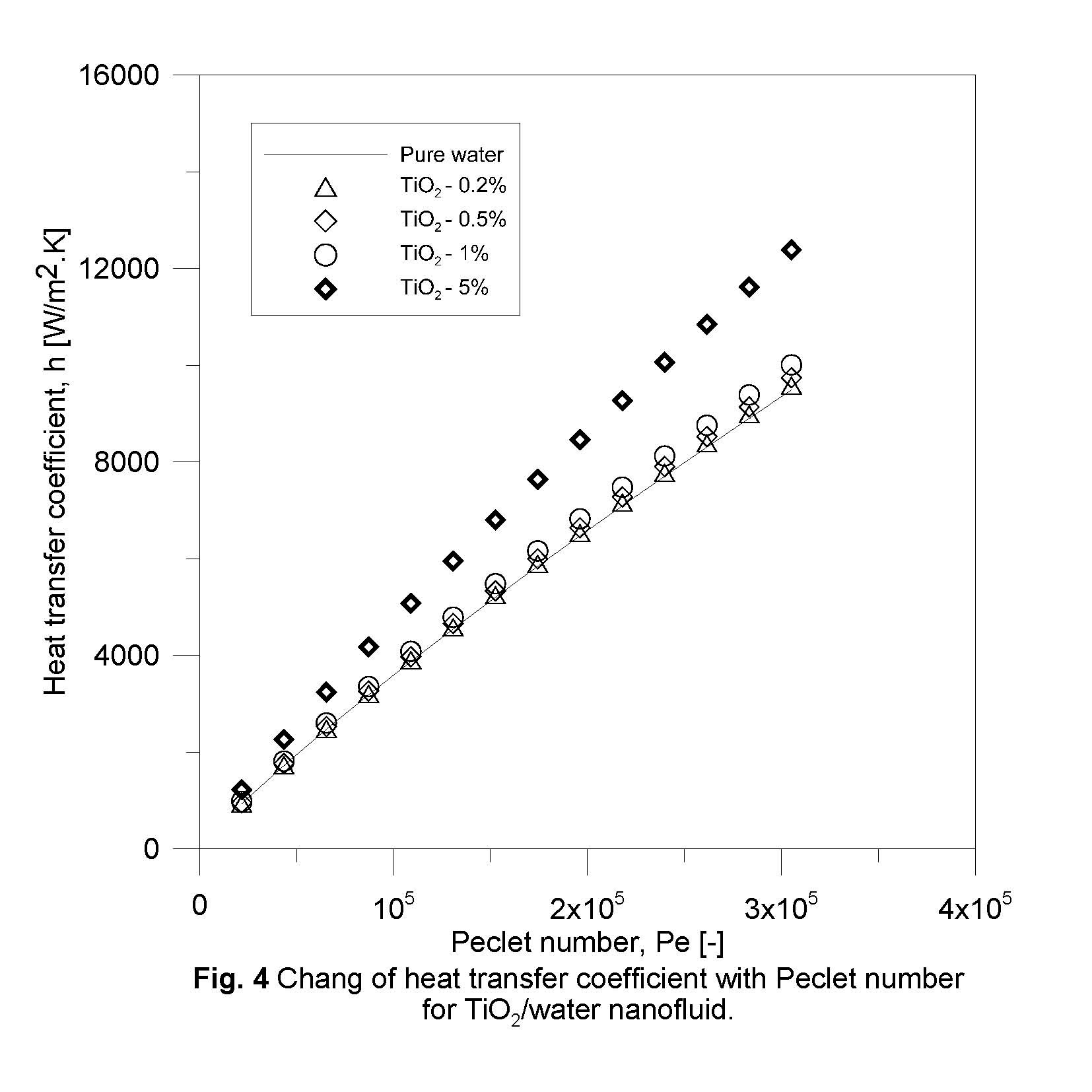
The results related to TiO₂/water nanofluid are demonstrated through Fig. 4. The behavior of this nanofluid is similar to that of Al₂O₃/water. For example the enhancements of heat transfer coefficient for TiO₂/water nanofluid at Peclet number about 21,800 are about 5.7% and 31.7% for nanoparticle concentrations of 1.0 vol. % and 5.0 vol. % respectively.

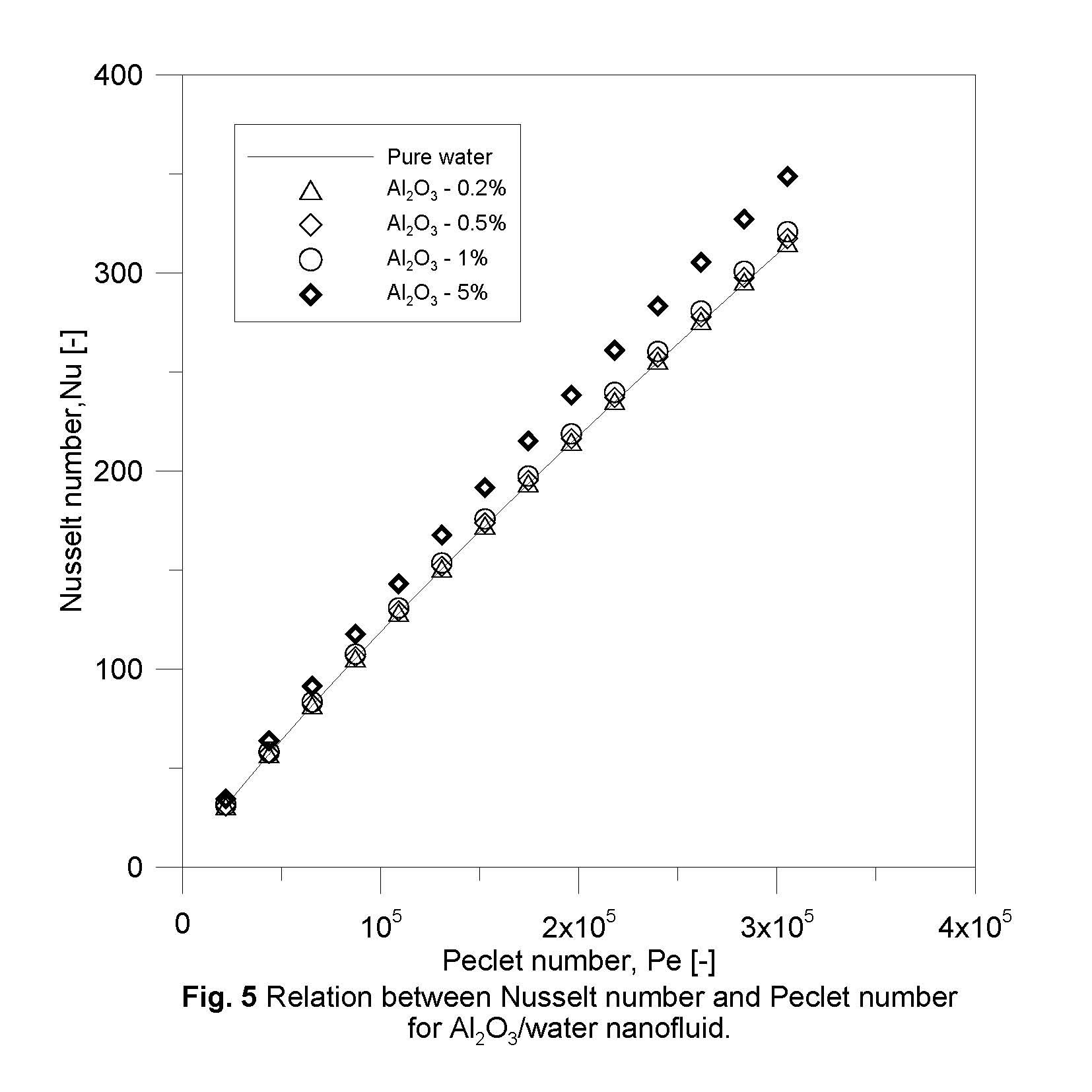
Figures 5 and 6 demonstrate the Nusselt number for Al₂O₃/water and TiO₂/water nanofluids for different Peclet numbers. Both nanofluids show higher Nusselt number than those of the base fluids and enhancement increases with nanoparticle concentration. For example at Peclet number about 21,800, the enhancement of Nusselt number for Al₂O₃/water nanofluid with nanoparticles concentrations of 0.2, 0.5, 1.0 and 5.0% are 0.48%, 1.1%, 2.2% and 11.1% respectively.

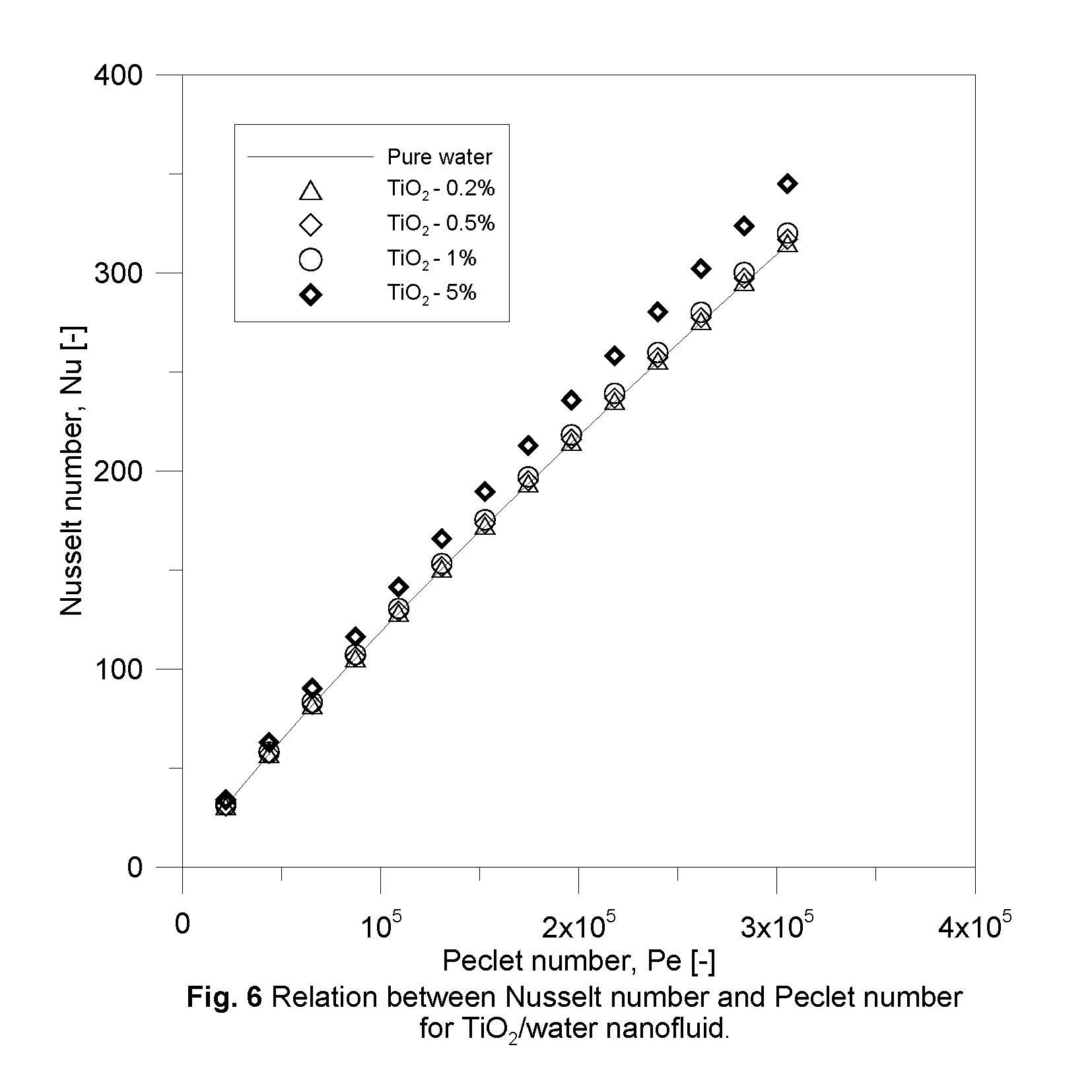
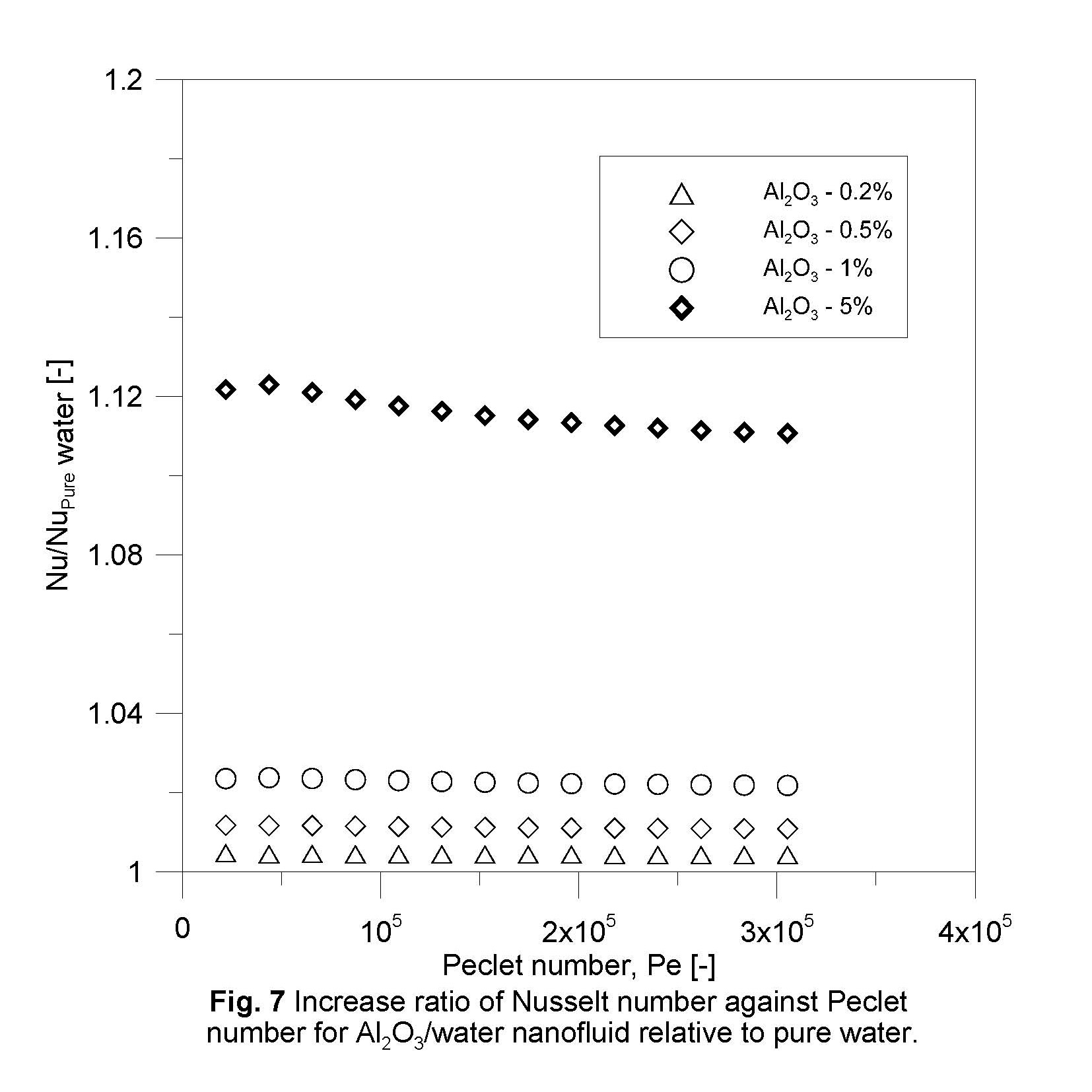
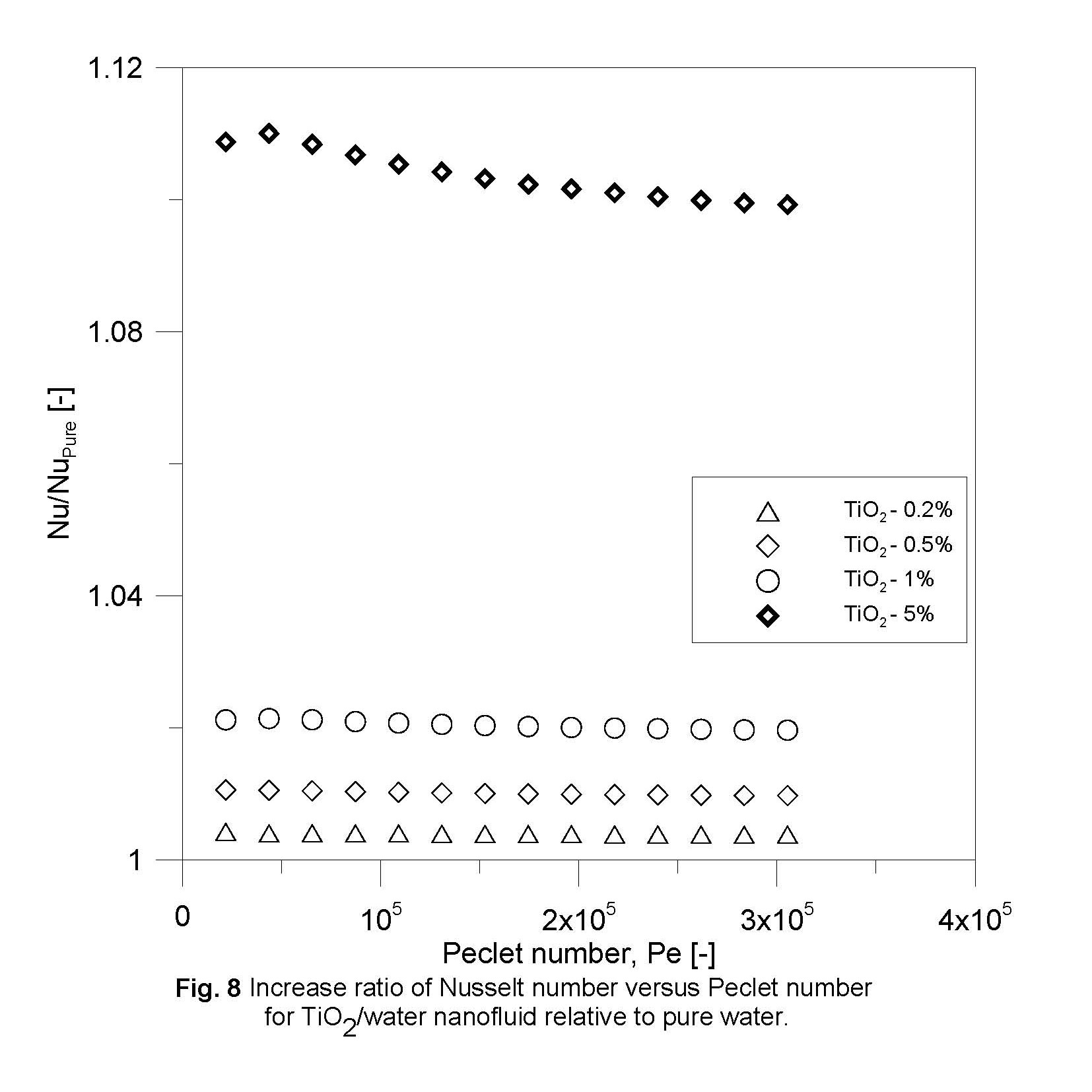
For TiO₂/water nanofluid at Peclet number about 21,800, the increment of Nusselt number for TiO₂ nanoparticle concentrations of 0.1, 0.5, 1.0 and 1.5% are 0.43%, 1.0 %, 2.1% and 10.8 % respectively. It is be noted that for both nanofluids, there is no significant enhancement in Nusselt number for concentrations less than 0.2%, which noted by (Kumar, 2011). Moreover, the relative enhancement of heat transfer is remarkably not affected by change of Peclet number (Pe) as observed in Figs. 7 and 8.

Such improvement of heat transfer becomes more pronounced with the increase of the particle concentration. The reduction of the thermal boundary layer thickness due to the presence of particles and their random motion within the base fluid may have important contributions to such heat transfer improvement as well.

The heat transfer enhancement of nanofluids has been reported for annular channel. (Nasiri et al., 2011) presented the experimental results for Al₂O₃/water nanofluid with concentrations of 0.5% and 1% at Peclet number about 59,000 under turbulent regime in annular circular tube and showed the increments of Nusselt number were 6.2 % and 13.6% respectively. The corresponding results, for the present study, at the same Peclet number and nanoparticle concentrations are 1.1%, 2.3%.

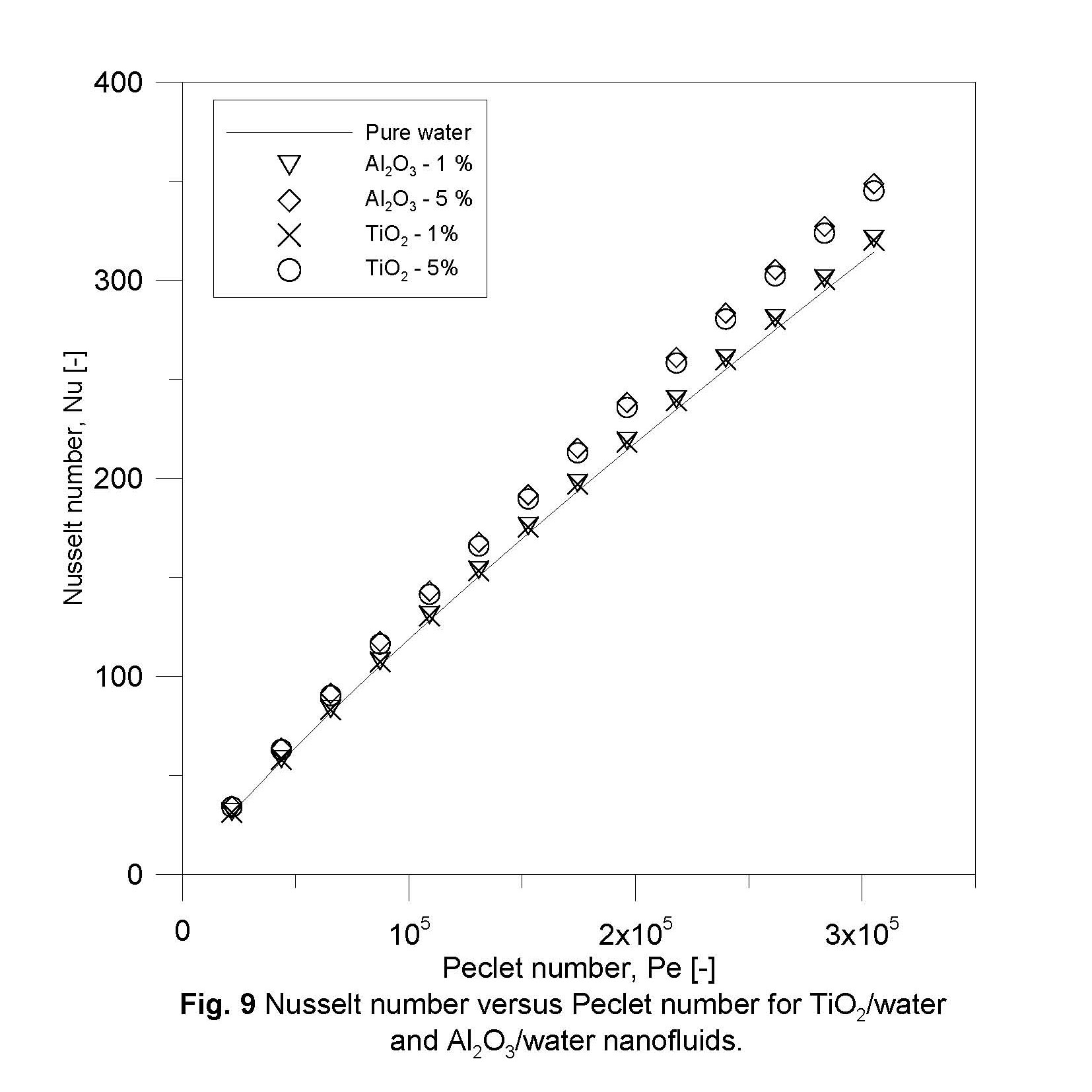
In order to compare the performance of two employed nanofluids in this research, Nusselt number plotted for concentrations of 1.0 and 5.0% in Fig. 9. Based on the results of this figure, there is no significant difference between the Nusselt numbers of two employed nanofluids.

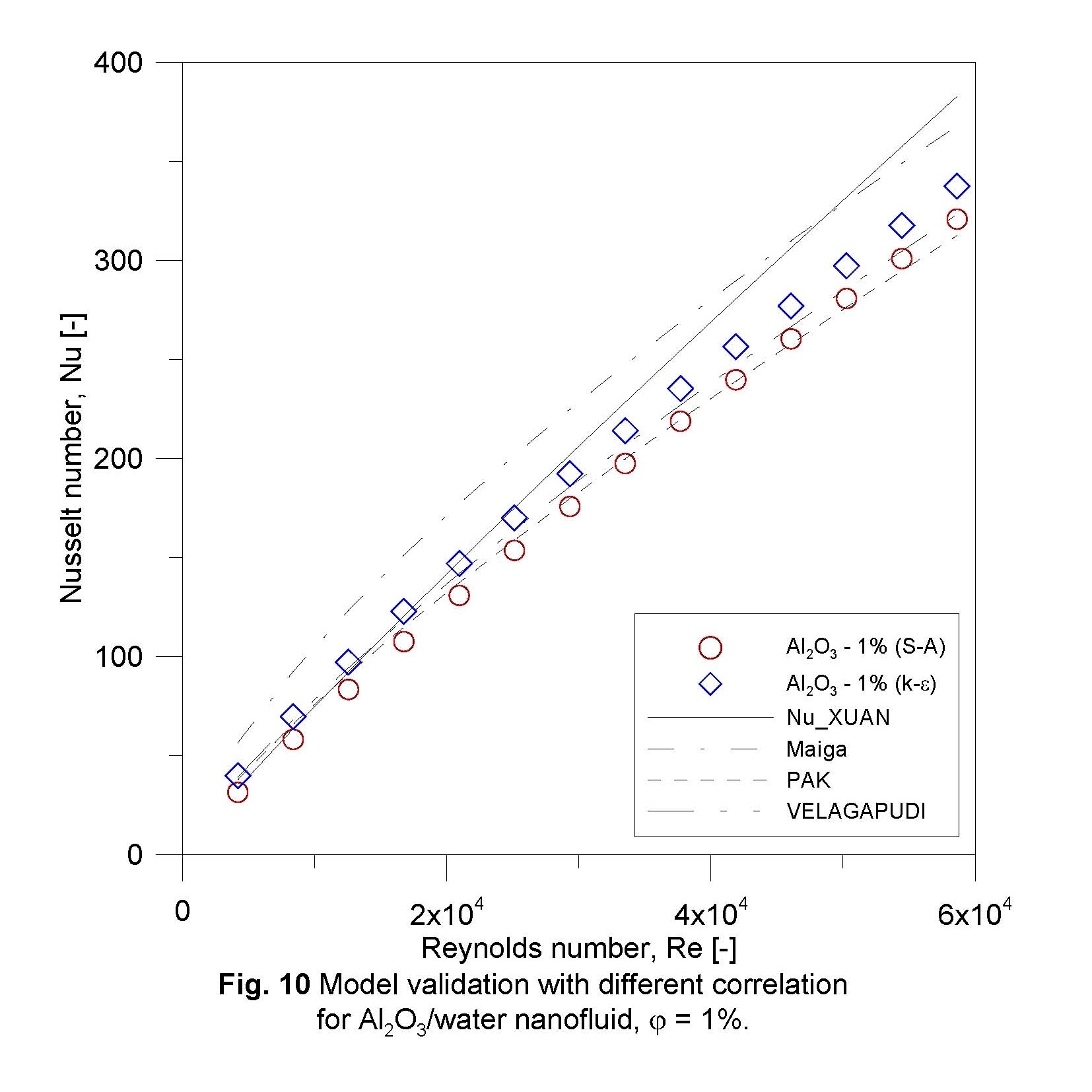
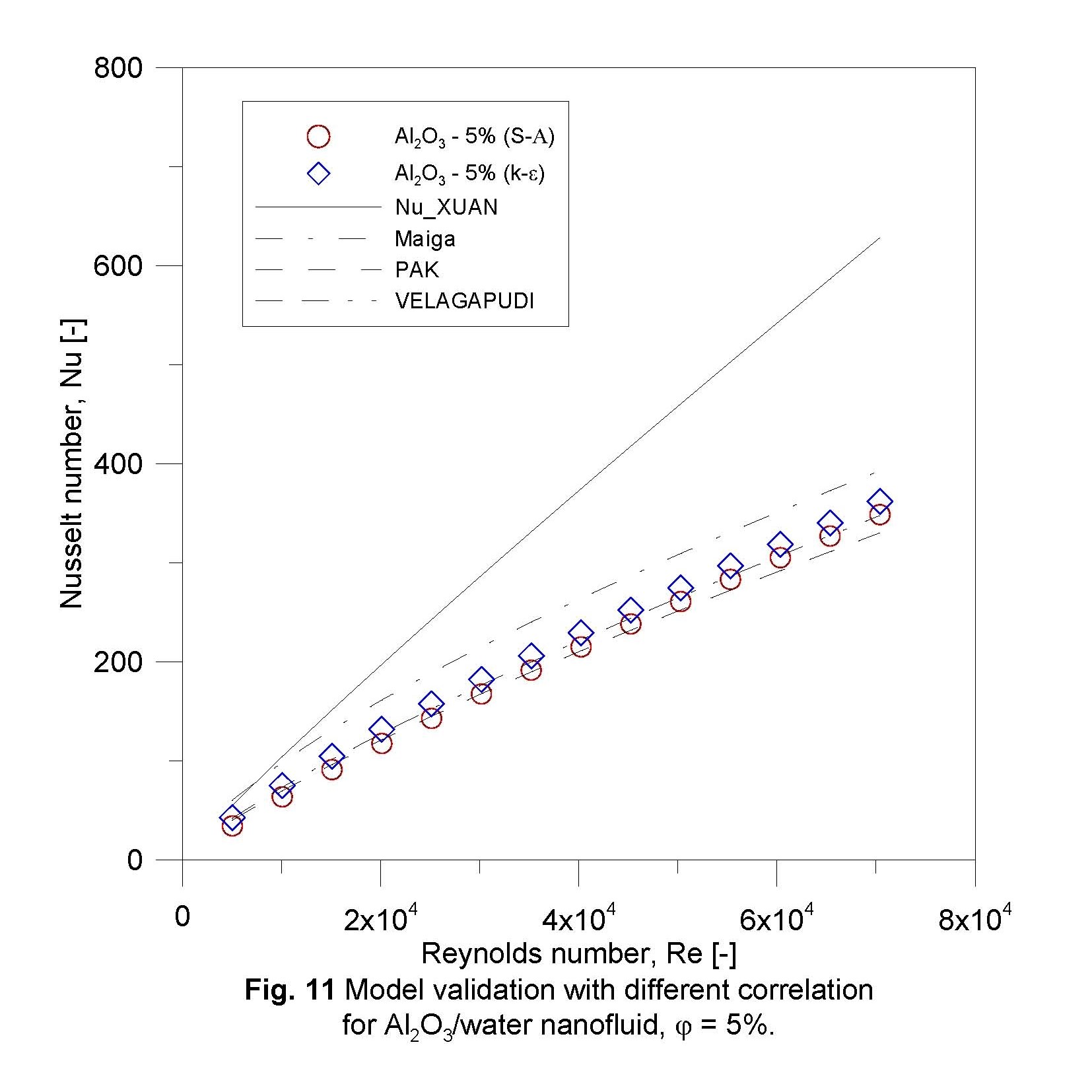
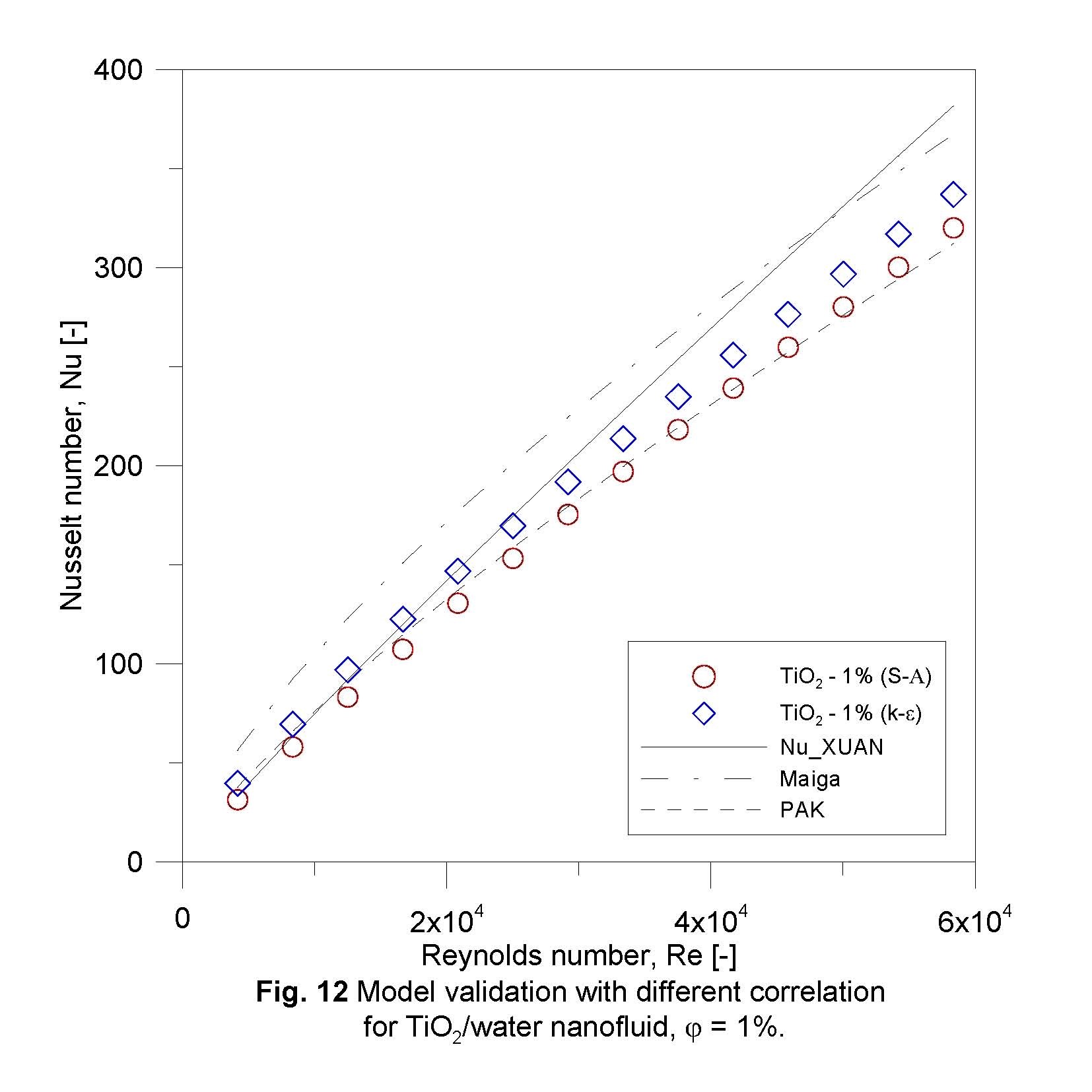
Validation of results with correlations found by (Pak et al., 1998; Xuan et al., 2003; Maїga et al., 2006; VELAGAPUDI et al., 2008) are presented for concentrations of 1.0 and 5.0% for both nanofluids. Validation with the correlations was also done with both results obtained by k-Ɛ and S-A turbulence models. Figures 10 and 11 are the validation for Al₂O₃/water for concentrations of 1.0 % and 5.0%, respectively. It is obvious that correlations of (Pak et al., 1998) and (VELAGAPUDI et al., 2008) are best fitted with results of S-A model with maximum error of 2%, while (Maїga et al., 2006) has overestimated results, (Xuan et al., 2003) has diversion that gets growing with increasing Re. Validation of (Pak et al., 1998) correlation also emphasized to give better results for comparison by (Bianco et al., 2011) for single phase fluid.

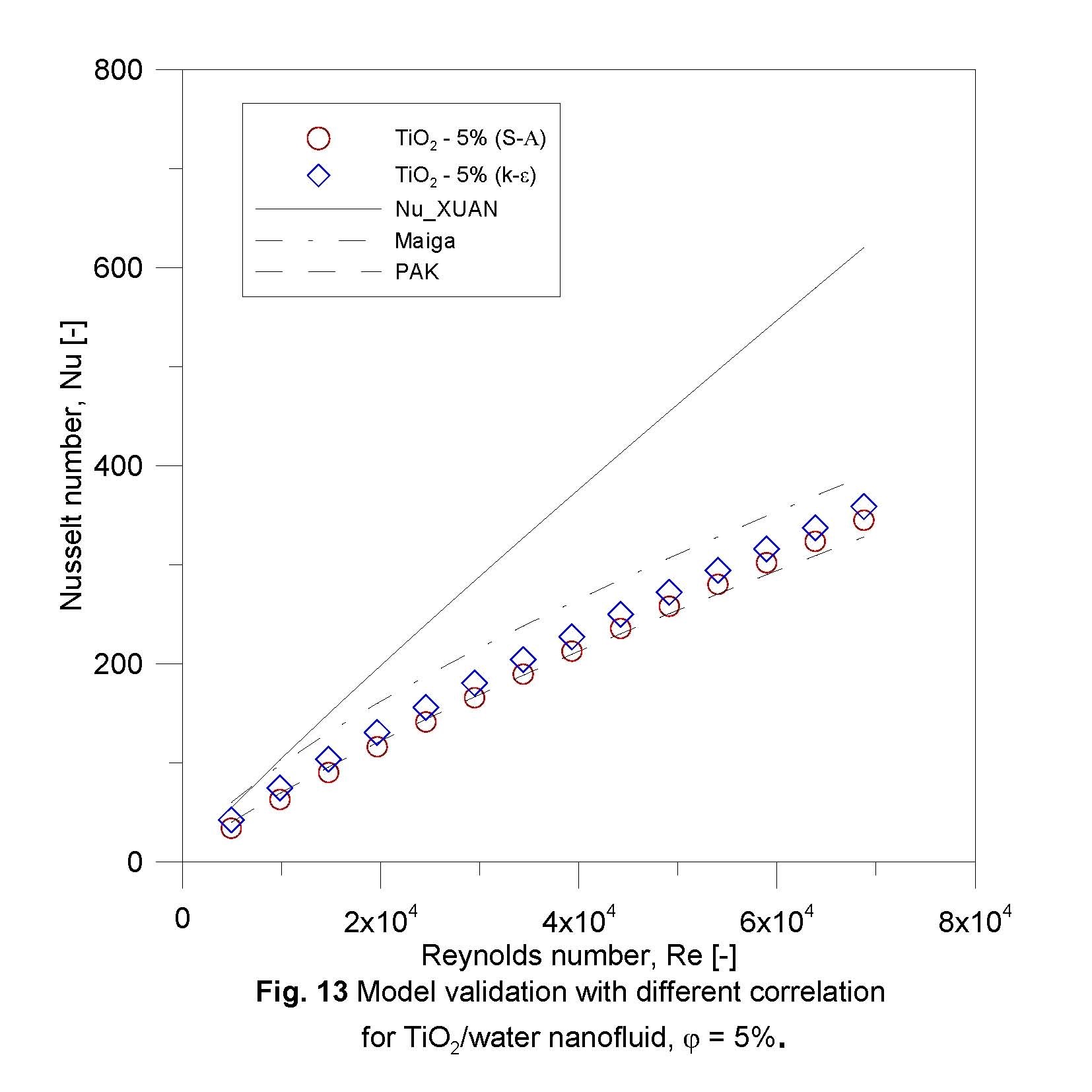
Similar trends can be found for TiO₂/water validation Figs. 12 and 13. No correlation from (VELAGAPUDI et al., 2008) for TiO₂/water nanofluid.

4. Conclusion

Numerical investigation for heat transfer enhancement for flow inside annular tube was done using two turbulence models, k-Ɛ and S-A. A grid was constructed with condition that y+ is always below 1. The following concluded;

• Spalart-Allmaras turbulence model gives better convergence and more stability throughout validation with pure water flow.
• Heat transfer coefficient does enhanced by increasing concentration ratio of nanoparticles for each Al₂O₃ and TiO₂.

Although (Pak et al., 1998) correlation is the eldest correlation, however, it gives best results when dealing nanofluid as single phase fluid.

References