Volume 2 - Year 2015 - Pages 40-46
DOI: 10.11159/jffhmt.2015.006
Heat Transfer Modeling of Bipropellant Thrusters for using in Multidisciplinary Design Optimization Algorithm
A. Adami1, M. Mortazavi1, M. Nosratollahi2
1Amirkabir
University of Technology, Tehran, Iran
Aha.aerospace@aut.ac.ir; mortazavi@aut.ac.ir
2Malek e Ashtar
University of Technology, Tehran, Iran
M_nosratollahi@sbu.ac.ir
Abstract - Modern designing methods such as multidisciplinary design optimization (MDO) need semi-accurate model of each discipline in preliminary design phase to analyze many configurations in a shorter elapsed time. One of the most important disciplines in multidisciplinary design optimization of bipropellant is thermal-control and cooling. Every cooling method such as regenerative, film and radiative cooling needs to predict heat transfer from combustion chamber. All known relations for determination of the convective heat transfer coefficient require many parameters especially wall temperatures, which is not accessible before cooling. Using such relations lead to implicit solutions and time consuming. In this paper, engineering model of heat transfer from combustion chamber is introduced for using in multidisciplinary design optimization. The presented algorithm is useful for every cooling method and needs few inputs. The algorithm analytically predicts convective and radiative heat flux from combustion chamber. The results have been compared with the experimental data as well as the numerical results for different geometries, O/F ratios, propellants, and combustion chamber pressures. According to the results, presented algorithm can suitably predict the heat fluxes with error lower than15 percentage. The algorithm is not involved in implicit solution or numerical complexity and can be used in multidisciplinary design optimization methods that demands rapid heat transfer modeling.
Keywords: Heat Transfer, Heat Flux, Bipropellant, Multidisciplinary Design Optimization.
© Copyright 2015 Authors - This is an Open Access article published under the Creative Commons Attribution License terms. Unrestricted use, distribution, and reproduction in any medium are permitted, provided the original work is properly cited.
Date Received: 2014-11-02
Date Accepted: 2015-11-20
Date Published: 2015-12-21
Nomenclature
- MDO: Multidisciplinary design optimization
- O/F: Oxidant mass by fuel mass ratio
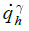 : convective
heat flux
: convective
heat flux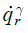 : radiative
heat flux
: radiative
heat flux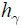 : convective
heat coefficient
: convective
heat coefficient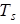 : wall
temperature
: wall
temperature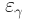 : Radiative
coefficient of hot gas
: Radiative
coefficient of hot gas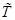 : mean
temperature
: mean
temperature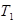 : temperature
before heat transfer
: temperature
before heat transfer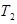 : temperature
after heat transfer (real temperature)
: temperature
after heat transfer (real temperature)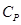 : specific heat
at constant pressure
: specific heat
at constant pressure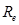 : Reynolds
number
: Reynolds
number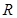 : constant
parameter of gas combustion products
: constant
parameter of gas combustion products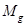 : molecular
weight
: molecular
weight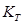 : temperature
correction factor
: temperature
correction factor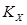 : boundary
layer correction factor
: boundary
layer correction factor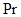 : Prandtl
number
: Prandtl
number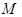 : Mach number
: Mach number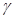 : isentropic
exponent
: isentropic
exponent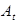 ,
, 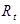 : Throat area,
radius of throat
: Throat area,
radius of throat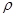 : Density of
gas
: Density of
gas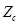 : correction
factor for area
: correction
factor for area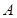
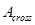 : cross-area
: cross-area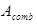 : combustion
chamber cross section
: combustion
chamber cross section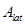 : total
lateral surface including nozzle surface
: total
lateral surface including nozzle surface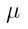 : Viscosity
coefficient
: Viscosity
coefficient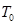 : combustion
temperature (T-core)
: combustion
temperature (T-core)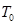 : combustion
temperature (T-core)
: combustion
temperature (T-core)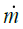 : Mass flow
: Mass flow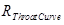 : Curvature
radius of the throat
: Curvature
radius of the throat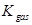 : conductivity
of combusted gases
: conductivity
of combusted gases
1. Introduction
Liquid thrusters are widely used in space applications especially for orbital maneuvers and launch vehicles. New missions demand new propulsions with lower cost. Additionally, new materials and propellants will improve the propulsion performances so, new bipropellant propulsions will be born. Modern designing methods such as multidisciplinary design optimization (MDO) are used to derive an optimum solution. Optimization of complex engineering systems has always been an integral part of the design. Due to the size and complexity of the systems, the design of a whole system is broken down into multiple disciplines. All disciplines should be simultaneously optimized to find a global optimum. Time consumption is a disadvantage and always tries to reduce the elapsed time. In preliminary design phase, semi-accurate model of each discipline is usually used to analyze many configurations in a shorter elapsed time. One of the most important disciplines in multidisciplinary design optimization of the bipropellant propulsion is thermal-control and cooling.
The purpose of a thermal-control is to maintain all thrusters’ components within the allowable temperature. It is only obtained by control of heat fluxes from a combustion chamber. Because of high combustion temperatures (up to 3700K) and high heat flux rates (peak may go beyond 160 MW/m2) from the hot gases to the chamber wall, thruster cooling is a major design consideration. Two approaches are available to encounter [1], [2]. The first one is steady state method, which the heat transfer rate through combustion wall and temperature on the wall are constant, in other words, there is a thermal equilibrium. The second method is transient heat transfer method. For this method, there is no thermal equilibrium and the temperature on combustion wall continuously increases. The propulsion system has to be stopped before the temperature reaches the critical point. For continues thrust regime in space mission, steady state methods should be provided. Regenerative, transpiration, radiative, ablative and film cooling are generally used to control heat fluxes of combustion chamber and to provide suitable structure temperatures [3], [4].
Regenerative cooling is the most widely used method of cooling a high performance combustion chamber. It is accomplished by flowing high velocity coolant over the backside of the chamber hot gas wall to convectively cool the wall [5], [6]. The coolant, heated up by the hot liner, is then discharged into the injector and used as a propellant. Engines that have this kind of cooling are, for example, the AETUS II, RL10A, RD861Kand VINCI [7]. Ablative cooling uses a particular combustion gas-side wall material that is sacrificed, by melting, vaporization and chemical changes to dissipate heat. As a result, relatively cool gases flow over the wall surface, thus lowering the boundary-layer temperature and assisting the cooling process. Radiative cooling radiates the heat away from the surface of the outer chamber walls. An example of entirely radiation-cooled thruster is the RS-21 Mariner/Viking Orbiter spacecraft. Transpiration cooling is accomplished by introducing a coolant (gaseous or liquid) through porous chamber walls at a rate sufficient to maintain the desired combustion chamber wall temperature. This technique was applied to cool the injector faces of the J-2, RS-44 and SSME. Film cooling protects the chamber walls from excessive heat with a thin film of coolant. Coolant is injected through orifices near the injector or near the throat with special slots. This method has been widely used, in particular, for high heat fluxes [8]-[10].Sample engines were film cooling is applied are the SSME, Vulcain2, RD-171and RD-180.Combinations of mentioned methods are nowadays used [11] to increase the thermal performances. Combination of regenerative and film cooling is more interesting because of good performance without activity limitation.
Good thermal control needs good heat fluxes approximation. Nowadays, many numerical methods and commercial tools have been developed which try to improve modeling of heat fluxes. All of the methods and tools need many parameters and times to run. Such inputs may be available for existing thrusters but some required inputs are not accessible in preliminary design phases. Rapid heat transfer modeling is especially required for preliminary design phases. Although such an algorithm has lower accuracy but faster heat transfer modeling make a good possibility to analyze many configurations for deriving best performance. In this paper, engineering model for heat transfer will be introduced which can be applied in MDO algorithms.
2. Heat Transfer Modelling
Thermal-control of bipropellant thrusters is one of the most important disciplines in propulsion design algorithm. Hard coupling between thermal limitation and thruster’s performance (such as pressure, mass flow, O/F ratio…) takes place because one of the propellant (usually fuel) is simultaneously involved in different disciplines [4], [12]. The largest part of the heat transfer from the hot chamber gases to the chamber walls is by convection and radiation. The amount of heat transfer by conduction is small and usually negligible in preliminary design phases.
Combustion products lose energy by convection ![]() and radiation
and radiation ![]() . Finally heat fluxes are
emitted by radiation or be absorbed by some other coolant from lateral surface.
. Finally heat fluxes are
emitted by radiation or be absorbed by some other coolant from lateral surface.
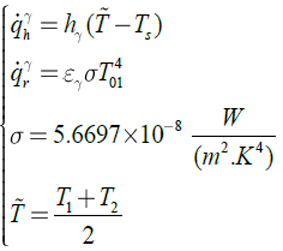
![]() is wall temperature,
is wall temperature, ![]() is mean temperature and
is mean temperature and ![]() is a temperature after heat transfer (real
temperature).
is a temperature after heat transfer (real
temperature). ![]() is calculated
by solving the energy equilibrium . Prediction of convective heat coefficient (
is calculated
by solving the energy equilibrium . Prediction of convective heat coefficient (![]() ) is most important part
of thermal modeling of every combustion chamber. A few analytical models are
available to predict
) is most important part
of thermal modeling of every combustion chamber. A few analytical models are
available to predict ![]() . Bartz at 1963
[13] proposed empirical correlations (2) for prediction of
. Bartz at 1963
[13] proposed empirical correlations (2) for prediction of ![]() which is widely
used. There was no offer for
which is widely
used. There was no offer for ![]() .
.
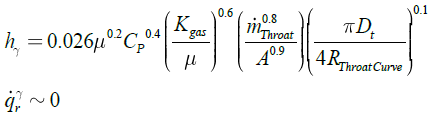
Pavli and et al. at 1966 [14] presented relation
(3) which was included the Reynolds number ![]() and two correction factors to improve the behavior
of the original Bartz equation. A temperature correction factor
and two correction factors to improve the behavior
of the original Bartz equation. A temperature correction factor ![]() had been added, taking
into account that the new reference temperature is calculated halfway between
the wall and the free stream static temperature. Moreover, since the geometric
reference parameter in the original Bartz equation was the throat diameter, a
further correction factor
had been added, taking
into account that the new reference temperature is calculated halfway between
the wall and the free stream static temperature. Moreover, since the geometric
reference parameter in the original Bartz equation was the throat diameter, a
further correction factor ![]() had been added
for the consideration of the boundary layer growth in the cylindrical part and
at nozzle.
had been added
for the consideration of the boundary layer growth in the cylindrical part and
at nozzle.
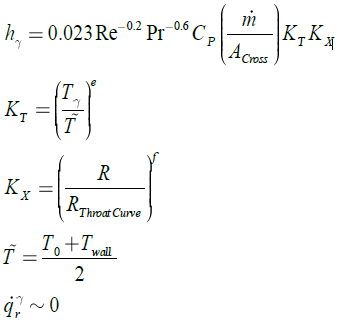
Huzel and et al. at 1992 [1] proposed equations
(4) for prediction of ![]() and
and ![]() . More quality of flow
including Mach number and pressure were taken into account.
. More quality of flow
including Mach number and pressure were taken into account.
At 2001, ref [15] presented relation (5) based on two mentioned correction factors and the effect of cross section was augmented.
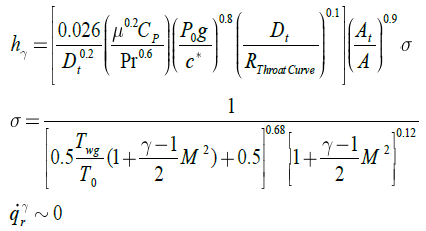
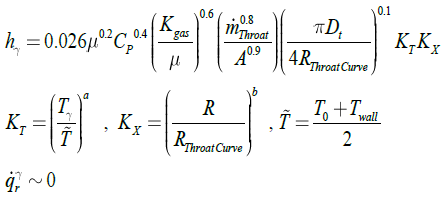
Finally Sutton at reference [16]
proposed equations (3) for prediction of ![]() and
and ![]() .
.
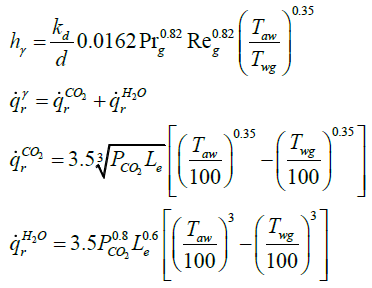
All mentioned equations need wall temperature to
calculate heat fluxes. In fact, correction factor usually have been developed
based on temperature ratio. For rapid thermal modeling of combustion chamber,
wall temperature should be a solution of energy equations and if ![]() be involved in wall
temperature then implicit solution is derived instead of direct solution.
Furthermore, above equations, need many inputs (
be involved in wall
temperature then implicit solution is derived instead of direct solution.
Furthermore, above equations, need many inputs (![]() ) that are not usually available in preliminary
design phase.
) that are not usually available in preliminary
design phase.
3. Rapid Heat Transfer Modeling
According to the mentioned relations, ![]() is a function of
following terms.
is a function of
following terms.
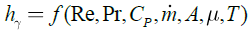
Compression between equation (7) and convective heat coefficient of flat plat offers equation (8):
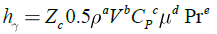
Using mass flow equilibrium through the combustion and nozzle leads to equation (9).
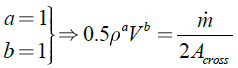
![]() is cross-area of every section and
is cross-area of every section and ![]() is related mass flow. Other exponents and correction factors are suggested as below.
is related mass flow. Other exponents and correction factors are suggested as below.
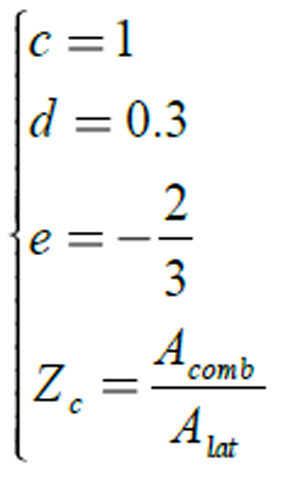
Where, ![]() is combustion chamber cross section and
is combustion chamber cross section and ![]() is total lateral surface
including nozzle surface. New correction factor presents the effect of geometry
(length and diameter) and 2-D heat transfer in structure. Replacing equations
(9) and (10) in equation (8) finally leads to equation (11).
is total lateral surface
including nozzle surface. New correction factor presents the effect of geometry
(length and diameter) and 2-D heat transfer in structure. Replacing equations
(9) and (10) in equation (8) finally leads to equation (11).
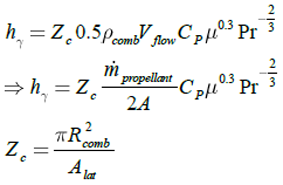
![]() is the Prandtl number,
is the Prandtl number, ![]() is viscosity,
is viscosity, ![]() is specific heat at constant volume and
is specific heat at constant volume and ![]() is cross section of flow(
is cross section of flow(![]() ) and
) and ![]() is correction factor
depended on combustion chamber geometry. Equation (12) presents supplementary
relations [16], [4] when exact parameters of flow are not available.
is correction factor
depended on combustion chamber geometry. Equation (12) presents supplementary
relations [16], [4] when exact parameters of flow are not available.
![]() is a constant parameter of gas combustion
products,
is a constant parameter of gas combustion
products, ![]() is an isentropic
exponent,
is an isentropic
exponent, ![]() is molecular
weight and
is molecular
weight and ![]() is combustion
temperature (T-core).
is combustion
temperature (T-core). ![]() ,
, ![]() and
and ![]() can be derived from [17] for every propellant. Finally, heat transfer modeling can summarily be presented as figure (1).
can be derived from [17] for every propellant. Finally, heat transfer modeling can summarily be presented as figure (1).
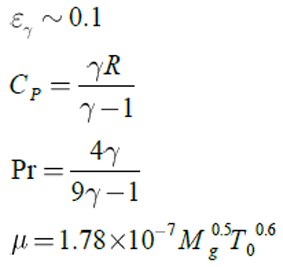

4. Validation
Validation of heat transfer usually concentrated
in prediction of ![]() and
and ![]() . Validation has been done
by numerical results and experimental data [18], [15]. The results of the
presented algorithm and the results of numerical methods have been compared at
table 1 and table 2 for following two cases.
. Validation has been done
by numerical results and experimental data [18], [15]. The results of the
presented algorithm and the results of numerical methods have been compared at
table 1 and table 2 for following two cases.
| Case-1 | Case-2 |
 |
 |
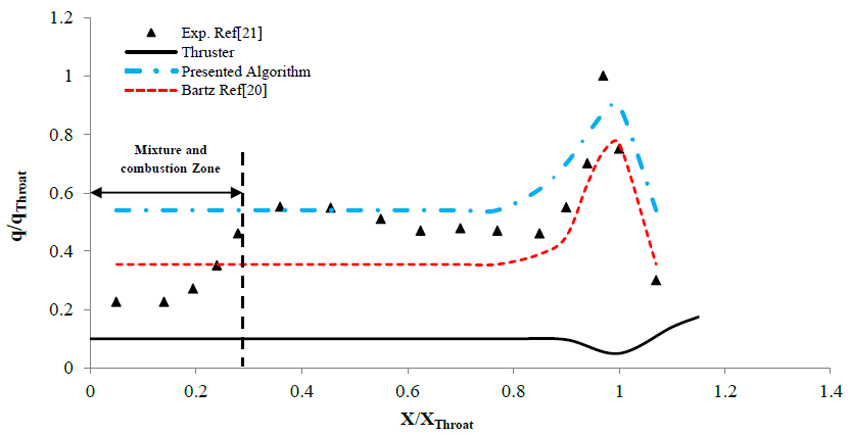
According to the results, presented model can suitably (Error < 15percentage) predict heat transfer. Experimental results have been presented as dimensionless for following conditions:
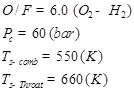
Figure (2) shows the comparison between the results of presented algorithm (14 sections) and experimental data.
Table 1. Results comparison for the case-1.
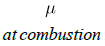 |
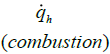 |
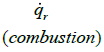 |
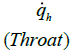 |
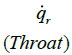 |
|
| Bartz relation | 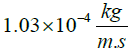 |
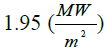 |
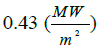 |
 |
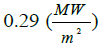 |
| Presented Algorithm | 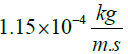 |
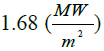 |
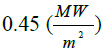 |
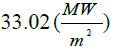 |
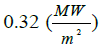 |
| Error | 10% | 14% | 5% | 15% | 10% |
Table 2. Results comparison for the case-2.
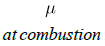 |
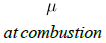 |
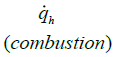 |
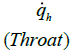 |
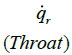 |
|
| Bartz relation | 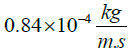 |
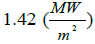 |
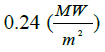 |
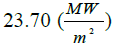 |
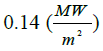 |
| Presented Algorithm | 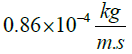 |
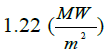 |
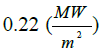 |
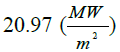 |
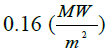 |
| Error | 3% | 14% | 9% | 11% | 15% |
According to the results, algorithm can suitably
predict heat fluxes after complete combustion (better than Bartz). It should be
noted that the presented algorithm do not need wall temperature to calculate ![]() and wall temperature is
only needed to calculate the heat fluxes. Calculated heat fluxes by presented
algorithm can be used for every cooling method. It is clear that real
combustion chamber temperature should be sequentially updated (instead of
adiabatic temperature) if energy losing occurs (radiation, ablation …).
and wall temperature is
only needed to calculate the heat fluxes. Calculated heat fluxes by presented
algorithm can be used for every cooling method. It is clear that real
combustion chamber temperature should be sequentially updated (instead of
adiabatic temperature) if energy losing occurs (radiation, ablation …).
5. Summary and Results
In this paper, heat fluxes modeling of combustion chamber has been introduced. Previous relations such as Bartz and Pavli have been reviewed that need some parameters, which are not available for new thrusters in preliminary design phase. New relations for convective and radiative heat fluxes have been presented which can be applied in MDO. Presented algorithm derives the convective heat coefficient as a function of mass flow, O/F ratio, pressure, and cross sections. General advantages of the presented algorithm are summarized as applicability for any propellant and thrust value, analytical solution and demanding a few inputs. Results have been compared with numerical methods as well as experimental data for different propellant, O/F ratio, combustion pressure, and wall temperature. According to the results, algorithm can suitably predict heat fluxes after complete combustion. Therefore, algorithm can be applied in preliminary design phase.
References
[1] D. K. Huzel and D. H. Huang, Modern Engineering for Design of Liquid-Propellant Rocket Engines, Washington: American Institute of Aeronautics and Astronautics, 1992. View Book
[2] M. Bai, “Numerical Evaluation of Heat Transfer and Pressure Drop in Open Cell Foams,” MSc thesis, Florida: University of Florida, 2007. View Article
[3] M. Trotti, “Modelling of liquid film cooling in a GOX/Kerosene rocket combustion chamber,” Ph.D. dissertation, Italy: Politecnico Di Milano, 2011-2012. View Article
[4] A. Amirhossein, “Multidicsiplinary Design Optimization of Reentry Vehicle considering Guidance Algorithm,” Ph.D. dissertation, Iran: Amirkabir University of Technology, 2015.
[5] Y. Torres, L. Stefanini and D. Suslov, "Influence of Curvature in RegenerativeCooling System of Rocket Engine," Progress in Propulsion Physics, vol. 1, pp. 171-184, 2009. View Article
[6] M. Pizzarelli, F. Nasuti and M. Onofri, "Trade-off analysis of high-aspect-ratio-cooling-channels for rocket engines," International Journal of Heat and Fluid Flow, vol. 44, pp. 458-467, 2013. View Article
[7] M. E. Boysan, “Analysis of regenerative cooling in liquid preopellant rocket engines,” MSc thesis, Turkey: Middle East Technical University, 2008. View Article
[8] R. Arnold, D. I. Suslov and O. J. Haidn, "Film cooling of accelerated flow in a subscale combustion chamber," Journal of propulsion and power, vol. 25, no. 2, pp. 443-451, 2009. View Article
[9] R. Arnold, D. I. Suslov and O. J. Haidn, "Film cooling in a high-pressure subscale combustion chamber," Journal of propulsion and power, vol. 26, no. 3, pp. 428-438, 2010. View Article
[10] Babaee and Hessam, “Analysis and Optimization of Film Cooling Effectiveness,” Ph.D. dissertation, Louisiana: Louisiana State University, 2013. View Article
[11] O. Knab, M. Frey, J. Görgen, C. Maeding, K. Quering and D. Wiedmann, "Progress in Combustion and Heat Transfer Modelling in Rocket Thrust Chamber Applied Engineering," in 45th AIAA/ASME/SAE/ASEE Joint Propulsion Conference & Exhibit, Colorado, 2009. View Article
[12] H. Darabi, J. Roshanian and H. Zare, "Design of liquid-propellant engine using collaborative optimization and evolutionary algorithms," in Proceedings of the Institution of Mechanical Engineers, Part G: Journal of Aerospace Engineering, Spain, 2014. View Article
[13] D. R. Bartz, "Turbulent boundary-layer heat transfer from rapidly accelerating Wow of rocket combustion gases and of heated air," Jet Propulsion Laboratory, California, Tech. Rep. NASA-CR-62615, 1963. View Article
[14] A. J. Pavli, J. K. Curley, P. A. Masters and R. M. Schwartz, "Design and Cooling Performance of a Dump Cooled Rocket Engine," NASA, Washington, Tech. Memo. D-3532, 1966. View Article
[15] T. D. Astrium, "Final report on data correlation and evaluation of test results phase 1 part 1," Astrium, Contract GSTP-2-TN-06-Astrium, Final Rep., 2001.
[16] G. P. Sutton and O. Biblarz, Rocket Propulsion Elements, New Jersey: John Willy & Sons Inc., 2010. View Book
[17] S. Gordon and B. J. McBride, Computer program for calculation of complex chemical equilibrium compositions and applications, Ohio: NASA, Tech. Rep., 1994. View Article
[18] F. Di Matteo, “Modelling and Simulation of Liquid Rocket Engine Ignition Transients,” Ph.D. dissertation, Rome: Sapienza University of Rome, 2011. View Article

