Volume 2 - Year 2015 - Pages 34-39
DOI: 10.11159/jffhmt.2015.005
Experimental Characterization of a Two-Phase Heatsink
Bruno Agostini, Mathieu Habert
ABB Switzerland Ltd., Corporate Research
Segelhofstrasse 1K, 5405 Daettwil, Switzerland
Bruno.agostini@ch.abb.com; Mathieu.habert@ch.abb.com
Abstract - There is a continuous trend to increase power density in power electronics while traditional cooling methods like heat sinks cannot cope with this increase anymore. Cooling with two-phase thermosyphons allows to cool higher heat density without pump. Standard thermosyphon technology only works in vertical position because it uses gravity to move the phase changing fluid and has a fixed shape that cannot retrofit heatsinks in current product designs. This is a limitation for many products that would need a complete redesign to accommodate for a new air flow configuration. Hence, there is a need for thermosyphons working in vertical and possibly horizontal orientations and that can retrofit heatsinks, with performances allowing increase in power density. This article presents the experimental characterization of a new type of thermosyphon to fulfill these constraints.
Keywords: thermosyphon, heat-sink retrofit, two-phase cooling, power electronics.
© Copyright 2015 Authors - This is an Open Access article published under the Creative Commons Attribution License terms. Unrestricted use, distribution, and reproduction in any medium are permitted, provided the original work is properly cited.
Date Received: 2014-11-10
Date Accepted: 2015-07-09
Date Published: 2015-12-15
1. Introduction
Two-phase thermosyphon is a cooling technology gaining momentum for thermal management of electronics. Nowadays heat pipes are standard cooling devices in laptops and have attracted the interest of the power electronics industry. For example, in his state-of-the art review, Vasiliev [1] described the use of heat pipes for power semiconductors cooling, highlighting that it allows for higher power density. The use of dielectric fluids and pumpless operation altogether with high heat transfer coefficients is an attractive combination for power electronics thermal management. Well before the developement of the pulsating heat pipe by Akachi [2], of the looped heat pipe by Maydanik [3] and of the heat pipe by Grover[4], gravity two-phase loops were used since the steam age in locomotive boilers and working ovens. More recently these technologies were embraced by the computer industry, for example with the development of silent CPU coolers by Pastukhov and Maydanik [5]. When vertical orientation is possible, gravity two-phase loops using small channels are particularly appealing for their compactness and low material and fluid use. However, very few experimental data or models are available with the new dielectric fluids at the required working temperatures and channel diameters. Furthermore, small diameter channels allow taking advantage of the so called bubble pump effect to further increase the performances of the thermosyphon. This effect causes liquid plugs to be propelled in the channels and delay dry-out phenomena. This liquid plug lifting effect typically shows a maximum with heat load as shown by Delano [6] and was further studied by Agostini and Habert [7], Agostini and Ferreira [8] in a transparent capillary sized two-phase loop where mass flow rates of liquid could actually be measured with a double laser beam technique. This bubble pumping effect was the starting point for design a thermosyphon that could retrofit a standard heatsink since in such a configuration the evaporator and condenser would be at the same height so that only the void fraction difference between the boiling and condensation would provide buoyancy effect to move the fluid. The bubble pumping would then provide an additional driving force. A first concept was developed by Agostini [9] using aluminium multiport extruded tubes found in automotive heat exchanger. The new concept presented here aims at higher cooling power and uses plate and bar heat exchanger technology.
Maydanik et al. [10] compared the design and performances of two-phase loop heat pipes and thermosyphons and concluded that they yield simpler design and lower cost but at the same time are quite efficient heat-transfer devices capable of operating in a wide range of variation of parameters.
Franco and Filippeschi [11] tested a closed loop two-phase thermosyphon and studied the influence of several parameters on the performances: heat load, operating pressure and fluid filling. The limits in the heat and mass transport were evidenced together with the unstable behaviour at the high heat input in order to design and build a two-phase thermosyphon for systems like solar heating.
Chehade et al [12] presented an analytical model for a thermosyphon loop developed for cooling air inside a telecommunication cabinet. Depending on the model, it is shown that increasing the liquid and vapor lines section diameters to 0.012 m and 0.014 m could be one of the vital keys to improve the system thermal efficiency. The increase of the external ambient temperature increases the mass flow rate in the loop, decreases the evaporator pressure drop and reduces the cooling performance. The mean deviation between the predictions of the theoretical model with the measurements for operating temperature is about 6%.
2. New Concept of Two-Phase Heatsink
Several views of this new concept of two-phase heatsink are shown in Fig. 1 (exploded CAD view) and Fig. 2 (photography of the actual prototype) in order to illustrate the working principle and the dimensions are shown in Tab. 1. This two-phase heatsink is essentially using a combination of plate and bar heat exchanger technology and aluminium multiport extruded tubes to enable the bubble pumping effect in capillary sized channels. It is composed of the following elements:
- 13 sets of plates in parallel separated by flat top type air fins in the condenser section and by aluminium spacers in the evaporator section,
- >6 MultiPort Extruded (MPE) tubes arranged in parallel between each pair of plates,
- a length of plates with no MPE tube enclosed at the top and bottom form a pair of manifold where the fluid can turn to flow from the evaporator to the condenser and the other way around.
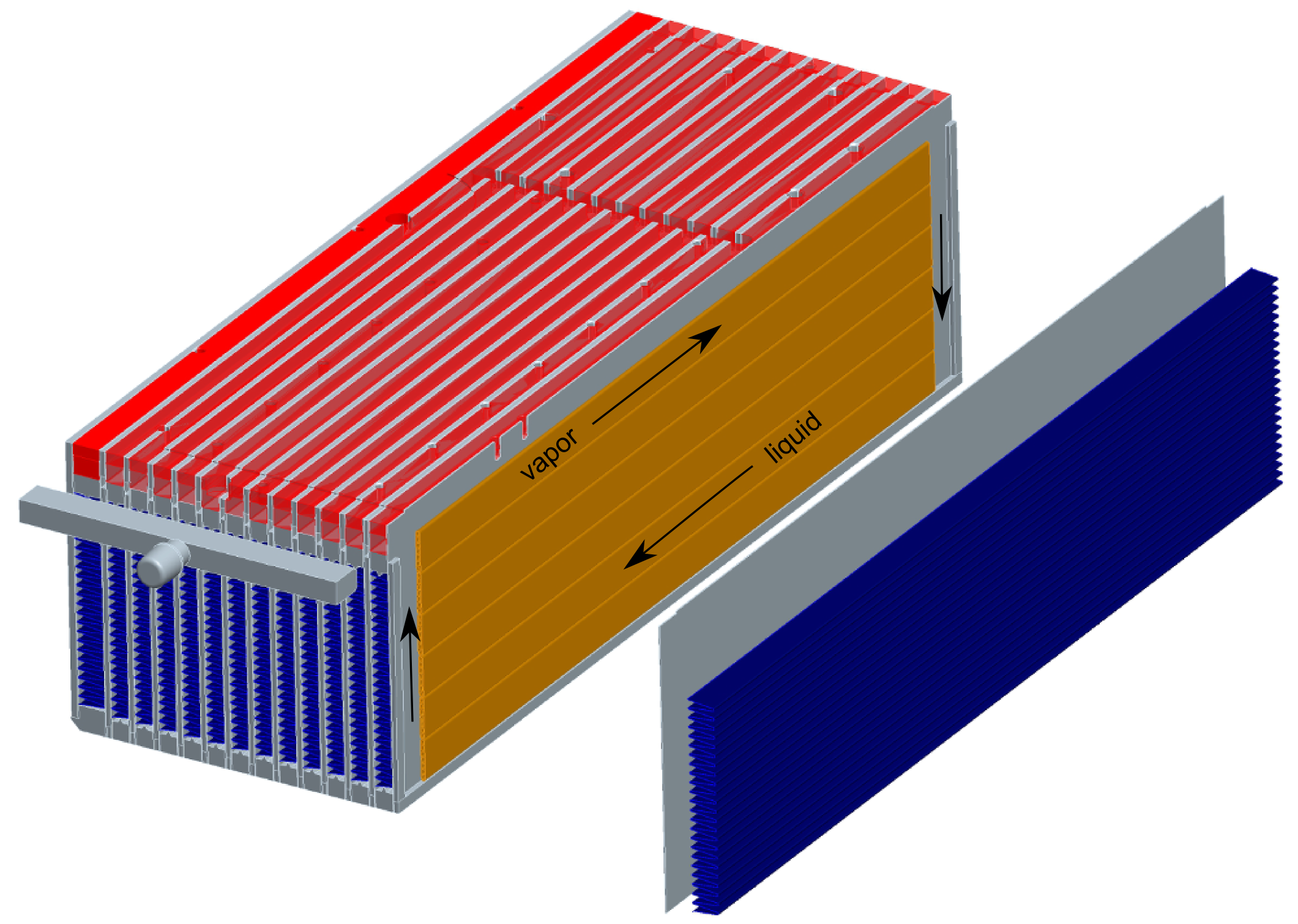

Table 1. Geometry of the two-phase heatsink.
| Core | Condenser | Evaporator |
| Dimensions | 415x163.5x103 | 415x163.5x22 |
| Number of channels | 38 | 4 |
| Air fin height (mm) | 8 | - |
| Air fin pitch (mm) | 4 | - |
| Air fin type | Flat top | - |
| Channel height (mm) | 1.12 | 1.12 |
| Channel fin type | MPE tube 18x2x0.4 | MPE tube 18x2x0.4 |
| Channel fin pitch (mm) | 2.54 | 2.54 |
| Manifold dimensions (mm) | 108x18x2 | 108x18x2 |
Note that the MPE tubes where the boiling occurs have capillary sized channels so that a bubble pumping effect will occur in order to move the liquid slugs towards the inlet of the evaporator and thus prevent dry-out and give a more uniform baseplate temperature. As a consequence, as illustrated in Fig. 1, the fluid will evaporate in the section of channels corresponding to the heating area (red blocks), and will condense in the section of channels corresponding to the cooling area (blue air fins). The direction of circulation of the two-phase fluid will change depending on the orientation.
3. Experimental Setup
A schematics of the test facility is shown Figure 3. This test facility is composed of the following elements: the test section, two power controllers for the electrical supply of the heating modules, an inlet air distribution cone equipped with 1 thermocouple and an air pressure measurement port, an outlet air collection cone equipped with 3 thermocouples and an air pressure measurement port and a differential air pressure sensor. The test section equipped with the following instrumentation: a first power module at the bottom of the evaporator (IGBT), a second power module at the top of the evaporator (diode), 1 absolute pressure sensor connected to the filling valve with a T junction, surface mounted and thermally insulated from ambient thermocouples at three location along the back of the condenser to measure the internal fluid temperature (bottom, middle and top) and 8 thermocouples inserted in grooves machined in the baseplate at the location of the power modules hotspots.
All signals are acquired through a National Instruments SCXI box equipped with a 1102 module with a cut off frequency at 2 Hz and connected to a laptop running Labiew. The measuring devices and their accuracy are presented in Tab. 4. The test setup is inserted into a wind tunnel equipped with a centrifugal fan, a mass flowmeter, a pre-heater, and an air-water heat exchanger connected to a chiller in order to keep the air at a preset temperature. All the thermocouples were calibrated using an Omega DP97 precision thermometer with platinum probes to measure the reference temperature and a Lauda R207 chiller to control the temperature. The uncertainty of the calibrated thermocouples is ± 0.1 K (it is ± 1.5 to 2.5 K if not calibrated). The three air temperature sensors at the exit of the condenser are evenly distributed over the width of the air stream in order to capture as much as possible potential air flow non uniformities. Based on the classical error propagation method and the individual instruments accuracies the total uncertainty on the thermal resistance was estimated to vary from 20% at low heat load to 5% at high heat load.
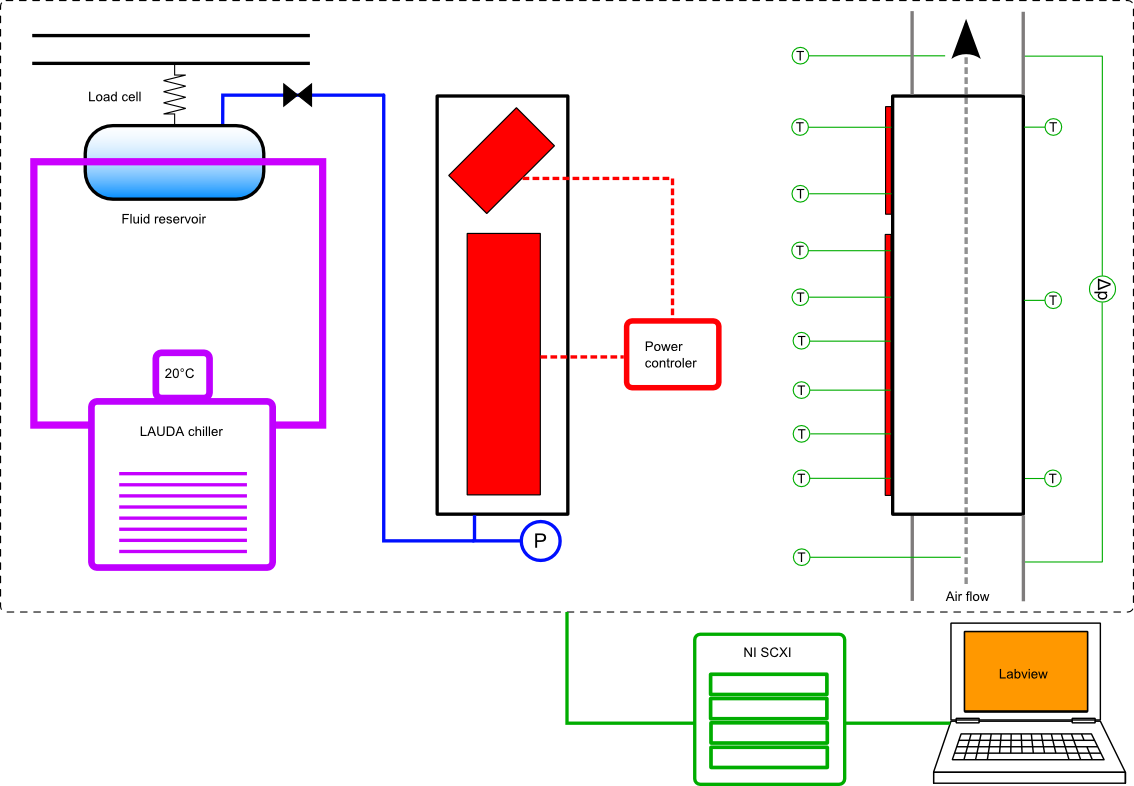
Table 2. Measuring devices and accuracy.
| Measurement | Device | Measured range | Accuracy | Unit |
| Power | Xantrex power supply | 0-12000 | ± 96 | (W) |
| Power | Eurotherm controler TE40A | 0-3800 | ± 77 | (W) |
| Air temperature | TC type K 1.5 mm | 15-60 | ± 0.1 | (° C) |
| Base temperature | TC type K 0.5 mm | 25-110 | ± 0.1 | (° C) |
| Fluid temperature | TC type K 1 mm | 25-110 | ± 0.1 | (° C) |
| Evaporator pressure | ABB 261AS | 0-3000 | ± 4.5 | (kPa) |
| Condenser pressure | Omega PX409 | 0-1724 | ± 1.4 | (kPa) |
| Air pressure drop | Huba Control 698.900100201 | 0-100 | ±2 | (Pa) |
| Air flow rate | ABB Topaz | 80-4000 | ±4 | (kg/h) |
| Fluid weight change | Omega S-Beam load cell LCR-25 | 0-12500 | ±1 | (g) |
4. Measurements
This prototype was tested with refrigerant R1245fa as a working fluid because its saturation pressure is well below the bursting pressure of the cooler and it has the required safety properties to be used in electrical products. Figure 4 shows the variation of the temperature rise along the evaporator at 3136 W heat load for various fillings, in vertical (top) and horizontal (bottom) orientation. The first six temperatures correspond to the measurements under the first heating element (IGBT), and the last two of those under the second heating element (diode). In vertical orientation, increasing the fluid filling increases the temperature rise at the beginning (increased subcooling) of the evaporator and decreases it at the end (decreased dry-out). The hotspot temperature is situated at the end of the evaporator at low filling and in the middle at high filling, showing that dry-out occurs at the end of the evaporator at low filling and that bubble pumping is not sufficient anymore to wet the top of the channels. The optimal filling is passed once the hotspot is situated in the middle of the evaporator and starts increasing with the filling (>66%). In this case, increasing the filling is not useful for suppressing dry-out but will simply increase the working pressure and hence the temperatures in general (91% curve). Note that if more power is applied at the diode location (i.e. closer to the end of the evaporator) then the dry-out effect is greater so that a greater filling is needed for the hotspot location to switch to the middle of the evaporator. In horizontal orientation, the behavior is quite different than in vertical orientation. From 45% to 61% filling the temperature profile remains essentially constant, with only the endmost temperature of the evaporator decreasing by a few Kelvin. Then when the filling reaches 66% the temperature profile shows a tremendous change, with the first temperature increasing by 20 K and the last temperature decreasing by 15 K. This could be the manifestation of a flow reversal since the temperature profile becomes somehow an anti-symmetrical image of that at lower filling and in horizontal orientation gravity does not put any constraint on the flow direction.
Fig. 5 shows the hotspot thermal resistance of the heatsink baseplate in vertical (top) and horizontal (bottom) orientation as a function of the fluid filling for different heat loads. In vertical orientation, the thermal resistance shows a minimum with filling for all heat loads, around 65% at low heat load and around 80% at high heat loads. In horizontal orientation, the thermal resistance shows a minimum with filling around 60% for all heat loads. At the optimal filling the hotspot thermal resistance decreases sharply with heat load increasing from 1.8 kW to 2.5 kW but remains essentially constant above 2.5 kW (not sensitive to fluid filling at high heat load). The thermal resistance versus filling always shows a minimum. The existence of this minimum is due to two competing effects. At low filling ratio the vapour quality at the exit of the evaporator is high, there is not enough liquid to wet the evaporator wall constantly so that the boiling thermal resistance increases. But at high filling ratio there is too much liquid in the thermosyphon so that the condenser is partially flooded. As a consequence the saturation temperature inside the thermosyphon has to increase in order to allow the condenser to condense all the vapour over a shorter flow length.
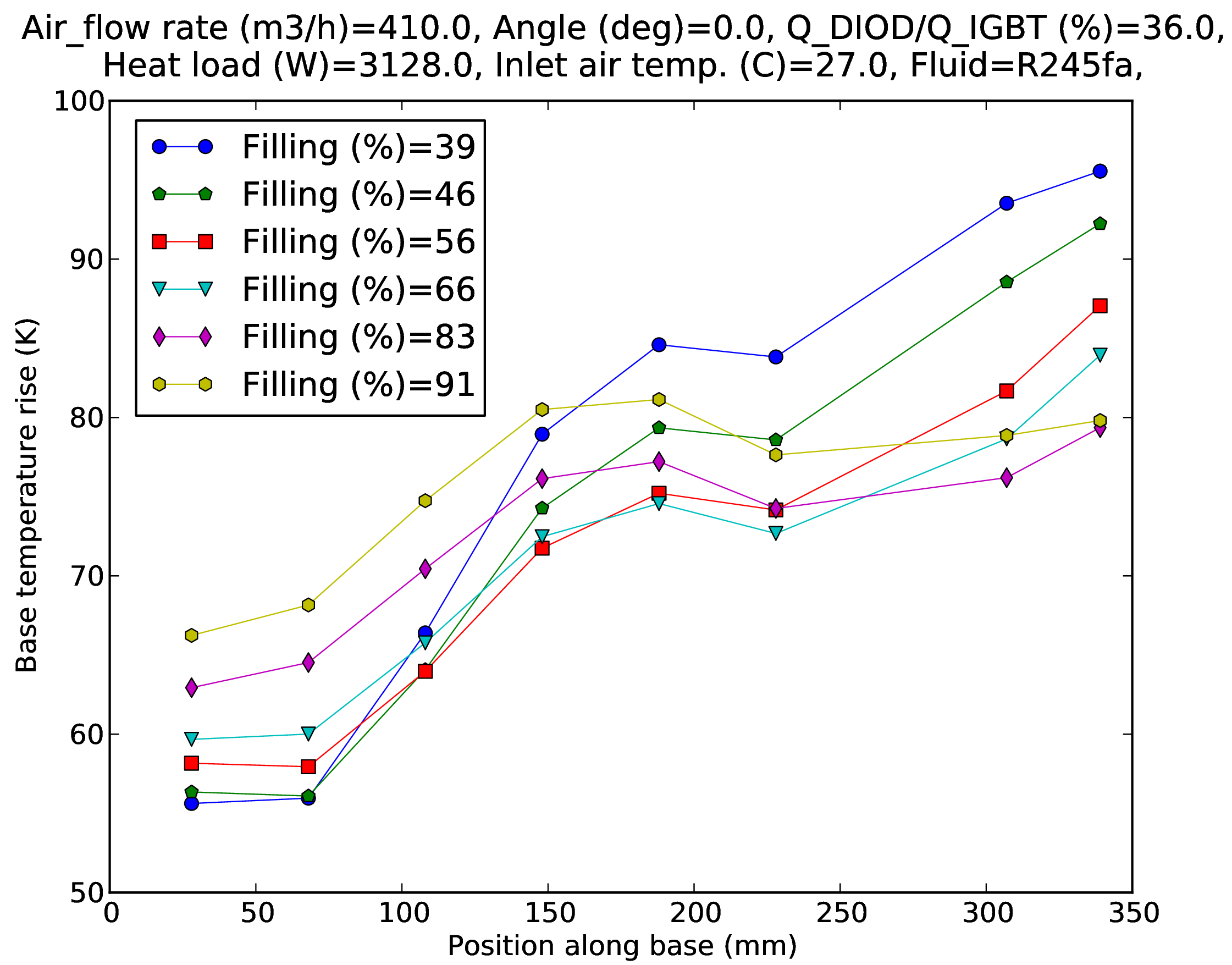
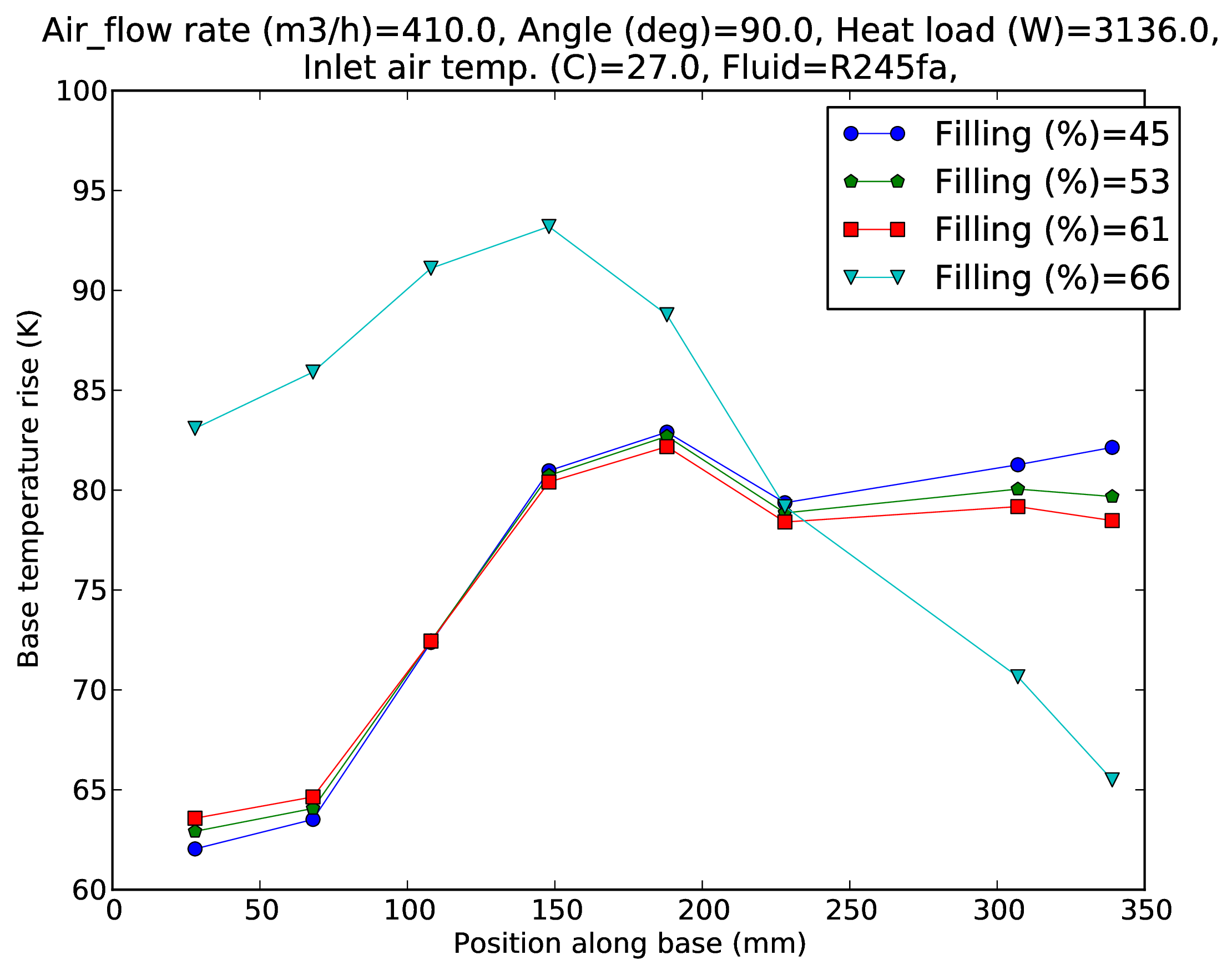
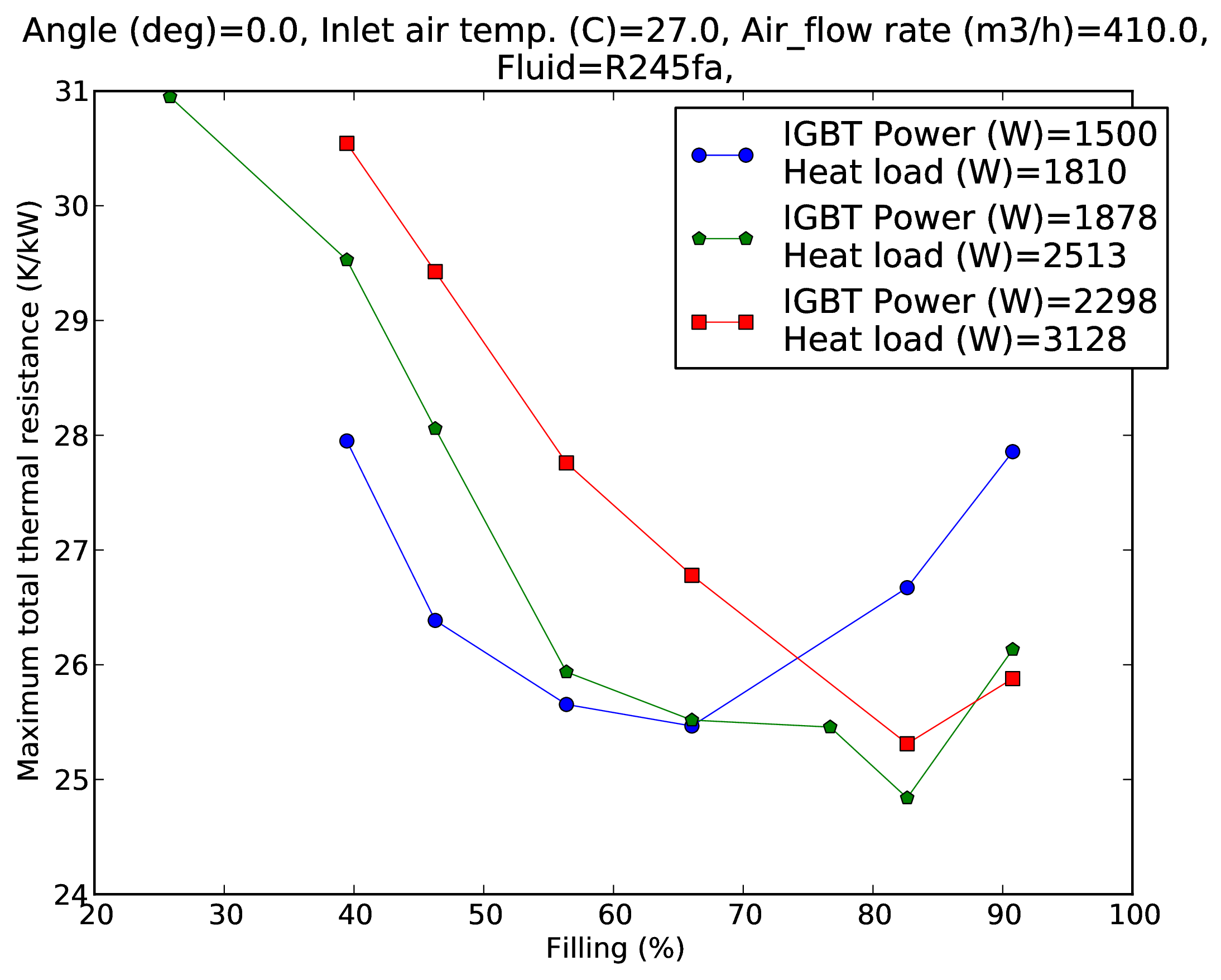
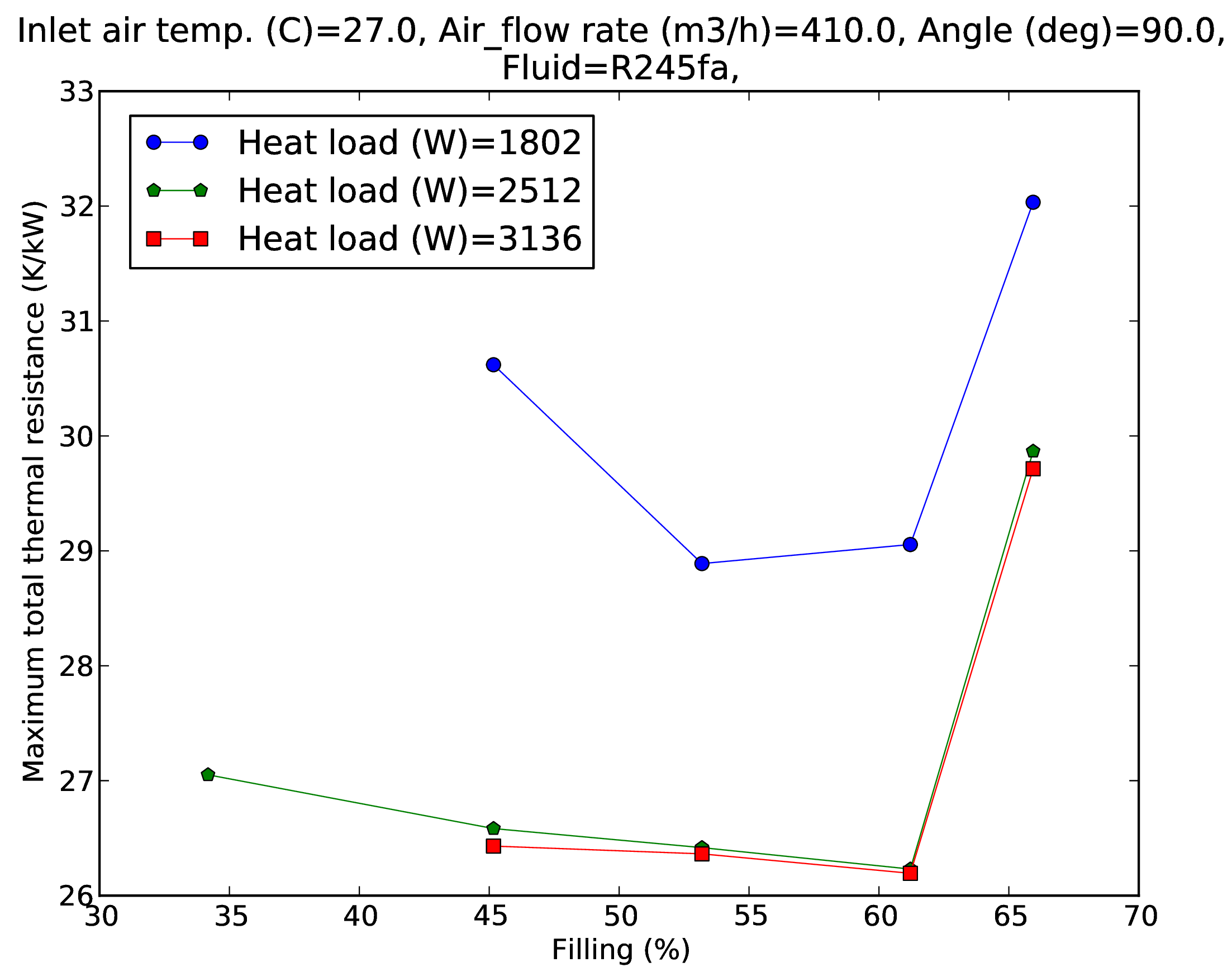
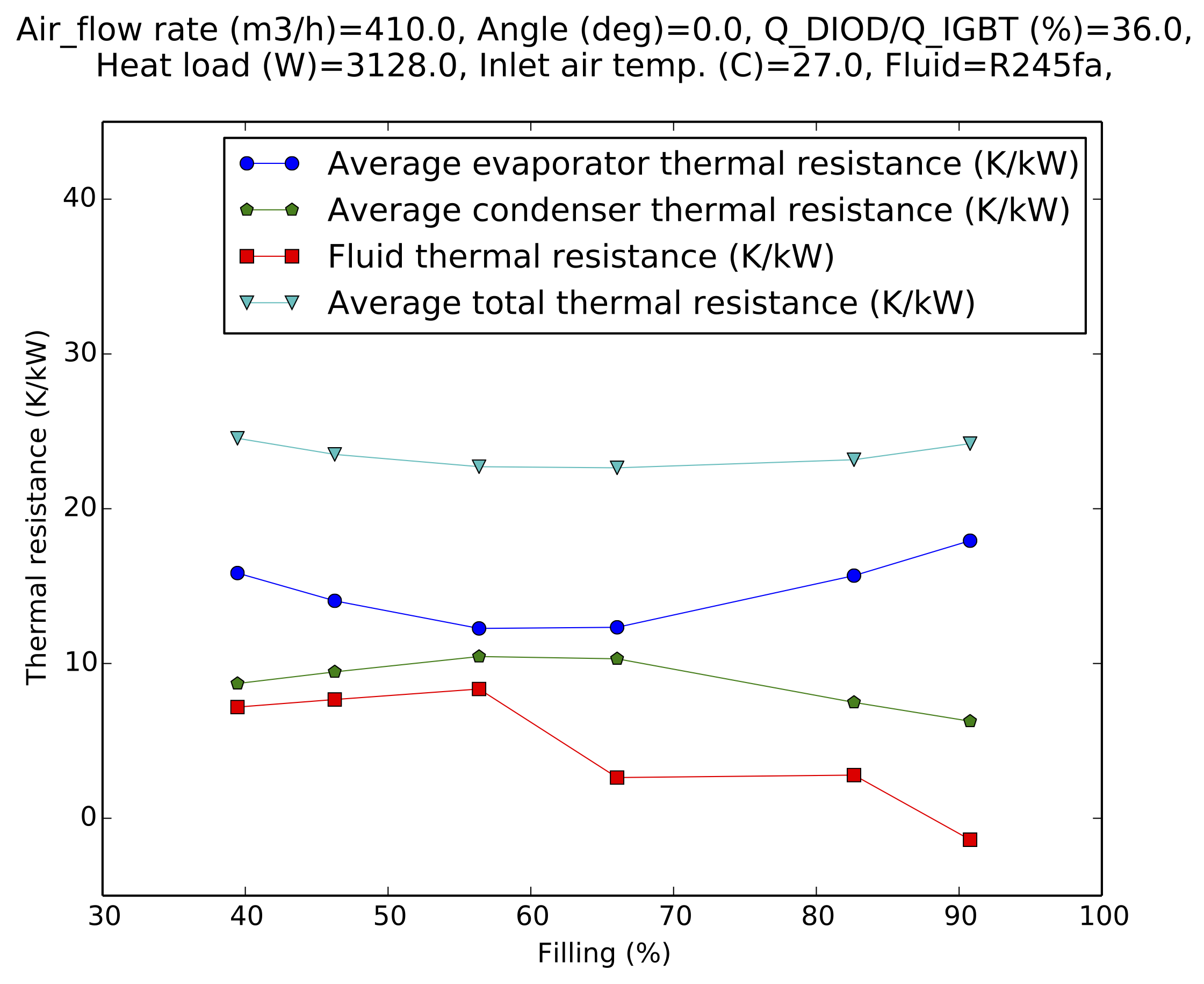
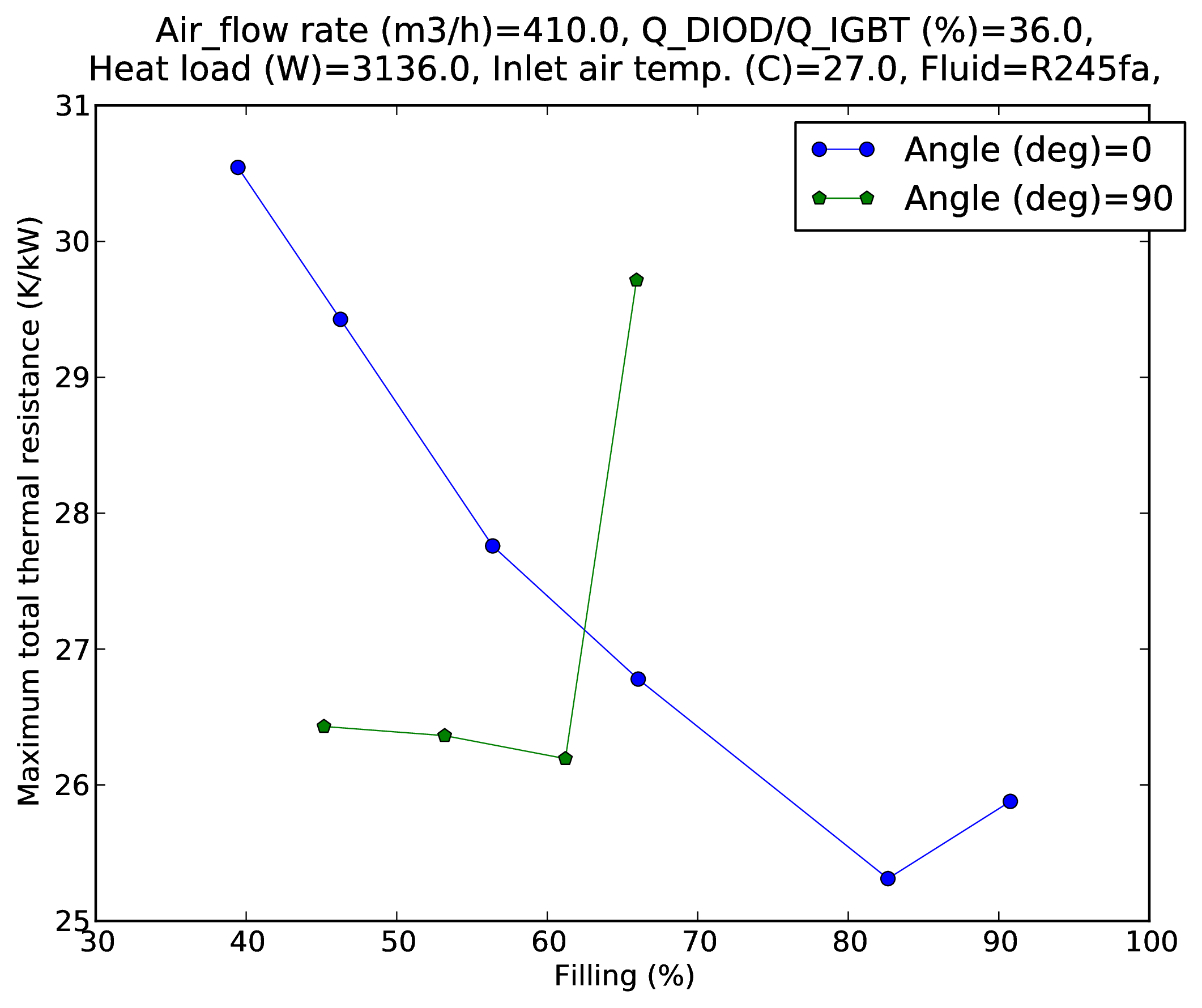
Fig. 6 (top) shows a breakdown of the various thermal resistances in the two-phase heatsink in vertical orientation. The average thermal resistance was used in this plot because it not possible to define a hotspot thermal resistance for the condenser and the fluid. Interestingly the evaporator and condenser thermal resistances are closest and almost equal to each other at the optimal filling ratio. The fluid 'thermal resistance' (temperature difference between the fluid at the condenser inlet and outlet) accounts for about 5 K/kW at the optimal fluid filling (60%), i.e. 16 K at 3140 W losses, which is not negligible and would not occur if the condenser were placed above the evaporator. Without this fluid thermal resistance the temperature rise of the two-phase heatsink could then be 16 K lower. Unfortunately no solution was found to prevent this effect since it is a direct consequence of having the condenser at the same height as the evaporator. Figure 6 (bottom) shows the hotspot thermal resistance versus filling in vertical and horizontal orientation, at 3136 W heat load. There is a modest difference (1 K/kW) when the thermal resistances are compared at the optimal filling, but it appears clearly that the optimal filling is 20 points lower in horizontal orientation. This makes sense since in horizontal position (evaporator facing downwards), the evaporator is much more easily filled with liquid than in vertical orientation.
5. Conclusions
A new type of thermosyphon based on the bubble pumping effect in capillary sized channels was developed with the aim of retrofitting standard heatsinks with a higher performance cooler in existing products such as motor drives for example. Using a combination of plate and bar heat exchanger technology and aluminium multiport extruded tubes a prototype was built and tested. With R1245fa as working fluid, the performances in vertical and horizontal orientation were found to be very close, which is a clear indication that the fluid circulation is driven by the bubble pumping effect rather than by gravity. However when compared to a standard aluminium heatsink at constant fan power, the performance increase was found to be modest, around 5% only. The reason for this lower than expected performances probably comes from the high level of condenser flooding that arises from the necessity of having liquid at least up to the middle of the evaporator in order to avoid dry-out and thus undesirable hotspots at its top. However this results in a high degree of subcooling and therefore a non uniform base temperature along the flow direction.
References
[1] L. L. Vasiliev, "State-of-the-art on heat pipe technology in the former Soviet Union," Applied Thermal Engineering, vol. 18, no. 7, pp. 507-551, 1998. View Article
[2] H. Akachi, "Structure of a heat pipe". USA Patent 4921041 A, 1 May 1990. View Article
[3] Y. F. Maydanik, "Loop heat pipes," Applied Thermal Engineering, vol. 25, no. 5-6, pp. 635-657, 2005. View Article
[4] G. M. Grover, "Evaporation-condensation heat transfer device". USA Patent 3229759 A, 18 January 1963. View Article
[5] V. G. Pastukhov and Y. F. Maydanik, "Low-noise cooling system for PC on the base of loop heat pipes," Applied Thermal Engineering, vol. 27, no. 5-6, pp. 894-901, 2007. View Article
[6] N. Delano, Design analysis of the Einstein refrigeration cycle, PhD thesis: Georgia Institute of Technology, 1998. View Article
[7] B. Agostini and M. Habert, "Measurement, observation and modeling of the performances of a transparent gravity driven two-phase loop," in Advanced Computational Methods and Experiments in Heat Transfer XI, UK, WIT Press, 2010, pp. 227-240. View Article
[8] B. Agostini and E. Ferreira, "Non-intrusive measurement of the mass flow rate inside a closed loop two-phase thermosyphon," Heat Pipe Science and Technology, vol. 2, no. 1-4, pp. 1-12, 2011. View Article
[9] F. Agostini, "Angled thermosyphon loop with horizontal evaporator for power electronics cooling," in Proceedings of ASME Heat Transfer Conference HT2013, Minneapolis, USA, 2013.
[10] Y. F. Maydanik, "Two-phase loop thermosyphons," in Proceedings of VIII Minsk International Seminar "Heat pipes, Heat Pumps, Refrigerators, Power Sources", Minks, Belarus, 2011. View Article
[11] A. F. S. Franco, "Experimental analysis of Closed Loop Two Phase Thermosyphon (CLTPT) for energy systems," Experimental Thermal and Fluid Science, vol. 51, pp. 302-311, 2013. View Article
[12] A. L.-G. H. Chehade, S. Le Masson and E. Lépinasse, "Experimental investigations and modeling of a loop thermosyphon for cooling with zero electrical consumption," Applied Thermal Engineering, vol. 87, pp. 559-573, 2015. View Article

