Journal of Fluid Flow, Heat and Mass Transfer (JFFHMT)

ISSN: 2368-6111

1. Introduction

Swirling flows in burners are common because of the stabilization of lean flames with minimum head losses, ultra low emissions and fuel saving, [1-2]. This issue has important environment implications since the fuel slip due to incomplete combustion is a harmful greenhouse gas.

It is commonly known the mixing capacity is a feature of turbulent flows. It has been widely studied the heat transfer enhancement associated to the swirling flows. Guo et al. [3] carried out a theoretical study about the effect of a secondary flow on the laminar convective heat transfer. Saqr and Wahid [4] proposed an empirical correlation for predicting the entropy augmentation as a function of the swirl number.

Bearing in mind the quantification of thr enhanced heat transfer, Gul and Evin [5] showed that an increase of 300% of heat transfer can be achieved by placing a helical tape at the begining of the test section. Nuntadusit et al. [6] studied the effect on Nusselt number of different set ups of multiple swirling jets.

As for design of the swirl generators, Zohir et al. [7-8] evaluated the increase of heat transfer rate when modifying the location and pitch angle of the swirl generator upwind and downwind the test chamber.

2. Physical Model

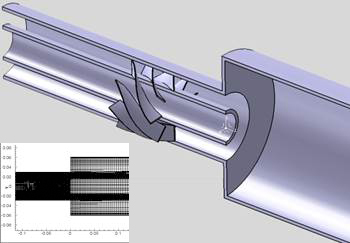
The geometry of the burner is composed by two coaxial nozzles, a swirl generator (a number of fixed vanes on the annular nozzle) and the combustion chamber. Configuration corresponds to the experimental characterization performed by Roback and Johnson [9] being the only difference the swirl injector, such as is depicted in figure 1.

Despite the simple geometrical set-up of the benchmark, the flow pattern shows complex aerodynamic behaviour. The case considers two coaxial jets: one axial and another annular swirling jet. An expansion ratio of 4 in area produces the Outer Recirculation Zone (ORZ) when annular jet enters in the chamber. This kind of configuration has been analyzed by Palm [10] for swirl numbers 0, 0.6 and 1.2.

Main difference in flow pattern between low and large swirling injectors is the presence of an expansion or a recirculation in the centre of the chamber. If swirl number is over 0.6, the flow turns back into the centre and then vortex break down phenomenon appears to form an Inner Recirculation Zone (IRZ), [11]. Both recirculation zones are responsible of high shear and mixture. If swirl number is lower, there is an Inner Divergence Zone instead of the IRZ.

Computational Fluid Dynamics (CFD) has become a useful tool to gain insight of the phenomena involved in thermal and fluid mechanics processes. The simulation requests the generation of a mesh that is a discretization of a continuous geometry into a computational domain. The finite volume Ansys-Fluent was used to carry out the simulations.

The selection of numerical methods is a prerequisite to perform accurate numerical simulations to better predict the performance of the swirling flow burner.

3. Numerical Model

The conservative equations for 3D, steady, turbulent and incompressible flow are solved with a second order scheme looking for better accuracy. Table 1 summarizes the boundary conditions for the nozzle inlets working with air. Passive scalar let identify the mixture fraction associated to the inner jet. As for length scale the hydraulic diameter was considered. Main uncertainty is the transitional flow regime. The 3D mesh has 1.5 million hexahedral cells. The sensibility analysis of mesh resolution revealed that RANS models provide velocity profiles that were independent from meshes for more than 1.5 million cells. Meshes with 0.5, 0.75 1, 1.5 and 2 million cells were tested, as described in [12].

PISO was the algorithm for pressure-velocity coupling since the option provides faster convergence. Multigrid options provide a substantial reduction of the computational time. It consists on solving equations on a coarse mesh to get initial solution to iterate on a finer mesh. However, multigrid is not suitable for reactive cases because the averaging on temperature field is a precursor of the lack of accuracy on the reaction rate. Parallel processing is important to afford resolution of meshes with adequate spatial resolution. The domain decomposition process was established to minimize the processor boundaries and therefore, saving information transfer time.

Table 1. Boundary conditions for nozzles from reference [9].

	Annular inlet	Central inlet
Radio (inner-outer) (m)	0.0128-0.0295	0-0.0125
Velocity (m/s)	1.54	0.66
Temperature (K)	900	300
Turbulent Intensity (%)	7.5	12
Length scale (m)	0.017	0.025
Passive scalar	0	1

4. Turbulence Model

As for the turbulence model, among RANS models of 1, 2 or 4 equations, the most accurate was the k-ε RNG model dominated by the swirl. It is recommended by Ferziger [13-14] to deal with the non-isotropic turbulence associated with the swirling.

The conservation equations for the k and ε are represented in the RNG model as:

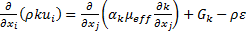
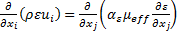
being

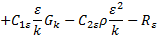
and

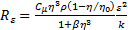
Where k is the turbulent kinetic energy and ε its corresponding dissipation, u denotes the averaged velocities and r the density.

The source term R_ε in equation 2, represents the rate of strain defined in equations (3) and (4). Where S is the strain tensor calculated based on averaged velocities.

The coefficients are summarized in table 2.

Table 2. Constants in the RNG k-ε model.

Cm	C1ε	C2ε	h0	b
0.0845	1.42	1.68	4.38	0.012

Bearing in mind the flow pattern is dominated by recirculation zones and fluid separation of the boundaries, the turbulence wall treatment was that of non equilibrium, hence it is not necessary to control the y+ range of variation.

5. Swirl Generator

Swirl generator is characterized by eight- fixed vanes in the annular nozzle with a fix angle in the trailing edge, Parra et al. [15]. The definition assumed for the swirl number is the relation between the flow-averaged-azimuthal velocity and the corresponding axial velocity, see equation 5.

Table 3. Details of different set up of swirl injectors.

Design	Flat plate	Curved blade	Flat plate
Chord	50 mm	50 mm	25 mm
Swirler Angle	22º	54º	64º
Swirl number	0.14	0.74	0.95

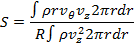
Hence different swirl numbers request different orientation for the vanes. Previous studies have verified the lack of influence of the swirler's chord on the swirl number as well as the weak influence of the design (flat plates or curved blades) on the final flow pattern. Table 3 shows the different swirler configurations presented in this paper to provide different swirl numbers.

6. Influence of Swirl Number

This section is devoted to the analysis of the flow pattern associated to low and high swirl numbers.

Figure 2 shows, for non-reactive case and swirl numbers of 0.14, 0.74 and 0.95, the contours of temperature in a longitudinal plane and the volumes of iso-value null for axial velocity. Annular jet has a temperature of 900 K whereas central jet has 300 K; hence temperature gradient suggests the mixing.

Besides, the zero axial velocity surfaces identify the position, shape and size of recirculation zones. Bearing in mind the ORZ that is formed due to the sudden expansion in the discharge of the annular nozzle [16], it has a diminishing in size while increasing the swirl number. This statement agrees with other research works [17].

Swirl number 0.74 shows an incipient IRZ while Swirl number 0.95 shows a larger IRZ. The IRZ forces the mixing; hence temperature is homogenized very close to the nozzle's discharge. This means that temperature is homogenized in more remote sections of the nozzle's discharge in the cases with low azimuthal velocity.

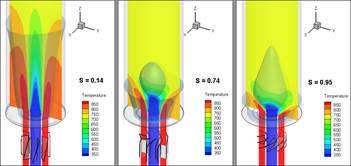
Furthermore, the shape of the IRZ in the upstream stagnation point is convex for swirl number 0.74 and concave for swirl number 0.95 increasing significant effect on heat transfer for larger swirls such it was showed in [18].

IRZ plays an essential role in homogenizing temperature. Because of the IRZ, the shear layer is deflected. The bigger the IRZ is, the thinner the shear layer is. Hence higher gradient appears. Another aspect is that the upwind stagnation point of the IRZ is approaching the discharge of the central nozzle while increasing the swirl number; hence the mixing region is small.

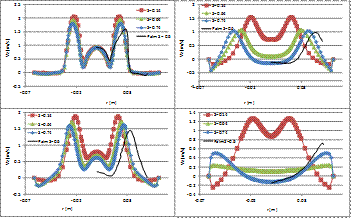
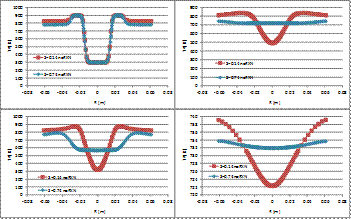
Figure 3 shows the radial profiles of axial velocity for Swirl numbers 0.14, 0.64 and 0.74 in different cross sections located at Z = 5, 25, 50 and 100 mm from the discharge of the nozzles as well as the experimental results from Palm et al. [10]. These experimental results are for a swirl of 0.6. Every section evidences the increase of momentum mixing while increasing the swirl. The sections Z = 5 mm, 25 and 50 mm show that the numerical results are less dissipative than experimental results but section Z = 100 mm section shows a good agreement with the experimental results. Negative values of the axial velocity evidence the existence of recirculation zones. It is clear the presence of ORZ in sections 25 and 50 mm for any swirl. As for the IRZ, it only appears for Swirl 0.74.

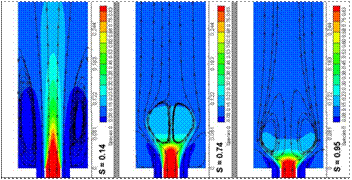
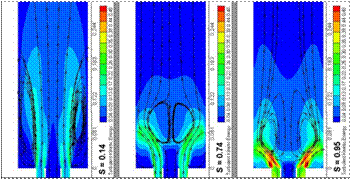
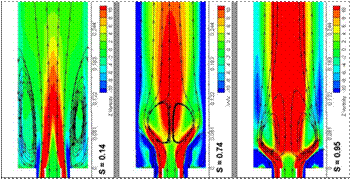
Figure 4 shows the radial profiles of temperature for Swirl numbers 0.14 and 0.74 in different cross sections located at Z = 5, 50, 100 and 300 mm from the discharge of the nozzles. Every section affected by the IRZ, Z > 5 mm and Swirl > 0.6, evidences the increase of heat transfer while increasing the swirl. Mass fraction shows similar results in the same sections. It is clear the homogenization role played by the IRZ for high swirl numbers.

Figure 5 show longitudinal contours of the passive scalar, turbulent kinetic energy and axial vorticity. The first one let identify mass mixing. Steam lines let identify the IRZ concluding the important role played in homogenizing species. Turbulent kinetic energy show maximum values on the shear layer but there is not relevant production of energy inside the IRZ. Finally, the axial vorticity is located on the annular jet because of the swirler and in the IRZ, where fluid spin as a rigid solid, with minimum deformation.

7. Conclusion

This paper studies the mixing of different swirling jets ranging from low to intermediate and high swirling numbers. Validation was provided for high swirl number.

Low swirling injectors does not promote the fluid to turn over near the centre of the chamber, resulting larger mixing zones with weak gradients. Pressure distribution for intermediate and larger swirls promote the formation of a vortex bulb near the axis of the chamber. This inner recirculation zone is responsible of deflecting the shear layer and increases the gradients near the upstream of its lead stagnation point. As a result, mixing occurs at short distance of the nozzle's discharge. Therefore it is justified the common use of swirling to burn lean mixtures that would show instable behaviour without any swirl.

Also the convex or concave shape of the recirculation point near this stagnation point is significant on the mass and heat transfer. The former appears for Swirl number 0.74 whereas the latest appears for Swirl = 0.95. Future works involve the study of reactive cases.

8. Acknowledgements

The authors thankfully acknowledge the Spanish Ministry of Science and Innovation for the financial resources in the framework of the project reference ENE2011-25468.

We acknowledge PRACE for awarding us access to resource Curie-Genci based in France at CEA and MareNostrum based in Spain at BSC. Ref. 2010PA1766.

References