Volume 3 - Year 2016 - Pages 73-85
DOI: 10.11159/jffhmt.2016.009
Numerical Solution of Incompressible Cahn-Hilliard and Navier-Stokes System with Large Density and Viscosity Ratio Using the Least-Squares Spectral Element Method
Keunsoo Park, Maria Fernandino, Carlos A. Dorao
Norwegian University of Science and Technology, Department of Energy and Process Engineering
N-7491, Trondheim, Norway 7491
keunsoo.park@ntnu.no
Abstract - There is a growing interest in numerically handling of the interface dynamics in multiphase flows with large density and viscosity ratio in several scientific and engineering applications. We present a parallel space-time implementation of a least-squares spectral element method for the incompressible Cahn-Hilliard and Navier-Stokes equations for different densities and viscosities between phases. The high-order continuity approximation is adopted to support global differentiability of problems, and by using time-stepping procedure and the element-by-element technique the effective usage of memory is resolved. Numerical experiments are conducted in order to verify the spectral/hp least-squares formulation through a convergence analysis. Besides, the efficiency of parallel computing is investigated. As general example, a falling droplet under gravity is solved by our solvers for different density and viscosity ratios, and the positive feedback between velocity field and droplet shape is investigated.
Keywords: Phase field method, Least-square method, Density ratio, Viscosity ratio, Cahn-Hilliard equation, Parallel computing
© Copyright 2016 Authors - This is an Open Access article published under the Creative Commons Attribution License terms Creative Commons Attribution License terms. Unrestricted use, distribution, and reproduction in any medium are permitted, provided the original work is properly cited.
Date Received: 2016-04-25
Date Accepted: 2016-07-20
Date Published: 2016-08-31
1. Introduction
Phase field methods [1-2] have been successfully used to simulate the flow of two or more immiscible fluids including head-on droplet collision [3-4], droplet impact on solid surface [5-6], and dripping to jetting transition [7-8]. As opposed to sharp interface methods, the phase field approach describes the interface as a transition region of physical quantities with a small but finite thickness, and it is capable of handling complex topological transition naturally without ad-hoc procedures [9]. Of the phase field models for two immiscible, incompressible and density-matched fluids, the basic model so-called Model H [10] has been widely used. It is a system of coupled Cahn-Hilliard and Navier-Stokes equations, and the thermodynamic consistency of this model was proven by Gurtin et al. [11].
There has been a growing interest in the extension of Model H for two fluids where the bulk densities and the bulk viscosities are not matched. Broadly there are two branches of models for such mixture, depending on the definition of mean velocity of two fluids. A quasi-incompressible phase field model for binary mixtures based on the mass-averaged velocity was presented by Antanovskii [12]. Lowengrub et al. [13] extended Antanovskii's model by considering the dependence of the chemical potential on the kinematic fluid pressure. However, with this definition the velocity field is non-solenoidal, and therefore the coupling of the Cahn-Hilliard and Navier-Stokes equations is mathematically much stronger, compared with Model H. For instance the pressure explicitly influences the chemical potential, and the linearization of the two equations becomes much more complicated. For these reasons, there are no discrete schemes available for the full model of Lowengrub, although there is a simplified version of the model used in numerical studies [14-15].
The formulation with the volume-averaged velocity is an alternative to Lowengrub's. This model is based on the assumption of incompressibility, and therefore the velocity field is divergence-free. The incompressibility has not only advantages with respect to numerical simulation, but also maintains the fundamental rule for diffusion, i.e., diffusive flow is controlled by the local compositions, not by the densities, imposed in the Cahn-Hilliard equation, while the total mass of the system is still conserved. Several models with the solenoidal velocity field are proposed with different expressions for the effects of density and viscosity differences (see for example [16-19]), and Aland et al. [20] compared these models for a benchmark example in terms of convergence and accuracy. In addition, various special discretization schemes are presented for these models. The advection term in the Cahn-Hilliard equation was discretized by an upwinding finite volume scheme in [16] and by the finite element method with Muramn and Resetarinera schemes in [17]. Shen et al. [18] compared the formulations with the gauge-Uzawa scheme and the pressure-stabilization scheme for large density ratios.
The objective of this study is to present the numerical scheme with the least-squares spectral element method to solve the incompressible Cahn-Hilliard and Navier-Stokes system for two-phase flow with large density and viscosity ratio. In our previous works we have presented the simulations of the Cahn-Hilliard equation and Model H using the least-squares method [21-22]. The use of the least-squares method has several advantages: (1) it converts the original non-self adjoint operator into a self-adjoin operator, leading to a symmetric positive definite discrete linear system that can be solved by well-established iterative solvers: (2) the inf-sup (or LBB) condition is naturally satisfied, so that equal-order elements can be used [23].
There are few works on two immiscible, incompressible fluids with the least-squares method. Villegas et al. [24] solved two-phase flow equation based on the level-set method with the least-squares method. Tiwari et al. [25] presented an implicit projection method based on the least-squares particle method to deal with two incompressible Navier-Stokes equations for two phases. More recently, Adler et al. [26] used the least-squares method to model Allen-Cahn-type equation.
The fourth-order Cahn-Hilliard equation can be split into two second-order partial differential equations by introducing the chemical potential as an auxiliary variable. In this work, the global differentiability of the set of these two equations and the Navier-Stokes equation is satisfied by approximating the solution with C1 Hermite polynomial functions in each element. By using higher order global differentiability in local approximations we can avoid introducing excessive auxiliary equations and auxiliary variables and achieve the improved accuracy for the same number of degrees of freedom compared to C0 approximation [27]. Surana et al. [28] showed the advantages of the higher order continuity approximation in the least-squares process. For the Cahn-Hilliard equation the use of higher order continuity approximation can result in significant improvement in the accuracy, because the solution rapidly varies over the interfacial region where a thinner interface is preferred to reproduce the correct physics. Discontinuities can result in oscillations in particular when high order polynomials are used, however, it has been demonstrated that the numerical diffusion can be completely eliminated by mesh refinement and p-enrichment in several works [23, 29].
The rest of this paper is organized as follows. In Section 2, we review the governing equations. The numerical approach is described in Section 3. Convergence analysis of our numerical formulation can be found in Section 4 and more general numerical examples are presented in Section 5. We draw conclusions in Section 6.
2. Formulation of Problem
2.1. Notations
The
formulations of the phase field method depend on the model of Helmholtz free
energy ![]() . Cahn et al. [30] proposed
a sum of the local Helmholtz energy
. Cahn et al. [30] proposed
a sum of the local Helmholtz energy ![]() and surface tension effects on the
interface as,
and surface tension effects on the
interface as,
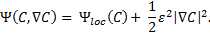
where ![]() is
the interfacial parameter, and C the concentration, defined as the
volume fraction of one phase, i.e.,
is
the interfacial parameter, and C the concentration, defined as the
volume fraction of one phase, i.e., ![]() . The local Helmholtz energy
. The local Helmholtz energy ![]() has the form of double-well to
describe immiscible two phases, and in this study it is approximated as a
fourth-order polynomial for isothermal cases [31]:
has the form of double-well to
describe immiscible two phases, and in this study it is approximated as a
fourth-order polynomial for isothermal cases [31]:
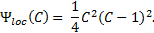
The total density of the mixture ρ and the viscosity of the mixture μ are defined as
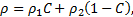
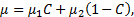
respectively,
where ![]() and
and ![]() denote the bulk density values and
denote the bulk density values and ![]() and
and ![]() are the bulk viscosities. Each fluid has its own
velocity field,
are the bulk viscosities. Each fluid has its own
velocity field, ![]() and
and ![]() , and the volume-averaged velocity
, and the volume-averaged velocity ![]() is defined as
is defined as
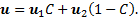
2.2. Governing equations
Following Ding et al. [16], we consider the following coupled Cahn-Hilliard and Navier-Stokes system for two immiscible, incompressible fluid flows with a given density and viscosity ratio:
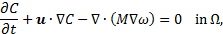
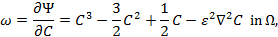
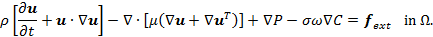
where
M is the mobility, P the pressure, ![]() the interfacial tension, and Ω
the domain. Here,
the interfacial tension, and Ω
the domain. Here, ![]() is the chemical potential for
constant temperature, which is the derivative of the free energy
is the chemical potential for
constant temperature, which is the derivative of the free energy ![]() with respect to the configuration change,
and
with respect to the configuration change,
and ![]() is the external body force expressed
as
is the external body force expressed
as ![]() , with the gravitational acceleration g.
In Eq. 6
, with the gravitational acceleration g.
In Eq. 6 ![]() is the advection term and
is the advection term and ![]() in Eq. 9 is the capillary force. Eq.
6-9 are along with the following no-penetration and no-slip boundary
conditions:
in Eq. 9 is the capillary force. Eq.
6-9 are along with the following no-penetration and no-slip boundary
conditions:
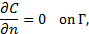
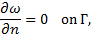
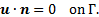
where ![]() is
the outward vector at the boundary Γ.
is
the outward vector at the boundary Γ.
In this article, the governing equations are non-dimensionalized. The dimensionless density and viscosity for a liquid-vapor mixture are defined as
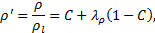
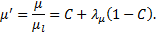
where
the density ratio and viscosity ratio are defined as the ratios of vapor
properties over the liquid one as, ![]() and
and ![]() , respectively. Other dimensionless
variables are:
, respectively. Other dimensionless
variables are:
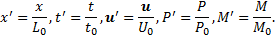
where L0, t0, U0, P0, and M0 are the reference length, time, velocity, pressure, and mobility. Dropping out the primes, Eq. 6-9 in dimensionless form can be written as
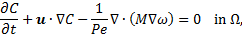
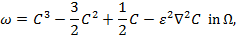
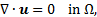
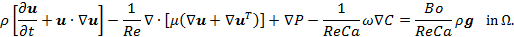
As for the dimensionless groups, Pe is the Peclet number, Re is the Reynolds number, Ca is the capillary number, and Bo is the Bond number defined as

Note that the dimensionless numbers regarding to hydrodynamics are based on the liquid values to see the effect of liquid properties.
The
study of the influence of mobility is out of the scope in this study, but two
mobilities are used depending on the problems: ![]() and
and ![]() . The first mobility is not degenerate
in the pure phases, but the second one is degenerate, i.e., zero mobility in
the pure phases. Due to this difference, with the polynomial mobility the
interface motion is determined by diffusion along the interface itself, i.e.,
surface diffusion, while the interface motion with the unity mobility is also
influenced by a diffusion process in the two bulk phases [32]. The polynomial
mobility has been introduced by Cahn et al. [33] from thermodynamic grounds.
. The first mobility is not degenerate
in the pure phases, but the second one is degenerate, i.e., zero mobility in
the pure phases. Due to this difference, with the polynomial mobility the
interface motion is determined by diffusion along the interface itself, i.e.,
surface diffusion, while the interface motion with the unity mobility is also
influenced by a diffusion process in the two bulk phases [32]. The polynomial
mobility has been introduced by Cahn et al. [33] from thermodynamic grounds.
Equilibrium
of a droplet surrounded by quiescent vapor requires the curvature of the
interface to be uniform. Otherwise, the pressure and the capillary forces at
the interface are unbalanced, giving rise to a nonzero velocity field. The
equilibrium interface profile can be found by minimizing ![]() with respect to
with respect to ![]() ,
i.e., zero chemical potential. With the double-well free energy, expressed as
Eq. 2, the equilibrium interface profile can be determined analytically as,
,
i.e., zero chemical potential. With the double-well free energy, expressed as
Eq. 2, the equilibrium interface profile can be determined analytically as,
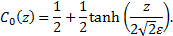
with the z-coordinate chosen along the gradient of C.
3. Numerical Methods
3.1. Least-squares method
The basic idea of the least-squares method is the minimization of the residual functional in a least-squares manner. A set of partial differential equations can be represented as
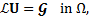
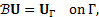
with ![]() is
a linear partial differential operator,
is
a linear partial differential operator, ![]() is a boundary operator, U is a
solution vector, and
is a boundary operator, U is a
solution vector, and ![]() and
and ![]() are corresponding source terms. We
assume that the system is well-posed and the operators
are corresponding source terms. We
assume that the system is well-posed and the operators ![]() and
and ![]() are continuous mappings from the
solution in Hilbert space
are continuous mappings from the
solution in Hilbert space ![]() onto the data in Hilbert spaces
onto the data in Hilbert spaces ![]() . The least-squares functional
corresponding to Eq. 22 can be defined as the square of the residual as,
. The least-squares functional
corresponding to Eq. 22 can be defined as the square of the residual as,
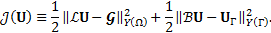
The solution is calculated from the following minimization statement based on variational analysis:
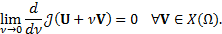
Equivalently, it is possible to write the necessary condition as:
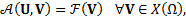
with
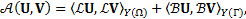
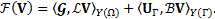
where ![]() is a symmetric, positive definite bilinear form,
and
is a symmetric, positive definite bilinear form,
and ![]() is a continuous linear form.
is a continuous linear form.
3.2. Spectral element discretization
The
computational domain Ω is divided into Ne non-overlapped
sub-domains ![]() , called spectral elements. The local
solution
, called spectral elements. The local
solution ![]() in each element
in each element ![]() is approximated as Eq. 28 by the
linear combination of a set of continuous basis functions
is approximated as Eq. 28 by the
linear combination of a set of continuous basis functions ![]()
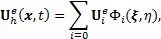
with ![]() the local coordinate of
the local coordinate of ![]() in the parent element, the unit cube
in the parent element, the unit cube ![]() , with d = dimΩ, and
, with d = dimΩ, and ![]() the
coefficients in the approximation. The global approximation
the
coefficients in the approximation. The global approximation ![]() in Ω is constructed by
connecting the local solutions, i.e.,
in Ω is constructed by
connecting the local solutions, i.e.,
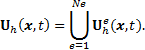
The
discretization is based on a space-time coupled formulation with the time-stepping
procedure suggested by Pontaza et al. [34]. The solution is approximated on
consecutively aligned space-time strips domains, and a strip is composed of
only one element in time, ![]() with the time
step size
with the time
step size ![]() . The initial condition of the system
is applied to the first strip, and for the subsequent strips, the final
solution from the previous strip is prescribed to the next strip as the initial
condition.
. The initial condition of the system
is applied to the first strip, and for the subsequent strips, the final
solution from the previous strip is prescribed to the next strip as the initial
condition.
3.3. Iterative method for coupling and nonlinear terms
Eq. 16-19 are the coupled Cahn-Hilliard and Navier-Stokes equations with nonlinear terms. To handle the complexities of nonlinearity and coupling, two iterative schemes are used. The Newton linearization method is used to cope with nonlinear terms, and a relaxation method is used in decoupling of the equations to assure convergence and acceleration of the iterations.
Through the Newton linearization method the nonlinear terms in Eq. 17 and Eq. 19 can be rewritten as the linear forms for the two-dimensional spatial domain, respectively:
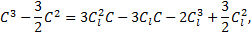
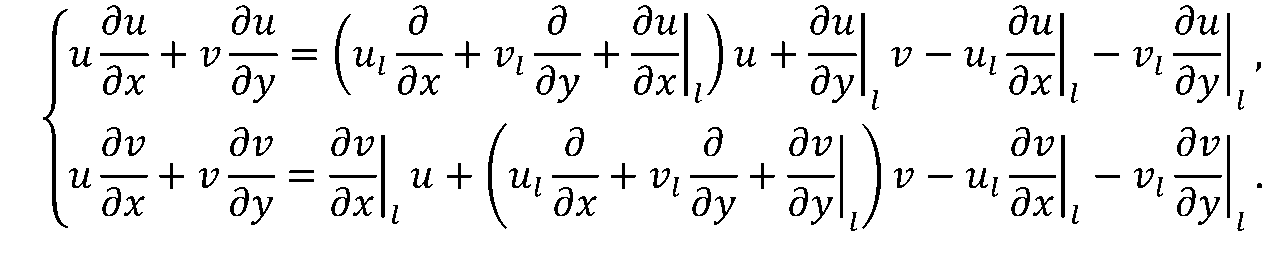
The terms with subscript l represent the values from previous iterative steps for linearization, and they are regarded as constants in the linear form.
With the linearized forms Eq. 30-31, the operators and solution vectors in Eq. 22 for the Cahn-Hilliard and Navier-Stokes equations are given in Eq. 32 and Eq. 33, respectively. The terms from previous decoupling step are denoted as subscript n.

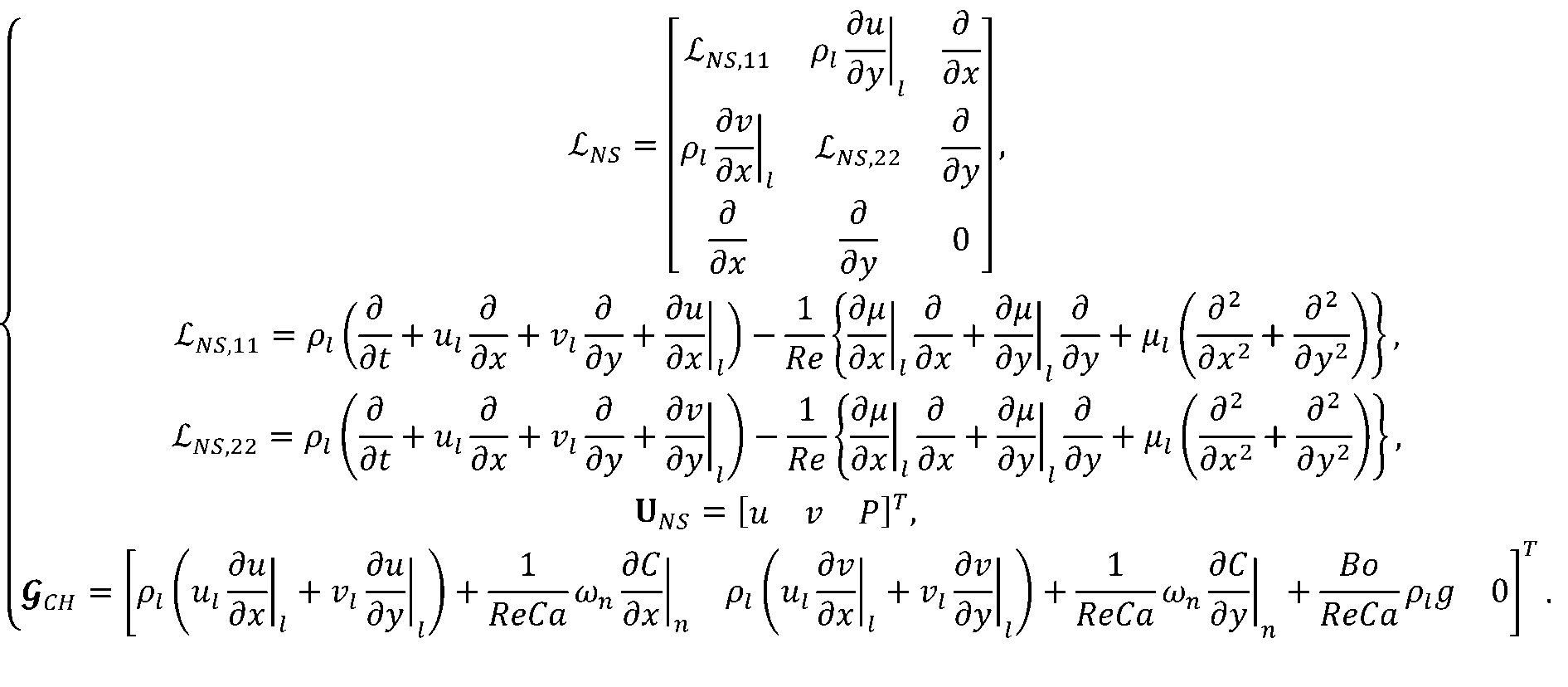
Both
nonlinear and decoupling convergences are declared when the relative norm of
the residual, i.e., ![]() , is less than 10-6, with
the residual defined as
, is less than 10-6, with
the residual defined as

3.4. C111 approximation
In
this work, for a two-dimensional space and time domain ![]() , equal order C1 p-version
hierarchical approximation functions, C111 approximation, are used
to interpolate the solution
, equal order C1 p-version
hierarchical approximation functions, C111 approximation, are used
to interpolate the solution ![]() . The solution space
. The solution space ![]() is spanned by polynomial functions of
order
is spanned by polynomial functions of
order ![]() and
and ![]() which are continuous and
differentiable for two space coordinates and the time coordinate, and their
first derivatives are continuous:
which are continuous and
differentiable for two space coordinates and the time coordinate, and their
first derivatives are continuous:
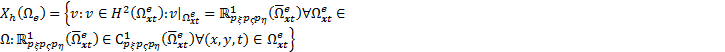
For constructing the three-dimensional basis functions, the p-version hierarchical interpolation basis functions and construction approach by Solin and Segeth [35] are used. The same basis functions and construction approach have been used in [36] for the solution of the Cahn-Hilliard equation in one-dimensional space and time domain.
The one-dimensional basis functions consist of a set of four vertex basis functions defined as the cubic Hermite polynomials. The corresponding functions in the reference domain [-1,1] are defined as
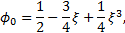
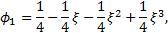
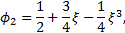
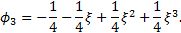
Among
these four functions, ![]() and
and ![]() contain the information of the value
of the approximation, and
contain the information of the value
of the approximation, and ![]() and
and ![]() contain the information of the
derivative at the boundary of the element. These basis functions can be
extended in a hierarchical manner for
contain the information of the
derivative at the boundary of the element. These basis functions can be
extended in a hierarchical manner for ![]() :
:
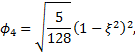
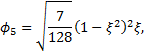
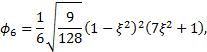
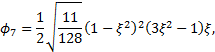
Since these shape functions vanish on the boundary of the element, they are called bubble functions.
The
three-dimensional basis functions for the space and time domains are written as
the tensor product of one-dimensional basis functions, i.e. ![]() . To simplify the numerical
manipulation, we can define the three-dimensional basis functions as
. To simplify the numerical
manipulation, we can define the three-dimensional basis functions as
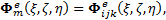
with ![]() where
where ![]() . Thus, we have
. Thus, we have ![]() basis functions
basis functions ![]() .
.
3.5. Fully discrete model
The assembling of the element matrix can be written as
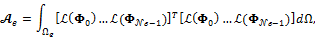
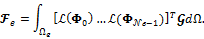
The
integral expression is numerically approximated by the Gaussian quadrature
based on the GLL-roots, and over-integration with larger number of quadrature
points Q than the expansion order p is used to improve the convergence
rate of the solution [37], ![]() .
.
We implement the conjugated gradient method with the Jacobi preconditioner to solve the system of algebraic equations, Eq. 22, in element level.
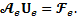
This element-by-element technique is suitable to solve a linear system possessing a symmetric positive definite matrix and well-matched with iterative methods, such as for linearization and the time-stepping procedure [38]. A Matlab code developed at our group has been used as a main setup. For parallelization of the algorithm Matlab MPI is used to allocate sub-domains to processors and communicate between processors. The governing equations in each sub-domain are solved separately, and the solution vectors are assembled in a main processor.
4. Code Verification
4.1. Convergence analysis based on the manufactured solution
In this section the presented least-squares spectral element formulation is verified with the manufactured solutions in terms of error indicator. The following manufactured solution, expressed as products of trigonometrical functions, is used:
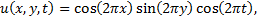
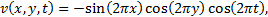
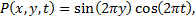
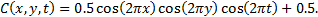
The
manufactured solution is not the analytic solution, so the residuals have to be
added to the right-hand side of the discretized equations. Initial and boundary
conditions are given by the manufactured solution; Dirichlet boundary
conditions for the velocity fields and Neumann boundary conditions for the
phase field variables are applied. In the convergence analysis, L2-norm
of difference between the approximated solution ![]() and the manufactured solution
and the manufactured solution ![]() , i.e.,
, i.e., ![]() is chosen as
error indicator and it can be written as
is chosen as
error indicator and it can be written as
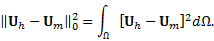
The used parameters are: ![]() , and
, and ![]() . The governing equations are solved
over a domain
. The governing equations are solved
over a domain ![]() , with
, with ![]() until 3.0 s (6 periods). The time
step size is determined through the Courant-Friedrich-Lewy (CFL) condition
until 3.0 s (6 periods). The time
step size is determined through the Courant-Friedrich-Lewy (CFL) condition
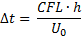
where the stable time step size is generated when CFL is around unity. A CFL spanning from 0.05 to 1.6 is used in this study with U0 of 0.5.
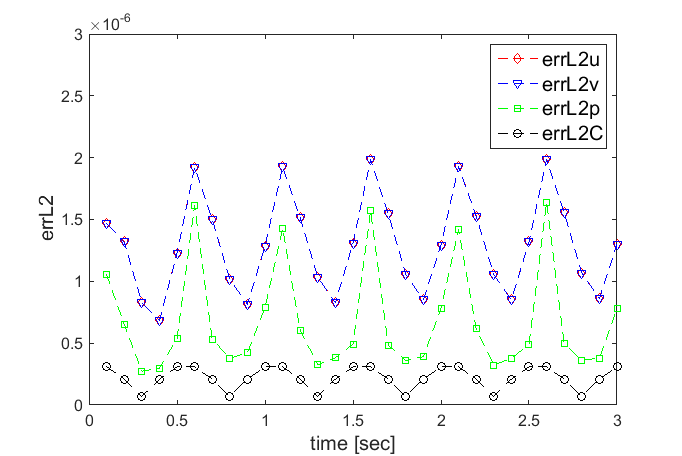
The
errors in time for ![]() and
and ![]() are presented in Figure 1. Errors
oscillate with the period of solution, and after the first period the
oscillation amplitudes become stable. It illustrates the fact that the errors
do not diverge, but just fluctuate depending on the contour of solutions.
are presented in Figure 1. Errors
oscillate with the period of solution, and after the first period the
oscillation amplitudes become stable. It illustrates the fact that the errors
do not diverge, but just fluctuate depending on the contour of solutions.
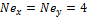 and
and 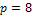 .
.The
p-refinement study ranging from ![]() to 10 and with
to 10 and with ![]() and h-refinement study of
and h-refinement study of ![]() and with
and with ![]() are conducted, and the errors at 3.0
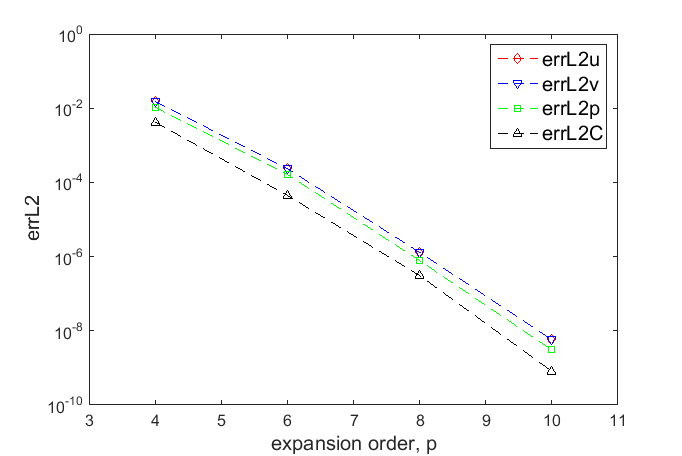
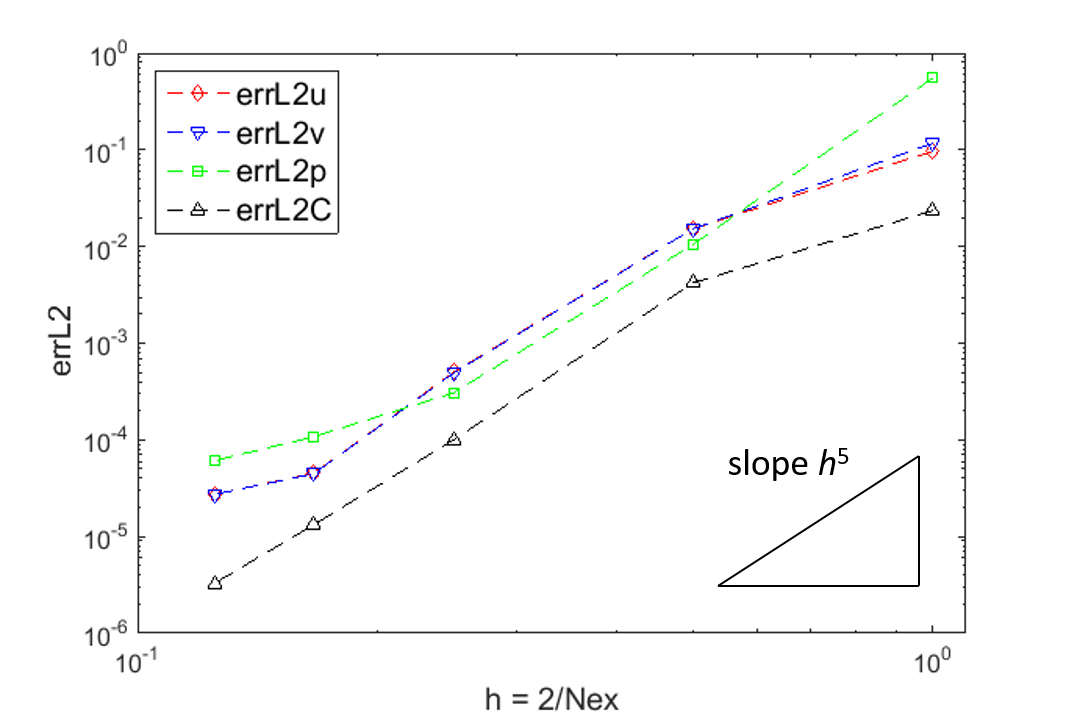
s are presented in Figure 2. The L2-errors in the p-refinement
study show exponential decay with respect to the expansion order p, as
expected for the least-squares method. The h-refinement study shows the
expected linear convergence rate with slope 5, as theoretically predicted for a
fixed order
are conducted, and the errors at 3.0
s are presented in Figure 2. The L2-errors in the p-refinement
study show exponential decay with respect to the expansion order p, as
expected for the least-squares method. The h-refinement study shows the
expected linear convergence rate with slope 5, as theoretically predicted for a
fixed order ![]() .
.
4.2. Performance of parallel computation
In
this work the parallel computation using the element-by-element technique is
implemented for a problem with a refined grid. The performance of the
parallelization is measured with the manufactured solution example. Two
parameters, the speedup ratio ![]() and the parallel efficiency
and the parallel efficiency ![]() defined as Eq. 50 and Eq. 51, are
used. The speedup ratio
defined as Eq. 50 and Eq. 51, are
used. The speedup ratio ![]() is the ratio between the elapsed time
of one processor
is the ratio between the elapsed time
of one processor ![]() and the elapsed time of np
processors
and the elapsed time of np
processors ![]() , and the parallel efficiency
, and the parallel efficiency ![]() is the speedup ratio over the number
of processors np.
is the speedup ratio over the number
of processors np.
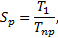
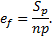
 , and h-refinement study (bottom) with
, and h-refinement study (bottom) with  .
.Figure
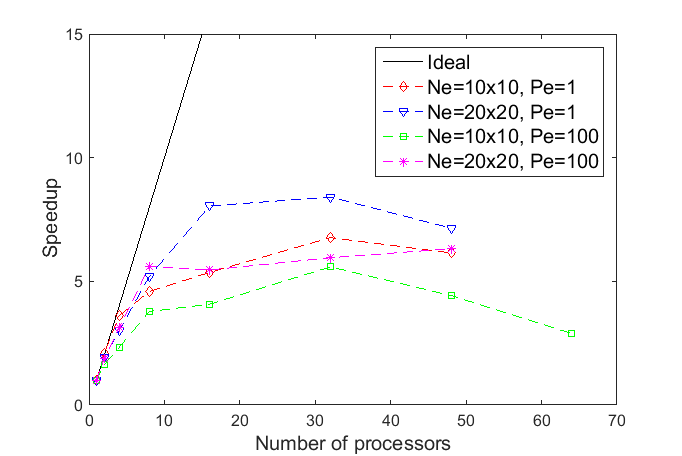
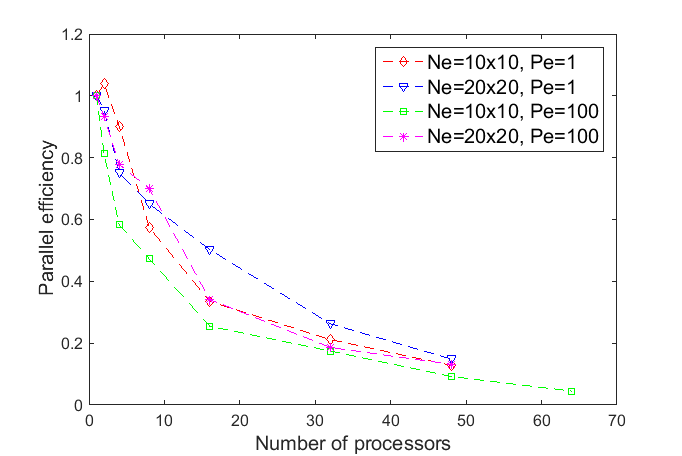
3 presents the behavior of the speedup and parallel efficiency with 1, 2, 4, 8,
16, 32, 48, and 64 processors for ![]() and
and ![]() with
with ![]() and
and ![]() elements and 4 for the expansion
order. For all simulations 32 GB of RAM were used. For all cases the
parallelization is less efficient as more processors are used because the time
required for communication becomes more dominant. Based on these results, the number
of 16 processors was adopted for further simulations in this work.
elements and 4 for the expansion
order. For all simulations 32 GB of RAM were used. For all cases the
parallelization is less efficient as more processors are used because the time
required for communication becomes more dominant. Based on these results, the number
of 16 processors was adopted for further simulations in this work.
5. Falling Droplet
We
model a falling droplet under gravity force in a vertical channel to
investigate the effects of density ratio and viscosity ratio of the two fluids.
Three parameters are used to show the effects quantitatively; center of mass ![]() , circularity c, and falling
velocity
, circularity c, and falling
velocity ![]() , which are defined as
, which are defined as
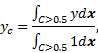
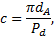
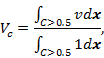
with ![]() the diameter of projected area
the diameter of projected area ![]() . Circularity is defined as a ratio
the perimeter of projected-area-equivalent circle to the perimeter of droplet. It
is assumed that the thin interface between the phases is spatially located at
. Circularity is defined as a ratio
the perimeter of projected-area-equivalent circle to the perimeter of droplet. It
is assumed that the thin interface between the phases is spatially located at ![]() .
.
The
spatial domain is chosen as a vertical channel, ![]() , and the no-penetration and no-slip boundary
conditions are applied to all boundaries. Initially a droplet with diameter D
= 0.5 is placed at
, and the no-penetration and no-slip boundary
conditions are applied to all boundaries. Initially a droplet with diameter D
= 0.5 is placed at ![]() under zero flow field, and the
initial interface condition follows the analytical solution, Eq. 21. To assure
the equilibrium state numerically as well, the simulation runs without any
external force, until L¥-norm of
difference of concentration in time is lower than
under zero flow field, and the
initial interface condition follows the analytical solution, Eq. 21. To assure
the equilibrium state numerically as well, the simulation runs without any
external force, until L¥-norm of
difference of concentration in time is lower than ![]() , i.e.,
, i.e., ![]() , and after then the gravity force
, and after then the gravity force ![]() is imposed and the characteristics of
the falling droplet are measured.
is imposed and the characteristics of
the falling droplet are measured.
We
set ![]() , and
, and ![]() for all simulations presented in this
work. The simulation runs until the droplet reaches
for all simulations presented in this
work. The simulation runs until the droplet reaches ![]() with the time step size
with the time step size ![]() , and the mesh size is taken to be
, and the mesh size is taken to be ![]() with a grid discretization of
with a grid discretization of ![]() and
and ![]() , corresponding to CFL of 0.48. The
solution is approximated by basis functions with an expansion order 4. An
example of a falling droplet with
, corresponding to CFL of 0.48. The
solution is approximated by basis functions with an expansion order 4. An
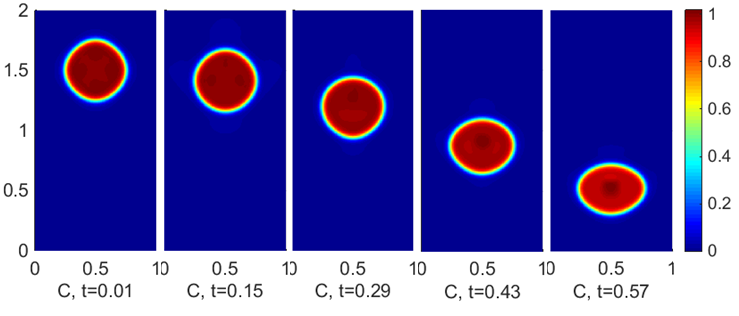
example of a falling droplet with ![]() and
and ![]() is presented in Figure 4. We observe
that the droplet falls and turns into an ellipse in time, while the interface
width and the area of the droplet are preserved.
is presented in Figure 4. We observe
that the droplet falls and turns into an ellipse in time, while the interface
width and the area of the droplet are preserved.
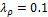 , viscosity ratio
, viscosity ratio 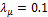 ,
, 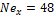 ,
, 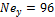 , and
, and 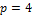 .
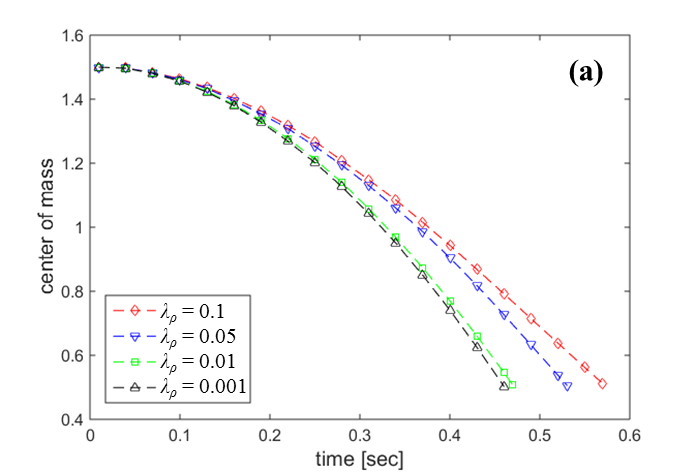
.5.1. Effects of
density ratio ![]()
Figure
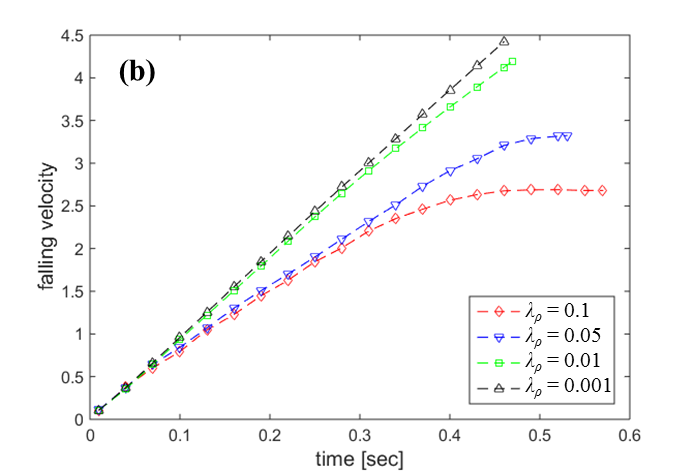
5 shows the variations of (a) center of mass and (b) falling velocity of the
droplets with four different density ratios: ![]() , and 0.001, while the bulk vapor
density is fixed at 1 and the viscosity ratio
, and 0.001, while the bulk vapor
density is fixed at 1 and the viscosity ratio ![]() is fixed at 0.1. The plateau on the
falling velocities of
is fixed at 0.1. The plateau on the
falling velocities of ![]() and 0.05 cases represent that the
droplets have reached their terminal velocities, which are around 2.6 and 3.3,
respectively. On the other hand, the falling velocities with
and 0.05 cases represent that the
droplets have reached their terminal velocities, which are around 2.6 and 3.3,
respectively. On the other hand, the falling velocities with ![]() and 0.001 show rather linearly
increasing velocities whose slopes are 9.0 and 9.6, respectively, which are
close to the value of gravity force, and it implies that the drag force for
these cases is negligible compared with buoyancy. Due to the linearity of the
falling velocity for cases
and 0.001 show rather linearly
increasing velocities whose slopes are 9.0 and 9.6, respectively, which are
close to the value of gravity force, and it implies that the drag force for
these cases is negligible compared with buoyancy. Due to the linearity of the
falling velocity for cases ![]() and 0.001, the center of mass in
time are well-fitted with the quadratic formulas,
and 0.001, the center of mass in
time are well-fitted with the quadratic formulas, ![]() and
and ![]() , respectively, while those of
, respectively, while those of ![]() and 0.05 show linear regions as the
droplets reach their terminal velocities.
and 0.05 show linear regions as the
droplets reach their terminal velocities.
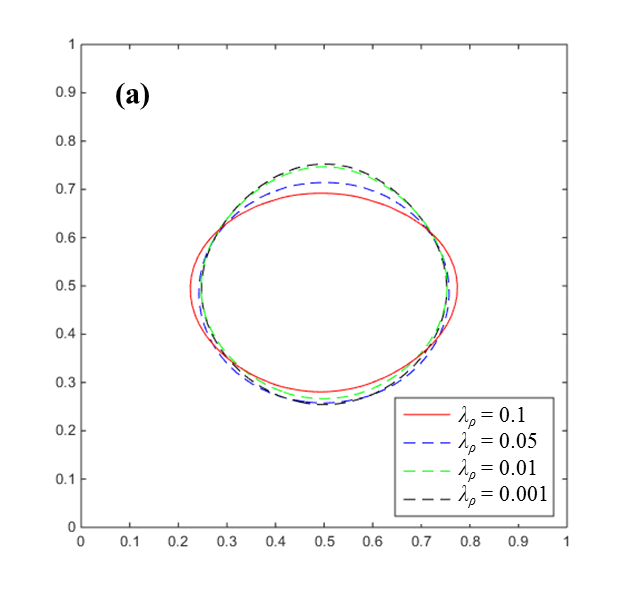
The
shapes of droplets with different ![]() around
around ![]() are presented in Figure 6(a), and
their circularities in time are given in Figure 6(b). We observe there are
insignificant differences in the droplet shapes with respect to
are presented in Figure 6(a), and
their circularities in time are given in Figure 6(b). We observe there are
insignificant differences in the droplet shapes with respect to ![]() . The buoyancy on the droplet is
approximately proportional to
. The buoyancy on the droplet is
approximately proportional to ![]() when vapor density is much smaller
than liquid density. On the other hand, the drag force onto the droplet is
proportional to
when vapor density is much smaller
than liquid density. On the other hand, the drag force onto the droplet is
proportional to ![]() because the same circularity for
different
because the same circularity for
different ![]() represents the same projected area.
Therefore it can be concluded that the force balance between buoyancy and drag
forces is mainly dependent on
represents the same projected area.
Therefore it can be concluded that the force balance between buoyancy and drag
forces is mainly dependent on ![]() , and whether the droplet reaches the
terminal velocity in a short time or not is also determined by
, and whether the droplet reaches the
terminal velocity in a short time or not is also determined by ![]() .
.
 with
with  .
.
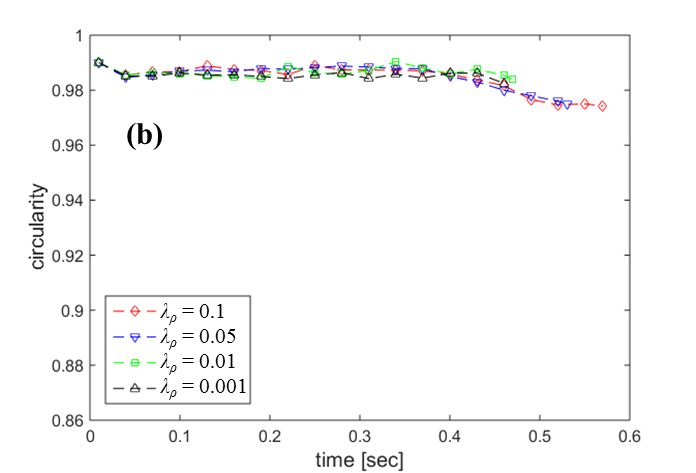
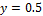 and (b) circularity in time for
different
and (b) circularity in time for
different 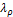 with
with 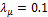 .
.5.2. Effects
of viscosity ratio ![]()
Figure
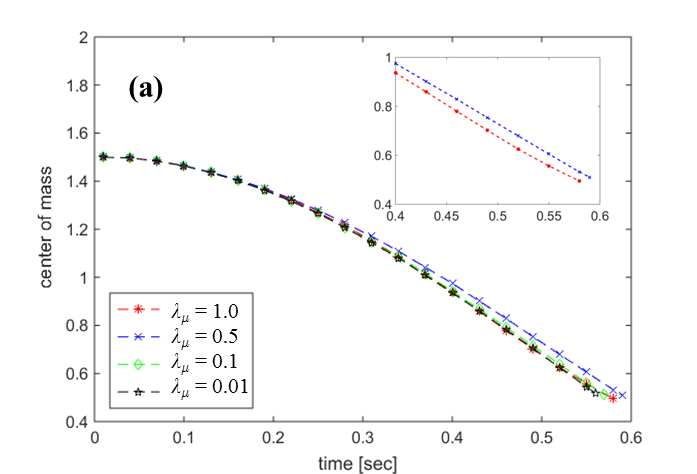
7 presents the variations of the (a) center of mass and (b) falling velocity of
the droplets with four different viscosity ratios: ![]() , 0.5, 0.1, and 0.01, while the bulk
vapor viscosity is fixed at 1 and the density ratio
, 0.5, 0.1, and 0.01, while the bulk
vapor viscosity is fixed at 1 and the density ratio ![]() is fixed at 0.1. The droplets with
is fixed at 0.1. The droplets with ![]() and 0.5 show their peak velocities at
and 0.5 show their peak velocities at ![]() and 0.5 s, respectively, while in the
other two cases the falling velocities approach their peaks. The measurements
of center of mass are in accordance with the results of falling velocity by
showing the quadratic region at the beginning and a linear region at the end.
The center of mass graph for
and 0.5 s, respectively, while in the
other two cases the falling velocities approach their peaks. The measurements
of center of mass are in accordance with the results of falling velocity by
showing the quadratic region at the beginning and a linear region at the end.
The center of mass graph for ![]() and 0.5 cases after t = 0.4 s
are enlarged and presented in Figure 7(a), and it illustrates that the slope
for
and 0.5 cases after t = 0.4 s
are enlarged and presented in Figure 7(a), and it illustrates that the slope
for ![]() has a slightly concave shape,
corresponding to its decreasing velocity after the peak.
has a slightly concave shape,
corresponding to its decreasing velocity after the peak.
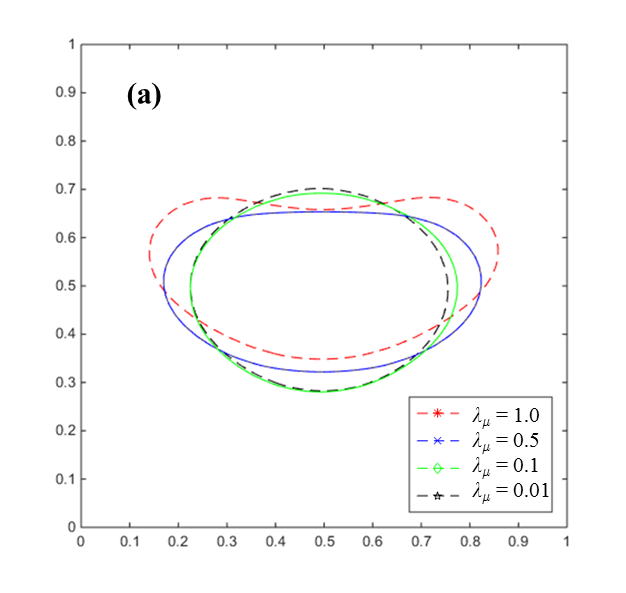
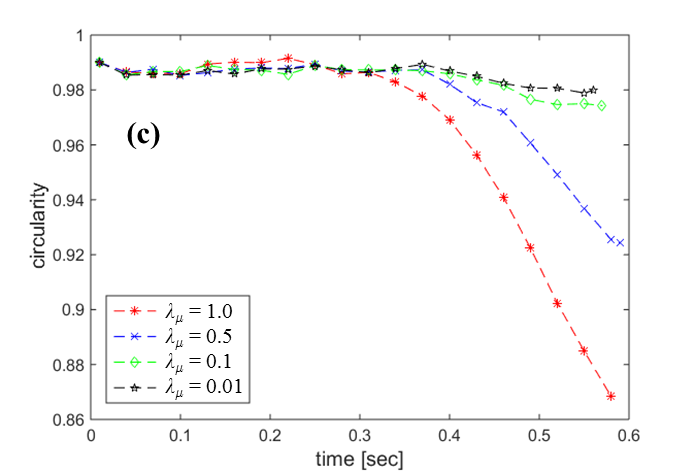
Figure 8(a) shows
the snapshot of four droplets with different ![]() when they pass around
when they pass around ![]() , and the deformation of droplets by
the location are presented in Figure 8(b), and their circularities in time are
recorded in Figure 8(c). The circular shape of droplets in
, and the deformation of droplets by
the location are presented in Figure 8(b), and their circularities in time are
recorded in Figure 8(c). The circular shape of droplets in ![]() and 0.01 cases are relatively
conserved, while in the other two cases the droplets are stretched horizontally
and even a dimple at the top is developed. With increasing
and 0.01 cases are relatively
conserved, while in the other two cases the droplets are stretched horizontally
and even a dimple at the top is developed. With increasing ![]() , the bulk liquid viscosity is lower,
and it leads to decrease of the relative strength of the surface tension to the
inertial forces. Hence, the interface can endure less pressure difference and
the droplet has a more pronounced deformation.
, the bulk liquid viscosity is lower,
and it leads to decrease of the relative strength of the surface tension to the
inertial forces. Hence, the interface can endure less pressure difference and
the droplet has a more pronounced deformation.
With
respect to the correlation of velocity and droplet shape, we can conclude that
as long as the falling droplet maintains its elliptic shape, as the cases of ![]() and 0.01, its velocity still
approaches the peak, but above this point, as the droplet is spread out or
forms a dimple, as the cases of
and 0.01, its velocity still
approaches the peak, but above this point, as the droplet is spread out or
forms a dimple, as the cases of ![]() and 0.5, the velocity starts to
drastically decrease. This difference on the evolution of velocities can be
explained by the force balance, as similar to the previous analysis. In this
example the increased drag force by
and 0.5, the velocity starts to
drastically decrease. This difference on the evolution of velocities can be
explained by the force balance, as similar to the previous analysis. In this
example the increased drag force by ![]() primarily results from larger project
area as well as higher drag coefficient, as reported in [39-42], by considering
the falling velocity and
primarily results from larger project
area as well as higher drag coefficient, as reported in [39-42], by considering
the falling velocity and ![]() are almost the same for different
are almost the same for different ![]() . The spread shape deaccelerates the
droplet, as if it plays a role as the parachute of a skydiver.
. The spread shape deaccelerates the
droplet, as if it plays a role as the parachute of a skydiver.

 with
with  .
.

 , (b) Droplet shapes in time with
different locations and viscosity ratios, and (c) circularity in time for
different
, (b) Droplet shapes in time with
different locations and viscosity ratios, and (c) circularity in time for
different 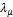 with
with 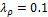 .
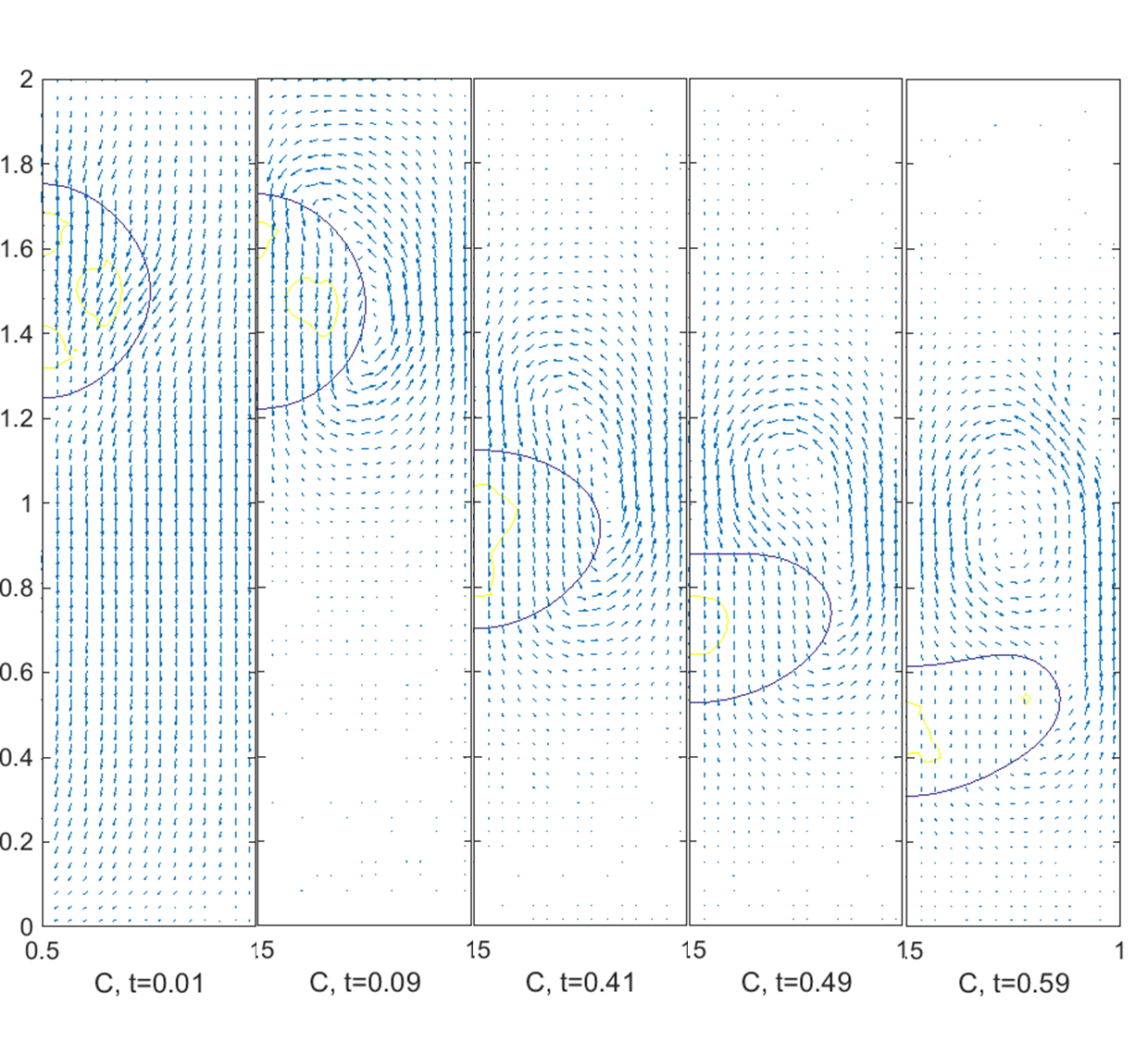
.5.3. Flow around falling droplet
Figure
9 shows the velocity field around the droplet with ![]() and
and ![]() in the right-half domain of the axis
of symmetry,
in the right-half domain of the axis
of symmetry, ![]() . As the droplet moves a doughnut-shaped
ring forms behind the droplet (from
. As the droplet moves a doughnut-shaped
ring forms behind the droplet (from ![]() ), and this ring is separated from its
tail in the form of vortex loops. Van Dyke [43] also showed from the experiment
that the vortex starts to form for Re larger than 130 and scales of the
detached eddy increase considerably with further increase in Re. Since
then, the droplet takes a shape of ellipsoid and it leads to growth of
circulating region at the rear of the droplet. With the enhanced vortex size the
velocity field stretches horizontally the fluid elements on the droplet
surface. Through this positive feedback, the droplet is further deformed. The
same result about the positive feedback was obtained in [43].
), and this ring is separated from its
tail in the form of vortex loops. Van Dyke [43] also showed from the experiment
that the vortex starts to form for Re larger than 130 and scales of the
detached eddy increase considerably with further increase in Re. Since
then, the droplet takes a shape of ellipsoid and it leads to growth of
circulating region at the rear of the droplet. With the enhanced vortex size the
velocity field stretches horizontally the fluid elements on the droplet
surface. Through this positive feedback, the droplet is further deformed. The
same result about the positive feedback was obtained in [43].
 and
and  .
.6. Conclusion
We presented the least-squares spectral element scheme for two immiscible, incompressible fluids with large density and viscosity ratio. Two-dimensional coupled Cahn-Hilliard and Navier-Stokes equation with the volume-averaged velocity was solved, and C1 cubic Hermite polynomials were used in approximating the solution. A time-stepping procedure, Newton linearization and element-by-element technique were used. The p- and h-refinement study with the manufactured solution was conducted to verify our solver, and the performance of parallelization was measured. A falling droplet was numerically handled with our solver - the effects of density and viscosity ratio on the droplet dynamics were studied, and the flow around the droplet was analyzed. According to the classification of [44], all the simulation cases in this study are sorted as 'sheet thinning' state, which is expected to have breakup with long time travel. Therefore, for future study, studies on longer simulations or higher viscosity ratio to observe sheet-like shape of droplet and ultimately break up into small pieces are recommended.
Acknowledgements
This work is supported by the Research Council of Norway (FRINATEK project 21442), Norway.
References
[1] D. Jacqmin, "Calculation of two-phase Navier-Stokes flows using phase-field modeling," J. Comput. Phys., vol. 155, no. 1, pp. 96-127, 1999. View Article
[2] J. W. Cahn and J. E. Hilliard, "Free Energy of a Nonuniform System. III. Nucleation in a Two-Component Incompressible Fluid," J. Chem. Phys., vol. 31, no. 3, pp. 688-699, 1959. View Article
[3] P. Yue, J. J. Feng, C. Liu and J. Shen, "A diffuse-interface method for simulating two-phase flows of complex fluids," J. Fluid Mech., vol. 515, pp. 293-317, 2004. View Article
[4] P. M. Dupuy, Y. Lin, M. Fernandino, H. A. Jakobsen and H. F. Svendsen, "Modelling of high pressure binary droplet collisions," Compu. Math. Appl., vol. 61, no. 12, pp. 3564-3576, 2011. View Article
[5] V. V. Khatavkar, P. D. Anderson, P. C. Duineveld and H. E. H. Meijer, "Diffuse-interface modelling of droplet impact," J. Fluid Mech., vol. 581, pp. 97-127, 2007. View Article
[6] J. Wu, C. Liu and N. Zhao, "Dynamics of falling droplets impact on a liquid film: Hybrid lattice Boltzmann simulation," Colloids Surface A, vol. 472, pp. 92-100, 2015. View Article
[7] J. Eshraghi, E. Kosari, P. Hadikhani, A. Amini, M. Ashjaee and P. Hanafizadeh, "Numerical study of surface tension effects on bubble detachment in a submerged needle," in WIT Transactions on Engineering Science, Boston, WTF Press, 2015, pp. 77-86. View Article
[8] J. Liu and X. P. Wang, "Phase field simulation of drop formation in a coflowing fluid," Int. J. Numer. Anal. Mod., vol. 12, no. 2, pp. 268-285, 2015. View Article
[9] J. Kim, "A diffuse-interface model for axisymmetric immiscible two-phase flow," Appl. Math. Comput., vol. 160, no. 2, pp. 589-606, 2005. View Article
[10] P. C. Hohenberg and B. I. Halperin, "Theory of dynamic critical phenomena," Rev. Mod. Phys., vol. 49, no. 3, p. 435, 1977. View Article
[11] M. E. Gurtin, D. Polignone and J. Viñals, "Two-phase binary fluids and immiscible fluids described by an order parameter," Math. Mod. Meth. Appl. S., vol. 6, no. 6, pp. 815-831, 1996. View Article
[12] L. K. Antanovskii, "A phase field model of capillarity," Phys. Fluids, vol. 7, no. 4, pp. 747-753, 1995. View Article
[13] J. Lowengrub and L. Truskinovsky, "Quasi-incompressible Cahn-Hilliard fluids and topological transitions," in Proceedings of the Royal Society of London A: Mathematical, Physical and Engineering Sciences, 1998. View Article
[14] H. G. Lee, J. Lowengrub and J. Goodman, "Modeling pinchoff and reconnection in a Hele-Shaw cell. I. The models and their calibration," Phys. Fluids, vol. 14, no. 2, pp. 492-513, 2002. View Article
[15] H. G. Lee, J. Lowengrub and J. Goodman, "Modeling pinchoff and reconnection in a Hele-Shaw cell. II. Analysis and simulation in the nonlinear regime," Phys. Fluids, vol. 14, no. 2, pp. 514-545, 2002. View Article
[16] H. Ding, P. D. Spelt and C. Shu, "Diffuse interface model for incompressible two-phase flows with large density ratios," J. Comput. Phys., vol. 226, no. 2, pp. 2078-2095, 2007. View Article
[17] F. Boyer, "A theoretical and numerical model for the study of incompressible mixture flows," Comput. Fluid, vol. 31, no. 1, pp. 41-68, 2002. View Article
[18] J. Shen and X. Yang, "A phase-field model and its numerical approximation for two-phase incompressible flows with different densities and viscosities," SIAM J. Sci. Comput., vol. 32, no. 3, pp. 1159-1179, 2010. View Article
[19] H. Abels, H. Garcke and G. Grün, "Thermodynamically consistent, frame indifferent diffuse interface models for incompressible two-phase flows with different densities," Math. Mod. Meth. Appl. S., vol. 22, no. 3, p. 1150013, 2012. View Article
[20] S. Aland and A. Voigt, "Benchmark computations of diffuse interface models for two-dimensional bubble dynamics," Int. J. Numer. Meth. Fl., vol. 69, no. 3, pp. 747-761, 2012. View Article
[21] K. Park, C. A. Dorao, E. M. Chiapero and M. Fernandino, "The least-squares spectral element method for the Navier-Stokes and Cahn-Hilliard equations," in Proceeding of the AJK fluid conference, Seoul, South Korea, 2015. View Article
[22] K. Park, C. A. Dorao and M. Fernandino, "Numerical solution of coupled Cahn-Hilliard and Navier-Stokes system using the least-squares spectral element method," in Proceeding of the ICNMM conference, Washington, DC, 2016.
[23] K. S. Surana and J. S. Sandhu, "Investigation of diffusion in p-version 'LSFE' and 'STLSFE' formulations," Compt. Mech., vol. 16, no. 3, pp. 151-169, 1995. View Article
[24] R. Villegas, O. Dorn, M. Moscoso and M. Kindelan, "Shape reconstruction from two-phase incompressible flow data using level sets," in Image Processing Based on Partial Differential Equations, Oslo, Springer, 2007, pp. 381-410. View Article
[25] S. Tiwari and J. Kuhnert, "Modeling of two-phase flows with surface tension by finite pointset method (FPM)," J. Comput. Appl. Math, vol. 203, no. 2, pp. 376-386, 2007. View Article
[26] J. H. Adler, J. Brannick, C. Liu, T. Manteuffel and L. Zikatanov, "First-order system least squares and the energetic variational approach for two-phase flow," J. Comput. Phys., vol. 230, no. 17, pp. 6647-6663, 2011. View Article
[27] A. Ahmadi, K. S. Surana, R. K. Maduri, A. Romkes and J. N. Reddy, "Higher order global differentiability local approximations for 2-D distorted quadrilateral elements," Int. J. Comput. Meth. Eng. Sci. Mech., vol. 10, no. 1, pp. 1-19, 2009. View Article
[28] K. S. Surana, J. N. Reddy and S. Allu, "The k-version of finite element method for initial value problems: mathematical and computational framework," Int. J. Comput. Meth. Eng. Sci. Mech., vol. 8, no. 3, pp. 123-136, 2007. View Article
[29] Á. Galvão, M. Gerristsma and B. De Maerschalck, "hp-Adaptive least squares spectral element method for hyperbolic partial differential equations," J. Comput. Appl. Math., vol. 215, no. 2, pp. 409-418, 2008. View Article
[30] J. W. Cahn and J. E. Hilliard, "Free energy of a nonuniform system. I. Interfacial free energy," J. Chem. Phys., vol. 28, no. 2, pp. 258-267, 1958. View Article
[31] W. J. Boettinger, J. A. Warren, C. Beckermann and A. Karma, "Phase-field simulation of solidification," Annu. Rev. Mater. Res., vol. 32, no. 1, pp. 163-194, 2002. View Article
[32] L. Ju, J. Zhang and Q. Du, "Fast and accurate algorithms for simulating coarsening dynamics of Cahn-Hilliard equations," Comp. Mater. Sci., vol. 108, pp. 272-282, 2015. View Article
[33] J. W. Cahn and J. E. Taylor, "Overview no. 113 surface motion by surface diffusion," Acta. Mater., vol. 42, no. 4, pp. 1045-1063, 1994. View Article
[34] J. P. Pontaza and J. N. Reddy, "Space-time coupled spectral/hp least-squares finite element formulation for the incompressible Navier-Stokes equations," J. Comput. Phys., vol. 197, no. 2, pp. 418-459, 2004. View Article
[35] P. Šolin and K. Segeth, "Towards optimal shape functions for hierarchical Hermite elements," in Proceedings of the SANM conference, Srni, Czech Republic, 2005. View Article
[36] M. Fernandino and C. Dorao, "The least squares spectral element method for the Cahn-Hilliard equation," Appl. Math. Model., vol. 35, no. 2, pp. 797-806, 2011. View Article
[37] B. De Maerschalck and M. I. Gerritsma, "Higher-order Gauss-Lobatto integration for non-linear hyperbolic equations," J. Sci. Comput., vol. 27, no. 1-3, pp. 201-214, 2006. View Article
[38] B. N. Jiang and L. A. Povinelli, "Least-squares finite element method for fluid dynamics," Comput. Method. Appl. M., vol. 81, no. 1, pp. 13-37, 1990. View Article
[39] A. R. Wadhwa, V. Magi and J. Abraham, "Transient deformation and drag of decelerating drops in axisymmetric flows," Phys. Fluids, vol. 19, no. 11, p. 113301, 2007. View Article
[40] E. Loath, "Quasi-steady shape and drag of deformable bubbles and drops," Int. J. Multiphase Flow, vol. 34, no. 6, pp. 523-546, 2008. View Article
[41] Z. G. Feng and E. E. Michaelides, "Drag coefficients of viscous spheres at intermediate and high Reynolds numbers," J. Fluids Eng, vol. 123, no. 4, pp. 841-849, 2001. View Article
[42] T. Beatus, R. H. Bar-Ziv and T. Tlusty, "The physics of 2D microfluidic droplet ensembles," Phys. Rep, vol. 516, no. 3, pp. 103-145, 2012. View Article
[43] M. Van Dyke, An album of fluid motion, Stanford, Calif.: Parabolic Press, 2012. View Article
[44] D. R. Guildenbecher, C. Lopez-Rivera and P. E. Sojka, "Secondary atomization," Experiments in Fluids, vol. 46, no. 3, pp. 371-402, 2009. View Article

