Volume 3 - Year 2016 - Pages 54-61
DOI: 10.11159/jffhmt.2016.007
Quantification of Hemodynamic Pulse Wave Velocity Based on a Thick Wall Multi-Layer Model for Blood Vessels
Jeffrey S. Lillie, Alexander S. Liberson, David A. Borkholder
Rochester Institute of Technology
James E. Gleason Building
76 Lomb Memorial Drive
Rochester, NY 14623-5604
Phone: 585-475-6067
Fax: 585-475-7710
david.borkholder@rit.edu
Abstract - Pulse wave velocity (PWV) is an important index of arterial hemodynamics, which lays the foundation for continuous, noninvasive blood pressure automated monitoring. The goal of this paper is to examine the accuracy of PWV prediction based on a traditional homogeneous structural model for thin-walled arterial segments. In reality arteries are described as composite heterogeneous hyperelastic structures, where the thickness dimension cannot be considered small compared to the cross section size. In this paper we present a hemodynamic fluid - structure interaction model accounting for the variation of geometry and material properties in a radial direction. The model is suitable to account for the highly nonlinear orthotropic material undergoing finite deformation for each layer. Numerical analysis of single and two layer arterial segments shows that a single thick layer model provides sufficient accuracy to predict PWV. The dependence of PWV on pressure for three vessels of different thicknesses is compared against a traditional thin wall model of a membrane shell interacting with an incompressible fluid. The presented thick wall model provides greater accuracy in the prediction of PWV, and will be important for blood pressure estimation based on PWV measurements.
Keywords: Pulse wave velocity, thick wall, multi-layer model noninvasive blood pressure, convective fluid phenomena, hyperelasticity, finite deformation
© Copyright 2016 Authors - This is an Open Access article published under the Creative Commons Attribution License terms Creative Commons Attribution License terms. Unrestricted use, distribution, and reproduction in any medium are permitted, provided the original work is properly cited.
Date Received: 2016-02-03
Date Accepted: 2016-03-27
Date Published: 2016-04-26
Nomenclature
|
A |
Cross sectional area (m2) |
|
u |
Axial flow velocity (m/s) |
|
p |
Transmural pressure (Pa) |
|
ρ |
Density of incompressible fluid (kg/m3) |
|
H |
Arterial wall thickness (m) |
|
|
Internal and external wall radii in a zero stress condition respectively (m) |
|
η |
Ratio of
the wall internal surface normal displacement to the radial coordinate |
|
|
Stretch ratios in a radial, circumferential and axial directions respectively |
|
|
Circumferential and radial Cauchy stress components (Pa) |
|
|
Circumferential and radial Green-Lagrange strain components |
|
A |
|
|
W |
Strain energy density function |
|
Q |
Quadratic function of the Green-Lagrange strains |
|
|
Kronecker delta: is one if the variables are equal, and zero otherwise |
|
Subscripts |
|
|
(t,z)
Superscript T |
Derivatives by time and axial coordinates
Transpose matrix or vector |
1. Introduction
Pulse wave velocity (PWV) quantification commonly serves as a highly robust prognostic parameter being used in a preventative cardiovascular therapy. Being dependent on arterial elastance, it can serve as a marker of cardiovascular risk [1]. Since it is influenced by a blood pressure (BP), the pertaining theory can lay the foundation in developing a technique for noninvasive blood pressure measurement.
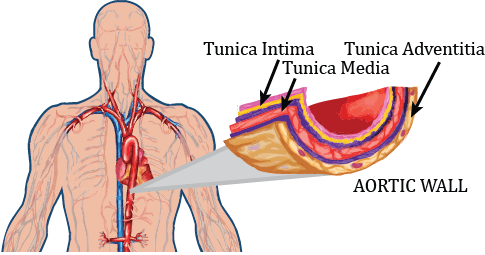
The potential of estimating arterial blood pressure based on PWV has been investigated in a number of publications considering a linearized acoustical approach (Moens-Korteweg equation), or its empirical generalization, introducing exponential presentation of the Young modulus as a function of a blood pressure (BP) [1-3]. A physically based characterization built by modeling arteries as fluid-filled compliant thin walled cylindrical membrane shells is presented in [4,5]. The present paper describes a mathematical model predicting PWV propagation with rigorous account of nonlinearities in the fluid dynamics model, blood vessel elasticity, and finite dynamic deformation of multi-layer thick wall arterial segments. This model is validated within the context of published vessel characteristics and finite element simulations, with extension to PWV and application to continuous, noninvasive blood pressure measurements. In the present work, the arterial wall is considered as a heterogeneous composite hyperelastic structure. Healthy arteries are composed of three distinct layers: the tunica intima (the innermost layer), the tunica media (the middle layer) and the tunica adventitia (the outer layer), as shown in Figure 1. We discuss a material description of each layer without thin-wall assumptions, based on a material description of an artery in a passive state originally proposed by Zhou and Fung [6]. A novel mathematical model predicting PWV is proposed accounting for nonlinear aspects of a convective fluid phenomena, hyperelastic constitutive relations, and finite deformation of a thick arterial wall. The errors introduced by the “thin” walled assumptions have been explored by Bergel [7] (replicated by [1]), based on a linear elastic model for the vessel walls undergoing small deformations. The present work extends this analysis by accounting more accurately for material properties and finite deformation in arterial hydro-elastodynamics.
2. Theory
2.1. Fluid-Structure Interaction Model
One dimensional models simulating blood flow in arteries effectively describe pulsatile flow in terms of averages across the section flow parameters. Although they are not able to provide the details of flow separation, recirculation, or shear stress analysis, they should accurately represent the overall and averaged pulsatile flow characteristics, particular PWV. Derivations of one dimensional models can be found in a number of papers, see for instance [4-5], and are not repeated here.
Conservation of mass and momentum results in the following system of one dimensional equations
For
an impermeable thick wall vessel the pressure – strain relationship is
maintained by equilibrium condition as a function ![]() , based on relevant constitutive
relations. Noting that
, based on relevant constitutive
relations. Noting that ![]() , and assuming that transmural
pressure is a smooth function of a wall normal displacement (derivative
, and assuming that transmural
pressure is a smooth function of a wall normal displacement (derivative ![]() exists at any point), the total
system of equations can be presented in the following non-conservative form
exists at any point), the total
system of equations can be presented in the following non-conservative form
where
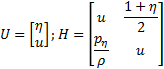
The characteristics analysis shows that the system (3) is strictly hyperbolic, with real and distinct eigenvalues. PWV is associated with the forward running wave velocity, i.e. the largest eigenvalue, hence it is identified as
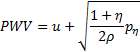
The
partial derivative ![]() indicates sensitivity of pressure
with respect to the wall normal displacement, and has a clear interpretation as
tangent (incremental) moduli in finite strain deformation. System (1), (2) is
typically closed by defining an explicit algebraic relationship between
pressure and normal displacement. For instance, in case of a small deformation
and linear elastic response of a thin walled membrane cylindrical shell
pressure relates to the circumferential strain via
indicates sensitivity of pressure
with respect to the wall normal displacement, and has a clear interpretation as
tangent (incremental) moduli in finite strain deformation. System (1), (2) is
typically closed by defining an explicit algebraic relationship between
pressure and normal displacement. For instance, in case of a small deformation
and linear elastic response of a thin walled membrane cylindrical shell
pressure relates to the circumferential strain via
so that equations (5), (6) can be transformed to the simplified form
in which ![]() is the Moens-Korteweg speed of
propagation [1]
is the Moens-Korteweg speed of
propagation [1]
Under
the assumption ![]() (linearized approach) equation (7)
converts into the Moens –Korteweg equation for the forward and backward
travelling waves. In the general case, equation (5) is supplemented by
constituent equations for a hyperelastic anisotropic arterial wall, accounting
for the finite deformation.
(linearized approach) equation (7)
converts into the Moens –Korteweg equation for the forward and backward
travelling waves. In the general case, equation (5) is supplemented by
constituent equations for a hyperelastic anisotropic arterial wall, accounting
for the finite deformation.
2.2. Mechanical framework
Consider axisymmetric case
with polar coordinate R describing material point in a load free state (Lagrangian
frame of reference), and a polar coordinate r=r(R) associated with a moving
particle (Eulerian description) – in a deformed state. Axial tethering is not
considered here, and axial strain component is neglected. The corresponding
principal stretch ratios ![]() and the Green strains
and the Green strains ![]() , are [8].
, are [8].
Numerous formulations of constitutive models for arteries have been proposed in the literature. In a comparison paper [10] it is concluded that the exponential descriptor of the passive behavior of arteries, due to Zhou-Fung, is “the best available”. According to Zhou-Fung [6] the strain energy density function for the pseudo elastic constitutive relation may be presented in the form
where c is the
material coefficient, Q is the quadratic function of the Green-Lagrange
strains ![]() and material parameters
and material parameters ![]() tensor [6]
tensor [6]
For infinitesimally small strains the exponential form of energy function is reduced to the following quadratic form, relating to the plane theory of linear anisotropic elasticity
The Cauchy – Green stress components are defined as the following [6].
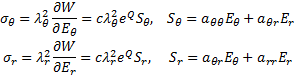
Neglecting inertia forces, the problem of an artery subjected by transmural pressure is described by solving equation of equilibrium in Eulerian frame [8]
that could be transformed to the Lagrangian coordinates using (8)
Note, that additional equation for the strains, known as the compatibility equation, follows from (8)
Or, in term of circumferential Green strain component
The boundary conditions for the internal and external radii of the artery are
Equations (8), (12), (14), (16) and the boundary conditions (17) allow us to find components of stress, strain and stretch ratios as functions of a transmural pressure, as well as incremental moduli of hyperelastic finite deformation, required by (5) to predict a wave front speed of propagation, i.e. PWV.
In a view of numerical analysis we have to derive the tangent moduli (D) by
differentiation of a stress-strain relationship (12) (![]() - Kronecker delta: is one if the variables are
equal and zero otherwise)
- Kronecker delta: is one if the variables are
equal and zero otherwise)
2.3. Continuation method for the nonlinear boundary value problem
The theory of
continuation method enables the transformation of a boundary value problem into
the initial value problem by introducing a parameter, with the following
imbedding the considered problem into the family of relating parametric
problems [9]. We introduce a load parameter ![]() and substitute
and substitute ![]() considering continuous successive load of the
vessel by internal pressure from zero to a nominal value. Assume that solution
of (8-17) depends continuously on this parameter and is differentiable with
respect to this parameter. Starting from the known answer for a certain value
of the parameter (
considering continuous successive load of the
vessel by internal pressure from zero to a nominal value. Assume that solution
of (8-17) depends continuously on this parameter and is differentiable with
respect to this parameter. Starting from the known answer for a certain value
of the parameter (![]() in the present case), the solution of the
equation for other values of the parameter may be obtained by integrating the
rate of change of the solution with respect to the parameter.
in the present case), the solution of the
equation for other values of the parameter may be obtained by integrating the
rate of change of the solution with respect to the parameter.
Differentiating
constituent equations (12) by continuation parameter (the dot above means partial
derivative by ![]() ), yields
), yields
To
solve the problem numerically, we select the vector variable ![]() as the primary variable in our model, since it
preserves continuity for the multilayered structure with discontinuous
mechanical properties. The rate of “discontinuous” variables
as the primary variable in our model, since it
preserves continuity for the multilayered structure with discontinuous
mechanical properties. The rate of “discontinuous” variables ![]() follows from (19) accordingly
follows from (19) accordingly
To
differentiate equation (14) by ![]() , expand logarithm of the algebraic part
, expand logarithm of the algebraic part ![]()
and take derivatives of both sides
Similar procedure, applied to the compatibility equation (16) yields
Now equations (22), (23) could be presented in a matrix form
in which
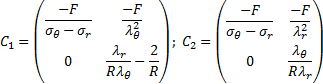
Substituting (20) in Eq.(24) we arrive at the final differential equation
with
the boundary conditions, obtained by differentiation of the boundary conditions
(17) (note that pressure in (17) is being multiplied by τ, and ![]() )
)
I
The initial parameter method presumes the solution of the linear boundary value problem (26) to be represented in the form
Here
the vector functions ![]() are independent solutions of equation 26 with
the following initial conditions
are independent solutions of equation 26 with
the following initial conditions
and μ is an unknown constant determined from the second boundary condition (27)
Once ![]() is known at
is known at ![]() , then vector
, then vector ![]() of
continuous variables and vector
of
continuous variables and vector ![]() of discontinuous functions could be calculated
by integrating the relating rate of change
of discontinuous functions could be calculated
by integrating the relating rate of change
The
above process continues to obtain solutions for τ=1. The pressure
vs. normal displacement ![]() , is tracked at
, is tracked at ![]() for each level of successively increasing load
to create incremental moduli
for each level of successively increasing load
to create incremental moduli ![]() function, required by equation (5) to predict a
wave front speed of propagation, i.e. PWV.
function, required by equation (5) to predict a
wave front speed of propagation, i.e. PWV.
3. Results and Discussion
To
validate the algorithm the numerical investigation of an inflated rabbit
carotid arterial segment is presented and compared to the results based on a
finite element analysis, obtained by Holzaphel et al. [10]. We use the rabbit
arterial data presented by Chuong and Fung [11]: c=26.95kPa; ![]() ,
, ![]() ,
, ![]() , R1=0.71 mm, R2=1.1
mm (from experiment number 71). Figure 2a shows the predicted mechanical
response of the considered artery. Squares relate to the finite element
analysis [10] and are in a good agreement with the results based on our present
single layer thick wall model. The derivative
, R1=0.71 mm, R2=1.1
mm (from experiment number 71). Figure 2a shows the predicted mechanical
response of the considered artery. Squares relate to the finite element
analysis [10] and are in a good agreement with the results based on our present
single layer thick wall model. The derivative ![]() of pressure by radial displacement
of an internal surface, i.e. hyperelastic incremental moduli, presented in
Figure 2b, is a primary factor affecting PWV in a cylinder filled with a moving
fluid according to equation (5). At diastolic pressure when flow is close to
zero, PWV is dominated by the physical anisotropic properties of the aorta. At
systolic pressure the pulse wave velocity is also affected by flow velocity
which may be approximated as 20-25% of PWV according to [15]. The insight from
equation (5) enables the PWV measure to be used for prediction of both SBP and
DBP.
of pressure by radial displacement
of an internal surface, i.e. hyperelastic incremental moduli, presented in
Figure 2b, is a primary factor affecting PWV in a cylinder filled with a moving
fluid according to equation (5). At diastolic pressure when flow is close to
zero, PWV is dominated by the physical anisotropic properties of the aorta. At
systolic pressure the pulse wave velocity is also affected by flow velocity
which may be approximated as 20-25% of PWV according to [15]. The insight from
equation (5) enables the PWV measure to be used for prediction of both SBP and
DBP.
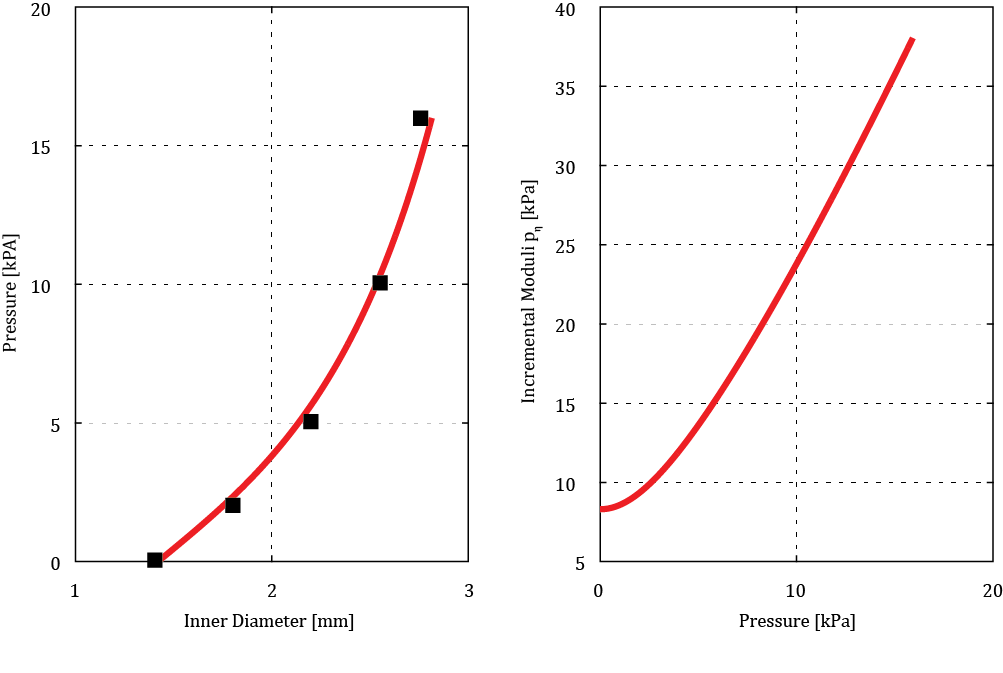
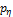 of the hyperelastic artery, i.e.
derivative of a pressure by the radial displacement
of the hyperelastic artery, i.e.
derivative of a pressure by the radial displacement 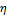 .
.A single layer thick wall model with homogeneous mechanical properties does not account for the distinct mechanical response of the separate layers (intima, media, adventitia). Since the intima contributes negligible mechanical strength [10], a two- layer model, incorporating media and adventitia only, is analyzed. We assume, following [10, 12], that media occupies approximately 0.6 of the arterial wall thickness. Experimental tests indicate that media is about 10 times stiffer that adventitia [12, 13], which allows to scale accordingly material properties tensor A.
Figure 3 depicts predicted mechanical response of the considered artery, calculated based on a single layer thick wall model (dash lines) and two-layers thick wall model (solid lines). The circumferential Cauchy stress is plotted in Figure 3a, normal displacement in Figure 3b, and radial component of Green strain in Figure 3c, all against the radial coordinate. The abrupt change of mechanical properties at the boundary between media and adventitia results in a sharp discontinuity of circumferential stress and radial strain components. Radial displacement is a continuous function, deviating slightly from the single layer counterpart as shown in Figure 3b. In the proximity of internal cylindrical surface distributions of all parameters calculated by both models (1 layer, 2 layers) are identical. Since PWV is determined by the local wall stiffness, relating to the internal cylindrical surface, the latter justifies application of the single thick layer model to the PWV based blood pressure predictions.
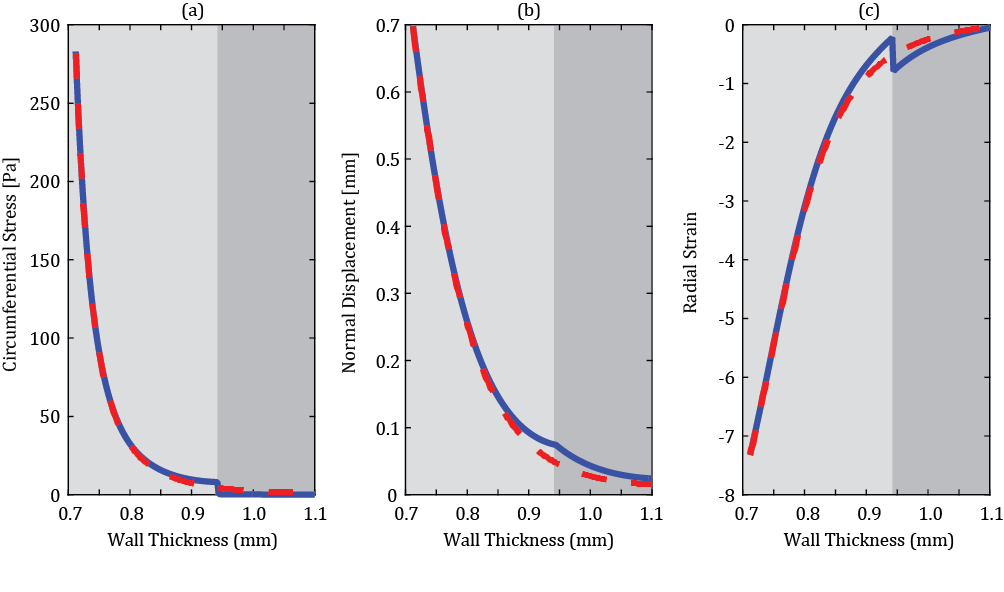
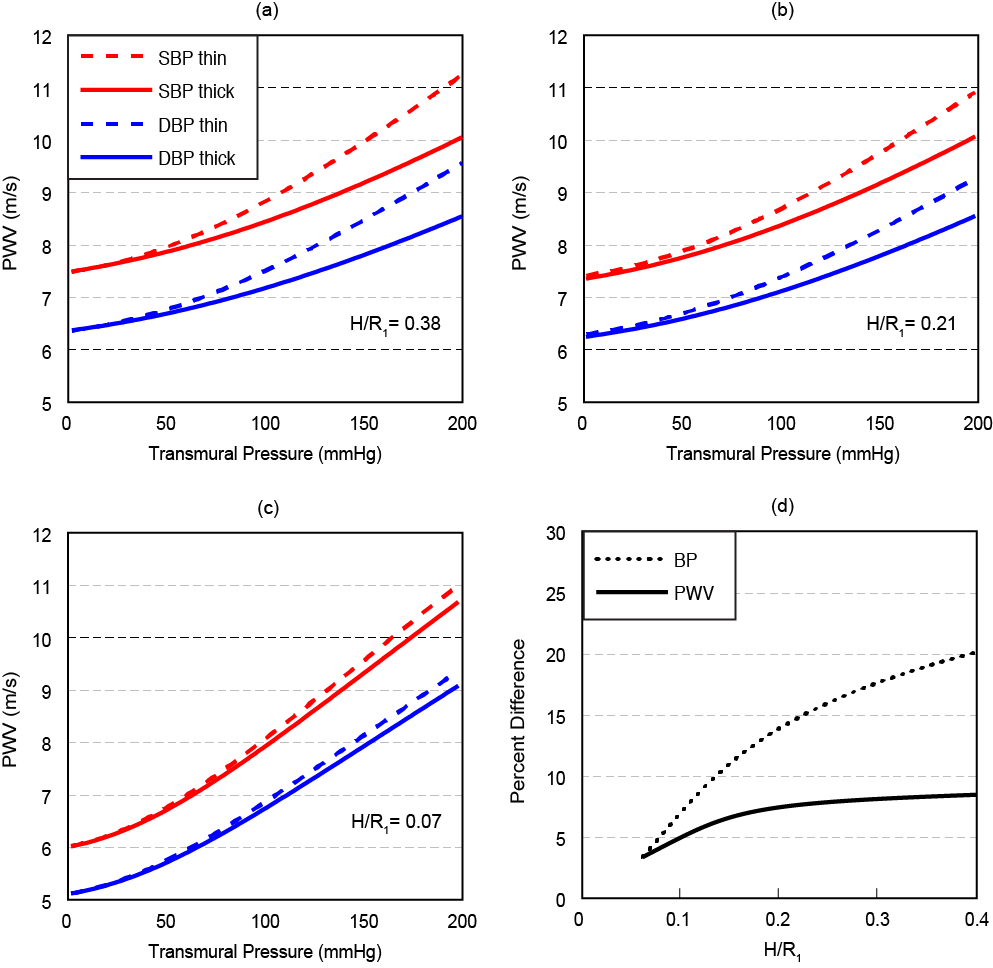
Figure 4 depicts the dependence of PWV on pressure for the systole phase (marked as “SBP”) and a diastole phase (marked as “DBP”) for three vessels of different thicknesses of a human aorta. The anisotropic material constants for a human aorta with an outer radius of 14.5mm are used from Fung et al. [14]. The inner radius is then set based on the three wall thickness considered in Figure 4. Following [15] we assume here that the flow velocity u=0 for the diastole phase, and is equal to 20% of PWV for the systole phase. All results have been compared with the simplified thin walled model of a membrane shell interacting with an incompressible fluid [5].
The analysis presented in Figure 4 considers normal wall thicknesses less than 4mm [16] across a range of transmural blood pressures. To explore inaccuracies induced by use of the less complex thin wall model, error in both PWV and blood pressure were calculated for a blood pressure of SBP/DBP = 150/95 mmHg representing the median of stage 1 hypertension [17]. The single layer thick wall model improves PWV accuracy by 4.0-8.4% across a range of normal wall thickness. One of the goals for the model is PWV-based blood pressure prediction, where the thick wall model offers an improvement of 3.3-19.4%. Accuracy improvements are highly dependent on the relative dimensions of wall thickness to arterial radius. As the ratio of H/R1 approaches zero, the error of PWV prediction approaches zero, showing an asymptotic accuracy as an order of wall thickness to internal radius ratio.
4. Conclusion
In this paper we first emphasize the importance of predicting PWV of thick wall arteries based on a three-dimensional anisotropic material description. Age related thickening of the wall, or cardiovascular diseases may cause notable change of a vessel wall thickness [1]. The model employed above is based on a Y.C. Fung phenomenological approach in which the macroscopic nature of the anisotropic biological material is modeled. A novel mathematical model predicting PWV propagation with rigorous account of nonlinearities in the fluid dynamics model, blood vessel elasticity, and finite deformation of multi-layer thick wall arterial segments was studied. It was found that the account for the multilayer model affects distribution of local parameters in the proximity of the external layer (adventitia), and does not affect stiffness related to the internal layer. The latter means that the single thick layer model is sufficient to predict PWV of an arterial segment. For a hypertensive subject, the three dimensional thick wall model provides improved accuracy up to 8.4% in PWV prediction over its thin wall counterpart. This translates to nearly 20% improvement in blood pressure prediction based on a PWV measure.
5. Acknowledgements
This research was supported by a grant from Google.
References
[1] W. Nichols, M. O'Rourke and C. Vlachopoulos, McDonald's Blood Flow in Arteries, Sixth Edition: Theoretical, Experimental and Clinical Principles, CRC Press, 2011. View Article
[2] W. Chen, T. Kobayashi, S. Ichikawa, Y. Takeuchi and T. Togawa, "Continuous estimation of systolic blood pressure using the pulse arrival time and intermittent calibration," Med Biol Eng Comput, vol. 38, pp. 569-574, 2000. View Article
[3] Y. Chen, W. Changyun, T. Guocai, B. Min and G. Li, "Continuous and Noninvasive Blood Pressure Measurement: A Novel Modeling Methodology of the Relationship Between Blood Pressure and Pulse Wave Velocity," Ann. Biomed. Eng, vol. 37, no. 11, pp. 2222-2233, 2009. View Article
[4] A. Liberson, J. S. Lillie and D. A. Borkholder, "Numerical Solution for the Boussinesq Type Models with Application to Arterial Flow," JFFHMT, vol. 1, pp. 9-15, 2014. View Article
[5] J. S. Lillie, A. S. Liberson, D. Mix, K. Schwartz, A. Chandra, D. B. Phillips, S. W. Day and D. A. Borkholder, "Pulse wave velocity prediction and compliance assessment in elastic arterial segments," Cardiovasc Eng Tech, vol. 6, pp. 49-58, 2014. View Article
[6] J. Zhou and Y. C. Fung, "The degree of nonlinearity and anisotropy of blood vessel elasticity," Proceedings of the National Academy of Sciences, vol. 94, pp. 14255-14260, 1997. View Article
[7] D. H. Bergel, "The dynamic elastic properties of the arterial wall," Journal of Physiology, vol. 156, pp. 458-469, 1961. View Article
[8] J. D. Humphrey, Cardiovascular solid mechanics. Cells, tissues, and organs, New York: Springer, 2002. View Article
[9] E. I. Grigolyuk and V. I. Shalashilin, Problems of nonlinear deformation: The continuation method applied to nonlinear problems in solid mechanics, Springer: Netherlands, 2011. View Article
[10] G. A. Holzapfel, T. Gasser and R. W. Ogden, "Comparison of Multi-Layer Structural Model for Arterial Walls with a Fung-Type Model, and Issues of Material Stability," Trans of ASME, vol. 126, 2004. View Article
[11] C. J. Chuong and Y. C. Fung, "Three dimensional stress distribution in arteries," J. Biomech. Eng., vol. 105, pp. 268-274, 1983. View Article
[12] C. A. Schulze-Bauer and G. A. Holzaphel, "Determination of constitutive Equations for human arteries from clinical data," J. Biomech., vol. 36, pp. 185-189, 2003. View Article
[13] Q. Yu, J. Zhou and Y. C. Fung, "Neutral axis location in bending and Young's modulus of different layers of arterial wall," AM Jo. Physiol., vol. 265, pp. 301-312, 1993. View Article
[14] J. Zhou and Y. C. Fung, "The degree of nonlinearity and anisotropy of blood vessel elasticity," Proceedings of the National Academy of Sciences, vol. 94, pp. 14255-14260, 1997. View Article
[15] T. J. Pedley, The Fluid Mechanics of Large Blood Vessels, Cambridge: Cambridge University Press, 2008. View Article
[16] R. Erbel and H. Eggebrecht, "Aortic Dimensions and the Risk of Disection," Heart, vol. 92, pp. 137-142, 2006. View Article
[17] G. Mancia et al., "2013 ESH/ESC Guidelines for the management of arterial hypertension," J. Hypertens, vol. 31, pp. 1281-1357, 2013. View Article

